機械臂初始構型對航天器姿態干擾力矩的影響研究

尹旺 王翔

(北京空間飛行器總體設計部，北京 100094)

由于空間機械臂能代替航天員在復雜的太空環境中方便可靠地執行一系列任務，因此世界各航天大國陸續開展了對空間機械臂的研制，隨著中國空間站任務的迫切需求，我國也開展了空間機械臂的研制工作[1]。

為保持無線通信通暢和保持對地姿態，航天器通常情況下有定向穩定要求。由于機械臂和基座之間存在動力學耦合效應，因此空間機械臂在運動時對航天器產生的基座反力會成為姿態擾動力，一方面反作用飛輪的控制力矩有上限，另一方面持續的姿態擾動可能會引起反作用飛輪的飽和，飛輪飽和后需要姿控發動機進行噴氣卸載，而發動機的控制力矩較大，為避免關節受到損壞，因此在噴氣過程中要求機械臂處于停控狀態，這勢必會增長機械臂的任務時長，這也是減少反力、減少擾動的意義。于是人們希望通過軌跡規劃的方式使機械臂在完成規定操作的同時對平臺產生的反作用最小，多數研究者都是在關節空間對機械臂的路徑進行規劃[2-5]，雖然方法的有效性得到了驗證，但是此類方法只適用于空間點到點的任務情景。當機械臂末端需要進行直線或圓弧軌跡跟蹤時，應在笛卡爾空間對機械臂的路徑進行規劃。目前機械臂在笛卡爾空間的軌跡規劃主要還是基于速度級的逆運動學，文獻[6]利用機械臂的冗余度，對關節力矩和操作靈活性進行了綜合優化，文獻[7]基于粒子群算法對冗余機械臂的自運動項進行了優化，從而使關節的驅動力矩能耗達到最優，但是自運動項的優化能力有限，并不能充分發揮冗余機械臂的優勢。

基于速度級逆運動學得到機械臂各關節速度之后，需要對關節角速度進行數值積分才能得到各關節的角位移，而進行數值積分的前提是需要給定七個關節的初始角度值，七關節的初始角也稱為機械臂的初始構型，由于七自由度機械臂存在冗余性，非奇異狀態下的機械臂有無數多種構型[8]。當機械臂末端需要沿著某一條路徑進行運行時，基于不同的初始構型進行軌跡規劃，航天器平臺受到的反作用也大小不一。因此，針對任何一種任務需求，本文期望通過對比分析得出機械臂最優的初始構型，動作之前，將機械臂調整為最優構型，能大大減小其在運行過程中對航天器產生的姿態干擾，同時使機械臂的操作效果更好。

1 七自由度機械臂模型的建立

機械臂的運動狀態依賴于軌跡規劃時初始構型的選擇，所以機械臂運動產生的反力也與初始構型密切相關。因此，建立七自由度機械臂運動學及動力學模型是后續分析研究的理論基礎，得到機械臂的運動學及動力學模型后，即可揭示機械臂在運動過程中對平臺產生的反作用與機械臂初始構型之間的關系，基于此，尋求使基座反作用達到最小的初始構型。

1.1 正運動學建模

根據Denavit和Hartenberg[9]提出的方法(D-H參數法)建立七自由度機械臂的坐標系及正運動學方程，機械臂的基坐標系{0}和各連桿的固連坐標系{i}如圖1所示(i= 1, 2, …，7)，其中，各坐標系的z軸與關節軸共線，x軸與連桿的公垂線重合，y軸根據右手法則確定。

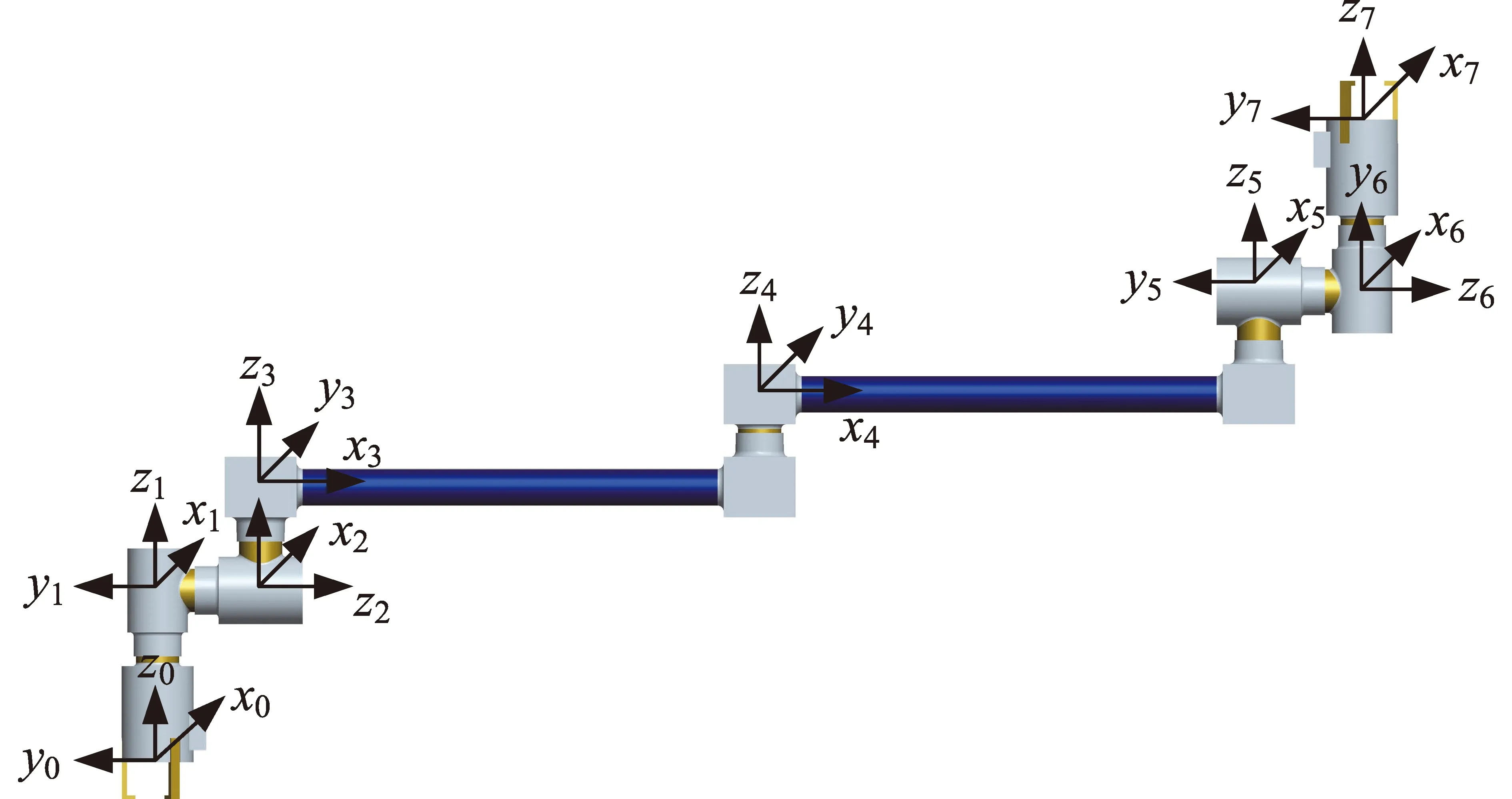
圖1 空間機械臂運動學模型Fig.1 Kinematic model of space manipulator

由D-H參數法知：4個參數可唯一確定相鄰連桿之間的變換通式，七自由度機械臂的D-H參數如表1所示。其中，li是從zi到zi+1沿xi測量的距離，代表著連桿i的長度；αi是從zi到zi+1繞xi旋轉的角度，代表連桿i的扭角；di是從xi-1到xi沿zi測量的距離，表示相鄰兩連桿之間的偏置；θi是從xi-1到xi繞zi旋轉的角度，表示相鄰兩連桿之間的轉角。

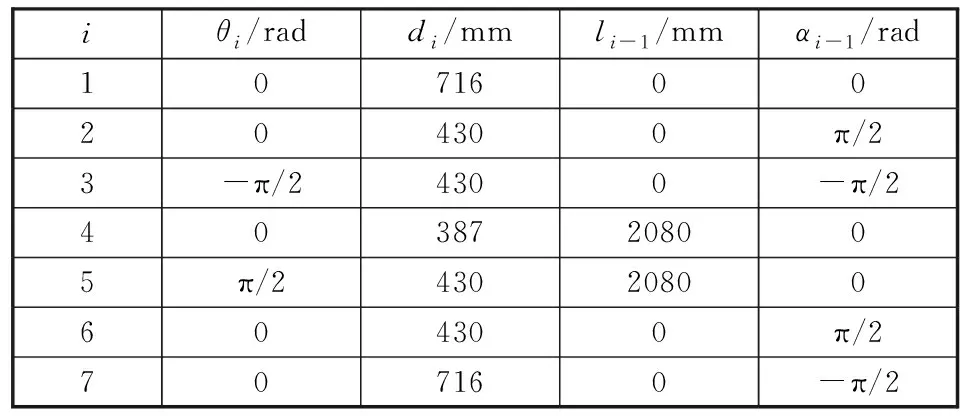
表1 七自由度機械臂的D-H參數Table 1 D-H parameters of 7-DOF manipulator

(1)

式(1)即為機械臂系統的運動學方程，表示機械臂末端相對基座的位姿與機械臂七個關節角變量θ1，θ2，…，θ7之間的關系，機械臂末端位姿可由七個關節角唯一確定。

1.2 逆運動學建模

速度級逆運動學是根據機械臂末端的廣義速度求解關節空間的角速度，而機械臂的雅克比矩陣可以將關節空間的速度線性映射到末端的操作速度

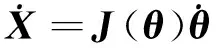
(2)

七自由度冗余機械臂在操作空間有無窮多個逆解，由矩陣理論知式(2)的逆解為

(3)

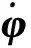
J+=JT(JJT+λ2I)-1

(4)

變阻尼系數λ為

(5)

式中：λ0稱為最大阻尼系數；σ為雅克比矩陣的最小奇異值，σ0為最小奇異邊界值。

位置級逆運動學是根據機械臂末端位姿求對應的各個關節角，本文通過關節角參數化方法求偏置式七自由度機械臂逆運動學，給定關節1的角度值，可以獲得8組逆解，由于本文和文獻[8]中機械臂的初始構型有差異，對于同一末端位姿，本文和文獻[8]中逆解之間的關系為

(6)

1.3 動力學建模

保持坐標軸方向不變，將圖1中坐標系平移到各連桿的質心處即可得到機械臂系統的質心坐標系，根據多體系統運動學理論[10]求各連桿的絕對角速度和角加速度分別為

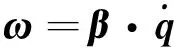
(7)

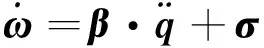
(8)

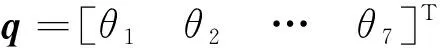
β=-(pT)T

(9)

σ=-TTh

(10)

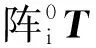
(11)

機械臂系統各連桿的質心速度和加速度可表示為

(12)

(13)

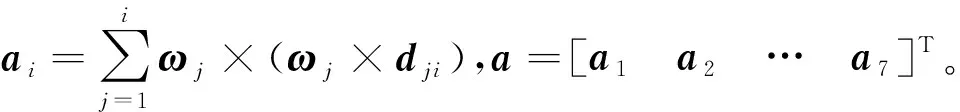
根據式(9)～式(13)求得的角速度、角加速度、質心速度和質心加速度矢量都是在基坐標系中表示的，需要通過相應的變換矩陣將其轉換到自身坐標系下。

根據牛頓-歐拉方程得到各連桿在運動過程中產生的慣性力和慣性力矩分別為

(15)

式中：mi和ciIi為機械臂系統第i個連桿的質量和相對質心的慣性張量。遞推(i:7→1)得到七自由度機械臂的逆動力學方程為

(17)

式中：ifi和ini分別為連桿i-1對連桿i的力和力矩在連桿坐標系{i}中的表示，irci表示連桿i的質心在自身坐標系下的位置矢量，-0f1和-0n1表示機械臂對航天器平臺的反作用力和力矩，當機械臂末端空載時，i+1fi+1=i+1ni+1=0。

2 基座反作用求解程序

當機械臂的末端要求按照預先設定好的路徑進行運動時，需要采用笛卡爾空間的軌跡規劃方法，為保證機械臂運行過程中的連續性和平穩性，末端速度采用基本的梯形速度曲線進行規劃。首先基于不同的初始構型規劃出各關節相應的運動狀態，然后根據各關節的運動狀態求解基座所受的反作用力矩，分析比較得出機械臂的最優初始構型，具體的算法實現過程如圖2所示。

圖2 機械臂基座反作用求解過程Fig.2 Process of solving the base reaction of manipulator

3 仿真分析

3.1 參數設置

假設機械臂末端由起點(-2,-2,2)到終點(-1.5,-1,1)做直線運動(相對于基坐標系{0})，同時運動過程中機械臂的姿態始終保持不變，仿真時長為11.5 s，共575步。運行過程中機械臂末端在基座坐標系下的姿態矩陣為

(18)

式中：R0和Rd分別為起始時刻和結束時刻的姿態矩陣。

七自由度機械臂的質量特性參數參見文獻[5]，本文針對負載為0 kg、300 kg和3000 kg的3種不同工況，研究機械臂在不同的初始構型下沿著直線運動對基座產生的反作用大小，假設將機械臂末端的負載視為附加在連桿7質心處的質量塊，且不考慮轉動慣量的影響。由上文知機械臂的初始構型與關節角1的選取密切相關，當關節角1給定時能求出八組逆解。采用枚舉法令關節角1在0～2π之間取值，間隔為0.1 rad，因此能夠得到512組計算結果。此處以基座反作用力矩(3個方向的合成)的最大值作為評價反作用大小的標準，即

(19)

3.2 結果分析

對于末端負載300 kg的工況，按以上程序計算所有初始構型下機械臂產生的反作用力矩，對512組計算結果對比分析發現：當機械臂的初始構型為[-0.48 -0.07 -2.55 1.35 -3.03 4.68 -3.20]T時，對基座產生的反作用峰值力矩達到最大為39.74 Nm，將此構型記為構型1，基于構型1進行直線路徑規劃時各關節的角位移和角速度如圖3所示。

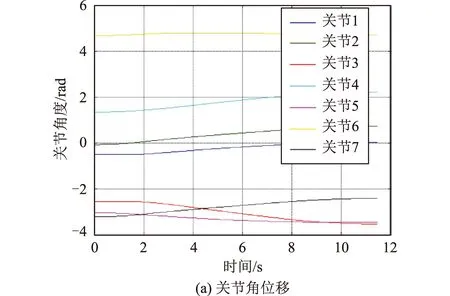
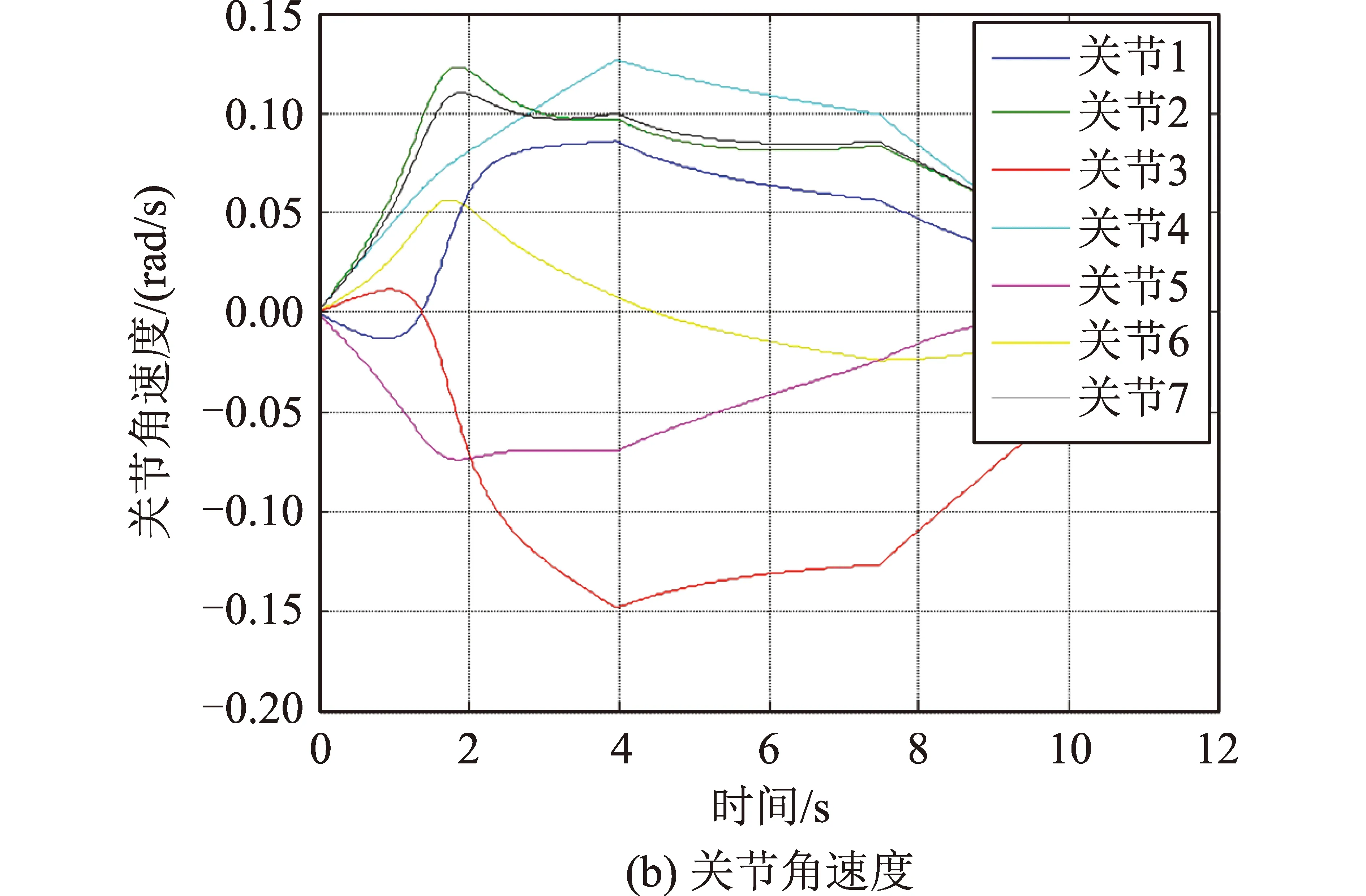
圖3 基于構型1的軌跡規劃Fig.3 Trajectory planning based on configuration 1

當機械臂初始構型為[3.80 0.01 -5.14 -1.28 1.05 1.56 -0.01]T時，反作用力矩峰值達到最小為18.16 Nm，將此構型記為構型2，基于構型2進行路徑規劃得到的關節運動狀態如圖4所示。

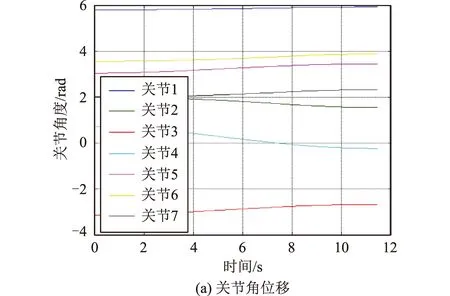
圖4 基于構型2的軌跡規劃Fig.4 Trajectory planning based on configuration 2

兩種初始構型下的基座反作用力矩對比如圖5所示，對比發現，按照兩種初始構型對機械臂進行路徑規劃時，兩者在笛卡爾空間的軌跡是完全一樣的，但是在運動過程中機械臂的構型卻大不相同，對基座產生的反作用峰值力矩相差近50%，且構型1對應的關節角速度遠大于構型2。仿真表明，按照初始構型2進行軌跡規劃的效果優于構型1。圖6和圖7分別為基于構型1和構型2規劃的直線軌跡。

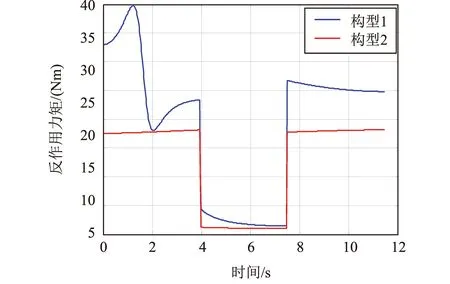
圖5 兩種初始構型下的基座反作用力矩對比Fig.5 Comparison of base reaction moments under two initial configurations

圖6 基于構型1規劃的軌跡Fig.6 Trajectory planning based on configuration 1

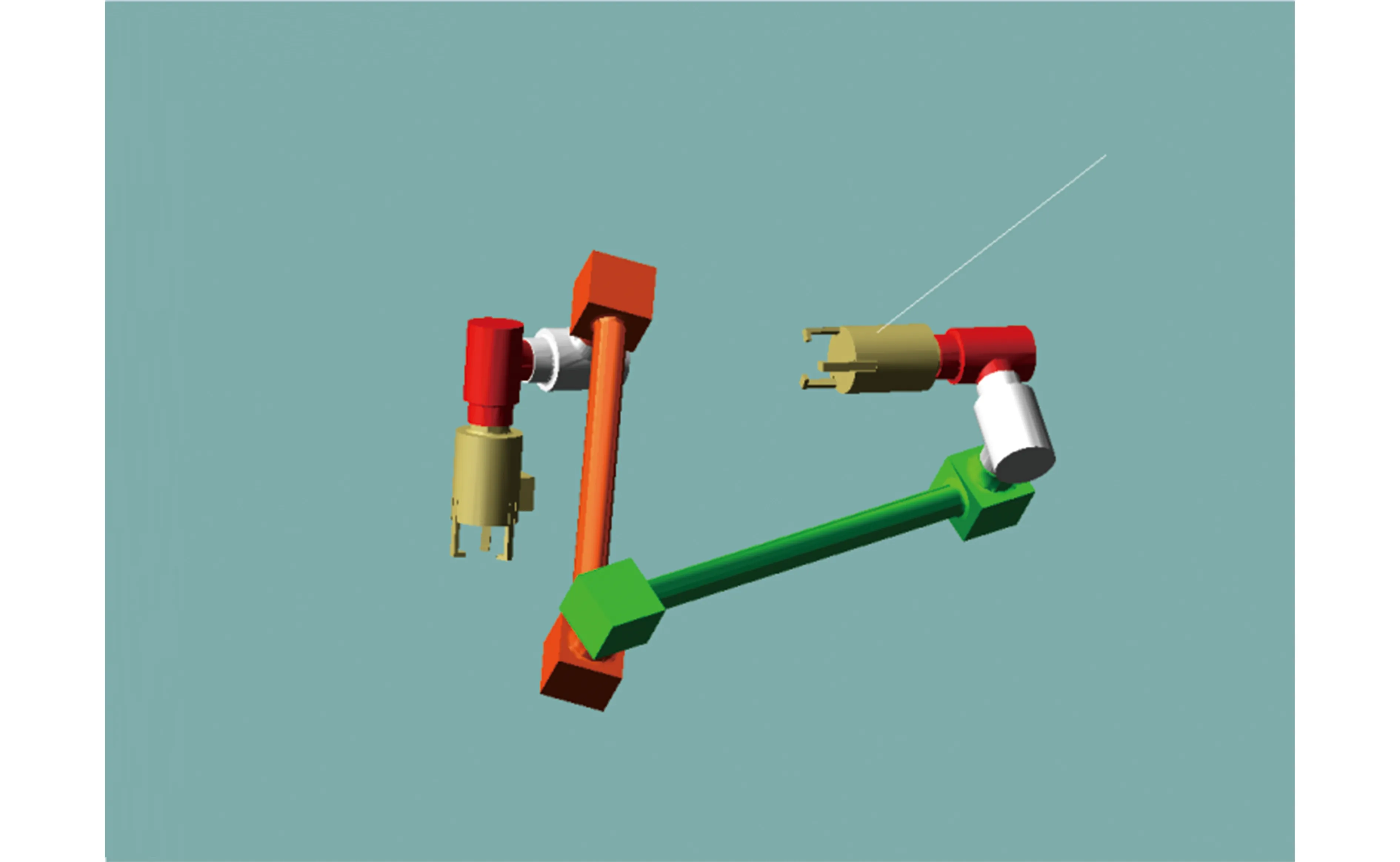
圖7 基于構型2規劃的軌跡Fig.7 Trajectory planning based on configuration 2

對于零負載和3 t負載的情況，同樣按照本文第2節所述的流程進行計算，仿真結果表明分別基于構型1和構型2進行規劃會使反作用力矩峰值達到最大和最小，兩種構型下基座受到的反作用力矩如圖8所示。對于固定基座和同樣的速度曲線，不同質量的負載只會引起負載慣性力的變化，將其解算至各關節然后疊加空載關節力矩，遞推可得到基座的反作用力矩，因此無論末端負載多大，基于構型2進行規劃產生的反作用力矩峰值均小于構型1。

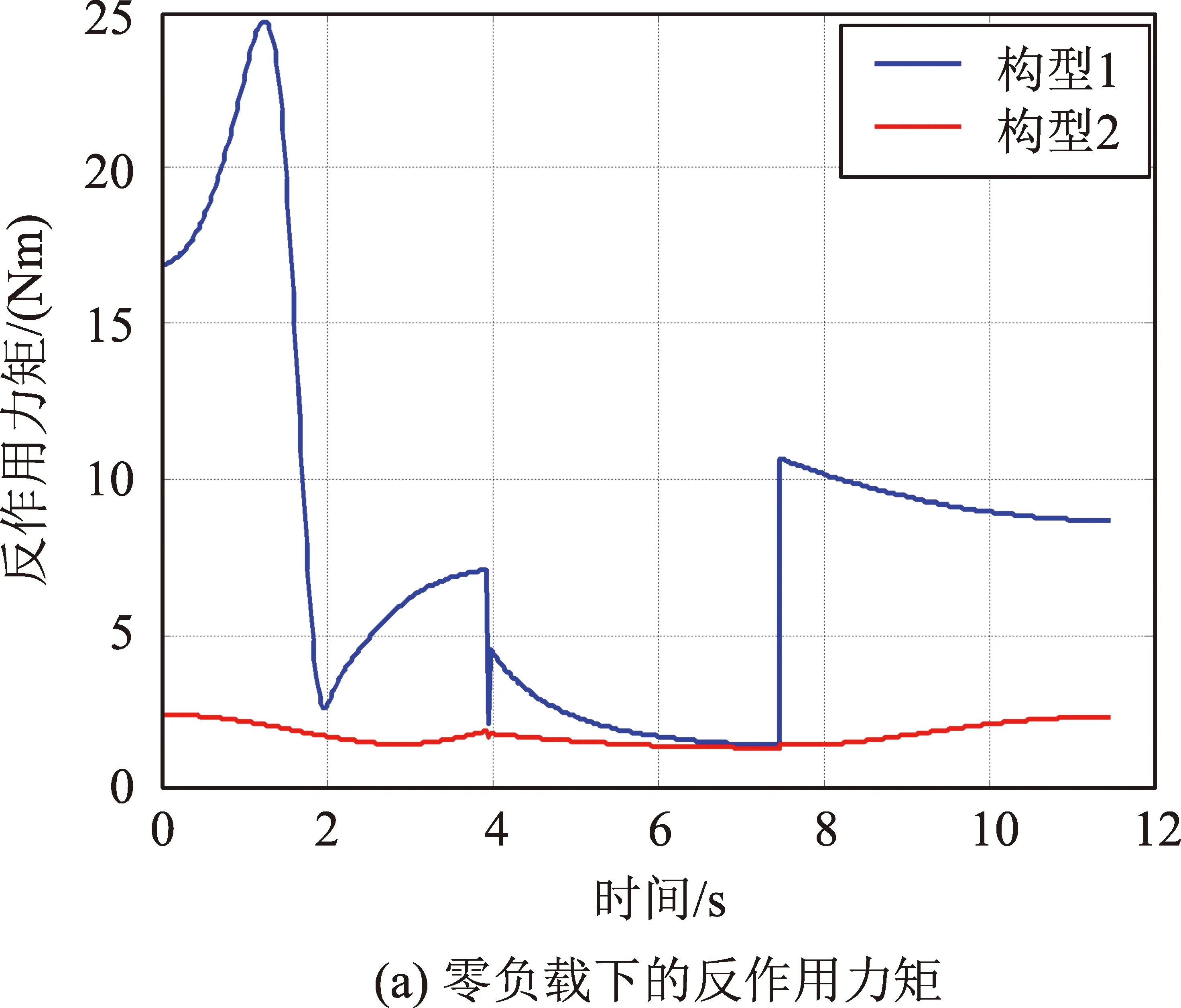
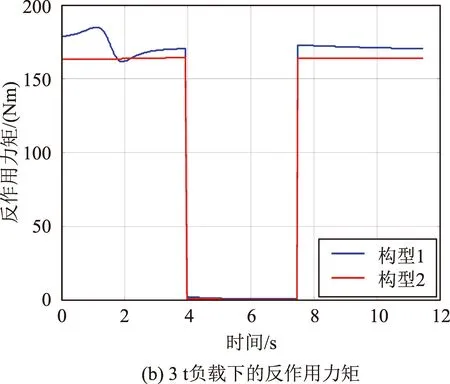
圖8 不同初始構型下的基座反作用力矩比較Fig.8 Comparison of base reaction moments under different initial configurations

4 結束語

基于不同的初始構型對七自由度空間機械臂進行了直線規劃，研究了機械臂初始構型對基座反作用力矩的影響。通過仿真得出的結論為：①對于笛卡爾空間的某一條規劃軌跡，通過調整機械臂的初始的構型,能大幅減小機械臂在運行過程中對基座產生的反作用力矩。當機械臂末端負載分別為0、300 kg和3 t時，通過調整初始構型能使航天器平臺受到的反作用力矩峰值減小88%、54%和11%。②在工程實際中，根據本文方法能夠在機械臂無數的初始構型中找到一種最優的構型，基于此構型進行笛卡爾空間的軌跡規劃時，使得機械臂在運動過程中航天器平臺受到的反作用力矩峰值最小，因此減小了干擾力矩超出反作用飛輪控制力矩從而造成航天器姿態失控的風險。