基于層次分析法的異形結構清水混凝土模板選型研究

沈 婕 馬凱悅 丁小彬

(1.廣州地鐵集團有限公司，廣州 510030；2.廣州市設計院，廣州 510620；3.華南理工大學 土木與交通學院，廣州 510641)

引言

清水混凝土模板施工技術在清水混凝土的施工環節中屬于核心工序，關系到建筑整體性能的效率和整個建筑的質量，而模板選型是確保清水混凝土施工質量及其飾面效果的關鍵因素。目前這類模板的選型方法一般是采取比較法、經驗判斷法、單因素對比法等，未從整體考慮所有關鍵影響因素，最終選型的模板體系往往導致成本超支、材料浪費、質量低下等現象。因此，如何系統全面地進行異形結構清水混凝土模板選型是亟需解決的問題。

1 清水混凝土模板

1.1 概念

清水混凝土是直接利用現澆混凝土一次澆注成型，不做任何外裝飾，直接由結構混凝土自身的自然顏色、紋理與質感作為飾面效果的混凝土。清水混凝土模板是能保證達到清水混凝土成型質量要求和外觀裝飾效果進行設計加工的模板技術。

1.2 種類及優缺點

清水混凝土模板按材料組成分為竹木膠合板模板、全鋼大模板、鋼木組合模板、鋁合金模板、新型塑料模板及玻璃鋼模板等六大類，其優缺點對比如表1所示。

表1 清水混凝土模板種類及優缺點對比Table 1 Advantages and disadvantages of kinds of fair-faced concrete formwork

1.3 適用范圍

清水混凝土主要分為普通清水混凝土、飾面清水混凝土、裝飾清水混凝土三類，建議選擇的模板類型如表2所示。

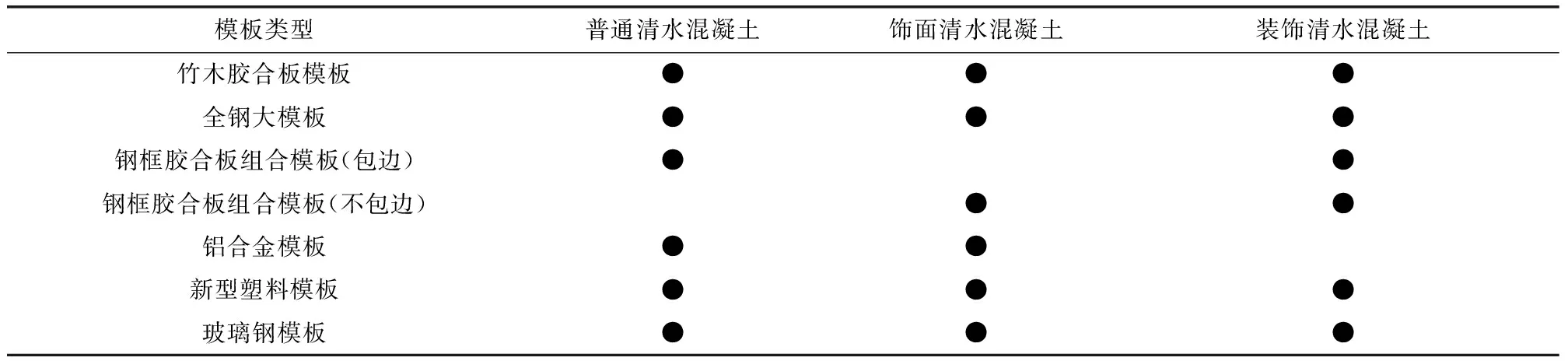
表2 清水混凝土模板適用范圍Table 2 Scope of application for fair-faced concrete formwork

2 異形結構清水混凝土模板研究綜述

對歷年國內外有關異形結構清水混凝土模板的應用領域和選型原則的文獻研究進行歸納總結，總結如表3-4所示。

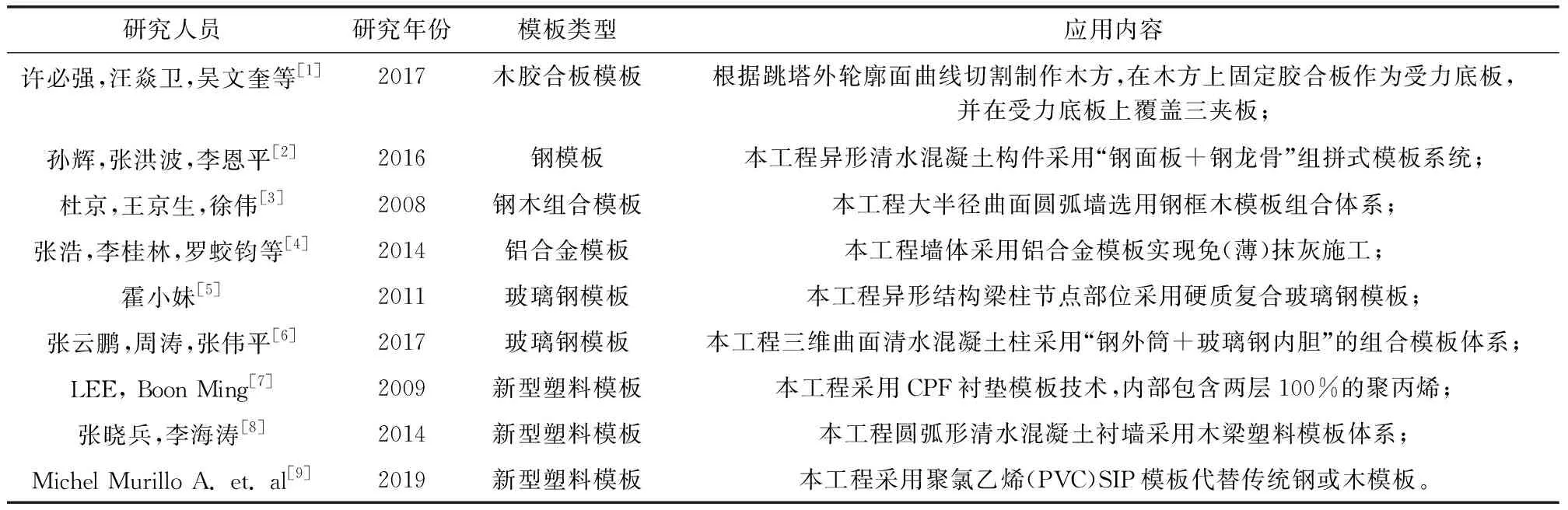
表3 異形結構清水混凝土模板類型應用研究綜述Table 3 Application overviews of kinds of fair-faced concrete formwork

表4 清水混凝土模板選型原則研究綜述Table 4 Research review on fair-faced concrete formwork selection

通過以上綜述可以得出，異形結構清水混凝土模板種類主要有木膠合板模板、鋼模板、鋼木組合模板、鋁合金模板、玻璃鋼模板和新型塑料模板； 該模板選型原則歸類為工程自身要求、成品質量、經濟、進度和安全性等五大因素。

3 基于層次分析法的異形結構清水混凝土模板選型

層次分析法(Analytic Hierarchy Process)，簡稱AHP，是美國運籌學家沙旦(T. L. Saaty)于20世紀70年代初提出的一種定性與定量分析相結合的層次權重決策分析方法[18]，其基本步驟是將有關決策的元素劃分為目標層、準則層和方案層，通過兩兩比較形成一個遞階有序的層次分析模型，計算出方案層對目標層的相對權重值進行方案優劣性排序，最后從候選方案中選出最優方案。異形結構清水混凝土模板選型層次分析法基本步驟如圖1所示。

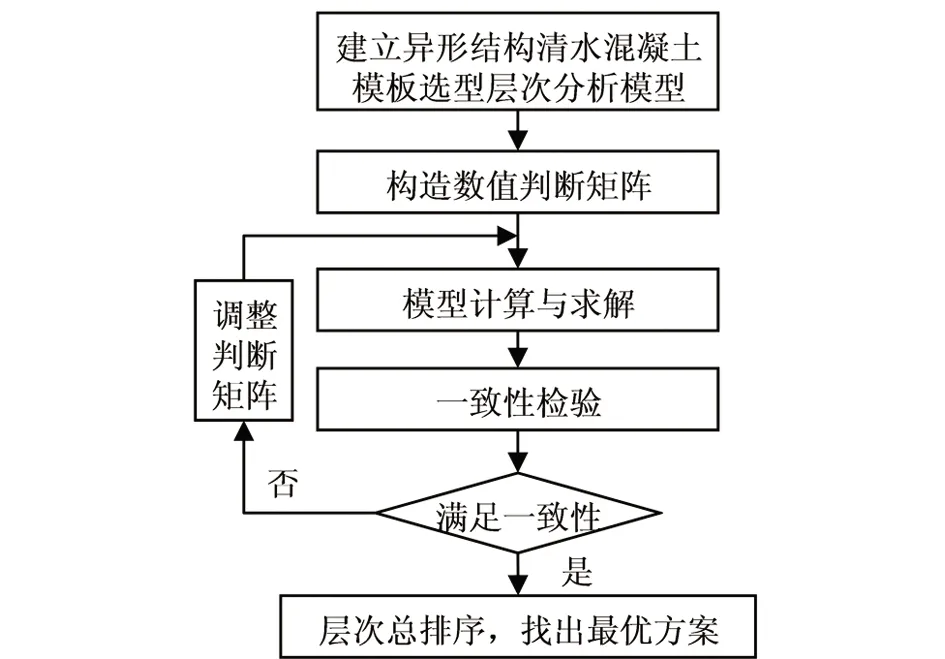
圖1 異形結構清水混凝土模板選型層次分析法基本步驟Fig. 1 Basic steps of AHP for type selection of special-shaped concrete formwork

3.1 建立層次分析模型

異形結構清水混凝土模板選型層次分析模型的建立過程就是將模板選型、關鍵影響因素和擇選方案相應設為決策目標、決策準則和決策對象，依次對應最高層(目標層Z)、中間層(準則層X)和最低層(方案層Y)，繪出層次結構圖(如圖2所示)。

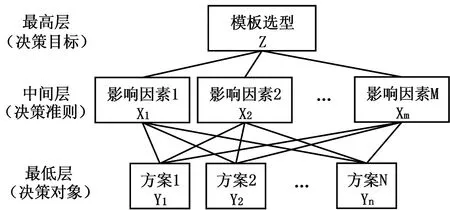
圖2 異形結構清水混凝土模板選型層次結構圖Fig. 2 Type selection hierarchy diagram of special-shaped concrete formwork

3.2 構造數值判斷矩陣

根據專家對各元素重要度的評判結果，運用成對比較法和1-9位標度法求出準則層每個因素相對于目標層的相對權重，構造出各元素之間重要度關系的數值判斷矩陣。其中，標度aij表示因素i與因素j的重要性比較結果，所表示的含義如表5所示。

表5 標度值及其含義Table 5 The meaning of scale values

3.3 模型計算與求解

在層次分析法中，對判斷矩陣的特征向量和最大特征值計算求解有三種方法：和法、根法和冪法。本文采用方根法對異形結構清水混凝土模板選型層次分析模型進行計算。

1)對指標進行兩兩比較，確定其相對重要性，構成判斷矩陣A：

其中，aij>0，aji=1/aij，aii=1

2)計算判斷矩陣每行各元素的幾何平均數：

(1)

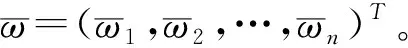
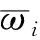
(2)

得到特征向量ω=(ω1，ω2，…，ωn)T，即各因素的相對權重值。

4)計算數值判斷矩陣的最大特征值λmax：

(3)

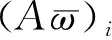
3.4 一致性檢驗

一致性檢驗是評價權重排序是否科學合理、計分合理與否的基本指標。如若檢驗通過，歸一化后的特征向量則為權重向量； 如若檢驗未通過，則需要對判斷矩陣做出適當修改直至取得令人信服的一致性為止。一致性檢驗需引入一致性指標CI和一致性檢驗系數CR。其計算公式如下：

(4)

(5)

其中，RI為隨機一致性指標。

當CR<0.1，時，認為判斷矩陣通過一致性檢驗。當CR≥0.1時，判斷矩陣的一致性是不被接受的，需作適當修正直至一致性檢驗通過。

表6 RI隨機一致性指標表Table 6 Table of RI random consistency indicators

3.5 層次總排序，找出最優方案

對通過一致性檢驗的權重結構進行分析，采取專家評判法對各個因素的重要程度進行確定后，進行方案層的組合權重計算，從而得出最優方案。組合權重計算公式如下：

(1)目標層Z相對準則層X的相對權重為：

ω(1)=(ω1(1)，ω2(1)，…，ωn(1))T

(6)

(2)準則層X對方案層Y中m個方案的相對權重為：

ωq(2)=(ω1q(2)，ω2q(2)，…，ωmq(2))T

q=1，2，…，n

(7)

(3)方案層Y對目標層Z而言，其相對權重是通過權重ω(1)與ωq(2)(q=1，2，…，n)組合而得到的，其計算表格如表7所示。

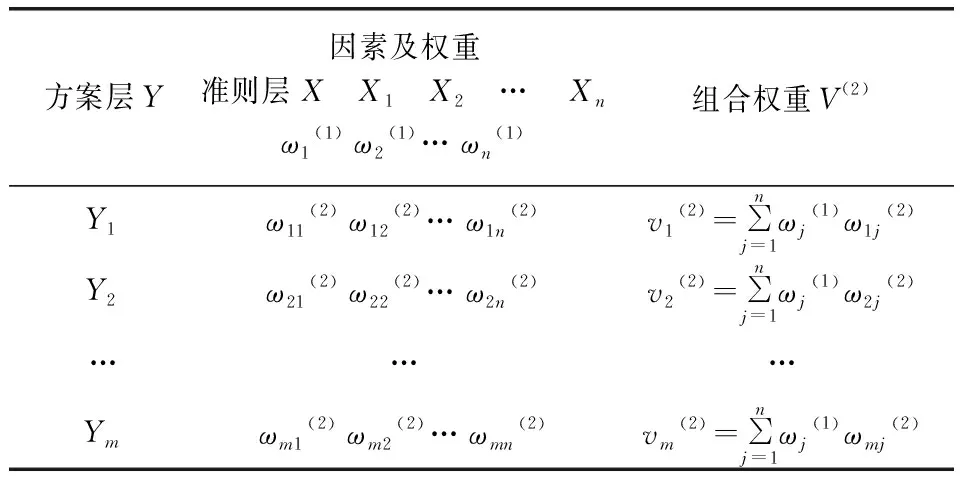
表7 組合權重Table 7 Combination weight

其中，V(2)=(v1(2)，v2(2)，…，vm(2))Τ為方案層Y中m個方案的相對權重。對各方案的權重值進行比較，權重值較大的則為最優方案。

4 案例研究

4.1 工程概況

浙江省黃龍體育中心游泳跳水館項目位于杭州市西子湖畔，為2022年杭州亞運會比賽場館，總建筑面積約4.9萬m2。本工程為重要，質量要求高、工期緊、用地緊張，跳水臺為該工程施工中的重難點，因此如何保證跳水臺快速高質量施工，是整個工程能否順利交工的關鍵。

4.2 跳水臺結構概況

本工程所用跳臺為1柱4臺型，高度分別為3m、5m、7.5m和10m。跳臺造型復雜，中心立柱較高且為變截面柱，跳臺與中柱過渡區間線面關系呈非幾何非線性復雜關系，由10個回轉曲面和6個非回轉曲面構成。跳水臺為C40清水混凝土結構，需一次澆筑成型，對模板自身強度、剛度和穩定性及面層處理要求很高，其清水混凝土結構成型質量及外觀效果要求高。因此，跳臺結構的模板選型對其成型質量和清水混凝土的裝飾效果十分重要。

4.3 構建跳水臺模板選型模型

本文直接將研究對象設為目標層，即確定以清水混凝土跳水臺模板選型，從而構建出清水混凝土跳水臺模板選型層次分析模型(如圖3)。

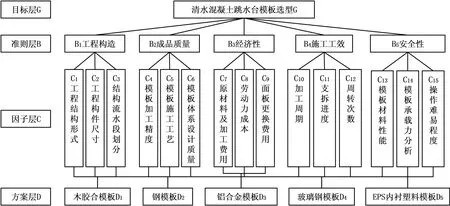
圖3 跳水臺模板選型層次分析模型Fig. 3 Analytic hierarchy model of diving platform formwork selection

4.4 構造判斷矩陣并進行一致性檢驗

根據跳水臺模板選型層次分析模型(圖3)建立調查問卷表，以網絡發放的形式邀請建筑行業施工專家、結構設計專家、各模板廠家技術專家等進行打分，對他們的意見和建議進行數據收集。之后，采用SPSS軟件進行數據可靠性分析，測得可靠性指標α>0.9136，表示信度檢驗滿足要求。

1)準則層關于目標層的相對權重

采用方根法計算準則層B關于目標層G的相對權重，步驟如下：

①通過專家打分，對準則層兩兩比較得到的判斷矩陣為：

②利用式(1)計算判斷矩陣每行的幾何平均數為：

③利用式(2)進行歸一化計算特征向量為：

ω(1)=(0.0358，0.3840，0.1753，0.1225，0.2822)Τ，即準則層關于目標層G的相對權重。

④利用式(3)計算判斷矩陣的最大特征值λmax為：

⑤利用式(4)對所得結果進行一致性檢驗：

根據表6查得，當n=5時，隨機一致性指標RI=1.12，可以得出：

因此可得出，判斷矩陣滿足一致性，所求的權重是具有科學性與合理性的。

同理，可計算出各因子層相對于目標層的總權重值，如表8所示。

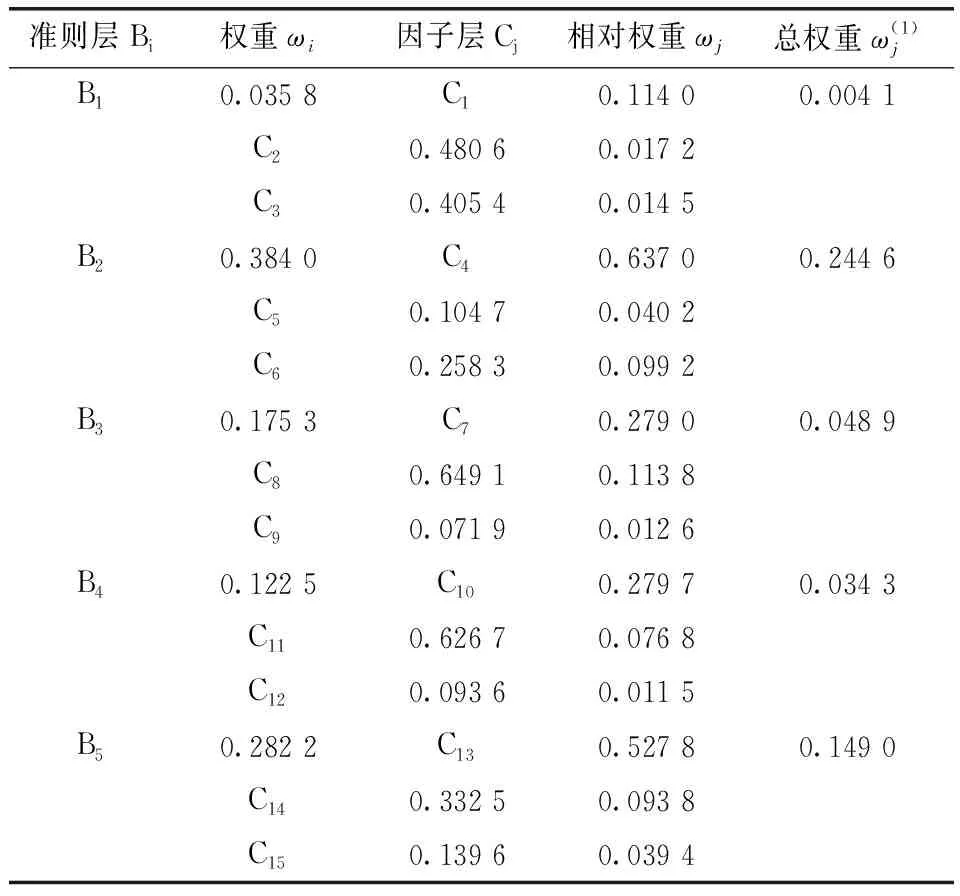
表8 準則層、因子層關于目標層的相對權重Table 8 The relative weight of the criterion layer and the criterion layer with respect to the target layer

2)方案層關于因子層的相對權重

通過專家打分，分別構造出因子層C1～C15下的判斷矩陣A1～A15，計算過程僅以模板材料性能(C13)進行舉例，計算步驟如下：

①通過各方案兩兩比較得到的判斷矩陣為：

②利用式(1)計算判斷矩陣每行的幾何平均數為：

③利用式(2)進行歸一化計算特征向量為：

ω(2)=(0.0359，0.1408，0.1021，0.3267，0.3946)Τ，即方案層關于因子層C13的相對權重。

④利用式(3)計算判斷矩陣的最大特征值為：

⑤利用式(4)對所得結果進行一致性檢驗：

根據表6查得，當n=5時，隨機一致性指標RI=1.12，可以得出：

因此可得出，判斷矩陣滿足一致性，所求的權重是具有科學性與合理性的。

同理，可計算出各因子層下五個方案的相對權重，如表9所示。

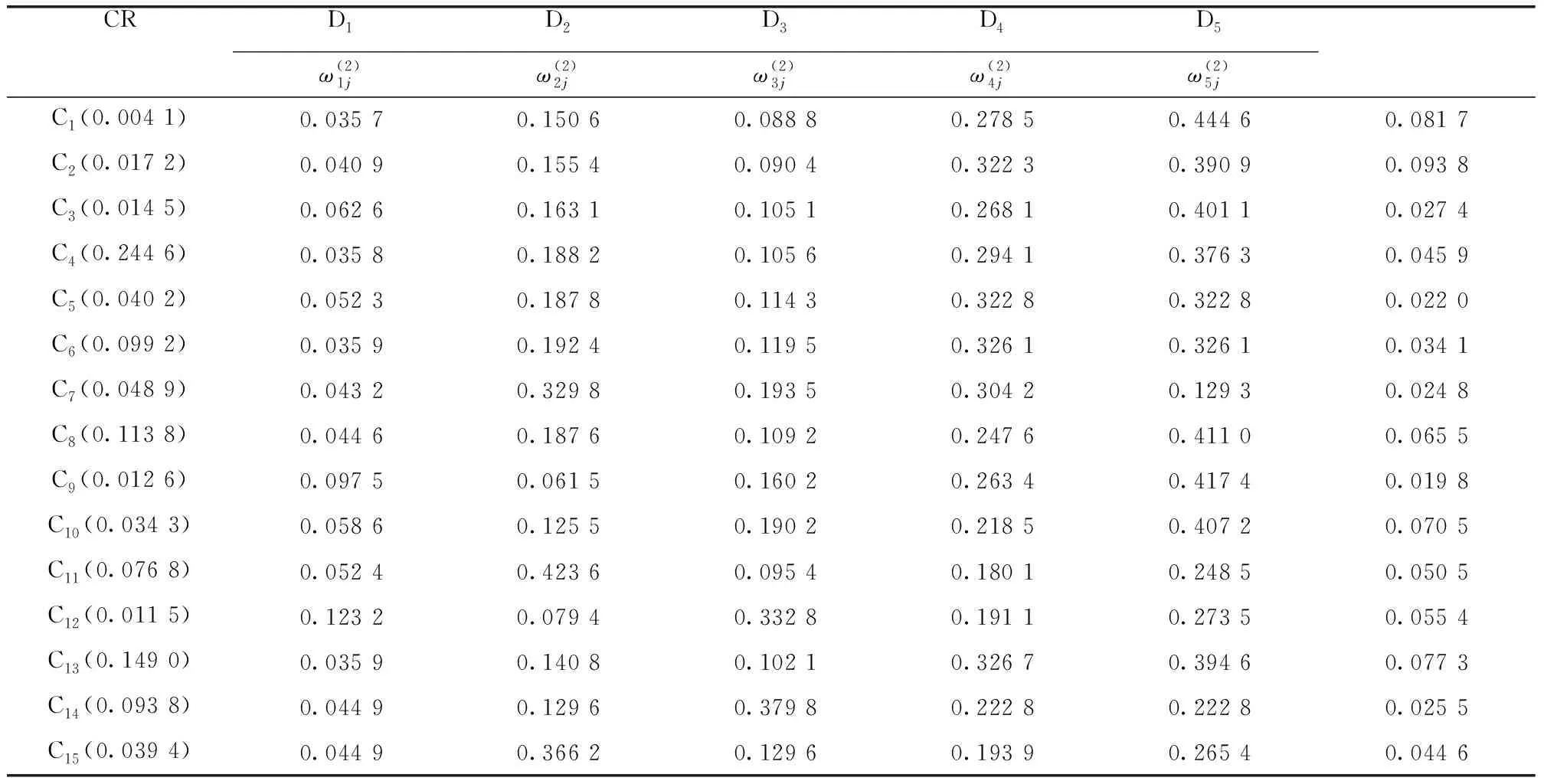
表9 方案層關于因子層的相對權重Table 9 The relative weight of the scheme layer with respect to the criterion layer

4.5 確定合成權重向量

層次分析模型的構建目的就是要計算出方案層關于目標層的相對權重，最終比選出最優方案。為此，按照表7將因子層關于目標層的相對權重與方案層關于各因子層的相對權重進行合成，即可得出方案層關于目標層的相對權重，計算如下：

同理，可計算出：v2(2)=0.2019，v3(2)=0.1321，v4(2)=0.2750，v5(2)=0.3577。

因此，可得出結論：異形空間曲面清水混凝土跳水臺模板選型為EPS內襯塑料模板。根據文獻綜述和市場調研，基于傳統施工經驗較多選用定制鋼模板對跳水臺進行施工，雖然其成型效果俱佳，但其造價高、成型需要模具、吊裝要求高、拆裝不便、材料節約等方面都不及EPS內襯塑料模板。

5 結論

本文利用層次分析法構建出清水混凝土跳水臺模板選型的層次分析模型，通過求解判斷矩陣的特征向量和最大特征值，進而確定出木膠合模板、鋼模板、鋁合金模板、玻璃鋼模板和EPS內襯塑料模板五種模板方案的相對權重值，最終選定EPS內襯塑料模板。該模板在工程構造、成品質量、經濟性、施工工效及安全性等方面的綜合性能優于其它四種模板方案，符合跳水臺工程的設定目標及要求。同時，基于層次分析法進行清水混凝土跳水臺模板方案優選的解決思路，適用于同類異形跳水臺結構模板選型決策問題，同時也為建設工程領域異形清水混凝土結構的模板選型提供了一定的理論和方法指導。