基于“等功”原理的滾動(dòng)體導(dǎo)向面設(shè)計(jì)方法及振動(dòng)性能分析
榮伯松, 宋現(xiàn)春, 王繼坤, 姜洪奎
(1.濟(jì)寧技師學(xué)院 機(jī)電工程系,山東 濟(jì)寧 272100; 2.山東建筑大學(xué) 機(jī)電工程學(xué)院,濟(jì)南 250101;3.國(guó)家機(jī)床質(zhì)量監(jiān)督檢驗(yàn)中心,北京 100102)
隨著機(jī)床向高速、重載方向發(fā)展,對(duì)滾柱直線導(dǎo)軌副的運(yùn)動(dòng)速度、承載性能及動(dòng)態(tài)性能的穩(wěn)定性提出了更高的要求,推動(dòng)滾動(dòng)直線導(dǎo)軌副的產(chǎn)品結(jié)構(gòu)、性能及產(chǎn)品制造工藝不斷提升。滾柱直線導(dǎo)軌副結(jié)構(gòu)圖,如圖1所示。
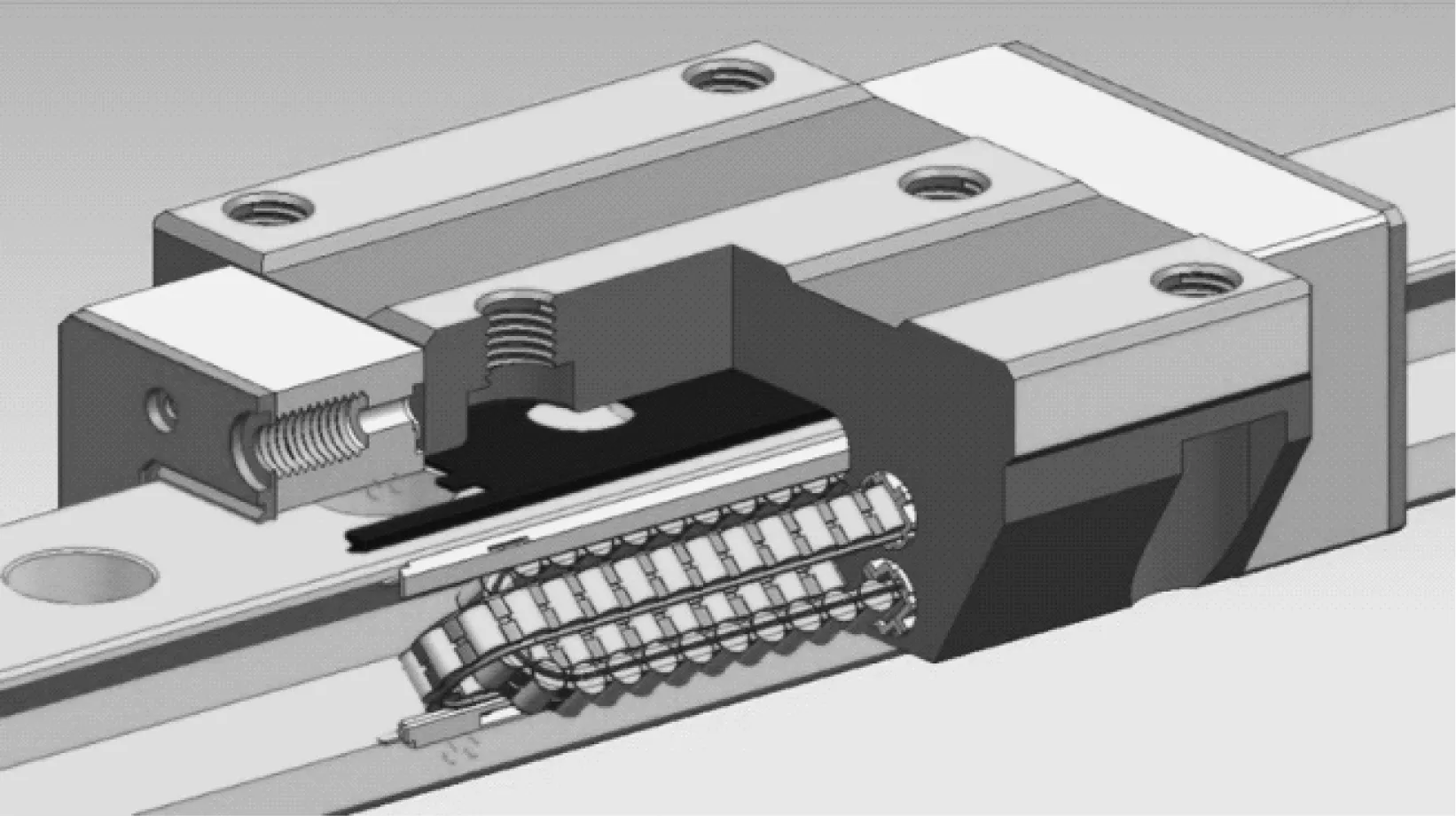
圖1 滾柱直線導(dǎo)軌副結(jié)構(gòu)圖
根據(jù)滾柱直線導(dǎo)軌副的工作原理可知,當(dāng)滾柱直線導(dǎo)軌副高速運(yùn)動(dòng)時(shí),滾動(dòng)體在承載區(qū)及返向區(qū)內(nèi)高速運(yùn)轉(zhuǎn),由于滾動(dòng)體在這兩個(gè)區(qū)域內(nèi)受力狀態(tài)不同,特別是在滑塊承受大負(fù)載時(shí),滾動(dòng)體進(jìn)入承載區(qū)前后的形變量增大,形變過程變短且劇烈程度變強(qiáng),導(dǎo)致滑塊運(yùn)動(dòng)振動(dòng)增大、噪聲增高,從而導(dǎo)致機(jī)床整體性穩(wěn)定性變差。隨著機(jī)床速度、承載及精度要求越來越高,如何減小滾柱直線導(dǎo)軌副運(yùn)動(dòng)振動(dòng)情況對(duì)提升機(jī)床的穩(wěn)定性十分關(guān)鍵[1-3]。
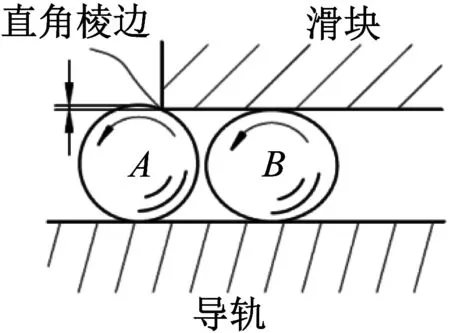
根據(jù)滾柱直線導(dǎo)軌副結(jié)構(gòu)可知,一般情況下滑塊的軌道端部,如圖2(a)所示。端部與滑塊的端面形成一個(gè)直角棱邊,滾柱進(jìn)入承載區(qū)時(shí)首先接觸到這個(gè)棱邊,由于接觸面小,滾柱與棱邊之間接觸應(yīng)力非常高,特別是在滑塊高速、重載條件下,滾柱與棱邊在極短的時(shí)間內(nèi)產(chǎn)生較大的接觸應(yīng)力,甚至超過材料的許用應(yīng)力,損壞滾柱表面,導(dǎo)致滑塊壽命降低,由于滾動(dòng)體的變形在較短的時(shí)間內(nèi)完成,極易造成滑塊運(yùn)動(dòng)振動(dòng)加劇,導(dǎo)致機(jī)床工作臺(tái)的穩(wěn)定性變差,影響工件的加工質(zhì)量[4-5]。
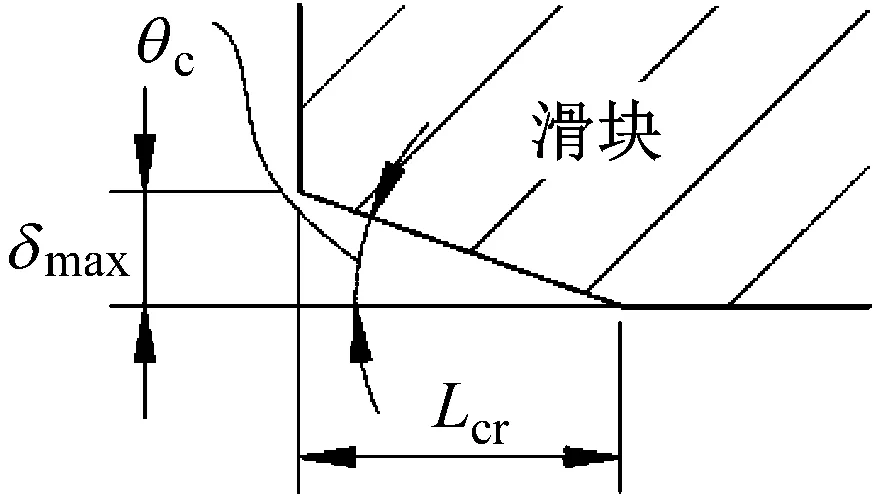
為了降低滑塊的運(yùn)動(dòng)振動(dòng)情況從滾動(dòng)體進(jìn)出承載區(qū)的過程入手,在滑塊軌道的端部設(shè)置導(dǎo)向面,如圖2(b)所示。提高滾動(dòng)體進(jìn)、出承載區(qū)的流暢性,降低滑塊的運(yùn)動(dòng)振動(dòng)。基于這種考慮經(jīng)過眾多學(xué)者的研究,首先將導(dǎo)向面設(shè)計(jì)成如圖3所示的結(jié)構(gòu)。其中圖3(a)所示為直線型導(dǎo)向結(jié)構(gòu),圖3(b)所示為圓弧型導(dǎo)向結(jié)構(gòu),這兩種導(dǎo)向面結(jié)構(gòu)簡(jiǎn)單,制作方便,但是對(duì)滾動(dòng)體進(jìn)入承載區(qū)過程的改善效果不理想,特別當(dāng)滾柱直線導(dǎo)軌副處于高速運(yùn)動(dòng)狀態(tài)時(shí)對(duì)產(chǎn)品運(yùn)動(dòng)流暢性及振動(dòng)的改善效果不理想,為此,Matsumoto等[6]建立了基于接觸應(yīng)力的導(dǎo)向過渡曲面計(jì)算模型,推導(dǎo)出導(dǎo)向面曲率的計(jì)算公式,以降低接觸面上的接觸應(yīng)力為目標(biāo),對(duì)導(dǎo)向過渡面的結(jié)構(gòu)形式進(jìn)行研究,并同時(shí)設(shè)計(jì)了多種導(dǎo)向面結(jié)構(gòu)形式,通過滑塊的振動(dòng)試驗(yàn)驗(yàn)證導(dǎo)向面結(jié)構(gòu)的效果。姜大志等[7-8]在對(duì)導(dǎo)軌副剛度研究時(shí)提出了一種基于“等剛度”和“等速度”的軌道導(dǎo)向面的設(shè)計(jì)方法,并通過試驗(yàn)對(duì)具有“等剛度”導(dǎo)向面滑塊的振動(dòng)情況進(jìn)行測(cè)試,與不具有導(dǎo)向面的產(chǎn)品進(jìn)行對(duì)比驗(yàn)證了導(dǎo)向面的實(shí)際效果。
(a)
(a) 直線型
本文將通過分析滾柱進(jìn)、出承載區(qū)時(shí)變形能的變化,推導(dǎo)建立一種基于“等功”原理軌道導(dǎo)向面的計(jì)算模型,降低滑塊的振動(dòng)及噪聲,并與其他形式的導(dǎo)向面結(jié)構(gòu)進(jìn)行對(duì)比,驗(yàn)證基于“等功”型導(dǎo)向面的實(shí)際應(yīng)用效果及優(yōu)越性[9-11]。
1 基于“等功”原理滑塊軌道導(dǎo)向面結(jié)構(gòu)設(shè)計(jì)方法
1.1 基于“等功”原理滾子進(jìn)出承載區(qū)的受力分析
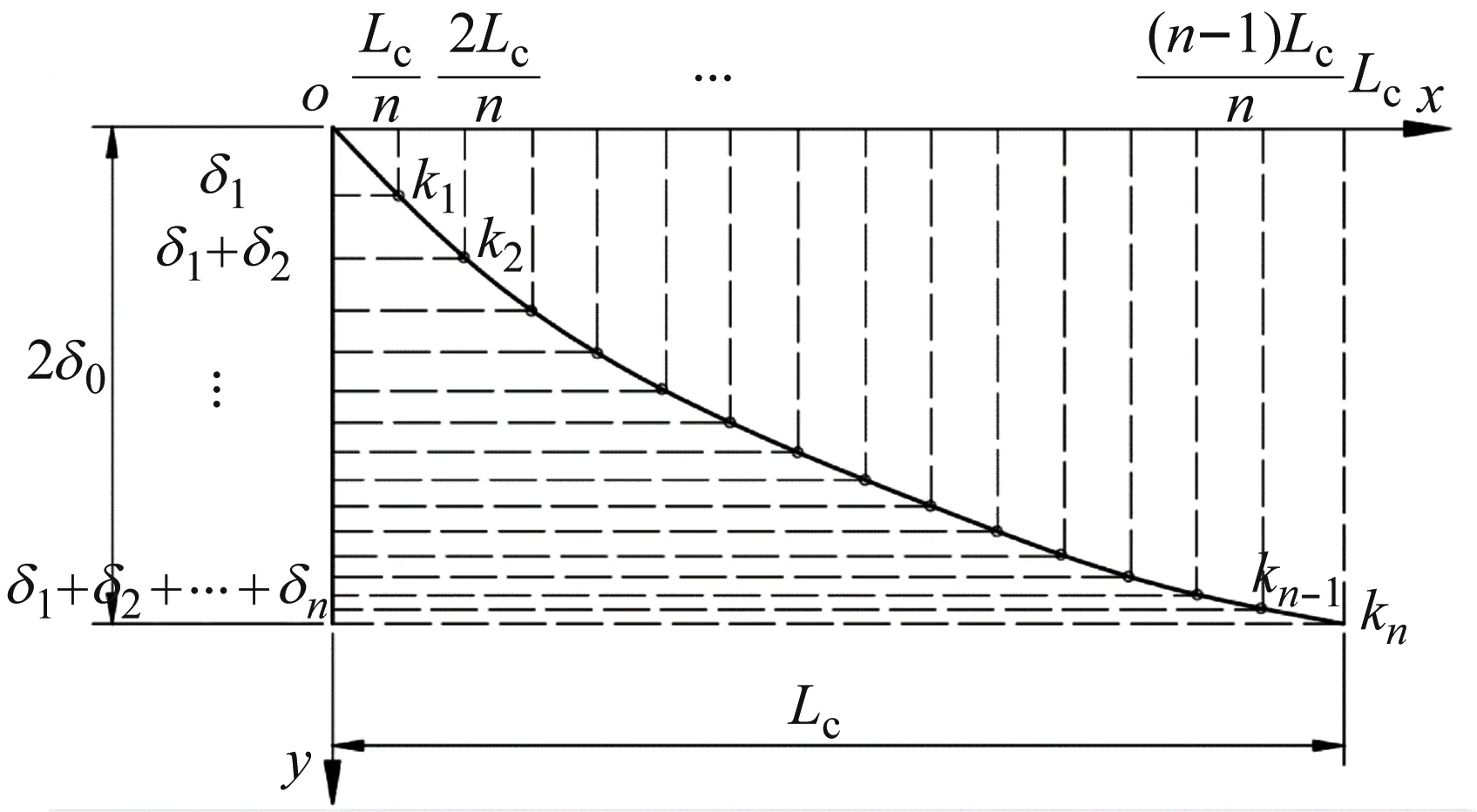
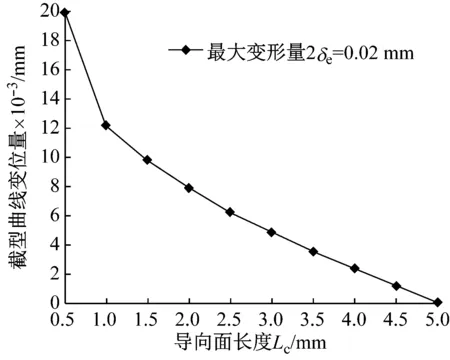
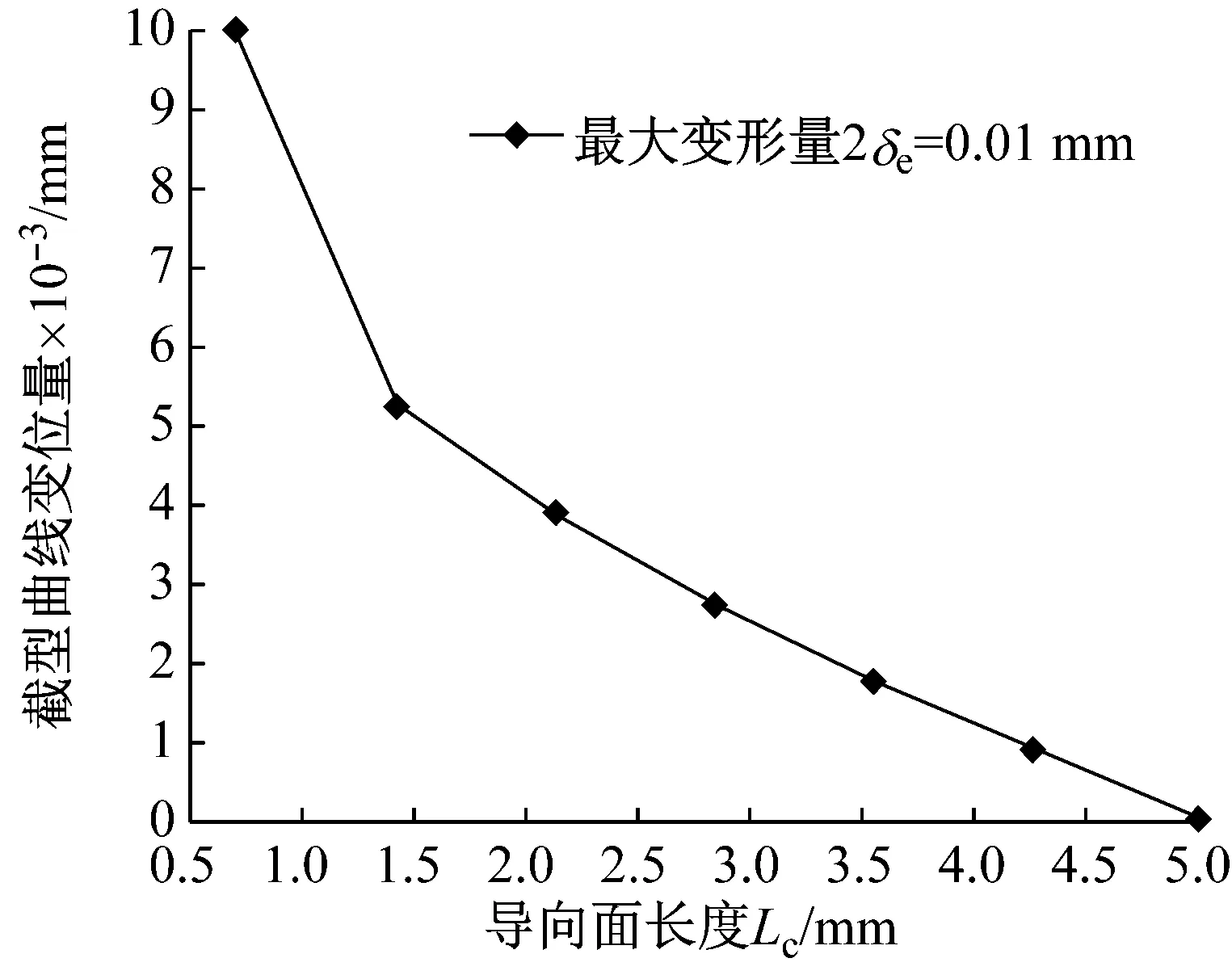
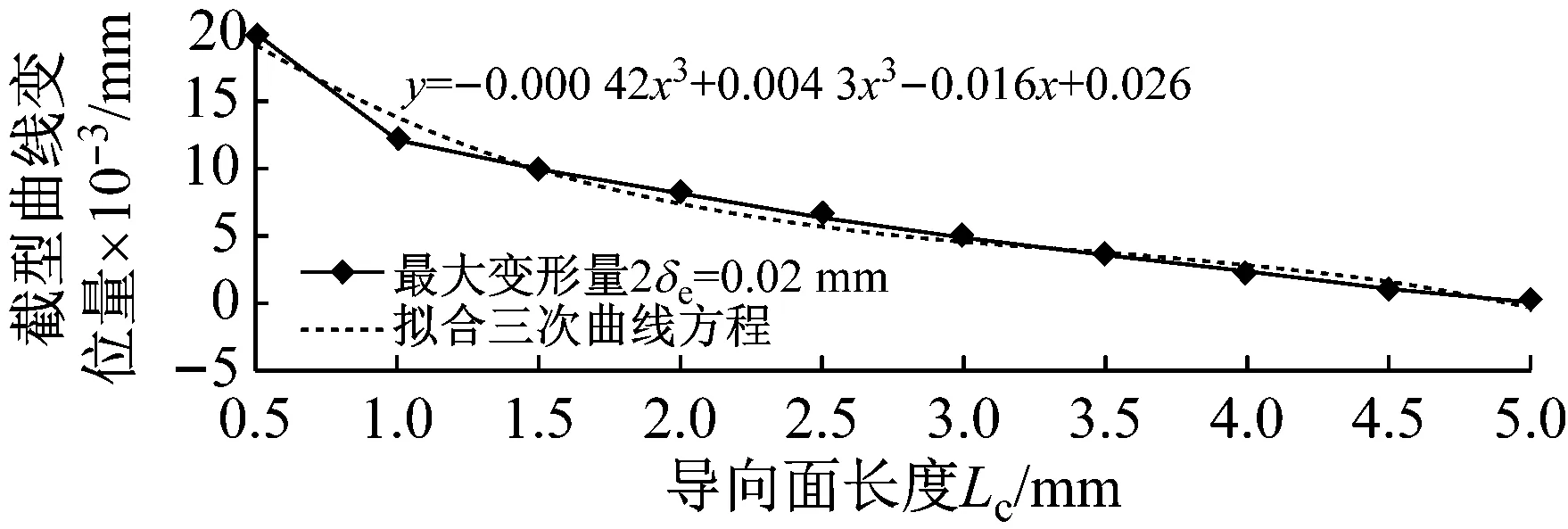
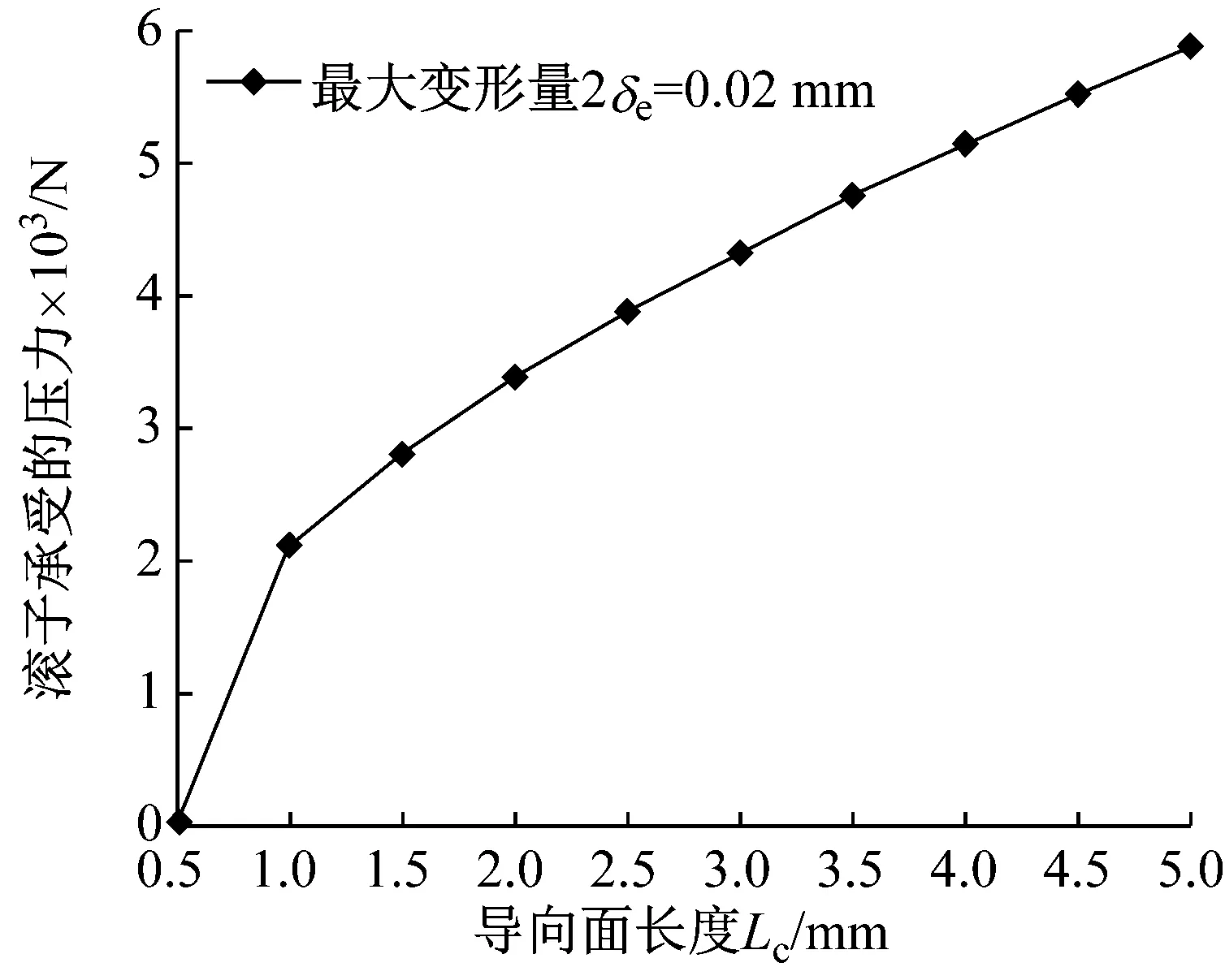
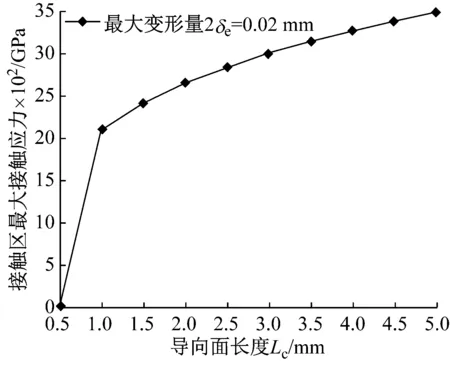
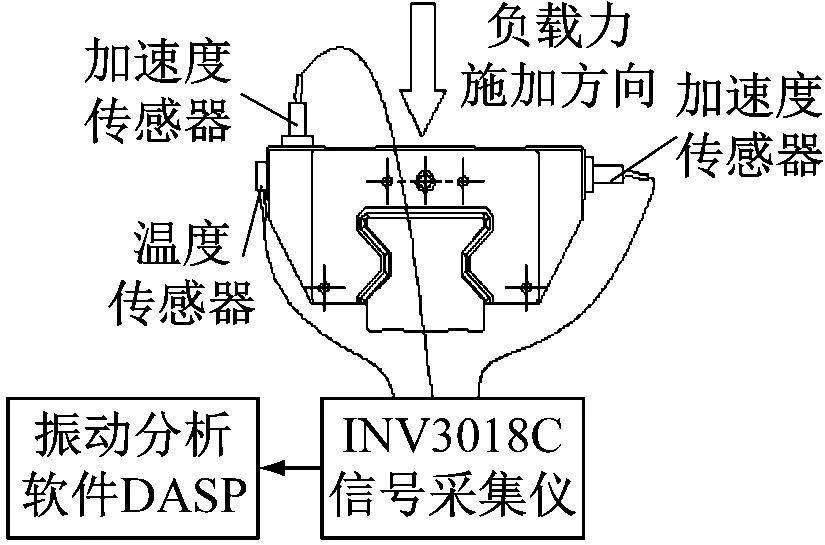
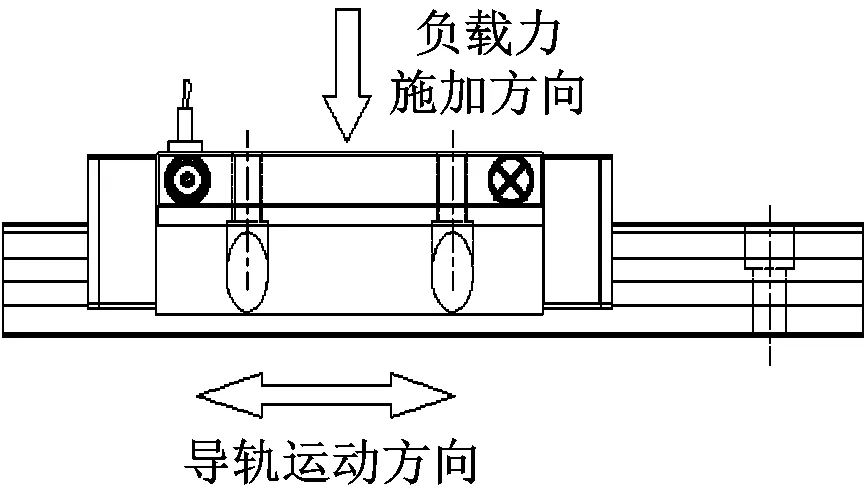
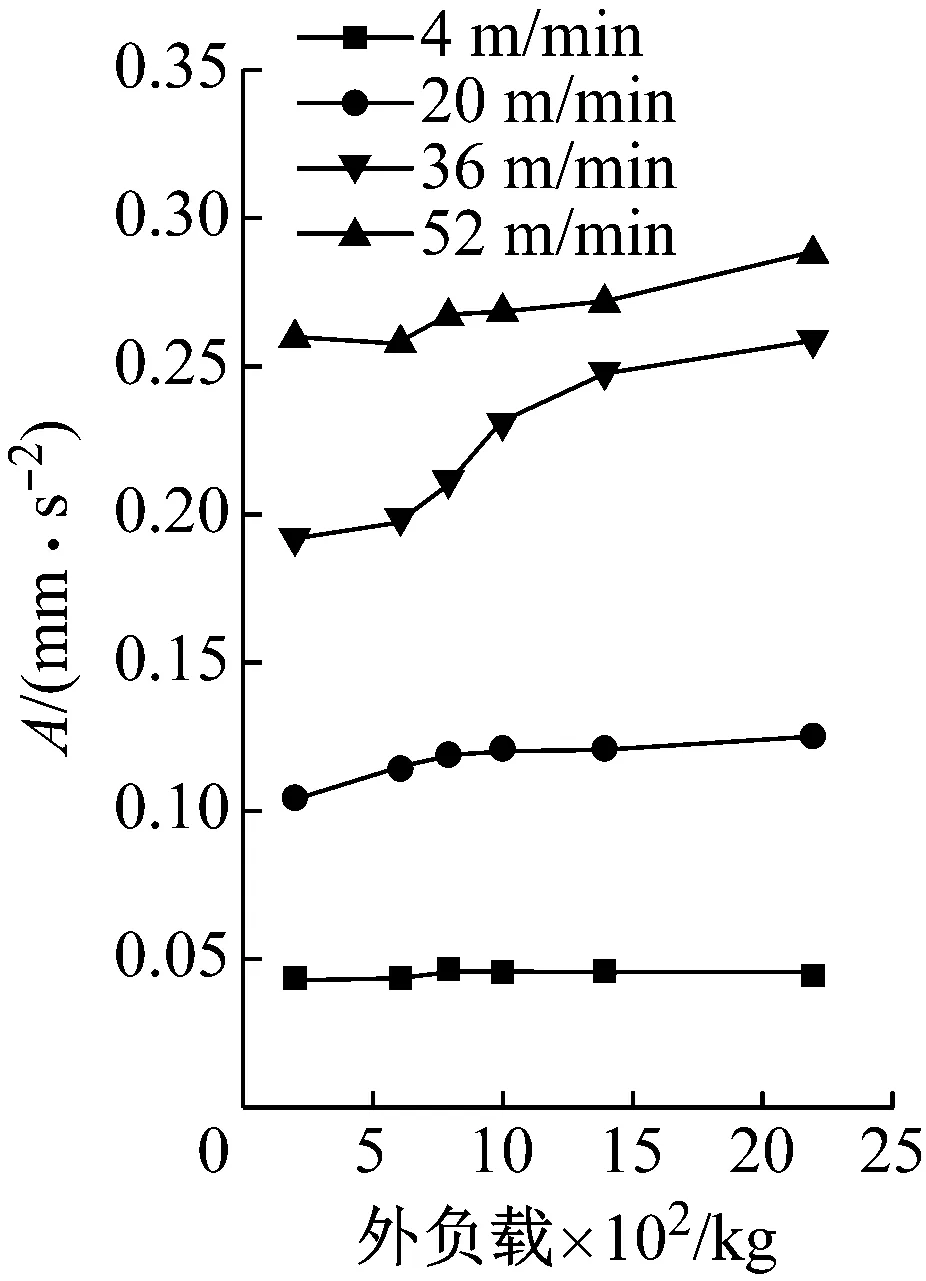
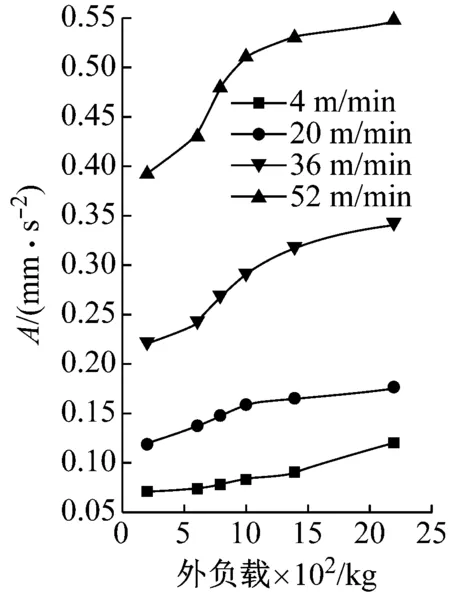
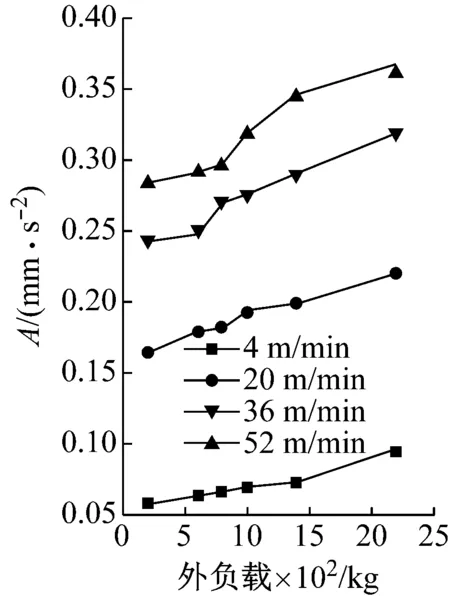
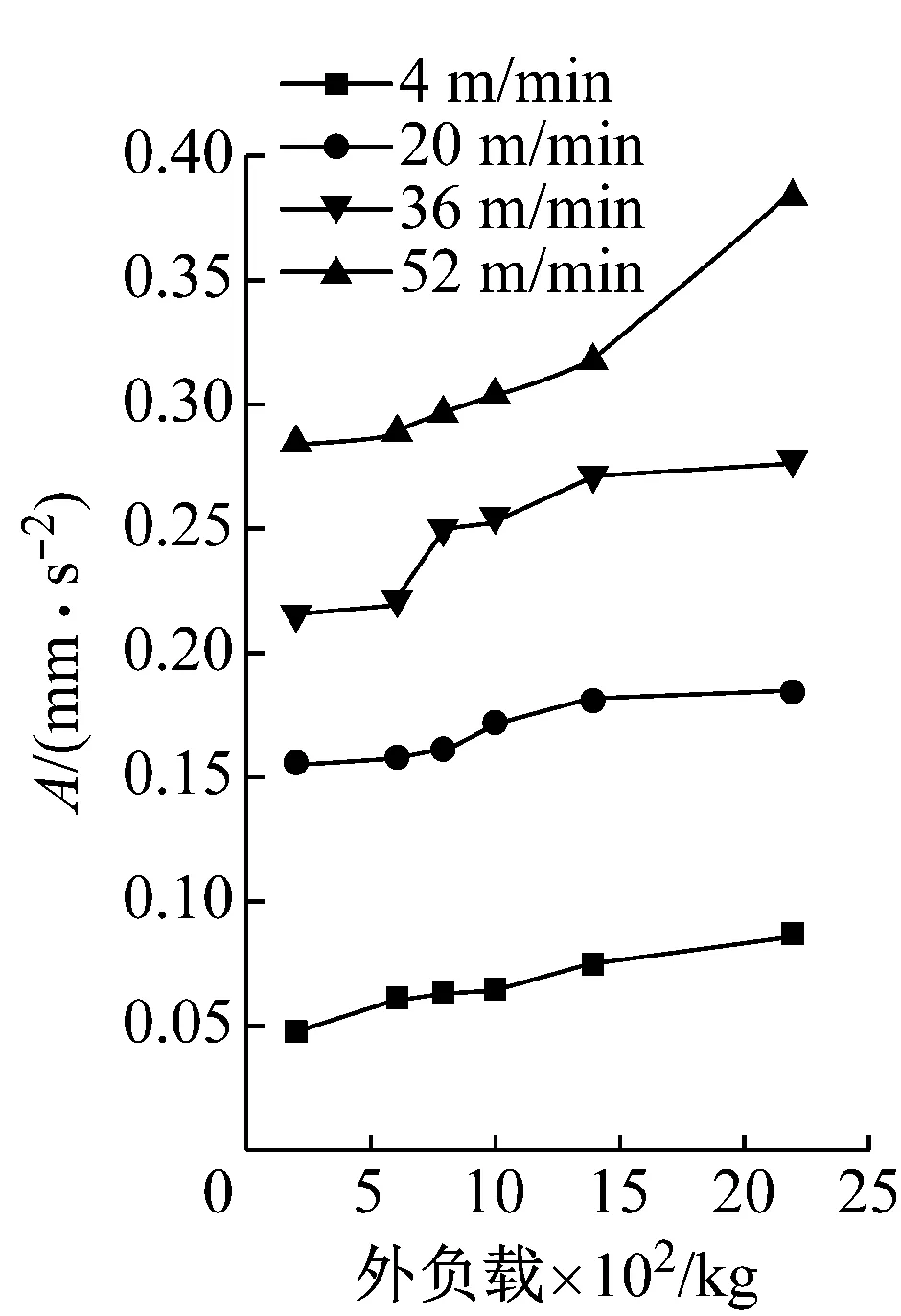
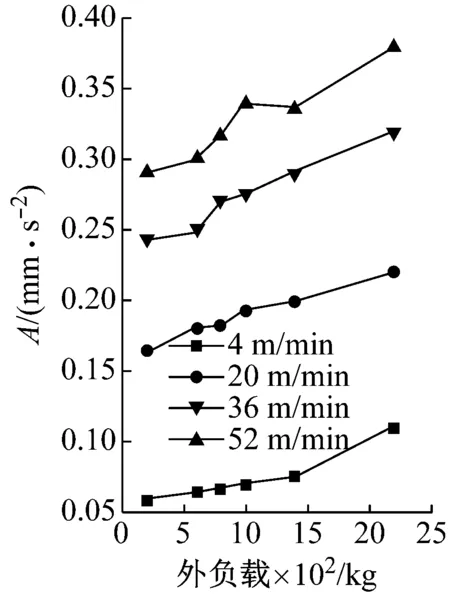
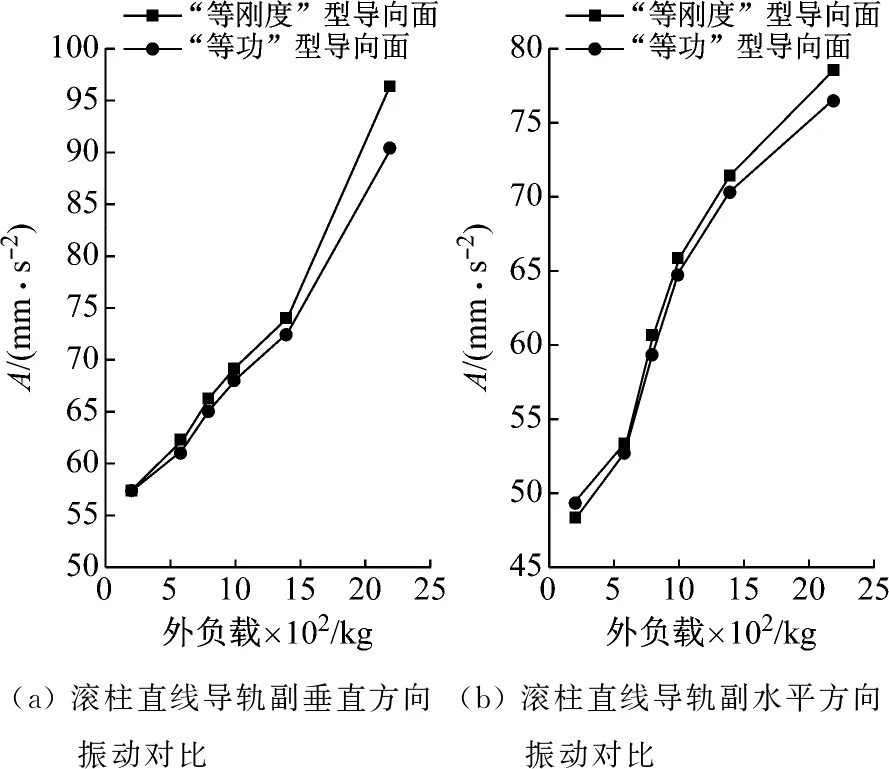
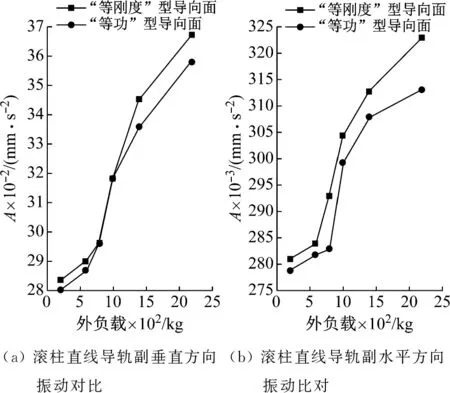
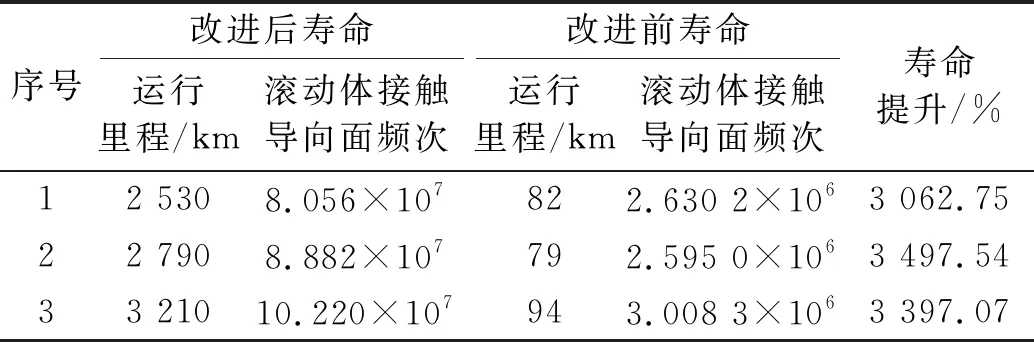
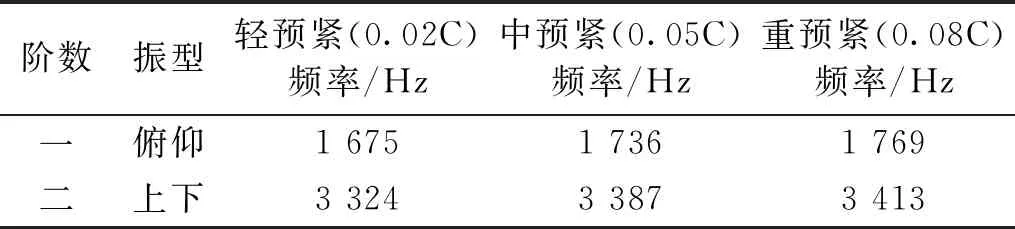
滑塊軌道與導(dǎo)軌軌道的間距為DG,滾柱直徑為Dw,一般情況下,為了提高滑塊的剛度,滑塊出廠時(shí)都會(huì)設(shè)置預(yù)緊力,即DG 圖4 滾柱進(jìn)入承載區(qū)受力示意圖 為了方便對(duì)滾柱進(jìn)入承載區(qū)過程的變形能進(jìn)行研究,將圖4所示滑塊勻速運(yùn)動(dòng)條件下滾柱與長(zhǎng)度為L(zhǎng)c的過渡區(qū)離散成接觸受力點(diǎn),各點(diǎn)之間的分布及坐標(biāo)關(guān)系,如圖5所示。滾柱勻速進(jìn)入承載區(qū)時(shí)與導(dǎo)向過渡面接觸點(diǎn)分別為k1,k2,k3,…,kn,坐標(biāo)分別為(δ1,Lc/n),[(δ1+δ2),2Lc/n],…,[(δ1+δ2+…+δn),Lc]。 圖5 等速運(yùn)動(dòng)條件下滾子與過渡區(qū)接觸受力點(diǎn) 設(shè)O點(diǎn)為導(dǎo)向面的起點(diǎn),滾柱從起點(diǎn)處與導(dǎo)向面相接觸,從O點(diǎn)移動(dòng)到k1點(diǎn)滾柱的變形能計(jì)算公式為 (1) 根據(jù)赫茲接觸理論可得接觸力與彈性形變的關(guān)系式 (2) 將式(2)代入式(1)可得 (3) 根據(jù)式(3)原理推得滾柱由k1運(yùn)動(dòng)至k2點(diǎn)時(shí)滾動(dòng)體變形能為 (4) 同理當(dāng)滾柱由kn-1運(yùn)動(dòng)至kn點(diǎn)時(shí)滾動(dòng)體變形能為 (5) 當(dāng)滾柱進(jìn)入導(dǎo)向區(qū)后,由于滑塊處于勻速運(yùn)動(dòng)狀態(tài),隨著滾動(dòng)體變形量越來越大,導(dǎo)致單位時(shí)間內(nèi)所需要的能量越大,從而影響滑塊驅(qū)動(dòng)力,為了消除這一影響,根據(jù)“等功”原理,即滾柱在圖5所示的每點(diǎn)之間運(yùn)動(dòng)時(shí)消耗的能量相同,可確保滑塊勻速運(yùn)動(dòng)時(shí)外驅(qū)動(dòng)力恒定不變,當(dāng)然這里的恒定不是絕對(duì)的,滾柱由自由狀態(tài)滾動(dòng)至k1點(diǎn)位時(shí)外部驅(qū)動(dòng)力會(huì)有一個(gè)增大的情況出現(xiàn),但是這個(gè)增大可根據(jù)實(shí)際使用情況進(jìn)行設(shè)定。 根據(jù)“等功”原理,結(jié)合式(1)~式(5)可得 (6) 式(6)在設(shè)定δ1后可求出其他各參數(shù)的數(shù)值,然后通過擬合計(jì)算出導(dǎo)向面截型曲線。 根據(jù)滾柱直線導(dǎo)軌副實(shí)際使用負(fù)載不超過額定載荷的30%可得滾柱單邊最大變形量δe=0.01 mm,過渡區(qū)最大變位量2δ0=2δe,取δ1=0.005 mm。當(dāng)滾柱單邊最大變形量為0.02 mm時(shí)基于“等功”原理獲得的導(dǎo)向曲面的截型曲線,如圖6所示。圖6中:橫坐標(biāo)為導(dǎo)向面的長(zhǎng)度;縱坐標(biāo)為導(dǎo)向面去除量的數(shù)值;由于滑塊勻速運(yùn)動(dòng),滾柱進(jìn)入承載區(qū)的速度也是勻速,因此橫坐標(biāo)是均勻取值。從圖6可知:隨著運(yùn)動(dòng)的進(jìn)行兩點(diǎn)之間垂直間距越來越小,單位時(shí)間內(nèi)垂直方向上的變形量越來越小。 圖6 當(dāng)滾柱單邊最大變形量為0.02 mm時(shí)導(dǎo)向過渡曲面截型曲線 當(dāng)滾柱單邊最大變形量δe=0.005 mm時(shí),滑塊軌道導(dǎo)向面截型曲線,如圖7所示。 圖7 當(dāng)滾柱單邊最大變形量為0.01 mm時(shí)導(dǎo)向過渡曲面截型曲線 對(duì)比圖6與圖7可知,當(dāng)最大變形量改變時(shí)導(dǎo)向區(qū)曲線也隨之改變,但是最大值設(shè)定之后,導(dǎo)向曲線可適應(yīng)任何小于此變形量的狀態(tài),因此在進(jìn)行導(dǎo)向面設(shè)計(jì)時(shí)僅需設(shè)定滿足產(chǎn)品承受最大載荷(最大變形量)時(shí)的狀態(tài)即可。 圖7中曲線在長(zhǎng)度為5 mm的導(dǎo)向區(qū)域內(nèi)僅取了10個(gè)點(diǎn),實(shí)際生產(chǎn)應(yīng)用時(shí)無法滿足需要,需要推導(dǎo)出規(guī)律方程,方便數(shù)控系統(tǒng)控制數(shù)控機(jī)床對(duì)導(dǎo)向面進(jìn)行加工,根據(jù)圖8所示的數(shù)據(jù)利用MATLAB軟件中的Basic Fitting工具進(jìn)行曲線擬合,獲得式(7)。 通過擬合獲得的參數(shù)方程為 y=-0.000 42x3+0.004 3x2-0.016x+0.026 (7) 式(7)滿足圖7所示曲線的擬合的參數(shù)方程,由于軌道導(dǎo)向面截型與滾柱參數(shù)及軌道面無關(guān),僅與彈性變形量有關(guān),因此參數(shù)方程具有廣泛的適應(yīng)性,可滿足任意型號(hào)的滾柱進(jìn)出承載區(qū)軌道導(dǎo)向面的計(jì)算。根據(jù)圖8中擬合曲線的殘差圖可知曲線方程與原曲線切合度非常高,最大誤差不超過5%,可實(shí)現(xiàn)對(duì)原曲線的表述。 (a) 基于滾子等變形能導(dǎo)向過渡曲面截型曲線 當(dāng)滾動(dòng)體處于圖5所示的點(diǎn)(k1,k2,k3,…,kn)時(shí),彈性變形力如圖9所示,通過式(2)計(jì)算獲得,彈性變形量通過基于“等功”原理設(shè)計(jì)后獲得的每個(gè)點(diǎn)的縱坐標(biāo)δ1,δ2,δ3,…,δn為計(jì)算參量獲得。從圖9可知:隨著運(yùn)動(dòng)的進(jìn)行,受力越來越大,但是增加的幅度越來越小。 圖9 當(dāng)滾柱進(jìn)入承載區(qū)時(shí)滾子受力情況 由于滾動(dòng)接觸副的壽命受接觸應(yīng)力影響較大,因此需要對(duì)滾柱在導(dǎo)向區(qū)各點(diǎn)處的最大接觸應(yīng)力進(jìn)行校核,避免超過材料許用應(yīng)力的情況出現(xiàn)。 根據(jù)赫茲接觸理論可知接觸區(qū)最大接觸應(yīng)力計(jì)算公式為 (8) 式中,∑ρ為接觸副的曲率和。 由于導(dǎo)向曲面可根據(jù)通過擬合獲得的式(7)進(jìn)行表征,分別對(duì)式(7)進(jìn)行一次求導(dǎo)和二次求導(dǎo)得 (9) 根據(jù)曲線方程曲率計(jì)算公式及式(9)可得 (10) 根據(jù)式(10)可計(jì)算出導(dǎo)向面上的點(diǎn)k1,k2,k3,…,kn的曲率,結(jié)合接觸區(qū)最大應(yīng)力計(jì)算式式(8)對(duì)接觸應(yīng)力進(jìn)行計(jì)算,結(jié)果如圖10所示。 由圖9、圖10所示滾子進(jìn)入承載區(qū)時(shí)接觸力及接觸應(yīng)力的變化情況可知:最大接觸應(yīng)力遠(yuǎn)低于許用應(yīng)力值,可確保滾柱直線導(dǎo)軌副的壽命。 圖10 導(dǎo)向區(qū)內(nèi)滾動(dòng)體接觸應(yīng)力分布曲線 試驗(yàn)以LZG45型滾柱直線導(dǎo)軌副為試驗(yàn)品,軌道導(dǎo)向面分別按4種結(jié)構(gòu)形式進(jìn)行加工,即:直線型、圓弧形、“等剛度”型、及“等功”型,針對(duì)同型號(hào)、同批次產(chǎn)品分別加工4種類型的導(dǎo)向面,然后進(jìn)行滑塊運(yùn)動(dòng)振動(dòng)性能對(duì)比測(cè)試試驗(yàn),驗(yàn)證本文設(shè)計(jì)結(jié)構(gòu)的合理性及其對(duì)抑制振動(dòng)的效果。 試驗(yàn)用的滑塊取自同型號(hào)、同批次制造產(chǎn)品,不同類型軌道導(dǎo)向面均在同一臺(tái)高精密、數(shù)控磨床上制作完成,裝配后進(jìn)行運(yùn)動(dòng)振動(dòng)情況對(duì)比,其中直線型導(dǎo)向面傾斜角為0.1°,長(zhǎng)度為5 mm;圓弧型導(dǎo)向面半徑500 mm;“等剛度”型導(dǎo)向面尺寸按參考文獻(xiàn)中的相關(guān)計(jì)算原理設(shè)計(jì)制作,導(dǎo)向面長(zhǎng)度為5 mm;“等功”型導(dǎo)向面按1.2節(jié)推導(dǎo)的公式進(jìn)行設(shè)計(jì)制作;產(chǎn)品測(cè)試前進(jìn)行充分跑合,加工導(dǎo)向面之后的軌道端部結(jié)構(gòu)圖,如圖11所示。 圖11 滑塊軌道導(dǎo)向過渡區(qū)位置圖 滾柱導(dǎo)軌副振動(dòng)檢測(cè)原理及傳感器安裝方法,如圖12所示。待測(cè)工件及傳感器安裝,如圖13所示。導(dǎo)軌綜合性能試驗(yàn)臺(tái)整體結(jié)構(gòu)圖,如圖14所示。 圖13 滾柱直線導(dǎo)軌副及傳感器安裝圖 圖14 振動(dòng)信號(hào)采集及分析系統(tǒng) 試驗(yàn)時(shí)使用INV9822A型振動(dòng)數(shù)據(jù)采集器對(duì)滑塊振動(dòng)情況進(jìn)行檢測(cè),信號(hào)采集儀使用東方振動(dòng)和噪聲技術(shù)研究所的INV3018C信號(hào)采集儀(8通道24位),分析軟件采用DASP V10振動(dòng)模態(tài)分析軟件。 圖15 滾動(dòng)直線導(dǎo)軌副可靠性試驗(yàn)臺(tái) 試驗(yàn)參數(shù)設(shè)定如表1所示。測(cè)試結(jié)果,如圖16~圖20所示。 (a) 滾柱直線導(dǎo)軌副垂直方向振動(dòng) 表1 滑塊軌道對(duì)滑塊運(yùn)動(dòng)振動(dòng)的影響試驗(yàn)參數(shù)表 (a) 滾柱直線導(dǎo)軌副垂直方向振動(dòng) (a) 滾柱直線導(dǎo)軌副垂直方向振動(dòng) (a) 滾柱直線導(dǎo)軌副垂直方向振動(dòng) (a) 滾柱直線導(dǎo)軌副垂直方向振動(dòng) 通過對(duì)比試驗(yàn)結(jié)果可知,與不帶導(dǎo)向面的滑塊振動(dòng)振幅相比帶導(dǎo)向過渡的滑塊振動(dòng)降低50%,導(dǎo)向面對(duì)改善滑塊運(yùn)動(dòng)振動(dòng)的效果非常明顯。 對(duì)比直線型、圓弧型、“等剛度”型和“等功”型導(dǎo)向面滑塊的振動(dòng)情況,雖然整體變化不超過6%~10%,具有“等功”型導(dǎo)向面的滑塊運(yùn)動(dòng)振動(dòng)幅值最小,基本實(shí)現(xiàn)優(yōu)化設(shè)計(jì)目標(biāo)。 通過對(duì)比圖21、圖22基于“等剛度”型導(dǎo)向面及“等功”型導(dǎo)向面的滑塊運(yùn)動(dòng)振動(dòng)情況可知:低速時(shí)相差不大,高速狀態(tài)時(shí)振動(dòng)明顯增大,且負(fù)載越大振動(dòng)越明顯,對(duì)比試驗(yàn)時(shí)“等剛度”型導(dǎo)向面的加工與其他形式的導(dǎo)向面采用同一設(shè)備進(jìn)行,在加工曲線的設(shè)定上依照參考文獻(xiàn)進(jìn)行,可能會(huì)存在對(duì)計(jì)算方法理解不足的問題[12-15]。 圖21 4 m/min速度條件下“等剛度”與“等功”型導(dǎo)向面滑塊振動(dòng)對(duì)比曲線 圖22 52 m/min速度條件下“等剛度”與“等功”型導(dǎo)向面滑塊振動(dòng)對(duì)比曲線 使用本文設(shè)計(jì)的導(dǎo)向面產(chǎn)品與不帶導(dǎo)向面產(chǎn)品的試驗(yàn)結(jié)構(gòu),如表2所示。從表2可知:“等功”型導(dǎo)向面的存在極大的提高產(chǎn)品的壽命,滾動(dòng)體與導(dǎo)向面的接觸疲勞極限,提升一個(gè)數(shù)量級(jí)。 表2 導(dǎo)向面改進(jìn)前、后產(chǎn)品壽命對(duì)比 采用DHL050型號(hào)的力錘傳感器對(duì)滑塊進(jìn)行激振,采用INV9822A型號(hào)的加速度傳感器(適用測(cè)量頻率比較高的機(jī)械結(jié)構(gòu))拾振。信號(hào)采集儀是東方振動(dòng)和噪聲技術(shù)研究所的INV3018C信號(hào)采集儀(8通道24位),模態(tài)分析軟件采用DASP V10模態(tài)分析軟件。模態(tài)試驗(yàn)現(xiàn)場(chǎng)裝置,如圖23所示。 圖23 模態(tài)試驗(yàn)測(cè)量裝置 在模態(tài)試驗(yàn)激勵(lì)時(shí)采用多點(diǎn)激勵(lì)單點(diǎn)輸出的方式進(jìn)行測(cè)量,傳感器固定位置不變,力錘敲擊所有的測(cè)點(diǎn)。并且在力錘敲擊時(shí)應(yīng)注意脈沖為單脈沖,避免試件與力錘的回?fù)簟y(cè)點(diǎn)的布置應(yīng)遠(yuǎn)離模態(tài)的節(jié)點(diǎn),這樣在測(cè)量時(shí)方便敲擊,又不丟失每個(gè)模態(tài)。滑塊測(cè)點(diǎn)的分布,如圖24所示。滑塊上表面分布9個(gè)測(cè)點(diǎn),每個(gè)測(cè)點(diǎn)均測(cè)量3次取平均值,來提高測(cè)量的精度。 圖24 錘擊測(cè)點(diǎn)分布圖 分別對(duì)基于“等剛度”型導(dǎo)向面及“等功”型導(dǎo)向面的滑塊組成的JSA-LZG45型滾柱直線導(dǎo)軌副頻率進(jìn)行模態(tài)試驗(yàn),試驗(yàn)時(shí)采用相同等級(jí)預(yù)緊力(輕預(yù)緊),相同潤(rùn)滑油(32號(hào)機(jī)械油)。 由于試驗(yàn)條件的限制,只能承受單軸激勵(lì)與振動(dòng)。模態(tài)試驗(yàn)是根據(jù)一階、二階設(shè)計(jì)的,測(cè)點(diǎn)的布置也是圍繞前兩階模態(tài)設(shè)置。由于傳感器和環(huán)境干擾等因素,三階及以上的頻率誤差特別大,失真嚴(yán)重,結(jié)果只取前兩階。一階振型為繞y軸轉(zhuǎn)動(dòng)(俯仰),二階振型沿z軸上下移動(dòng)(上下)。為減小誤差,每根導(dǎo)軌副測(cè)量3次取均值,試驗(yàn)結(jié)果,如表3所示。從表3可知:基于“等功”型導(dǎo)向面滑塊滾柱直線導(dǎo)軌副其兩階固有頻率均比基于“等剛度”型導(dǎo)向面滑塊的導(dǎo)軌副固有頻率高,但差別不大。 表3 不同導(dǎo)向面滑塊的導(dǎo)軌副模態(tài)試驗(yàn)結(jié)果 為驗(yàn)證預(yù)緊力對(duì)導(dǎo)軌副固有頻率的影響,分別對(duì)采用輕預(yù)緊(0.02C)、中預(yù)緊(0.05C)和重預(yù)緊(0.08C)3種預(yù)緊等級(jí)的導(dǎo)軌副進(jìn)行模態(tài)試驗(yàn),在相同試驗(yàn)條件下進(jìn)行模態(tài)試驗(yàn)測(cè)試,試驗(yàn)結(jié)果如表4所示。 表4 不同預(yù)緊力等級(jí)導(dǎo)軌副模態(tài)試驗(yàn)結(jié)果 從表4可知:導(dǎo)軌副預(yù)緊力越大,其固有頻率越大,但變化幅度越小。 (1) 以滾動(dòng)體進(jìn)入承載區(qū)形變的時(shí)間歷程為主線,建立基于“等功”原理的導(dǎo)向面計(jì)算模型,通過MATLAB軟件計(jì)算獲得導(dǎo)向面截型的離散點(diǎn)位圖,并擬合出截面的曲線方程,并對(duì)滾動(dòng)體進(jìn)、出通過導(dǎo)向面的接觸力及接觸應(yīng)力進(jìn)行了校核。 (2) 軌道導(dǎo)向面對(duì)降低滑塊運(yùn)動(dòng)振動(dòng)效果非常明顯,在高精度、高速、重載使用環(huán)境的滾柱直線導(dǎo)軌副都需要在滑塊的端部設(shè)置導(dǎo)向面結(jié)構(gòu)。 (3) 直線型、圓弧型、“等剛度”型及本文建立的“等功”型軌道導(dǎo)向面結(jié)構(gòu)對(duì)滾柱直線導(dǎo)軌副的振動(dòng)都具有一定的抑制效果,相比較而言“等功”型的導(dǎo)向面對(duì)滑塊振動(dòng)及其運(yùn)動(dòng)噪聲的抑制效果最好。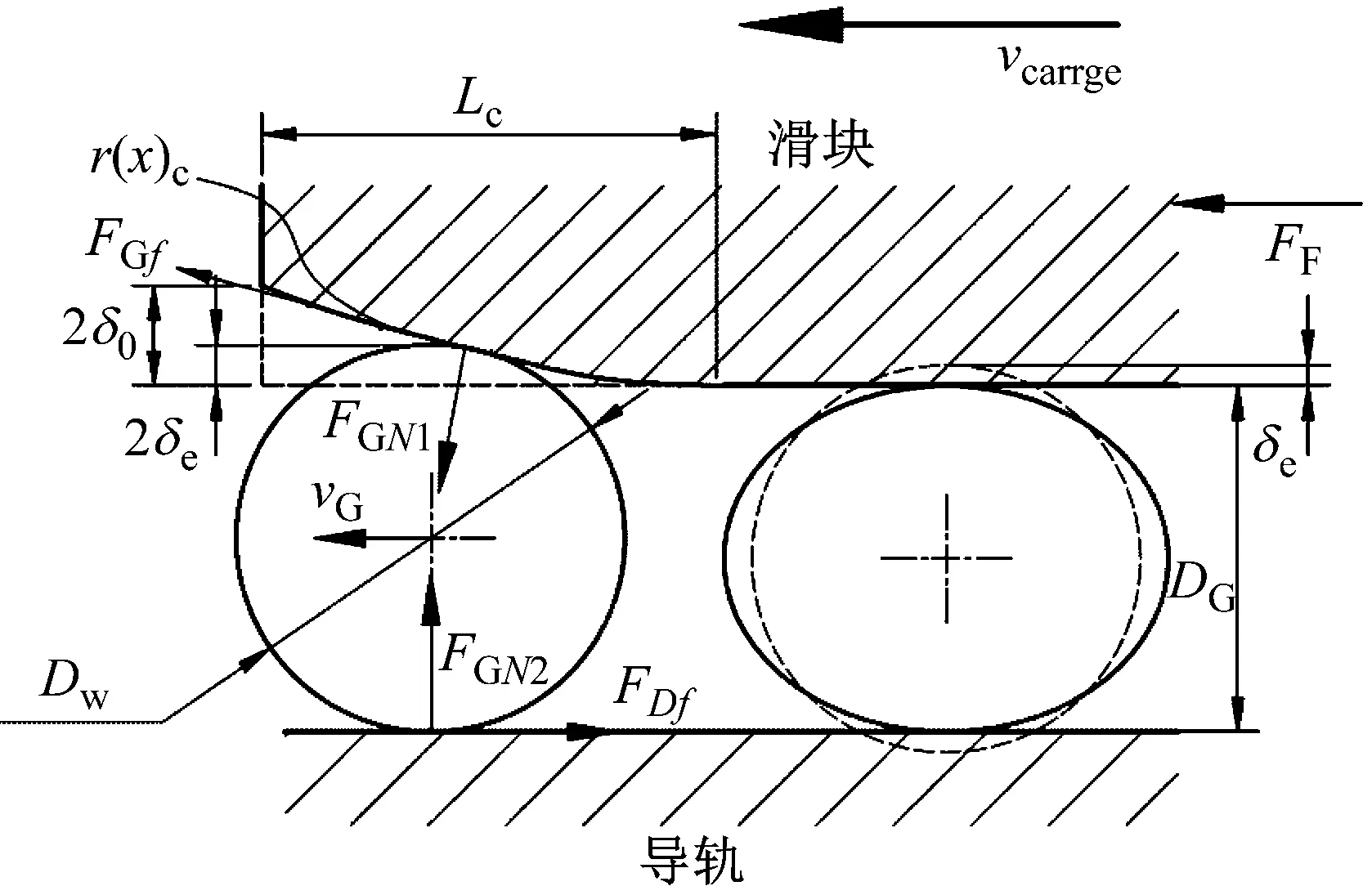

1.2 基于“等功”原理導(dǎo)向過渡面截型方程的建立
1.3 導(dǎo)向區(qū)接觸力及接觸應(yīng)力驗(yàn)證
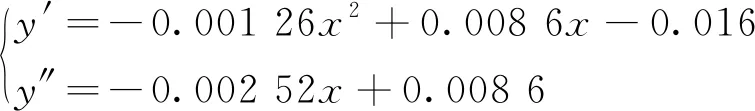
2 “等功”型軌道導(dǎo)向面振動(dòng)性能測(cè)試及試驗(yàn)分析
2.1 試驗(yàn)原理及裝置




2.2 滑塊運(yùn)動(dòng)振動(dòng)對(duì)比試驗(yàn)過程及試驗(yàn)數(shù)據(jù)分析

3 滾柱直線導(dǎo)軌副模態(tài)試驗(yàn)研究
3.1 試驗(yàn)介紹


3.2 試驗(yàn)結(jié)果

4 結(jié) 論

