基于SKF-KF-Bayes的滾動(dòng)軸承剩余使用壽命預(yù)測(cè)方法
許艷雷, 邱 明,2, 李軍星,2, 劉 璐, 牛凱岑
(1.河南科技大學(xué) 機(jī)械工程學(xué)院,河南 洛陽(yáng) 471003;2.河南科技大學(xué) 高端軸承先進(jìn)制造與智能裝備河南省工程技術(shù)研究中心,河南 洛陽(yáng) 471003)
滾動(dòng)軸承廣泛應(yīng)用于旋轉(zhuǎn)機(jī)械中,是決定機(jī)械設(shè)備安全可靠運(yùn)行的關(guān)鍵部件之一,一旦發(fā)生失效,設(shè)備無(wú)法正常工作,甚至?xí)斐删薮蟮慕?jīng)濟(jì)損失和人員傷亡。開(kāi)展?jié)L動(dòng)軸承剩余使用壽命(remaining useful life,RUL)預(yù)測(cè),對(duì)于保證機(jī)械設(shè)備安全可靠運(yùn)行、提高設(shè)備的生產(chǎn)效率具有重要的意義[1-2]。
根據(jù)Vichare等[3]的研究,機(jī)械設(shè)備RUL預(yù)測(cè)方法可分為兩類:基于失效物理模型的RUL預(yù)測(cè)和基于數(shù)據(jù)驅(qū)動(dòng)的RUL預(yù)測(cè)方法。基于失效物理的RUL預(yù)測(cè)較準(zhǔn)確,但隨著科技的進(jìn)步,設(shè)備的復(fù)雜性也在增加,其退化機(jī)理涉及多個(gè)學(xué)科的知識(shí),建立物理退化模型十分困難;基于數(shù)據(jù)驅(qū)動(dòng)的RUL預(yù)測(cè)不需要建立退化機(jī)理模型,只需要實(shí)時(shí)監(jiān)測(cè)產(chǎn)品的退化數(shù)據(jù),對(duì)于復(fù)雜的機(jī)械設(shè)備較為實(shí)用。基于數(shù)據(jù)驅(qū)動(dòng)的RUL預(yù)測(cè)包括基于機(jī)器學(xué)習(xí)的RUL預(yù)測(cè)和基于統(tǒng)計(jì)數(shù)據(jù)驅(qū)動(dòng)的RUL預(yù)測(cè)[4]。
滾動(dòng)軸承的退化包括明顯的平穩(wěn)退化和加速退化。在平穩(wěn)退化階段,滾動(dòng)軸承的各項(xiàng)性能指標(biāo)不會(huì)有明顯的變化,發(fā)生早期故障后,隨著工作時(shí)間的持續(xù),其性能退化逐漸加劇,直到退化量達(dá)到閾值失效。張繼冬等[5]基于全層卷積神經(jīng)網(wǎng)絡(luò)進(jìn)行軸承壽命預(yù)測(cè),并采用加權(quán)平均法對(duì)結(jié)果進(jìn)行降噪處理。Elforjani[6]提出了一個(gè)線性回歸分類器和多層人工神經(jīng)網(wǎng)絡(luò)模型,通過(guò)聯(lián)系聲發(fā)射特征與軸承磨損來(lái)估算軸承的RUL。于震梁等[7]提出一種將支持向量機(jī)與非線性卡爾曼濾波相結(jié)合的RUL預(yù)測(cè)模型,計(jì)算各個(gè)時(shí)刻RUL的估計(jì)值及一定的置信區(qū)間。張龍龍[8]發(fā)現(xiàn)希爾伯特熵可以較好地分辨軸承的衰退處于哪個(gè)階段,并且利用支持向量機(jī)(support vector machine, SVM)建立了預(yù)測(cè)模型。孫磊等[9]提出一種基于粒子濾波理論的設(shè)備RUL預(yù)測(cè)方法,解決非線性非高斯系統(tǒng)的RUL預(yù)測(cè)問(wèn)題。文娟等[10]針對(duì)粒子濾波中粒子退化提出一種基于無(wú)跡粒子濾波算法的軸承RUL預(yù)測(cè)方法。Peng等[11]利用伽馬過(guò)程處理產(chǎn)品的退化過(guò)程,采用Bayes方法進(jìn)行參數(shù)估計(jì)和退化分析,預(yù)測(cè)產(chǎn)品的RUL。Pan等[12]采用具有隨機(jī)效應(yīng)的逆高斯過(guò)程來(lái)表征系統(tǒng)的退化過(guò)程。然后利用期望最大化算法對(duì)模型參數(shù)進(jìn)行估計(jì),并利用Bayes方法對(duì)退化模型中的隨機(jī)參數(shù)進(jìn)行更新,使得估計(jì)的RUL能夠根據(jù)新的退化數(shù)據(jù)進(jìn)行實(shí)時(shí)更新。Lu等[13]將Bayes理論應(yīng)用于估計(jì)設(shè)備的RUL分布。Gebraeel等[14]在Lu等的基礎(chǔ)上,利用包含布朗運(yùn)動(dòng)誤差的指數(shù)模型擬合滾動(dòng)軸承的退化軌跡,在Bayes定理的框架下更新模型參數(shù),從而實(shí)現(xiàn)了RUL的預(yù)測(cè)。Wang等[15-16]改進(jìn)Gebraee提出的模型預(yù)測(cè)機(jī)械設(shè)備的RUL。
然而上述RUL預(yù)測(cè)方法存在各自的不足,機(jī)器學(xué)習(xí)不僅透明度低,還需要大量高質(zhì)量的訓(xùn)練數(shù)據(jù),而這些數(shù)據(jù)在生產(chǎn)實(shí)際中很難獲取,與神經(jīng)網(wǎng)絡(luò)相比,SVM在處理小樣本量問(wèn)題上更有優(yōu)勢(shì),但目前SVM的參數(shù)和核函數(shù)的確定有很大的困難;粒子濾波算法同樣需要大量的數(shù)據(jù)才能進(jìn)行準(zhǔn)確預(yù)測(cè);逆高斯過(guò)程模型與伽馬過(guò)程模型局限于馬爾可夫性質(zhì)和單調(diào)過(guò)程;由于滾動(dòng)軸承退化具有明顯的階段性,如果直接利用指數(shù)函數(shù)對(duì)全壽命試驗(yàn)數(shù)據(jù)模擬可能會(huì)造成較大的偏差,為了提高預(yù)測(cè)精度,準(zhǔn)確區(qū)分滾動(dòng)軸承退化狀態(tài)是十分必要的。
針對(duì)上述①如何準(zhǔn)確有效區(qū)分滾動(dòng)軸承退化階段;②如何在有限數(shù)據(jù)集中有效結(jié)合同類軸承退化數(shù)據(jù)與待預(yù)測(cè)軸承實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)。本文提出一種SKF(switching Kalman filters)-KF(Kalman filters)-Bayes相結(jié)合的滾動(dòng)軸承RUL預(yù)測(cè)方法。SKF不需要設(shè)置軸承進(jìn)入加速退化階段的閾值根據(jù)軸承實(shí)時(shí)監(jiān)測(cè)振動(dòng)信號(hào)自適應(yīng)判斷軸承退化狀態(tài);KF狀態(tài)方程的確定需要同類滾動(dòng)軸承全壽命周期的監(jiān)測(cè)數(shù)據(jù),Bayes預(yù)測(cè)時(shí)考慮待預(yù)測(cè)軸承的實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù),有效結(jié)合了現(xiàn)有的數(shù)據(jù)和實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)。
本文主要包括滾動(dòng)軸承退化狀態(tài)判斷和RUL預(yù)測(cè)。在退化階段的判斷部分,根據(jù)滾動(dòng)軸承均方根利用SKF判斷各個(gè)時(shí)刻所處的退化階段,處于平穩(wěn)階段的滾動(dòng)軸承健康狀態(tài)良好不進(jìn)行RUL預(yù)測(cè)。當(dāng)退化處于加速階段時(shí),利用包含布朗運(yùn)動(dòng)誤差的指數(shù)模型描述滾動(dòng)軸承的退化,根據(jù)KF單步預(yù)測(cè)對(duì)實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)進(jìn)行修正繼而利用Bayes更新模型參數(shù),確定RUL概率密度函數(shù)估計(jì)滾動(dòng)軸承的RUL。SKF不需要設(shè)置軸承進(jìn)入加速退化階段的閾值根據(jù)軸承實(shí)時(shí)監(jiān)測(cè)信號(hào)自適應(yīng)判斷軸承退化狀態(tài);隨機(jī)效應(yīng)指數(shù)模型的使用減少了對(duì)高質(zhì)量數(shù)據(jù)的依賴;KF單步預(yù)測(cè)減少實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)的隨機(jī)性,有效提高了滾動(dòng)軸承RUL預(yù)測(cè)的精度;Bayes方法更新模型參數(shù),減少長(zhǎng)期預(yù)測(cè)的不確定性。本文不依賴大量高質(zhì)量數(shù)據(jù)和精確的物理模型實(shí)現(xiàn)了滾動(dòng)軸承RUL的準(zhǔn)確預(yù)測(cè)。
1 問(wèn)題描述
滾動(dòng)軸承的退化是非平穩(wěn)的,如圖1所示。即滾動(dòng)軸承各個(gè)退化階段的退化模型是不同的;退化的變點(diǎn)是隨機(jī)的,即滾動(dòng)軸承進(jìn)入加速退化階段的時(shí)刻也是不同的。準(zhǔn)確識(shí)別滾動(dòng)軸承進(jìn)入加速退化階段的變點(diǎn),可以提高性能退化建模和RUL預(yù)測(cè)的精度。
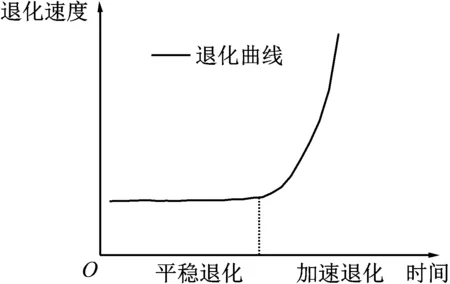
圖1 滾動(dòng)軸承性能退化圖
2 滾動(dòng)軸承性能退化建模
2.1 變點(diǎn)識(shí)別方法
本文將滾動(dòng)軸承的退化分為平穩(wěn)退化和加速退化兩個(gè)階段。由于滾動(dòng)軸承的差異性,其振動(dòng)信號(hào)不盡相同,當(dāng)進(jìn)入加速退化階段時(shí),均方根的變化也存在差異,SKF可以跟蹤滾動(dòng)軸承退化過(guò)程的動(dòng)態(tài)變化,不需要大量的數(shù)據(jù)訓(xùn)練模型,自適應(yīng)獲得各時(shí)刻最可能的退化模型。SKF由多個(gè)線性狀態(tài)空間模型組成,也被稱為線性動(dòng)態(tài)模型[17]或交互多模型[18]。
SKF可以被表示為一個(gè)動(dòng)態(tài)Bayes網(wǎng)絡(luò),如圖2所示。每個(gè)動(dòng)態(tài)模型St都可以表示為一個(gè)基本KF。為確定各個(gè)時(shí)刻所處的退化階段,從均方根觀測(cè)值yt中推斷出模型概率St和模型狀態(tài)xt。
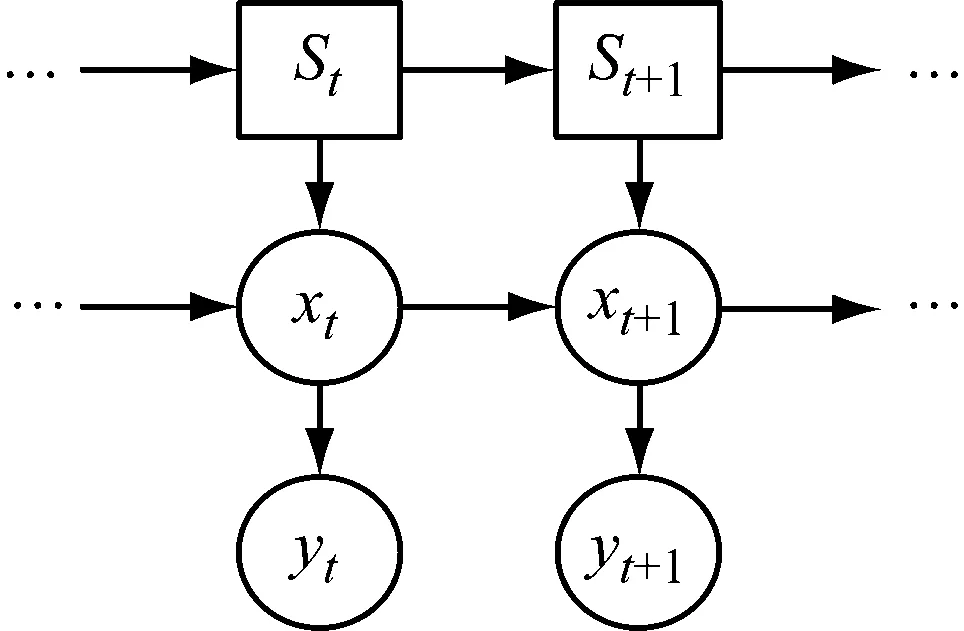
圖2 SKF的動(dòng)態(tài)Bayes表示
卡爾曼濾波的預(yù)測(cè)及更新過(guò)程如下。
預(yù)測(cè):
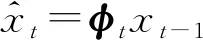
(1)
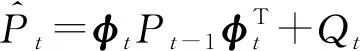
(2)
更新:
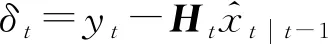
(3)
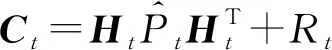
(4)
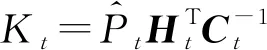
(5)
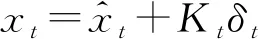
(6)
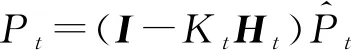
(7)
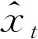
本文將滾動(dòng)軸承的退化過(guò)程分為平穩(wěn)退化和加速退化,即SKF中包括兩個(gè)基本KF。模型轉(zhuǎn)移概率Zij為權(quán)重,并在加權(quán)概率之和上進(jìn)行歸一化。
從測(cè)量殘差考慮每個(gè)濾波器的可能性
(8)
各模型的概率
(9)
狀態(tài)加權(quán)
(10)
協(xié)方差加權(quán)
(11)
利用狀態(tài)和協(xié)方差加權(quán)估計(jì),通過(guò)式(1)~式(7)對(duì)兩個(gè)基本的KF進(jìn)行預(yù)測(cè),每個(gè)濾波器都產(chǎn)生一個(gè)預(yù)測(cè)狀態(tài)x和協(xié)方差p估計(jì)值,然后利用式(8)確定每個(gè)濾波器的可能性,得到各模型在當(dāng)前時(shí)刻的概率式(9),從而確定各個(gè)時(shí)刻滾動(dòng)軸承的退化狀態(tài)。在Lim等的研究中有關(guān)于SKF的詳細(xì)介紹。
2.2 退化建模
從圖1可知,當(dāng)滾動(dòng)軸承進(jìn)入加速退化階段后,其退化趨勢(shì)接近指數(shù)模型,令Y(t)為滾動(dòng)軸承均方根退化過(guò)程。本文假設(shè)Y(t)的函數(shù)表達(dá)式為
(12)
為計(jì)算方便,將式(12)取對(duì)數(shù)變形為
LY(t)=ln[Y(t)-α]=
θ′+β′t+ε(t)
(13)
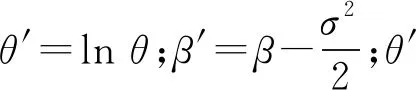
由已經(jīng)監(jiān)測(cè)到的滾動(dòng)軸承均方根LY(1),LY(2),…,LY(ti),本文中定義
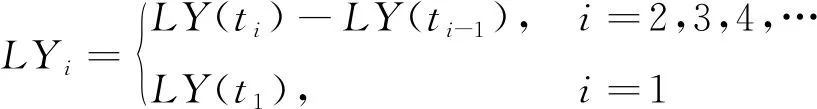
2.3 模型參數(shù)估計(jì)
2.3.1 初始參數(shù)估計(jì)
2.3.2 后驗(yàn)參數(shù)估計(jì)
根據(jù)監(jiān)測(cè)數(shù)據(jù)LY(1),LY(2),…,LY(tk),由Bayes定理得θ′和β′的后驗(yàn)分布參數(shù)為
μθ′=
(14)
μβ′=
(15)
(16)
(17)
3 滾動(dòng)軸承RUL預(yù)測(cè)
3.1 修正實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)
在滾動(dòng)軸承振動(dòng)信號(hào)測(cè)量的過(guò)程中不可避免會(huì)受到外界的影響,進(jìn)而導(dǎo)致Bayes更新結(jié)果的不準(zhǔn)確。利用KF單步預(yù)測(cè)對(duì)滾動(dòng)軸承實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)進(jìn)行修正,減少數(shù)據(jù)的隨機(jī)性提高壽命預(yù)測(cè)的精度。
對(duì)數(shù)據(jù)進(jìn)行對(duì)數(shù)線性化處理,根據(jù)式(1)~式(7)對(duì)滾動(dòng)軸承實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)進(jìn)行KF單步預(yù)測(cè),KF單步預(yù)測(cè)的狀態(tài)方程為
L=a+b·t+ε(t)
(18)
式中:a為同類軸承退化數(shù)據(jù)平穩(wěn)退化階段特征值的均值;b為同類軸承退化數(shù)據(jù)加速退化階段特征值增量的均值,誤差項(xiàng)的計(jì)算見(jiàn)2.3.1節(jié)。
3.2 RUL分布模型
根據(jù)監(jiān)測(cè)數(shù)據(jù)LY1,LY2,…,LYk,LY(t+tk)為一個(gè)正態(tài)隨機(jī)變量,當(dāng)LY(T+tk)=D時(shí)判斷滾動(dòng)軸承失效,T為滾動(dòng)軸承的RUL,D為失效閾值。T的累積分布函數(shù)為
(19)
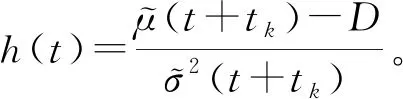
根據(jù)監(jiān)測(cè)數(shù)據(jù),LY1,LY2,…,LYk,LY(t+tk)為一個(gè)正態(tài)隨機(jī)變量且
(20)
(21)
由式(19)可以得到滾動(dòng)軸承RUL的概率密度函數(shù)
fT|LY1,LY2,…,LYk,T>0(t)=φ[h(t)]h′(t)
(22)
4 工程實(shí)例
利用實(shí)際試驗(yàn)中獲得的滾動(dòng)軸承全壽命周期振動(dòng)信號(hào)驗(yàn)證本文所提方法的有效性。本文所采用的數(shù)據(jù)集XJTU-SY[19]是由西安交通大學(xué)設(shè)計(jì)科學(xué)與基礎(chǔ)構(gòu)件研究所和浙江長(zhǎng)興昇陽(yáng)科技股份有限公司提供。試驗(yàn)機(jī)結(jié)構(gòu),如圖3所示。試驗(yàn)軸承的型號(hào)為L(zhǎng)DK UER204;選取載荷p和速度v為加速應(yīng)力,在3種工況條件下對(duì)滾動(dòng)軸承進(jìn)行試驗(yàn),每個(gè)工況下試驗(yàn)5個(gè)軸承,工況條件如表1所示。試驗(yàn)中水平和垂直方向的PCB 352C33單向加速度傳感器同時(shí)采集信號(hào),采樣頻率為25.6 kHz,每1 min采集1.28 s的振動(dòng)信號(hào)[20]。
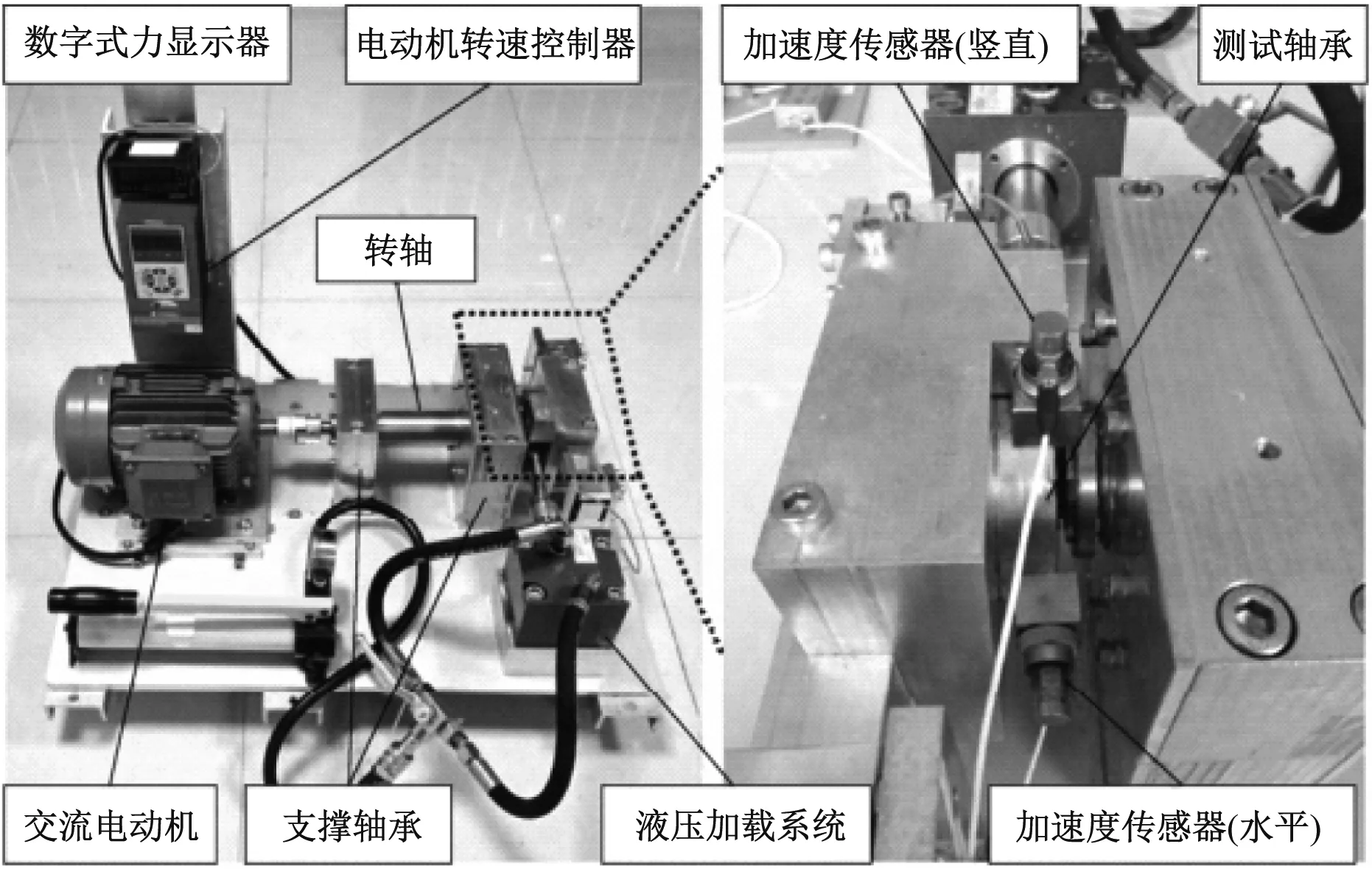
(a) 試驗(yàn)機(jī)整體圖 (b) 局部放大圖

表1 滾動(dòng)軸承試驗(yàn)工況表
計(jì)算各個(gè)試驗(yàn)滾動(dòng)軸承水平方向振動(dòng)信號(hào)的均方根值,對(duì)均方根數(shù)據(jù)進(jìn)行滑移平均處理,利用SKF判斷工況2軸承各時(shí)刻退化狀態(tài),如圖4所示。圖4中:退化狀態(tài)1表示軸承處于平穩(wěn)退化;退化狀態(tài)2表示軸承處于加速退化。由于振動(dòng)信號(hào)的隨機(jī)性和測(cè)量誤差的影響,均方根的退化過(guò)程不是單調(diào)遞增的,此時(shí)SKF模型識(shí)別軸承退化狀態(tài)的能力減弱,本文中定義滾動(dòng)軸承連續(xù)5個(gè)或5個(gè)以上時(shí)刻的退化狀態(tài)處于加速退化時(shí),該滾動(dòng)軸承進(jìn)入加速退化階段。對(duì)均方根數(shù)據(jù)進(jìn)行滑移平均處理后,利用SKF判斷工況2條件下各個(gè)滾動(dòng)軸承進(jìn)入加速退化階段的時(shí)刻,如表2所示。
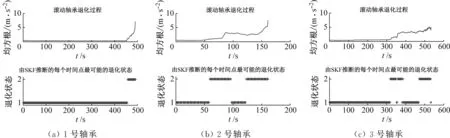
圖4 工況2軸承退化軌跡及各時(shí)刻最可能的退化狀態(tài)

表2 各軸承進(jìn)入加速退化階段時(shí)刻表
本文利用工況2下2號(hào)、3號(hào)、4號(hào)、5號(hào)軸承的均方根退化數(shù)據(jù)預(yù)測(cè)工況2下1號(hào)軸承的RUL。根據(jù)表2獲得各軸承進(jìn)入加速退化階段的時(shí)刻,利用包含布朗運(yùn)動(dòng)誤差的指數(shù)模型式(13)擬合滾動(dòng)軸承進(jìn)入加速退化階段后的均方根退化軌跡,各軸承退化軌跡參數(shù),如表3所示。

表3 軸承退化模型參數(shù)表
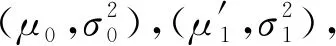

表4 先驗(yàn)分布參數(shù)表
利用KF對(duì)實(shí)時(shí)監(jiān)測(cè)到的振動(dòng)信號(hào)進(jìn)行單步預(yù)測(cè),根據(jù)KF單步預(yù)測(cè)結(jié)果和先驗(yàn)分布參數(shù)利用式(14)~式(17)得工況2下1號(hào)軸承的后驗(yàn)分布參數(shù),繼而根據(jù)式(20)~式(22)得到工況2下1號(hào)軸承RUL的概率密度函數(shù)。本文中確定滾動(dòng)軸承的失效閾值為其他4個(gè)軸承失效閾值的平均值,概率密度函數(shù)的最高點(diǎn)為RUL的估計(jì)值。為了說(shuō)明本文提出方法的有效性,將本文所提方法與Bayes,相關(guān)向量機(jī)(relevance vector machine,RVM)預(yù)測(cè)滾動(dòng)軸承RUL的方法進(jìn)行了對(duì)比,得到對(duì)比結(jié)果,如圖5所示。
從圖5可知,在同樣的數(shù)據(jù)樣本下,本文所提預(yù)測(cè)滾動(dòng)軸承RUL方法的準(zhǔn)確度要遠(yuǎn)遠(yuǎn)高于RVM方法,這是因?yàn)镽VM同SVM一樣對(duì)參數(shù)和核函數(shù)有很大的依賴性,但目前比較成熟的核函數(shù)及其參數(shù)的選擇都是根據(jù)經(jīng)驗(yàn)來(lái)選取的,帶有一定的隨意性;本文所提方法有效地減少了實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù)的隨機(jī)性,降低了外界環(huán)境對(duì)Bayes更新的影響,并且隨著預(yù)測(cè)時(shí)間的增加預(yù)測(cè)精度也在逐漸增大。
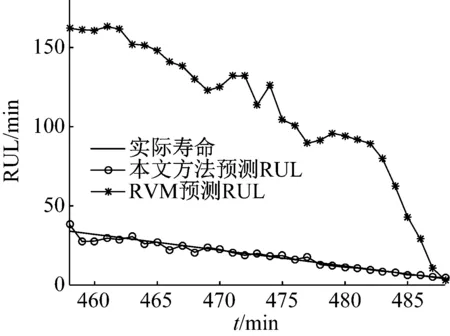
(a) 本文方法與RVM對(duì)比
5 結(jié) 論
針對(duì)滾動(dòng)軸承壽命預(yù)測(cè)中存在的兩個(gè)問(wèn)題:準(zhǔn)確區(qū)分滾動(dòng)軸承退化階段和有效地利用歷史退化數(shù)據(jù)與實(shí)時(shí)監(jiān)測(cè)數(shù)據(jù),本文提出一種基于SKF-KF-Bayes理論的滾動(dòng)軸承性能退化建模與RUL預(yù)測(cè)方法。其特點(diǎn)在于① SKF根據(jù)軸承實(shí)時(shí)監(jiān)測(cè)振動(dòng)信號(hào)自適應(yīng)判斷軸承退化狀態(tài)且不需要設(shè)置進(jìn)入加速退化階段的閾值;② KF單步預(yù)測(cè)有效減少了實(shí)時(shí)振動(dòng)監(jiān)測(cè)數(shù)據(jù)的隨機(jī)性;③ Bayes方法更新模型參數(shù),減少了滾動(dòng)軸承RUL長(zhǎng)期預(yù)測(cè)的不確定性。通過(guò)滾動(dòng)軸承實(shí)例分析,驗(yàn)證本文提出方法不依賴大量高質(zhì)量數(shù)據(jù)實(shí)現(xiàn)了滾動(dòng)軸承RUL的準(zhǔn)確預(yù)測(cè)。

