基于wMPS測量剛性結構振動頻率的可行性研究

熊春寶， 白洪志， 王 猛

(天津大學 建筑工程學院，天津 300072)

近年來，許多學者一直研究通過自動全站儀(robotic total stations,RTS)和全球衛星導航系統(global navigation satellite system，GNSS)等大地測量傳感器監測半靜態和動態大型工程結構(如高層建筑、大跨度橋梁等)的位移與變形[1-6]。這種對結構性能進行實時監測的方法，除了能及時發現結構的損傷之外，還能通過安全性能評估預測其性能進一步變化，使維護人員提前做出維護決定，這對提高結構的安全性能有著重要的意義，已經成為評定現代工程健康運行的硬性指標。但是，對于測量剛性結構(頻率大于1 Hz，振幅小于1 cm)的固有參數，如人行天橋等的變形[7-10]給現階段的測量儀器帶來了巨大挑戰。如：RTS無法進行并行測量，且實際采樣頻率只有6～7 Hz(額定采用頻率10 Hz)；GNSS雖能進行并行測量，但因衛星信號等內外部因素的影響導致其動態測量精度受到限制，且只能測量振幅在5 mm以上的結構振動[11]，當測量剛性結構時其優勢明顯降低。

工作空間定位系統(workspace measurement positioning system，wMPS)是基于光電掃描的新型網絡式大尺寸三維坐標測量系統，具有量程覆蓋大、測量精度高、測量頻率高、可實現多任務同步測量等優勢,已成為當前工業界和學術界的關注熱點。其中，Yang等[12]提出了具體的實現方案及標定方法，分析了系統的主要誤差來源及影響；Duanmu等[13]從硬件層面對wMPS的電氣結構進行了優化設計，為wMPS系統實現動態坐標測量提供了理論基礎；Geng等[14]利用蒙特卡洛仿真研究了wMPS的空間測角誤差，設計了系統的角度校準裝置，提出測量誤差的補償方法；Xiong等[15]分析了wMPS多種典型網絡布局方案與定位誤差的關系，并結合wMPS特性提出了一種最優網絡布局策略；Zhao等[16]建立系統動態測量誤差模型，以此為基礎通過多發射站間同步誤差補償和采用卡爾曼濾波模型來減小系統動態測量誤差，并用試驗進行了驗證。

wMPS較高的測量精度和優秀的動態測量性能，使得該系統非常適合于結構的健康監測，補充RTS與GNSS在測量剛性結構固有參數時的劣勢。為了驗證這種可行性，采取逆向工程法進行試驗，用最小二乘擬合的方法定義了X軸，通過快速傅里葉變換(fast Fourier transform，FFT)分析時間序列數據，驗證wMPS測量結構固有參數的可行性，并給出可以獲取振動主頻率的最大值，為后續應用提供了必要基礎。

1 wMPS系統測量的基本原理

wMPS系統由發射站、接收器和計算機相連。發射站由上部的轉動頭和下部的基座組成,如圖1所示。

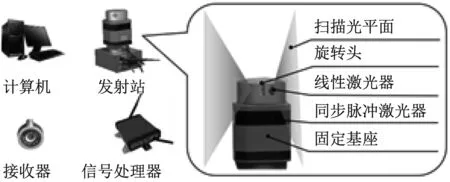
圖1 wMPS測量系統

轉動頭上安裝有兩個激光器，二者在水平旋轉方向上間隔90°，激光器能發射扇面狀的激光，兩激光扇面與水平面成60°夾角，基座上安裝有一個同步脈沖激光器。系統工作時，旋轉頭繞著固定軸沿著逆時針方向勻速旋轉，兩個線性激光器在空間四周進行連續激光掃描，當轉子轉至初始位置時，基座上的同步脈沖發射器發射一圈同步光信號并開始計時。當任意扇形激光平面掃過接收器時，通過計數脈沖可以得到該平面從初始位置轉至接收器位置時的旋轉角度。利用同樣的方法，當空間內的所有激光平面都掃過同一接收器時，可以建立基于多平面約束的約束方程，從而求出接收器處的坐標。

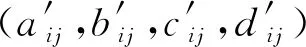
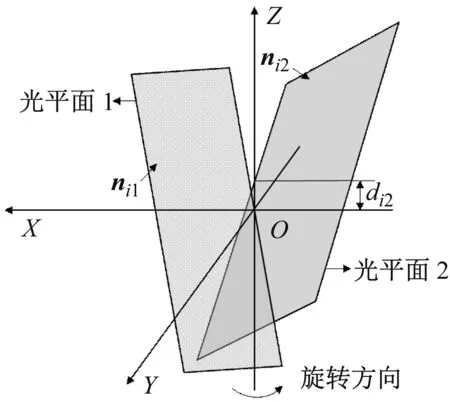
圖2 測量坐標系示意圖

(1)

(2)

式中，θj為兩個光平面從初始位置旋轉至接收器位置時的旋轉角度，通過同步脈沖激光器發出的時間信息差tj和發射站的旋轉周期T表示

(3)

假設把小范圍的測量區域定義為整體坐標系，則對于任意的發射站i在發射站坐標系向整體坐標系的旋轉矩陣為Ri，平移矩陣為Ti，則在整體坐標系下，當激光平面掃過接收器時的光平面系數可以表示為

(4)

此時對于任意發射站i，當兩個光平面掃過接收器Pm(xm,ym,zm)時，在整體坐標系下的光平面方程可以表示為

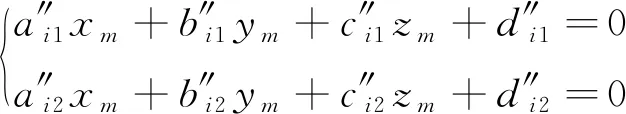
(5)

在工作空間測量定位系統外參(Ri,Ti)標定完成后，當測量區域內的發射站數量i≥2時，即可利用最小二乘法對式(5)進行求解，進而得到待測接收器處的三維坐標[17-18]。

2 試驗描述

試驗設備主要用到wMPS與逆向工程試驗臺,如圖3所示。圖3中:wMPS選用4臺最新樣機(采樣頻率20 Hz)和一個接收器。如圖4所示，逆向試驗臺采用曲柄連桿原理搭建，根據曲柄連桿原理可知滑塊位移s不是做簡諧振動，但是方程高次項的取舍與λ的取值有很大的影響，在航空發動機中，λ的取值范圍在0.26～0.31，通過二項式定理展開的高于λ4項可以被舍去[19]，根據這一規則，如果本次試驗設計λ<1/10，則可以直接把高于λ2項都舍去，位移方程近似為s=R(1-cosα)。則通過計算機控制伺服馬達按規定轉速旋轉使傳動軸拉動滑塊在直線導軌上做近似簡諧振動，其中傳動輪盤半徑R即是簡諧振動振幅。

圖3 試驗臺現場圖

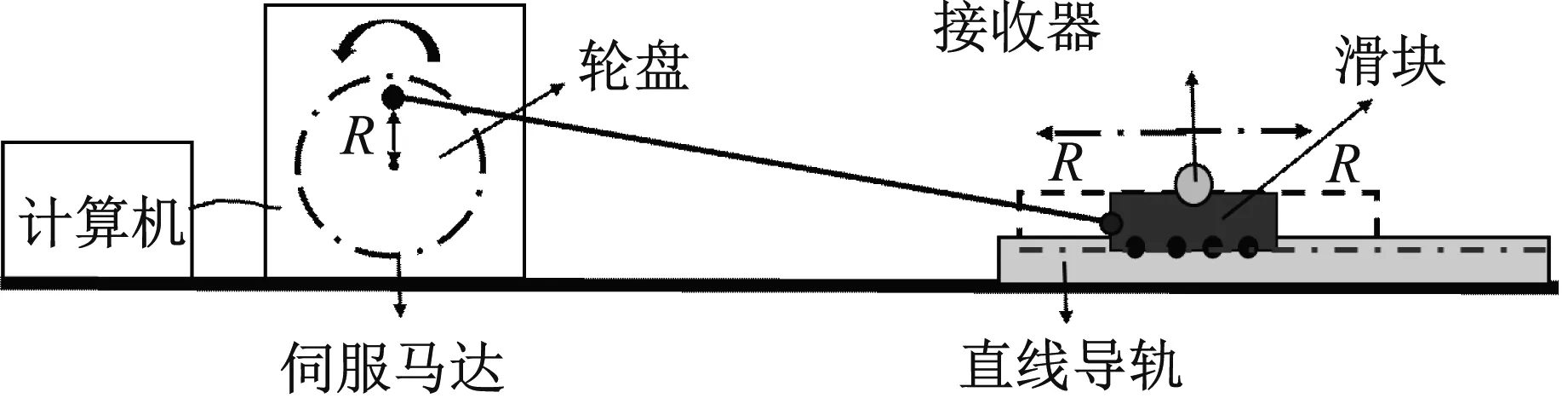
圖4 試驗臺簡化圖

輪盤的半徑R分別為3 mm,5 mm,10 mm,20 mm,30 mm。為確保每一測段試驗中振動臺沒有發生位移，把試驗設備安放在大理石地面上，在試驗臺前約3.5 m位置用4臺發射站進行組網定向，并確保接收器能收到每一臺發射站的信號，試驗數據采集時間為2 min，按振動頻率為0.5 Hz,1.0 Hz,2.0 Hz,3.0 Hz,4.0 Hz(4.0 Hz已滿足測量大多數結構的固有參數)依次測量每段數據。

3 數據預處理

由于wMPS不能進行對中整平，雖然可以用其他儀器布設控制點進行標定，但考慮到試驗臺整平也會引入誤差，因此采用最小二乘擬合的方法建立獨立坐標系統。把每一測段所測數據擬合成一條直線(近似滑塊運動軌跡)作為直線運動的基準線(即X軸)，垂直于試驗臺的方向定義為Z軸，根據右手螺旋定則定義Y軸，建立空間直角坐標系。3 mm-1 Hz測段轉換到新坐標系后的X,Y,Z坐標軸數據，如圖5所示。從圖5可知:X坐標軸數據是滑塊的真實運動位移，Y,Z坐標軸數據振蕩非常小，被認為是測量帶來的噪聲[20]。

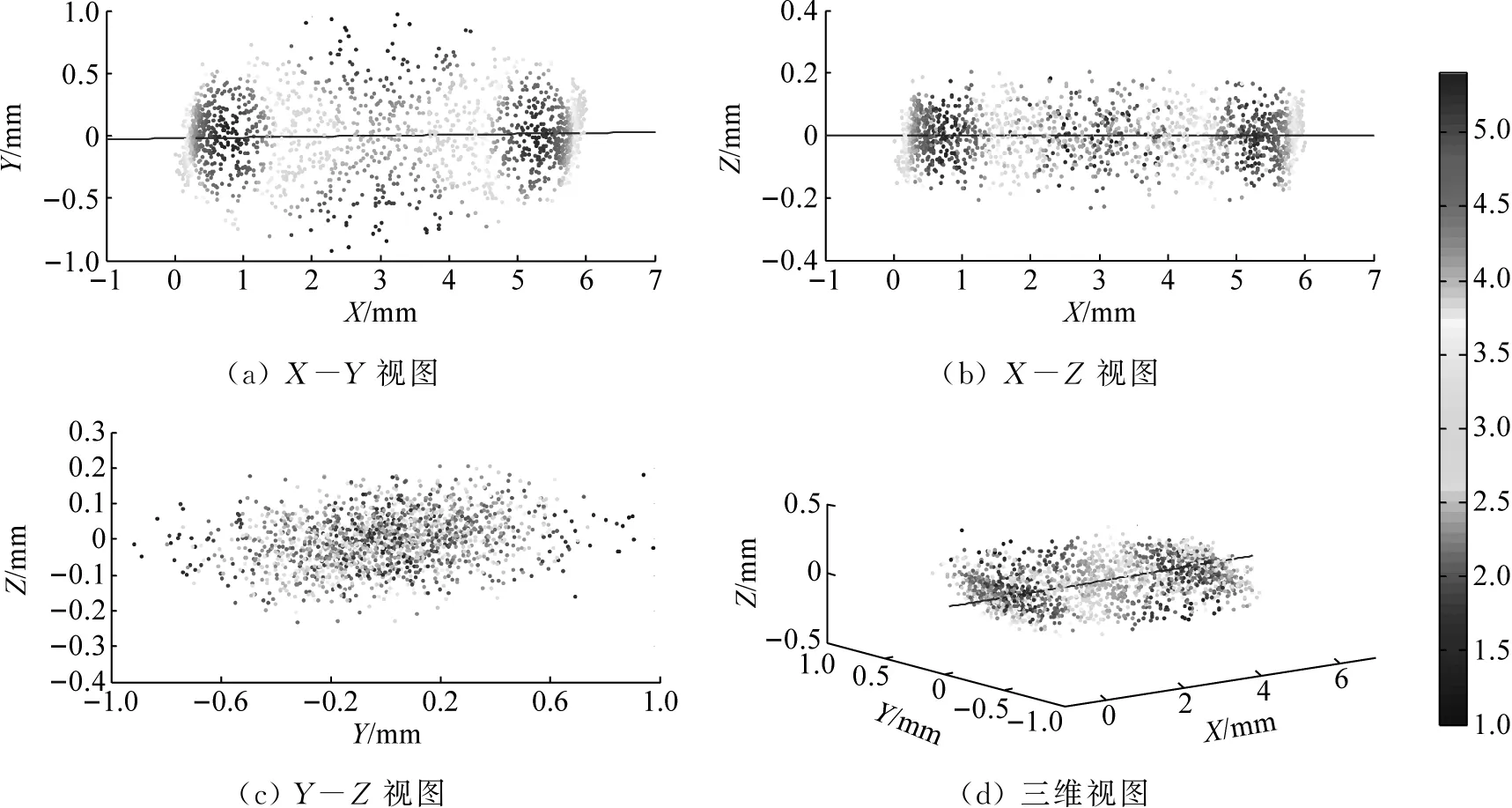
圖5 3 mm-1 Hz測段坐標轉換后數據

4 時間序列分析

4.1 粗差剔除

本文采用伺服馬達控制輪盤旋轉做簡諧振動方法與Psimoulis等[21]用彈簧做介質做簡諧振動方法不同，本試驗能保證數據的連續性，在試驗中引入的誤差更少，在保證能測定wMPS性能的同時也使試驗更加簡單，且對測定wMPS的性能沒有影響。在各測段數據中，只有測量頻率較大測段有極少數測點跳動明顯，這是由于受到多種偶然因素而引入的粗大誤差[22]，如現場突然震動或偶然反光等的影響。常用粗大誤差剔除方法有目測法、均方根法、中值濾波法等，本文采用目測法剔除并進行插值，對結果分析不會產生影響。沿著Y軸測量的時間序列光譜分析，結果如圖6所示。由于其表現為測量白噪聲，因此不再深入研究。

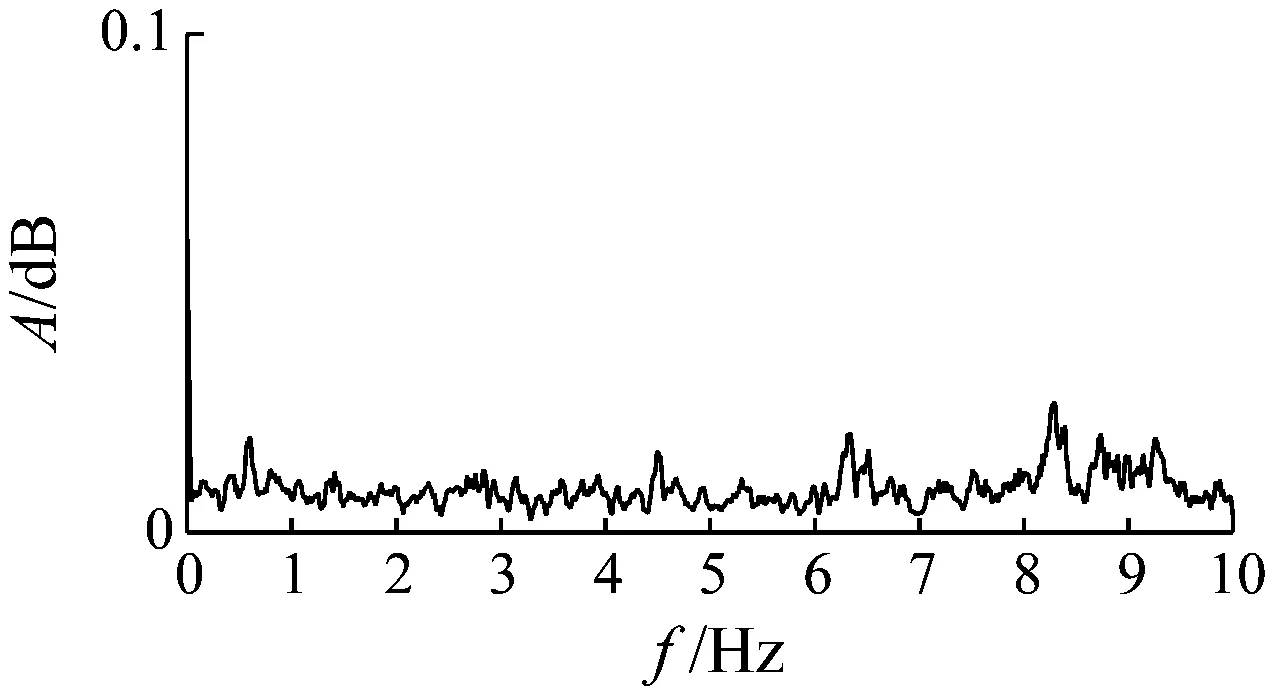
(a) 1.0 Hz

4.2 振幅誤差分析

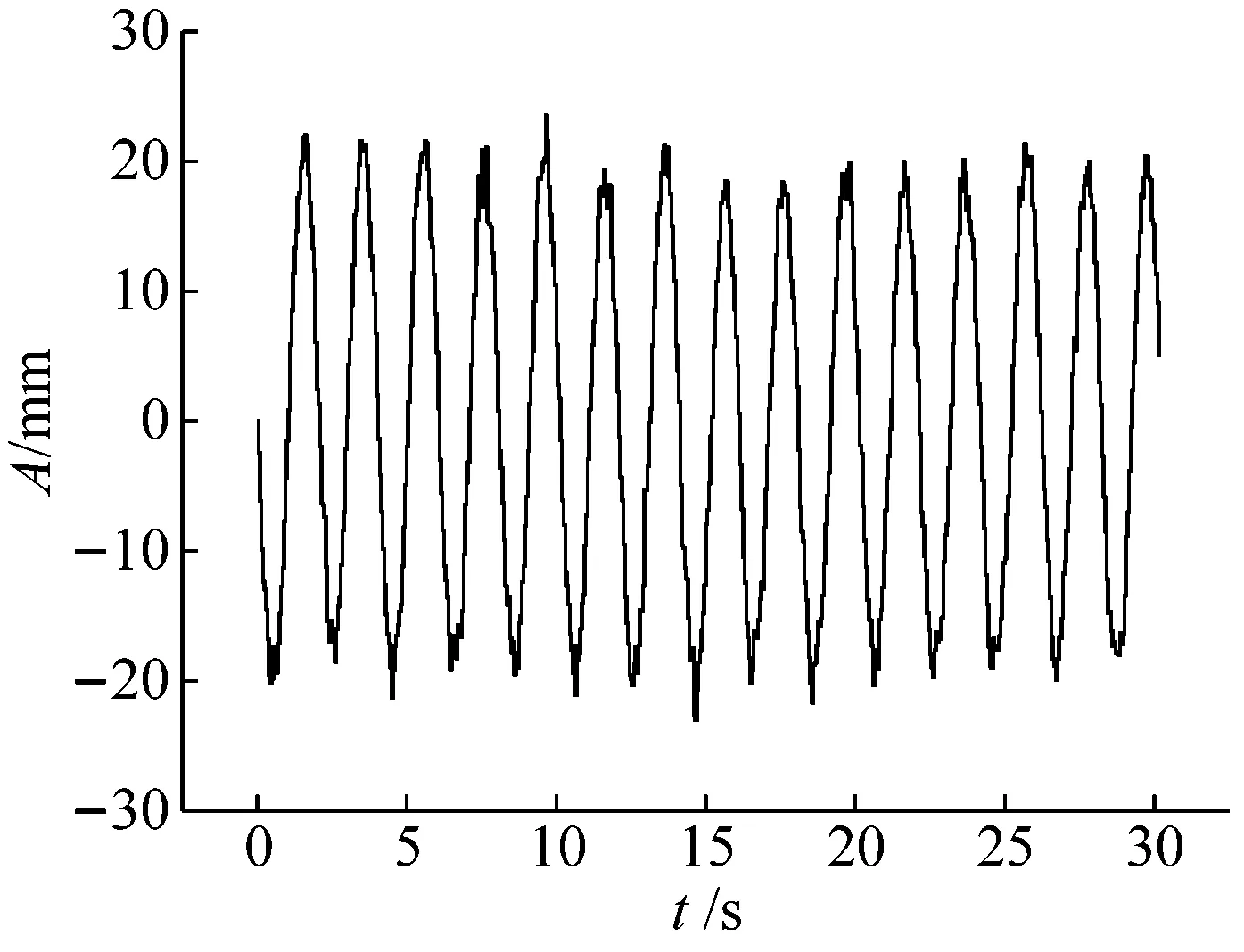
主要通過實測振幅與真實振幅做比較來評定測量的準確性，真實的振幅是每一個輪盤的半徑(設計值)。通過提取實測波峰和波谷的值與真實的振幅做比較，10 mm振幅0.5～4.0 Hz各測段振動位移，如圖7所示。所測段振幅絕對偏差與中誤差，如表1所示。可以看出：偏差值在(0.05±0.06) mm～(3.28±4.40) mm，誤差規律是隨著振幅和頻率的增大而增加，與Psimoulis等研究的評定RTS誤差規律相似，但絕對偏差值比RTS評定的值小很多。圖8更直觀的展示其誤差分布情況，可以直觀的看出當振幅在3 mm時，在4.0 Hz振動的振幅絕對偏差依然在亞毫米以內。

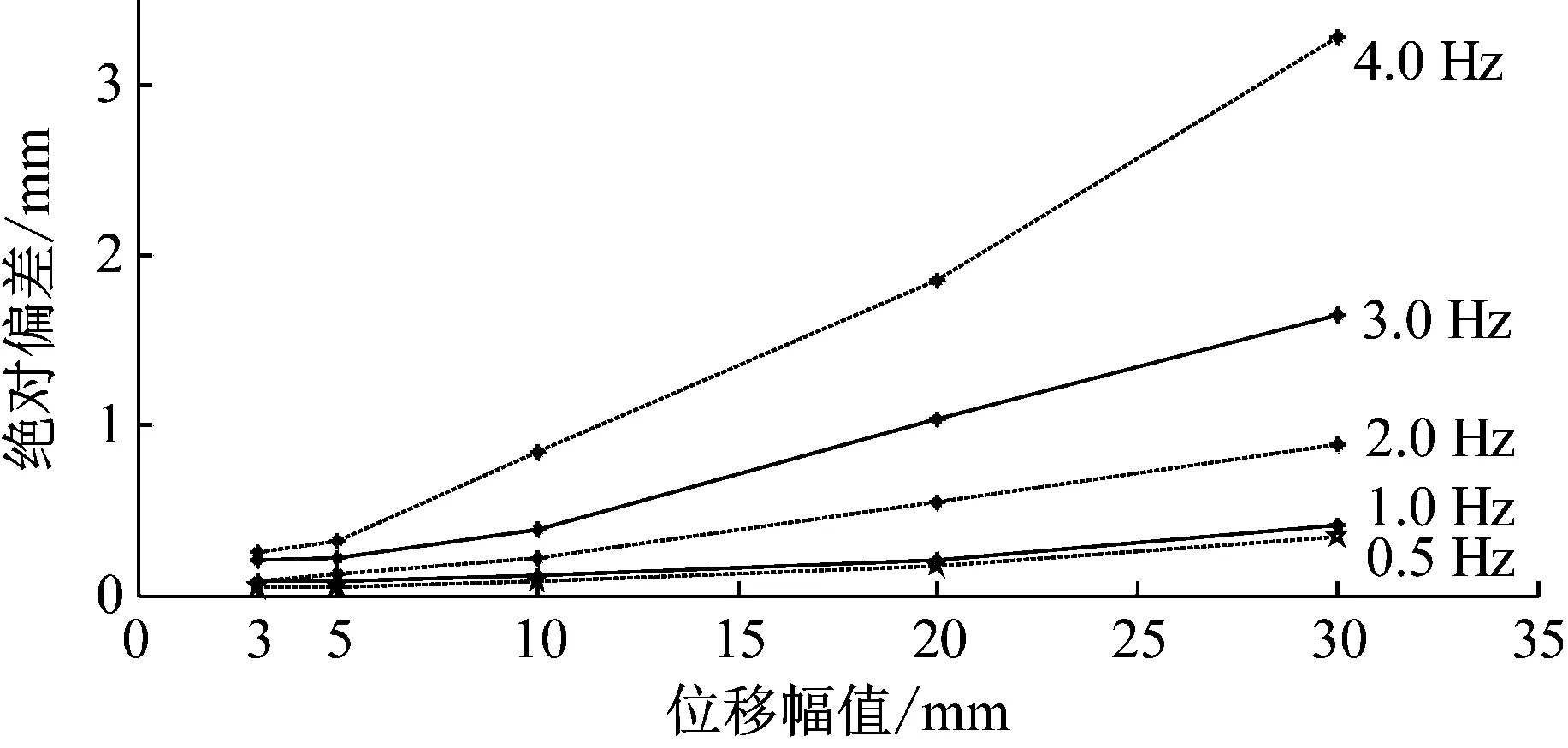
圖8 不同測段振幅絕對偏差直觀圖

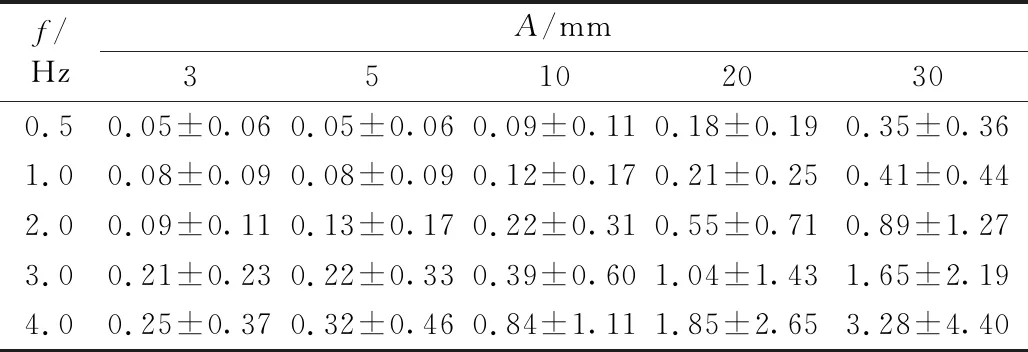
表1 不同測段振幅絕對偏差

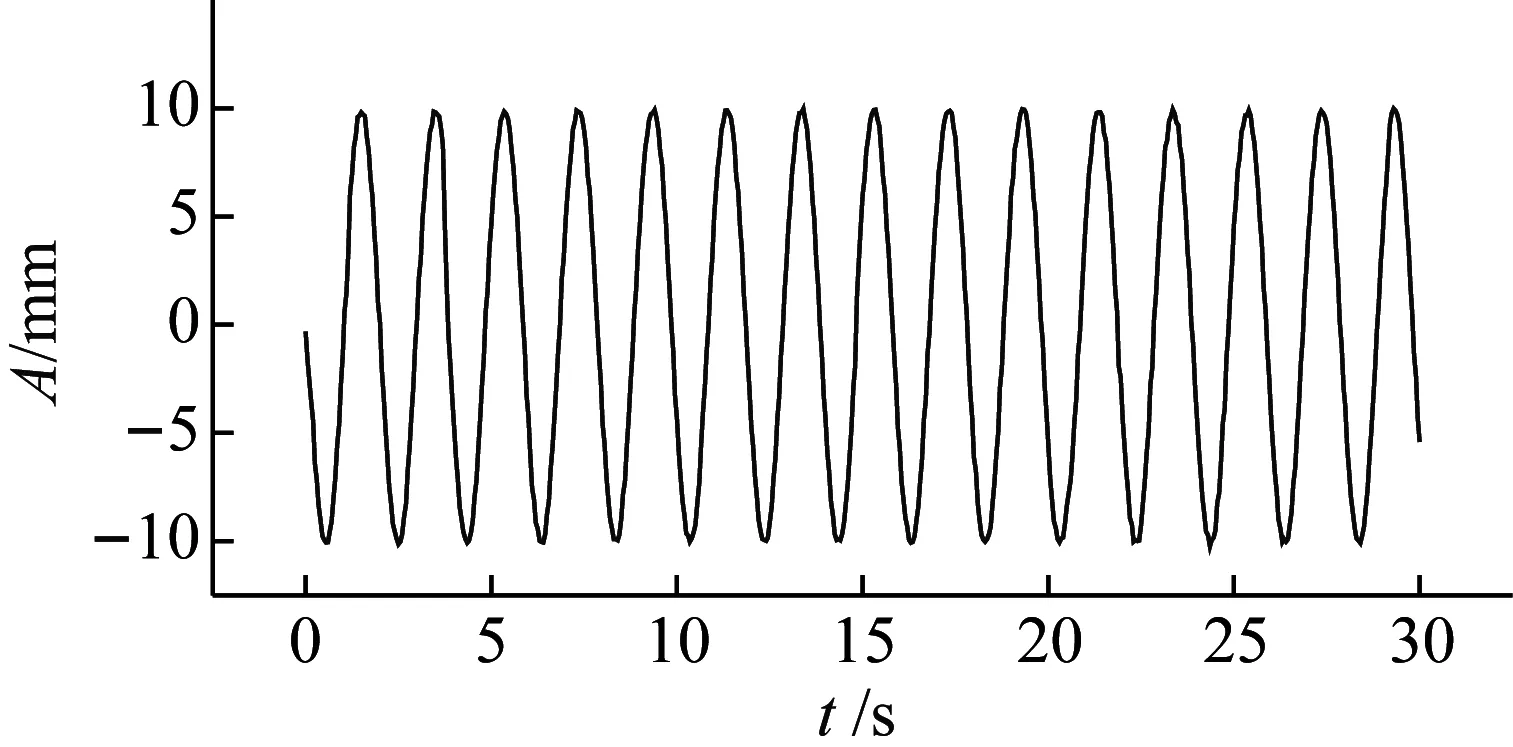
(a) 0.5 Hz

4.3 固有頻率提取

利用FFT方法提取各測段數據頻率，所有測段的計算結果，如表2所示。10 mm振幅從0.5～4.0 Hz各測段獲取的時間序列分析結果,如圖9所示。圖9中小峰值振幅的增大反映了觀測中信噪比的降低。從表2可知：從0.5～4.0 Hz各測段都可以準確獲取主頻率值，最大偏差小于4.0%，3 mm,5 mm位移的計算結果基本相同，當振幅為30 mm時，依然可以測出4.0 Hz的頻率，從此得出，wMPS可以在振幅為3～10 mm時獲取到4.0 Hz頻率，滿足測量剛性結構的固有參數的要求。

(a) 0.5 Hz

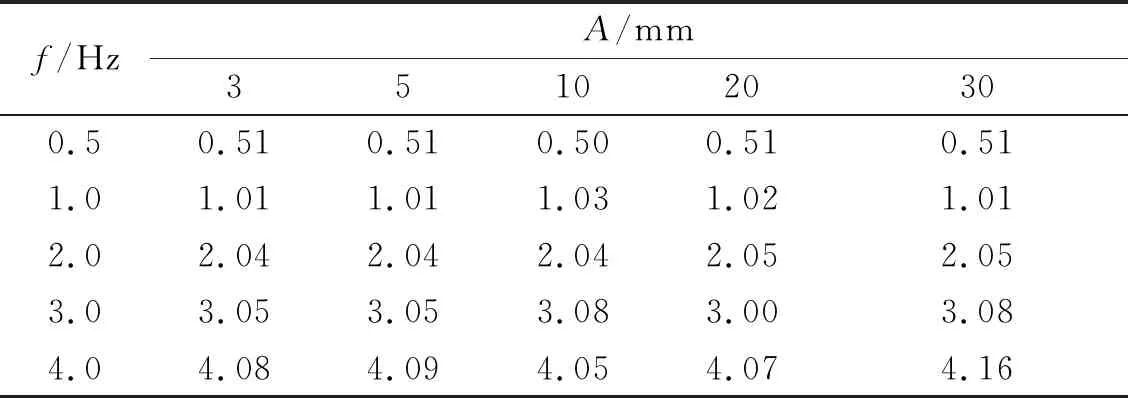
表2 各測段實測振動頻率值

5 對比試驗與分析

為進一步分析wMPS測量剛性結構固有參數的可行性，如圖10所示，采用三星座(全球定位系統、格洛納斯、北斗衛星導航系統)組合GNSS-RTK(global navigation satellite system-real-time kinematic)(水平精度8 mm+1 ppm，垂直精度15 mm+1 ppm)在天津大學校內寬闊場地進行對比試驗。由于條件的限制，基準站采用Trimble R12，移動站采用Trimble R10，移動站采樣頻率設置為20 Hz，基準站與移動站距離29.5 m，衛星截止高度角設置為10°，整個試驗過程中接收衛星數不少于14顆。

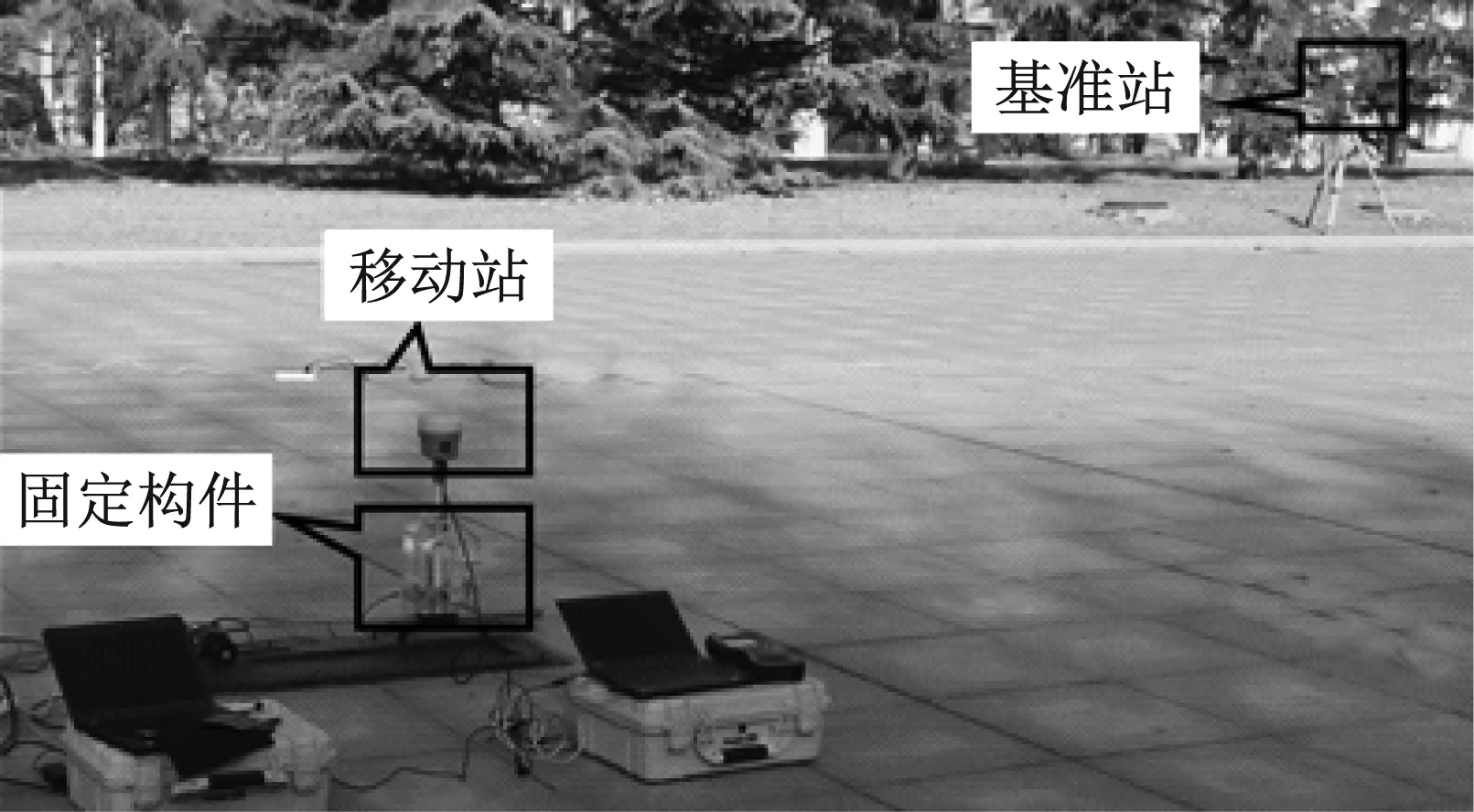
圖10 試驗現場圖

由于GNSS-RTK豎直方向精度遠低于水平方向精度，因此只對水平方向進行測試。通過調節底座板使導軌處于水平狀態，并進行數據采集。圖11為1 Hz時3 mm,5 mm和10 mm振幅點云圖。從圖11可知：當振幅為3 mm和5 mm時很難識別出滑塊運動位移，主要是由于振動幅值小于儀器水平精度，當振幅為10 mm時，可以明顯識別出滑塊運動軌跡，采用第3章數據處理中的方法定義坐標系，把每一測段所測X，Y數據擬合成一條直線作為運動的基準線，計算振幅為10 mm，20 mm和30 mm測段的絕對偏差與中誤差，結果如表3所示。20 mm振幅各測段實測振動位移，如圖12所示。

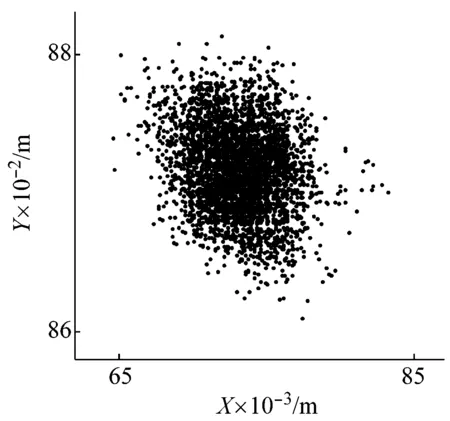
(a) 3 mm振幅X-Y視圖

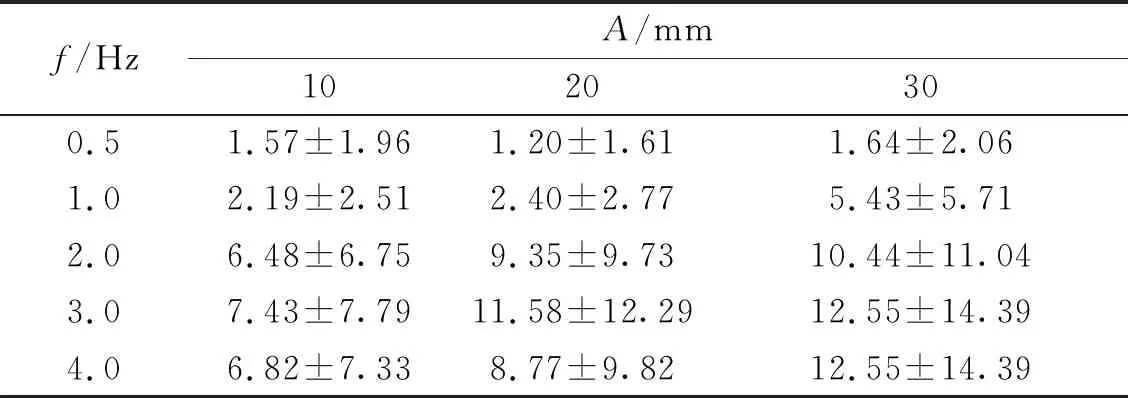
表3 GNSS-RTK不同測段振幅絕對偏差

(a) 0.5 Hz

利用FFT方法提取各測段數據頻率，所測段的計算結果，如表4所示。3 mm振幅從0.5～4.0 Hz各測段獲取的時間序列分析結果，如圖13所示。

從表4和圖13可知：GNSS-RTK可以識別出振幅3～30 mm、0.5～4.0 Hz的主頻率。但是從表3與表1的對比，圖11和圖12與圖7的對比中可知：GNSS-RTK測量剛性結構振動位移的準確性要遠低于wMPS，首先3 mm與5 mm振幅的位移很難直接識別，其次得到振幅的絕對偏差與中誤差遠大于wMPS，這種結果主要是受到GNSS-RTK測量精度的限制。同時，也體現出wMPS在測量剛性結構固有參數時的優勢。

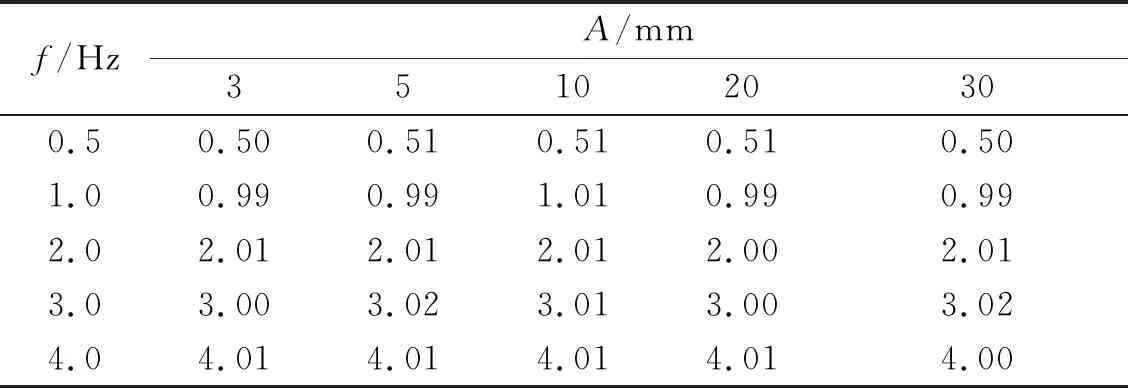
表4 GNSS-RTK各測段實測振動頻率值

(a) 0.5 Hz

6 結 論

從分析結果可知：wMPS在測量剛性結構固有參數有明顯的優勢。首先，wMPS測量數據精度高，發射站轉速快，采樣頻率高；其次，可同時對多個目標點直接測量，并通過增加發射站，可擴大量程。同時也表明，wMPS完全可以滿足測量剛性結構固有參數的工作，在振幅3 mm時可以準確獲取4.0 Hz頻率值，在30 mm大振幅時依然可以獲取4.0 Hz頻率值。

由于wMPS單站測量距離最大25 m，限制了其測量大型結構固有頻率的可行性，但是測程更大轉速更快的發射站已經在試驗中，未來wMPS在測量結構固有參數的應用前景廣闊，對結構健康監測的發展有重要的參考意義。