動力吸振器在聲黑洞單元中的放置位置對減振效果的影響

賈秀嫻， 趙 劍， 杜 宇， 于 野

(大連理工大學 汽車工程學院,遼寧 大連 116024)

隨著近些年來能源問題和環境問題的日益嚴重，為了降低運載工具的傳統能源消耗以及減少污染排放，輕量化研究成為運載工具發展的必然趨勢。然而，減輕結構質量，在一定程度上會惡化振動及噪聲性能。因此，如何在輕量化的同時保持甚至提高減振降噪性能已成為汽車、高速列車、船舶以及航空航天運載工具的研究熱點之一。一種基于聲黑洞(acoustic black hole,ABH)理論的結構，其可以潛在地實現使用較少附加質量就可有效控制結構振動噪聲響應，因此逐漸得到越來越多的關注和研究。

Pekeris[1]觀察到，在分層、非均勻的媒質中，橫截面的厚度線性衰減到0之后，聲波并沒有發生反射。Mironov[2]研究波在楔形體中傳播時指出，當楔形體的截面輪廓變化符合一定指數規律時，即h(x)=εxm(其中ε為常數，m為正有理數，且m>2)，且當其厚度平滑地減小為0時，其內彎曲波傳播到厚度為0的點(奇點)時，相速度趨于0，即波無法到達楔形板的末端，從而不會發生反射。基于這一效應，Krylov等[3-8]提出ABH的概念，并利用ABH效應對結構進行了一系列的減振研究。理論上，ABH結構可以吸收100%的入射波能量，并可應用于空氣環境或者液體環境中的不同工程結構，同樣也適用于使用Lamb波的超聲波設備。然而任何實際結構都不可能存在0厚度，加工過程中的制造偏差、切割工具引起的卷曲以及過早的切斷，使得實際存在的ABH結構邊緣均具有一個具體的厚度，其反射能量可達50%～70%。研究表明，即使邊緣厚度的存在、制造工藝不足夠精準等缺陷會削弱ABH的聚焦效應，但ABH結構也能夠被廣泛地應用，起到減振降噪的有效作用。實際應用中的ABH結構截面輪廓變化規律為h(x)=εxm+hmin，其中hmin為ABH區域的最薄厚度，輪廓變化如圖1所示。圖1中h0為均勻厚度區域的厚度。

圖1 聲黑洞結構示意圖

以周期性排列著ABH單元的變厚度板結構為主要研究對象，Conlon等[9-11]從聲功率、損耗系數、模態損失因子、能量流在變厚度板結構中的分布、ABH單元的動態特性及參數設計等方面進行了研究，討論了該結構的振動衰減效果。結果表明：周期性排列的ABH結構可以使輻射聲功率減少高達20 dB。而且使用多個動力吸振器(dynamic vibration absorber，DVA)針對一個激勵頻率下的振動進行減振控制相對于單個DVA效果要好很多[12]。當分布式的動力吸振器應用在ABH單元周期性排列的變厚度板結構時，被證明在寬頻帶內有較好的減振效果。但是，由文獻[13]可知，在某些頻率下，將DVA放置在ABH結構的中心位置時減振效果并不明顯。其原因可能是在實際模型中，ABH中心位置的厚度大于0，與基于等于0的理論假設不符，從而導致聚焦位置并不在ABH的中心。因此，將DVA放置在該位置的減振效果不符合理論預期。此外，在某些模態下，ABH的中央位置還有可能成為動態響應為零的點，這時將DVA放置在該位置時勢必不會產生任何減振效果。因此，DVA放置位置對減振效果的影響至關重要，而根本原因是聚焦位置。

本文首先通過射線聲學理論直觀展示了不同入射角度下ABH結構的彎曲波聚焦路徑，初步了解彎曲波在ABH結構中的傳播路徑和聚焦位置。其次，使用數值搜索法[14]確定多個DVA的參數。最后，通過有限元仿真計算對比分析兩種DVA布置方案(即ABH單元中心位置和聚焦位置)的振動響應。

1 ABH結構的彎曲波聚焦位置

在ABH理論中，假設其中心位置厚度為0，其聚焦位置必然位于中心處。但實際物體中的ABH無法加工成0厚度(即hmin≠0)。因此，其聚焦位置可能不在中心處。通過使用射線聲學理論，可以直接觀察到嵌入ABH結構變厚度板中彎曲波的傳播路徑以及聚焦位置。本文分別探究了兩種入射方式下的彎曲波聚焦位置，即中央點源激勵和平面波激勵。

1.1 數值模型參數

使用的ABH結構為半徑R=100 mm的圓形，即x0=100 mm，如圖2所示。由圖1中的冪律輪廓以最薄點為中心旋轉形成，4個同尺寸的ABH結構對稱地嵌入在一塊無限大的自由邊界板中，相鄰兩個ABH結構的中心間距為d=204 mm。板的均勻厚度部分h0=8 mm，ABH區域最薄處(即圓心處)厚度為hmin=1 mm，厚度變化的冪指數設為m=2.2。板結構材料為鋼，彈性模量E=196 GPa，密度ρ=7 850 kg/m3，泊松比v=0.3，假設無材料阻尼。從圖2可知，板左側箭頭為平面波激勵方向，位于板幾何中心處三角形內的點代表點源激勵位置。

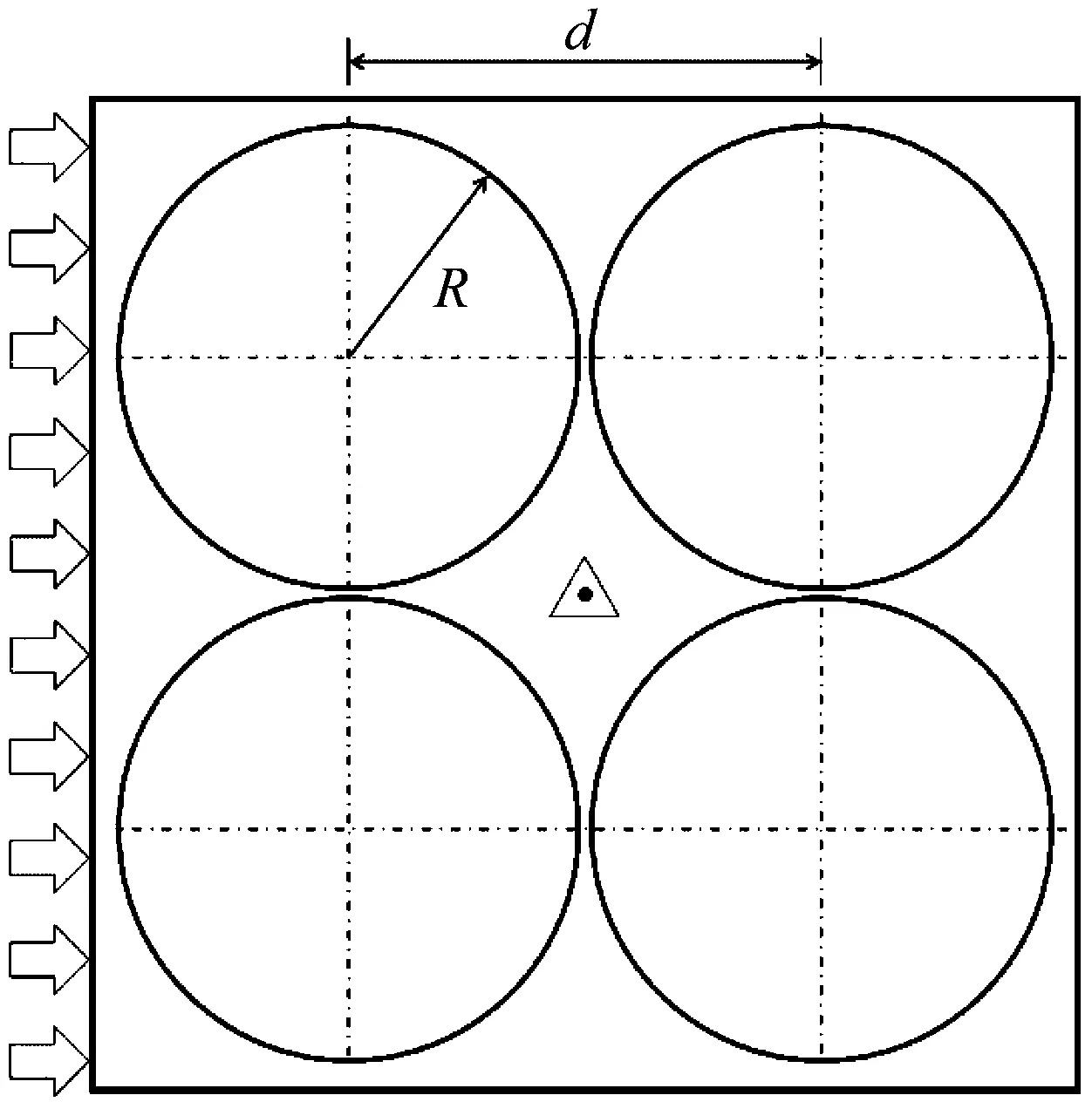
圖2 結構模型的示意圖

1.2 射線聲學

射線聲學，即幾何聲學，類似于幾何光學方法，聲音以射線形式傳播。在射線聲學的范疇內，有兩個基本的方程：一個是用于確定聲線行走軌跡的程函方程；一個是用于確定單根聲線強度的強度方程。這兩個方程可以在一定的近似條件下得到。非耦合彈性波射線的運動軌跡方程[15]為

(1)

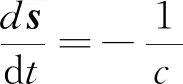
(2)

1.3 中央位置的點源激勵

在不考慮反射波的情況下，使用MATLAB軟件對式(1)和式(2)求解，得到彎曲波在ABH結構中的傳播軌跡。變厚度板結構在30 kHz頻率的中央點源激勵下彎曲波傳播的軌跡圖，如圖3所示。入射角從原點出發(見圖2)，每隔6°增加一條入射線模擬點源激勵。以板的幾何中心(0，0)為原點，4個象限內相應于原點處點激勵的響應關于幾何中心對稱，故取第一象限討論。第一象限中ABH單元的幾何中心坐標為(102 mm，102 mm)，圖3中彎曲波在第一象限的聚焦位置為(125.98 mm，125.95 mm)，二者并不重合。

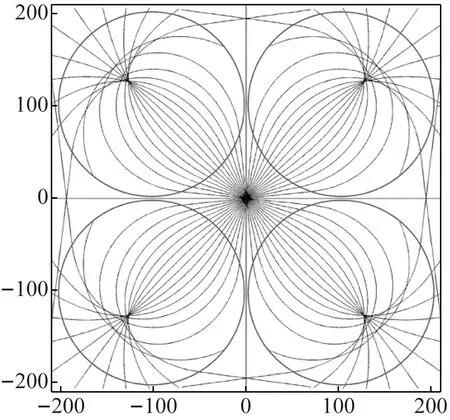
圖3 30 kHz點激勵條件下彎曲波的傳播軌跡(mm)

1.4 邊界位置的平面波激勵

當平面波激勵從板的一側進入(見圖2左端入射)，模型設入射角為0°，每隔5 mm增加一條入射線，共80條平行入射線。變厚度板結構在30 kHz平面波激勵下彎曲波傳播的軌跡圖，如圖4所示。以板中心為原點，圖4顯示在第一、第二象限的聚焦位置分別為(132 mm, 102 mm)和(-72 mm, 102 mm)。若以每個ABH單元的中心為原點分別建立坐標系，則彎曲波在這兩個單元中相對于各自圓心的聚焦位置相同。此結論也同樣適用于第三、第四象限。

圖4 平面波激勵條件下彎曲波傳播軌跡(mm)

與點源激勵仿真結果類似，當ABH結構的最薄處厚度不為0時，其對彎曲波產生的聚焦位置與ABH結構幾何中心不重合。

2 DVA的位置對減振效果的影響

2.1 結構模型

使用4個DVA對結構進行減振，每個ABH單元內布置一個DVA。由文獻[13]以及第1章的研究結果可知，為了提高減振效果，當附加DVA時，ABH結構的中央位置(即厚度最薄處)并非最佳位置。本節利用有限元仿真的方法得到中央點源激勵在3 677 Hz下ABH單元的聚焦位置，其在第一象限中的坐標為(130 mm, 130 mm)，而第一象限中ABH單元的幾何中心位置為(102 mm,102 mm)。未加DVA的變厚度板(variable thickness plate,VTP)模型。根據放置位置的不同將附加DVA的模型分為兩種:一種是將DVA放置在ABH單元的中心位置(VTP-DVA-Center)，以板中心為零點，整體結構為中心對稱結構，DVA在第一象限的坐標為(102 mm, 102 mm);另外一種是放置在能量聚焦處(VTP-DVA-Focus)，DVA在第一象限的放置位置坐標為(130 mm, 130 mm)。

2.2 參數優化

DVA參數的優化目標是針對3 677 Hz激勵條件下產生的共振峰進行優化，同時使得3 677 Hz附近一定帶寬內(4個DVA中最小共振頻率2 985 Hz，最大共振頻率4 042 Hz)的響應得到較好的控制。假設板結構為無阻尼結構，DVA的剛度ki(i=1,2,…,6)保持一致，第i個DVA的固有頻率、質量、阻尼分別為

(3)

(4)

ci=2miξTωi

(5)

通過使用數值搜索技術，獲得DVA的最優參數公式

(6)

(7)

(8)

DVA的總質量與板結構的質量比μ=0.1，當DVA的個數n=4時，計算得到調諧頻帶寬β=0.3，調諧頻率比f=0.96，阻尼比率ξT=0.082。各個DVA的參數，如表1所示。

表1 DVA參數

2.3 加速度頻率響應云圖

通過使用Hypermesh有限元軟件進行前后處理，板結構使用四面體單元進行網格細致劃分，采用Nastran有限元分析軟件進行求解計算(該有限元仿真方法的可靠性和精度已經在之前的研究工作中得到詳細論證)。通過計算得到了垂直于板面方向的加速度頻響云圖，如圖5所示。圖5(a)為未加DVA時的加速度響應，圖5(b)為將DVA附加在ABH結構中央位置的加速度響應，圖5(c)為DVA放置在能量聚集位置處的加速度響應。模型VTP，VTP-DVA-Center,VTP-DVA-Focus在云圖中的最大值分別為：2.34×107mm/s2，3.26×104mm/s2，8.63×103mm/s2。分析可知，加了DVA之后，最大值至少降低了57 dB。而且，將DVA放置在能量聚集位置比放置在ABH單元的中心位置衰減了11.5 dB。通過觀察云圖的色度區域可知，加了DVA之后，較大響應區域的面積是減小的，而且，VTP-DVA-Focus的較大值區域面積較前兩種情況顯著減少。

圖5 3 677 Hz激勵頻率下的加速度響應云圖

2.4 平均加速度頻率響應對比

2.3節中板上所有節點的平均加速度在2 700～4 200 Hz頻帶內的頻率響應曲線，如圖6所示。第f個激勵頻率下的平均加速度響應值Af為

(9)

式中:f=1,2,…,m，m為激勵頻率的總個數;ai為第i個節點的加速度值，i=1,2,…,n;n為仿真模型中的總節點個數。

表2所示有3條曲線的各峰值。加了DVA之后，加速度平均響應的峰值得到較大幅度的抑制，第一個峰值降低了至少26.9 dB，第二個峰值降低了至少27.9 dB,如圖6所示。而且，當將DVA放置在能量聚集位置處時，峰值減少為一個，另外，相對于VTP-DVA1模型在約3.8 kHz的峰值衰減了16.7 dB。

圖6 板的平均加速度響應

表2 各板的總平均加速度值及平均加速度響應曲線的峰值

在2 700～4 200 Hz內，板的總平均加速度響應值Aw為

(10)

各板的總平均加速度值(見表2)。在頻帶內附加DVA后，加速度總平均響應明顯降低。并且相比將DVA布置在ABH中心，放置在聚焦位置的總平均加速度值降低幅度更大。

3 結 論

本文以周期性排列的ABH結構為研究對象，使用多個DVA對一個頻率進行振動控制。通過調整DVA的放置位置，使結構的振動衰減效果達到更高的水平。通過有限元仿真得到板結構的加速度響應的云圖以及平均加速度響應曲線，探討了DVA的放置位置對減振效果的影響。結論如下：

(1) 應用射線聲學理論方法獲得彎曲波傳播的軌跡，觀察到當ABH結構的最薄厚度不為0時，其聚焦位置沒有出現在其幾何中心位置。

(2) 對于3 677 Hz的共振頻率，放置在能量聚焦處的DVA結構能夠更有效地衰減板的平均加速度響應峰值，與放置在ABH單元中心位置相比，其最大峰值衰減了16.7 dB，同時峰值的數量由3個減少為一個。

(3) 通過對比總體平均加速度，可知附加DVA在2 700～4 200 Hz內具有明顯的振動衰減效果，尤其是當把DVA放置在ABH聚焦位置時，總平均加速度值降低了28 dB。比DVA在中心位置時衰減了9.2 dB，明顯優于放置在ABH中心處。