RC橋墩殘余位移指標影響因素分析及貝葉斯估計

曾武華， 卓衛東， 王東升

(1. 三明學院 建筑工程學院， 福建 三明 365004； 2. 福州大學 土木工程學院， 福州 350108；3. 河北工業大學 土木與交通學院， 天津 300401)

傳統的橋梁抗震設計方法通過提供結構足夠的強度和延性，防止其在大震作用下發生倒塌破壞[1]。然而，由于抗側力的關鍵構件(如橋墩等)在大震中受損嚴重或整體殘余位移過大等原因，橋梁往往在震后需要拆除重建。1995年日本阪神地震震害調查發現，若鋼筋混凝土(reinforced concrete，RC)橋墩的殘余位移比(即墩頂殘余位移與墩高之比)超過1.75%，橋梁就需要拆除重建[2]。由此可見，鋼筋混凝土橋墩的殘余位移比可作為橋梁結構抗震韌性設計的重要參數之一。目前，橋墩殘余位移驗算已被寫入一些國家的橋梁抗震設計規范，被認為是橋梁結構可修復性的重要描述指標[3-5]，但我國現行橋梁抗震設計規范[6]尚缺乏關于殘余位移的相關規定。

已有研究認為，強震后鋼筋混凝土橋墩的可修復性可通過定義無量綱化的殘余位移指標來量化評價。Hose等[7]在對大量鋼筋混凝土墩柱擬靜力試驗結果分析的基礎上，定義了一個以屈服位移為歸一化參數的無量綱化的殘余位移指標——殘余位移延性指標。羅征等[8]基于5根鋼筋混凝土空心墩柱的擬靜力試驗結果，探討剪跨比和配箍率對殘余位移延性指標的影響，發現剪跨比與配箍率兩參數的變化對殘余位移延性指標無影響。王軍文等[9-10]采用數值模型，計算分析了軸壓比、長細比、縱筋配筋率、體積配箍率、縱筋強度硬化系數、縱筋與混凝土強度比等參數對橋墩殘余位移延性指標的影響；結果表明，鋼筋混凝土橋墩殘余位移延性指標隨軸壓比、縱筋強度硬化系數、體積配箍率、長細比的增大而減小。此外，還有一些研究分別提出了以墩高、最大位移等作為歸一化參數的無量綱化的殘余位移指標定義。李宇等[11]采用橋墩殘余位移比，定量化描述了橋梁結構5個不同水平的損傷性能目標。蔡曉玉等[12]以一座連續梁橋為研究對象，采用增量動力分析方法，得到了基于橋墩殘余位移比的結構倒塌判定指標。曾武華等[13]基于鋼筋混凝土橋墩的擬靜力試驗結果，給出極限狀態下橋墩殘余位移比的統計結果。胡曉斌等[14]研究了強震作用下單自由度體系殘余位移的離散性問題，結果表明，殘余位移及殘余位移延性指標的離散性最大，而殘余位移與最大位移之比的離散性最小。

由于影響鋼筋混凝土橋墩殘余位移指標的因素較多，目前學者們對殘余位移指標的影響因素及其影響程度仍未達成共識；此外，已有試驗和分析數據等均具有一定的不確定性，目前發現其殘余位移的統計離散性較大。鑒于此，本文結合擬靜力試驗和數值模擬分析，研究鋼筋混凝土橋墩的基本設計參數對其殘余位移指標的影響規律，并采用回歸分析方法得到其殘余位移指標的經驗計算公式；在此基礎上，基于貝葉斯更新理論對殘余位移指標進行估計，建立鋼筋混凝土橋墩殘余位移指標的概率模型。

1 殘余位移指標影響因素分析

1.1 有限元計算模型

為了驗證數值模型的可靠性，利用OpenSees軟件，首先建立Lehman等[15]試驗采用的鋼筋混凝土墩柱試件的有限元計算模型；其中，墩柱試件采用基于力的非線性梁柱單元模擬；混凝土本構關系采用concrete04模型，約束混凝土的本構采用的是Mander提出的約束混凝土應力-應變關系，鋼筋本構關系采用reinforcingsteel模型[16-18]。對計算模型施加試驗反復荷載，模擬Lehman等開展的擬靜力試驗。

圖1和圖2分別給出了Lehman等試驗中兩個典型試件(415試件和430試件)的試驗滯回曲線與數值滯回曲線的對比情況；從圖1中可見，兩者吻合較好。

圖1 415試件試驗結果與數值計算結果比較

圖2 430試件試驗結果與數值計算結果比較

1.2 參數分析

已有研究表明，鋼筋混凝土橋墩的軸壓比、剪跨比、配筋率和配箍率是影響其震后殘余位移的主要因素。由于受到經費、時間等條件限制，已有試驗無法全面考慮這些因素對鋼筋混凝土橋墩殘余位移的影響，故本文以軸壓比、剪跨比、配筋率和配箍率作為基本參數，每個參數取4個水平(如表1所列)，采用全面試驗設計方法，通過改變Lehman等試驗試件的相應參數，建立了256個圓形橋墩試件樣本。

利用OpenSees軟件，采用1.1節經驗證的建模方法，建立所有橋墩樣本的有限元計算模型，進行擬靜力加載。通過有限元計算分析，得到了256個圓形橋墩試件的荷載-位移滯回曲線，以及橋墩試件在變形極限狀態下的殘余位移及最大位移值。本文將以下3個條件： ① 縱向鋼筋屈曲；② 水平箍筋斷裂；③ 橋墩水平承載力下降到最大承載力的85%；之一發生即定義為橋墩變形極限狀態達到的標志。為了確定橋墩殘余位移能力，僅考慮橋墩達到變形極限狀態時，其卸載后的墩頂殘余位移。

本文分別以墩高和最大位移作為歸一化參數，定義兩個無量綱化的殘余位移指標，即殘余位移比δrh和殘余位移與最大位移比δrm，分別如式(1)和式(2)所示

δrh=Δr/H

(1)

δrm=Δr/Δm

(2)

式中：Δr為當橋墩達到變形極限狀態時，其卸載后墩頂殘余位移；H為墩高；Δm為當橋墩達到變形極限狀態時，墩頂最大位移。

根據式(1)和式(2)的定義，采用統計分析方法，得到了256個橋墩試件的殘余位移指標δrh和δrm的統計特征值，如表2所示。由表2可見，殘余位移比δrh的變異系數大于殘余位移與最大位移比δrm的變異系數，說明殘余位移與最大位移相關性更強。

表2 鋼筋混凝土橋墩殘余位移指標統計特征值。

將256個橋墩試件殘余位移與最大位移比δrm的計算結果繪制成直方圖及高斯分布擬合圖，如圖3所示。圖3表明，殘余位移與最大位移比δrm統計直方圖與高斯分布擬合較好。

圖3 殘余位移與最大位移比直方圖及高斯分布擬合曲線

1.3 殘余位移指標均值影響參數

為了研究基本參數對鋼筋混凝土橋墩殘余位移指標的影響規律，分別將軸壓比、剪跨比、縱筋率或箍筋率取為表1中的某一水平，統計其他參數變化情況下殘余位移指標δrh和δrm的均值。例如，在軸壓比水平為0.1時，對應橋墩試件為64個，通過對64個橋墩試件的殘余位移指標δrh和δrm的統計分析，可得到其平均值；同理，可得其他給定參數水平下各殘余位移指標δrh和δrm的平均值。表3列出了各基本參數取不同水平時殘余位移指標δrh和δrm的平均值；由表3可見，殘余位移指標δrh和δrm的平均值隨著軸壓比、剪跨比等設計參數變化趨勢相同，殘余位移比δrh的平均值在1.46%～5.32%變化，而殘余位移與最大位移比δrm的平均值在0.52～0.75變化。

表3 殘余位移指標均值

圖4～圖7顯示了軸壓比、剪跨比、縱筋率和箍筋率對殘余位移指標δrm均值的影響。由圖4和圖5可知，δrm隨軸壓比增大而減小，且隨剪跨比增大而增大；但當剪跨比大于6時，剪跨比對殘余位移指標δrm的影響趨緩。由圖6和圖7可知，δrm隨縱筋率和箍筋率增大而增大，但變化幅度均較小。采用線性回歸分析方法，應用Origin軟件擬合出殘余位移指標δrm與軸壓比等4個影響因素的關系。

圖4 軸壓比對殘余位移與最大位移比均值的影響

圖5 剪跨比對殘余位移與最大位移比均值的影響

圖6 縱筋率對殘余位移與最大位移比均值的影響

圖7 箍筋率對殘余位移與最大位移比均值的影響

表2表明，殘余位移指標δrh和δrm的統計特征值中變異系數分別為0.53和0.19，存在較大的離散性。因此，需要綜合考慮各影響因素，提高殘余位移指標能力預測的有效性。綜合考慮軸壓比等4個主要影響參數，基于256個橋墩試件樣本模擬結果，應用Origin軟件進行多元回歸分析，得到殘余位移指標δrh和δrm的概率分布模型。分別式(3)和式(4)所示

(3)

(4)

2 貝葉斯概率參數估計

2.1 貝葉斯更新理論

采用貝葉斯更新理論，可綜合考慮經驗計算公式和觀測數據存在的固有不確定性與認知不確定性，獲得橋墩殘余位移指標后驗分布概率模型。根據貝葉斯理論，若隨機變量Θ先驗分布概率密度函數為f′(θ)，通過獲取擬靜力試驗觀測數據，參數先驗分布進行更新得到后驗分布可為

f″(θ)=kL(θ)f′(θ)

(5)

擬靜力試驗結果ε為一組觀測值(x1,x2,…，xn)，該組值代表了概率密度函數為fX(x)的總體X的一個隨機樣本。似然函數L(θ)為X在(x1,x2,…，xn)處概率密度函數之積，即

(6)

假定參數服從正態分布，由式(6)可知，參數μ的似然函數為L(μ)，可表示為

(7)

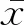
因此，參數μ的后驗分布變為

(8)

式中：μ′為先驗分布均值；σ′為先驗分布標準差。

由共軛分布可知[19]，先驗分布為正態分布，后驗分布也為正態分布，其更新后均值μ″和方差σ″表示為

(9)

(10)

2.2 試驗觀測值

Lehman等完成的815、1015和407模型橋墩截面尺寸為609.6 mm，混凝土強度為31 MPa，主筋屈服強度為462 MPa，表4列出了軸壓比等4個主要參數取值。表5為Lehman等完成的3個試件觀測結果。

表4 RC橋墩擬靜力試驗試件參數值

表5 RC橋墩擬靜力試驗觀測值

2.3 后驗分布

殘余位移指標先驗概率分布用式(3)和式(4)表示。基于表5所列3個橋墩擬靜力試驗觀測結果，采用貝葉斯更新理論推導的式(9)和式(10)，可建立殘余位移指標后驗概率分布，表示為

δrm=0.62-0.54u+0.02λ+0.03ρl+

(11)

(12)

通過對比殘余位移指標先驗概率分布與采用貝葉斯更新后殘余位移指標后驗概率分布，結果表明，殘余位移與最大位移比δrm標準差由0.10減小到0.04，殘余位移比δrh標準差由1.48減小到1.13，殘余位移指標離散性有所下降。

3 貝葉斯估計應用

為了驗證貝葉斯更新后的殘余位移指標概率分布模型估計的有效性，本文選取了5個墩柱構件擬靜力試驗結果進行驗證，表6和表7所述試件來源5個試驗數據均來源于美國太平洋地震工程研究中心的結構特性數據庫[20]。表6列出了所有試件基本參數值。采用殘余位移指標先驗分布和后驗分布可對5個擬靜力試驗構件結果進行驗證，結果如表7所示。

表6 RC橋墩擬靜力試驗試件參數值

表7 RC橋墩殘余位移指標貝葉斯估計

總體上來看，由表7可得，所有試驗構件的殘余位移指標試驗結果采用更新后的后驗分布預測準確性要優于先驗分布預測的結果；采用后驗分布對殘余位移指標預測結果與試驗結果誤差率能夠控制在10%以下，在工程可接受范圍之內。

4 結 論

(1) 在軸壓比、剪跨比、縱筋率和箍筋率4個影響因素中，軸壓比對鋼筋混凝土橋墩殘余位移指標影響最大，且殘余位移指標均值隨軸壓比的增大而減小。

(2) 鋼筋混凝土橋墩殘余位移指標均值隨剪跨比、縱筋率和箍筋率的增大而增大，但總體增加幅度不大。

(3) 建立了擬靜力作用下橋墩殘余位移指標概率模型，可用于抗震性能設計和評估時殘余位移指標估計。

(4) 基于貝葉斯更新理論，綜合利用先驗信息和擬靜力試驗觀測信息更新獲得后驗分布估計，計算更具科學性，能夠在試驗數據樣本不大的條件下估計參數的概率特性。