考慮時變嚙合剛度的多慣量伺服系統機械諧振分析及抑制方法研究
李文禮, 陸 宇, 郭 棟, 劉永康, 石曉輝, 嚴海燕
(1. 重慶理工大學 汽車零部件先進制造技術教育部重點實驗室, 重慶 400054;2. 東風汽車股份有限公司 東風商品研發院, 武漢 430056)
伺服系統是一種包括驅動電機、傳動機構、負載和控制系統的典型復雜機電系統,其中傳動機構的彈性使得系統本身存在諧振頻率[1-3]。隨著高性能伺服系統帶寬的增加,當有諧振頻率的信號作用到系統時,通常會使得系統發生機械諧振。這不僅會引起系統控制量振蕩,影響系統的控制性能和精度;還可能會損壞傳動機構、燒毀驅動電機。因此,對伺服系統機械諧振進行分析和抑制具有重要的意義。
為了抑制伺服系統的機械諧振,所使用的方法一般可分為兩種,即主動抑制方法和被動抑制方法。主動抑制方法是國內外學者研究的熱點,其原理是通過主動改變控制器參數或控制器結構來消除機械諧振,包括基于PI(proportional-integral control)的控制、基于模型預測控制(model predictive control,MPC)等高級控制算法、基于狀態觀測器的反饋控制等[3-10]。被動抑制方法主要是使用低通濾波器或陷波濾波器等來抑制機械諧振,但低通濾波器會帶來相位滯后、陷波濾波器對系統參數變化較敏感等問題,容易導致系統動態性能變差[11]。杜仁慧等在考慮與機械諧振密切相關的系統參數不確定的情況下,基于反步法設計了自適應模糊控制器,有效地抑制了系統啟動階段和負載突變時的機械諧振。楊明等針對伺服系統中由彈性軸系引起的機械諧振及軸系安全性進行研究,在雙慣量伺服系統模型基礎上,對比分析了基于PI方法和MPC方法的不同控制效果,理論分析和仿真試驗驗證了MPC方法的優越性。Wang等[12]設計了動態表面控制與加速度反饋相結合的機械諧振抑制方法,利用高階滑模加速度觀測器來估計加速度信號,引入電機加速度反饋以減小機械諧振的影響。王建敏等[13]提出了一種雙二次諧振抑制數字濾波器,能夠將諧振點和反諧振點同時抑制。龔文全等[14]使用改進型陷波濾波器進行機械諧振抑制,以減小陷波器引入的相位滯后。
現有對伺服系統機械諧振分析及抑制問題的研究,多將伺服系統簡化為雙慣量模型,忽略了傳動機構帶來的影響,如傳動間隙、齒輪嚙合過程中時變嚙合剛度等。但在實際工業應用中,傳動環節存在不確定性,這意味著并不是所有情況都可以忽略傳動機構的傳動間隙、剛度、質量等參數[15-16]。為了更精確地抑制機械諧振和控制伺服系統,對多慣量伺服系統進行建模分析很有必要。相比于雙慣量伺服系統,多慣量伺服系統模型復雜、諧振峰值不易理論推導,不適合使用被動抑制方法來抑制機械諧振。而基于MPC的主動抑制方法的預測方程不需要精確的數學模型,同時可處理各種帶約束的線性、非線性問題,理論上可以很好的用于抑制多慣量伺服系統的機械諧振問題。基于上述分析,本文考慮時變嚙合剛度對系統機械諧振的影響,首先建立四慣量伺服系統模型,并對系統的機械諧振產生機理進行分析。采用MPC方法對含時變嚙合剛度的四慣量伺服系統機械諧振進行抑制,通過仿真驗證了MPC控制器的有效性。
1 四慣量伺服系統模型及諧振分析
伺服系統在許多工業領域如數控機床、機器人、電動汽車驅動系統、高端試驗裝備以及國防工業中應用十分廣泛,其轉矩傳遞通常由多個不同的機械傳動機構完成。如圖1所示為一個典型的伺服系統結構,負載通過聯軸器、齒輪箱、傳動軸等與驅動電機相連。為了更精確地對系統機械諧振抑制進行研究,本文建立考慮時變嚙合剛度的四慣量伺服系統模型。
1.1 四慣量伺服系統
為了便于分析,忽略圖1中電機的電磁阻尼和電磁剛度、輪齒嚙合綜合誤差,將電機、齒輪箱的主被動齒輪和負載簡化為4個集中的轉動慣量元件,建立如圖2所示的四慣量伺服系統模型。該模型中電機轉軸通過齒輪副與負載連接,系統輸入為電機端電磁轉矩Te直接作用于電機轉軸,負載端傳遞轉矩Ts2與負載轉矩TL共同作用決定負載端輸出轉速,Ts1為電機轉軸與齒輪1之間的傳遞轉矩。
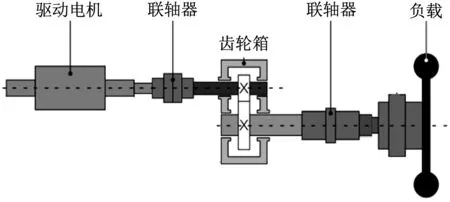
圖1 伺服系統示意圖

圖2 四慣量伺服系統模型
圖2所示的系統動力學方程可以表示為
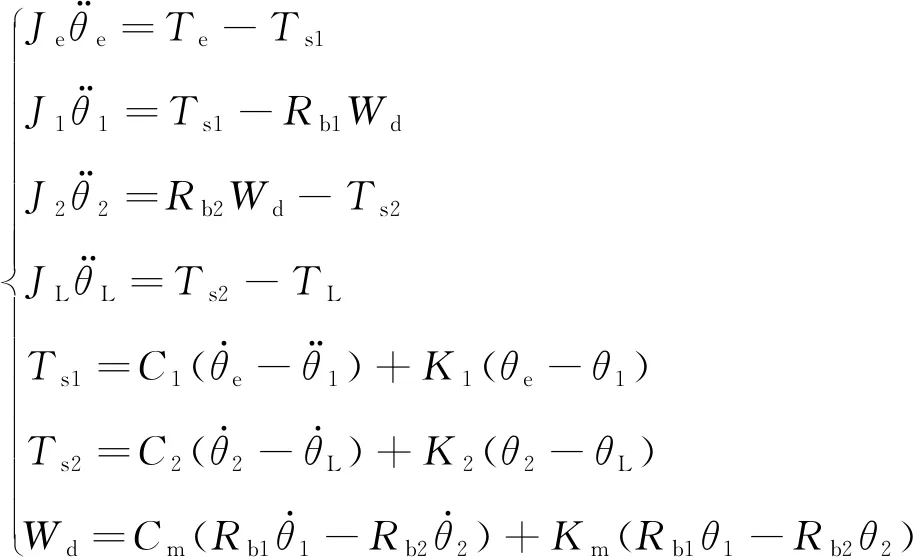
(1)
式中:θe,θ1,θ2,θL分別為等效電機軸、齒輪1、齒輪2和負載的轉角;Je,J1,J2,JL分別為電機、齒輪1、齒輪2和負載的轉動慣量;Wd為輪齒的動態嚙合力;Rb1,Rb2分別為齒輪1和齒輪2的基圓半徑;C1,C2分別為輸入軸與輸出軸的阻尼系數;K1,K2分別為輸入軸和輸出軸的剛度系數;Cm,Km分別為齒輪副的嚙合阻尼和嚙合剛度。
1.2 機械諧振分析
在實際伺服系統中,機械傳動機構由于不是理想剛體而表現出一定的彈性形變,彈性形變的存在會引起系統的機械諧振。將齒輪副的嚙合剛度等效為一個定值(即嚙合剛度為定剛度,這里取Km為5×107N/m)時,由式(1)可以得到所建立的四慣量伺服系統中輸入量電磁轉矩到輸出量電機轉速的波特圖,如圖3所示。
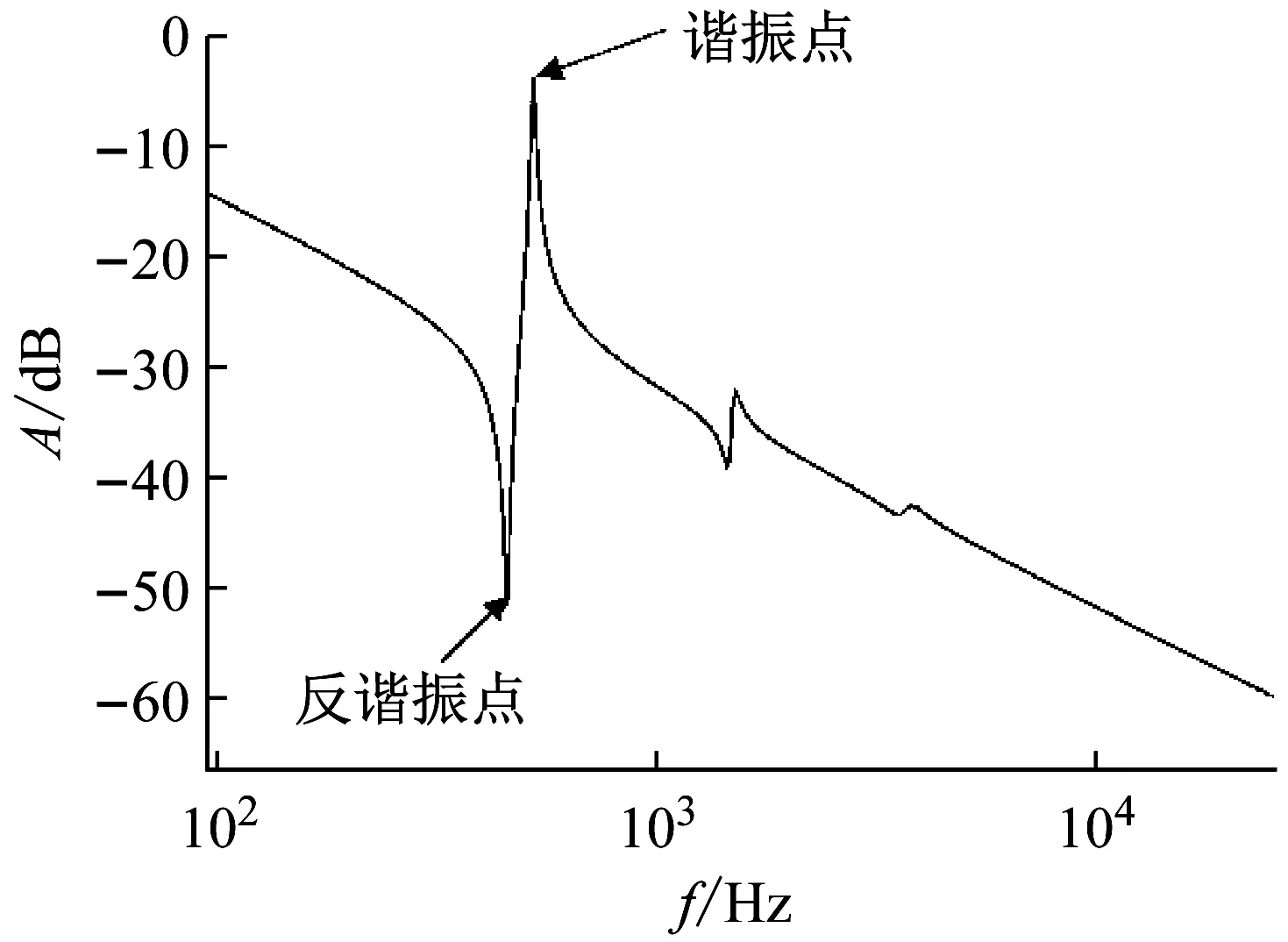
圖3 電機端轉速反饋時伺服系統波特圖
從圖3中可以看出,系統存在3對諧振點和反諧振點,即系統中輸入軸、輸出軸和齒輪副都將給系統帶來共軛零極點,進而產生與其對應的機械諧振。因此,系統電機轉速ωe和電磁轉矩Te之間的傳遞函數可以簡化表示為[17]
(2)
式中:ωbn和ωan分別為第n個諧振環節的諧振頻率和反諧振頻率;ξbn和ξan分別為第n個諧振環節的諧振阻尼系數和反諧振阻尼系數。
由式(2)可得給系統帶來機械諧振環節的傳遞函數為
(3)
對式(3)分析可知系統的諧振頻率與傳動機構的剛度系數和系統各部分等效慣量有關。
為了研究系統負載端轉速控制性能,假設嚙合定剛度分別為5×107N/m,5×108N/m和5×109N/m,系統其余參數不變,可以得到如圖4所示的不同嚙合定剛度下四慣量伺服系統中輸入電磁轉矩到輸出負載端轉速的波特圖。由圖4可知,定剛度值的變化會改變系統的諧振頻率,即系統諧振頻率值會隨著定剛度值的增加而增加。

圖4 負載端轉速反饋時伺服系統的波特圖
2 時變嚙合剛度
齒輪副嚙合剛度的變化會改變系統的諧振頻率,從而對系統機械諧振產生影響。時變嚙合剛度產生機理為在齒輪副嚙合過程中,同時參與嚙合的齒對數隨時間而周期變化,從而導致嚙合剛度隨時間變化[18]。精確估計嚙合剛度變化通常使用有限元法,但這種方法建立的模型很難加入到控制系統中。本文使用如圖5所示的時變波形來近似表示嚙合剛度值,以到達在控制系統中建模的目的。在每個嚙合周期Tsc里,當齒輪為雙齒嚙合狀態時,即(ε-1)Tsc時間段嚙合剛度為最大值,ε為重合度;當齒輪為單齒嚙合狀態時,即(2-ε)Tsc時間段嚙合剛度為最小值。
嚙合周期可以表示為
(4)
式中:Z1,Z2分別為齒輪1和齒輪2的齒數;f1,f2分別為齒輪1和齒輪2的轉動頻率。
為了確保齒輪連續平穩的傳遞動力,重合度需大于1,其表達式為
(5)
式中:Ra1,Ra2分別為齒輪1和齒輪2的齒頂圓半徑;a為齒輪1和齒輪2的標準中心距;α為壓力角;m為齒輪模數。
假設輪齒之間的接觸為赫茲接觸,輪齒的表面可以是圓形或橢圓形[19]。則最小嚙合剛度可計算為
(6)
式中:E為楊氏模量;W為齒寬;υ為泊松系數。
最大嚙合剛度為
Kmax=2Kmin
(7)
因此,時變嚙合剛度函數可以表示為

(8)
式中:λ=ε-1;ωsc=2π/Tsc。
根據本文選取的齒輪參數,如表1所示,求得重合度ε約為1.8,最小嚙合剛度Kmin約為3.35×109N/m,λ為0.8;當轉速為2 400 r/min時,輸入軸轉速頻率為40 Hz,由于輸入軸齒輪的齒數為20,齒輪的嚙合頻率為800 Hz,嚙合周期Tsc為0.001 25 s。將上述值代入式(8)可以得到如圖6所示的時變嚙合剛度值,即時變嚙合剛度最小值約為3.35×109N/m,最大值約為6.7×109N/m。

表1 伺服系統主要參數

圖6 時變嚙合剛度值
為了進一步探究時變嚙合剛度對伺服系統機械諧振的影響,首先分析時變嚙合剛度范圍內諧振頻率的變化范圍,這里取嚙合定剛度分別為時變嚙合剛度的最小值、中間值和最大值的近似值,即3×109N/m, 5×109N/m和7×109N/m,系統其余參數不變,可以得到系統輸入電磁轉矩到輸出負載端轉速的波特圖,如圖7所示。由圖7可以看出時變嚙合剛度帶來的機械諧振頻率范圍約為17 890~27 160 Hz。

(a)
然后根據式(1)建立包含時變嚙合剛度的四慣量伺服系統模型,對建立的伺服系統模型,對比分析其在嚙合剛度為時變嚙合剛度(即變剛度)和定剛度(Km為5×109N/m)情況下的機械諧振情況。當給定驅動電機為2 400 r/min的階躍指令時,圖8、圖9分別為負載端傳遞轉矩Ts2的時域波形和頻域特性。由圖8可知,在考慮變剛度參數時,系統傳遞轉矩會產生更大的波動。圖9為階躍信號穩定后的頻域特性,其中650 Hz和1 900 Hz附近產生諧振的是系統的輸入軸和輸出軸,23 100 Hz附近產生的諧振主要由齒輪副產生。可以看出變剛度系統中傳動軸產生的諧振大于定剛度系統;定剛度系統在23 100 Hz產生較大的諧振,變剛度系統在23 100 Hz諧振不大,但以該頻率為中心產生了兩個較大的諧振帶,且諧振頻率間隔為800 Hz,這與圖7分析的由時變嚙合剛度引起的機械諧振頻率范圍基本相符。從定剛度和變剛度參數下系統的諧振情況對比可以看出,在對四慣量伺服系統機械諧振分析及抑制方法進行研究時,有必要將齒輪嚙合剛度考慮為時變嚙合剛度。

圖8 定剛度和變剛度下伺服系統傳遞轉矩Ts2變化
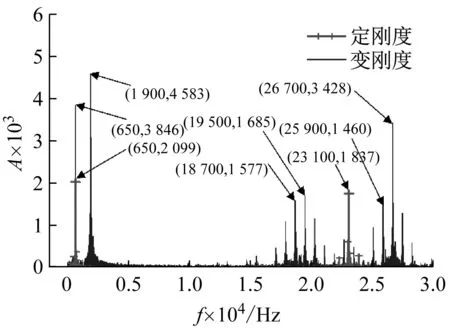
圖9 定剛度和變剛度下伺服系統的頻域特性
3 基于MPC方法的機械諧振抑制
MPC方法基本原理是根據系統的預測模型、當前時刻的狀態和未來的控制量去預測系統未來一段時域的輸出,通過滾動求解滿足目標函數和各種約束的優化問題來得到系統實際控制輸入量,從而實現控制目的[20]。為了對建立的包含時變嚙合剛度的四慣量伺服系統機械諧振進行抑制,基于MPC方法獲得系統控制輸入量Te,控制的目標是有效地抑制系統的機械諧振,同時使系統具有良好的動態性能,即系統輸出負載轉速能很好地跟蹤其參考值。如圖10所示為伺服系統MPC控制框圖,伺服系統處于速度控制模式。

圖10 伺服系統MPC控制框圖
3.1 預測模型建立
考慮齒輪嚙合剛度為時變嚙合剛度,由式(1)可以得到四慣量伺服系統的連續系統狀態空間方程
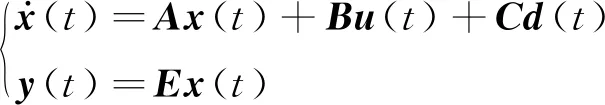
(9)



使用前向歐拉法對式(9)進行離散化處理,得到離散系統的狀態空間方程為

(10)
式中:k為當前采樣時刻;k+1為下一個采樣時刻。
3.2 目標函數設計
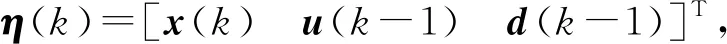

(11)
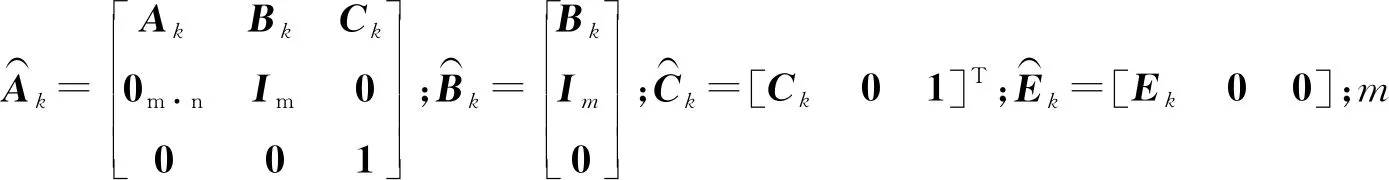
設定預測時域為Np,控制時域為Nc,Nc Y(k)=Φη(k)+ΨΔU+ΓΔD (12) 式中: 考慮系統控制目標為在不超過最大允許電磁轉矩的前提下實現負載轉速的精確跟蹤,設計優化目標函數為 (13) 式中:Yref(k+i|k)為系統輸出變量的參考值;(k+i|k)為以k時刻的系統輸出量來預測k+i時刻的值,其中i=1,2,…,Np;ΔU(k+i)為k+i時刻系統控制輸入增量,即電磁轉矩增量,其中i=0,1,…,Nc-1;Q和R為權重矩陣。 系統需要對控制輸入的電磁轉矩、電磁轉矩增量及系統輸出施加約束條件,控制輸入及其增量約束條件為 (14) 式中:umin和umax分別為電磁轉矩的最小值和最大值;Δumin和Δumax分別為電磁轉矩增量的最小值和最大值。 系統輸出約束條件為 γmin≤γ(k+i)≤γmax (15) 式中,γmin和γmax分別為系統輸出的最小值和最大值。 系統優化求解問題即在預測時域里,式(13)在滿足式(14)、式(15)的約束條件下達到最小。即在每個控制周期里需要解決以下問題 (16) 通過求解二次規劃問題,可以得到控制時域內的系統控制輸入增量為 Nc-1)]T (17) 將控制輸入增量的第一項Δu(k)取出,即可得到當前時刻系統控制輸入為 u(k)=u(k-1)+Δu(k) (18) 為了驗證MPC方法對包含時變嚙合剛度的四慣量伺服系統的機械諧振抑制的有效性,并與基于PID方法的控制效果進行比較,在MATLAB/Simulink中建立了系統仿真模型。伺服系統主要參數,如表1所示。 MPC控制器主要參數設為:預測時域Np=20,控制時域Nc=4,權重取值Q=0.1,R=1,系統控制輸入的電磁轉矩范圍|Te|≤60 N·m,系統輸出的轉速范圍|γ|≤18 000/π r/min;PID控制器參數設為:比例系數1.35,積分系數20,微分系數0.001 5。仿真時轉速階躍響應參數設為:參考轉速0~500~1 000 r/min,且在1.4 s突加30 N·m的負載轉矩。 首先對使用MPC方法和未使用MPC方法(即速度控制器中為未經優化的PI控制)時負載端轉速變化進行仿真對比,由圖11轉速階躍響應可知,當伺服系統未使用MPC方法時,伺服系統負載端轉速有很大的周期性振蕩,這是由于系統中存在的機械諧振未被有效的抑制的原因。利用MPC方法能夠減小負載端轉速的振蕩,即說明MPC能夠抑制所建立的四慣量伺服系統的機械諧振。 圖11 轉速階躍響應時負載端轉速變化(有無使用MPC方法對比) 為進一步對比驗證MPC方法的控制性能,利用MPC和PID控制方法對建立的四慣量伺服系統模型進行機械諧振抑制的仿真試驗。圖12為兩種控制方法下系統控制輸入的電磁轉矩變化,使用MPC方法時控制輸入的電磁轉矩響應時間優于PID方法,且總體上振蕩小于PID方法。圖13為階躍響應時負載端轉速變化的仿真結果,可以看出MPC方法下的響應時間和超調量均優于PID方法,其中MPC控制下的超調量約為3%、PID控制下的超調量約為12%。加入負載轉矩干擾后,MPC方法反應迅速,抗干擾能力好。圖14和圖15為階躍響應下負載端傳遞轉矩Ts2的變化曲線,由圖14和15可知,在電機啟動、加速以及負載轉矩突變時,負載端傳遞轉矩都有較大的振蕩,使用PID方法時傳遞轉矩的振蕩大于MPC方法。仿真結果說明使用MPC方法抑制機械諧振的有效性且達到了預期控制效果。 圖12 MPC和PID方法下轉速階躍響應時電磁轉矩Te變化 圖13 MPC和PID方法下轉速階躍響應時負載端轉速變化 圖14 MPC和PID方法下轉速階躍響應時傳遞轉矩Ts2變化 圖15 MPC和PID方法下轉速階躍響應時傳遞轉矩Ts2變化(局部放大圖) 機械諧振抑制對提高伺服系統的控制品質具有重要意義,本文為了更深入的研究多慣量伺服系統振動的機理、提高伺服系統的控制性能,主要做了以下工作。 (1) 考慮齒輪副時變嚙合剛度對伺服系統機械諧振的影響,建立了由電機、主被動齒輪和負載組成的四慣量伺服系統模型,分析了系統機械諧振的產生機理,對比了有無齒輪時變嚙合剛度的伺服系統模型機械諧振表現特征,以此說明考慮齒輪時變嚙合剛度可使仿真模型更逼近真實系統。 (2) 基于包含齒輪時變嚙合剛度的四慣量伺服系統模型設計了模型預測控制器,驗證了MPC方法對考慮齒輪時變嚙合剛度模型的諧振抑制的有效性,并與PID方法的控制性能進行了對比。 (3) 仿真結果表明,在轉速階躍響應中,MPC方法能有效抑制系統機械諧振的影響,其控制效果優于PID方法。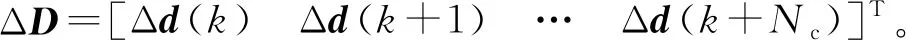

3.3 約束條件設計

3.4 優化求解
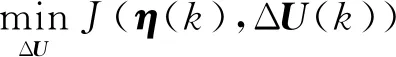



4 仿真及結果分析
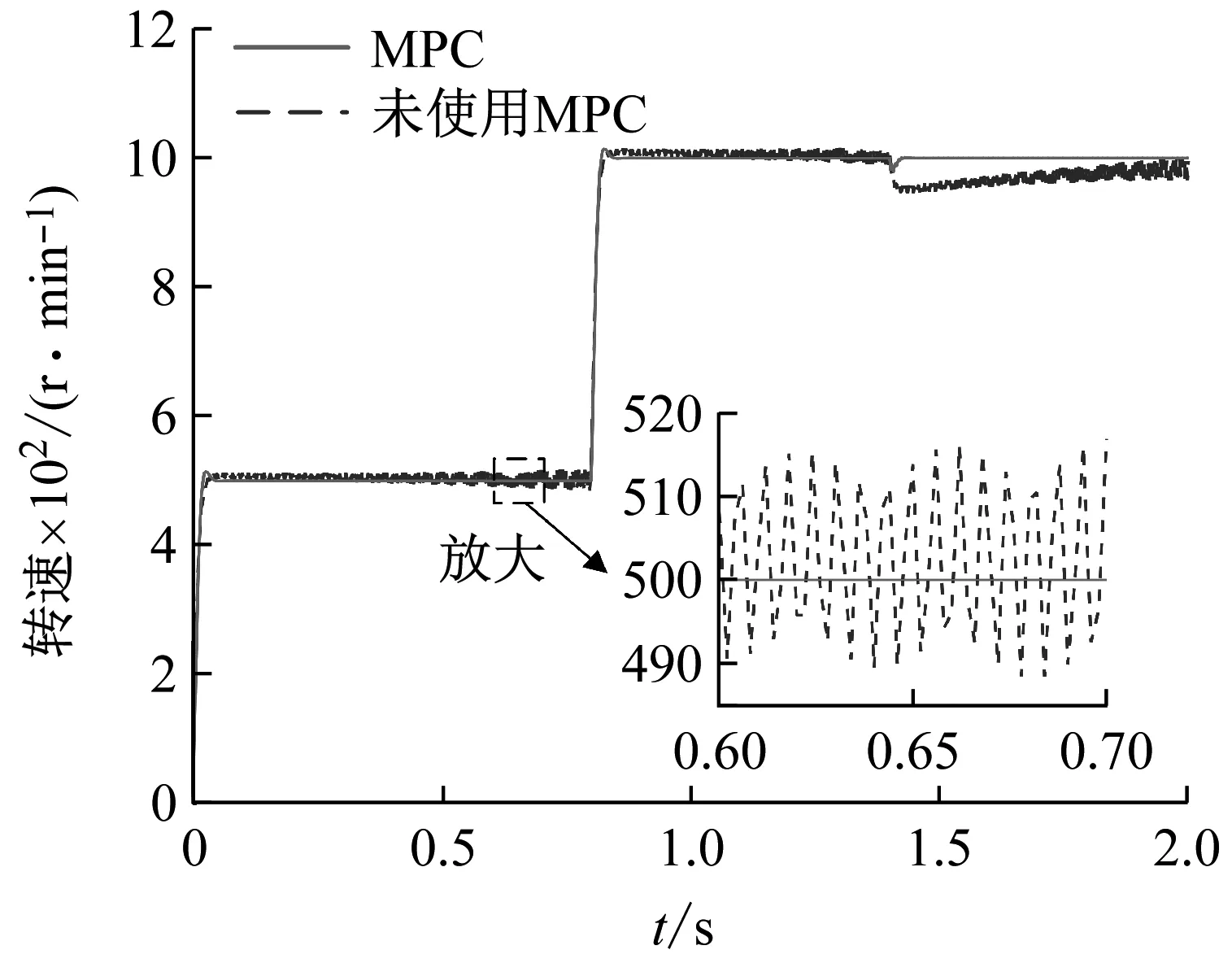
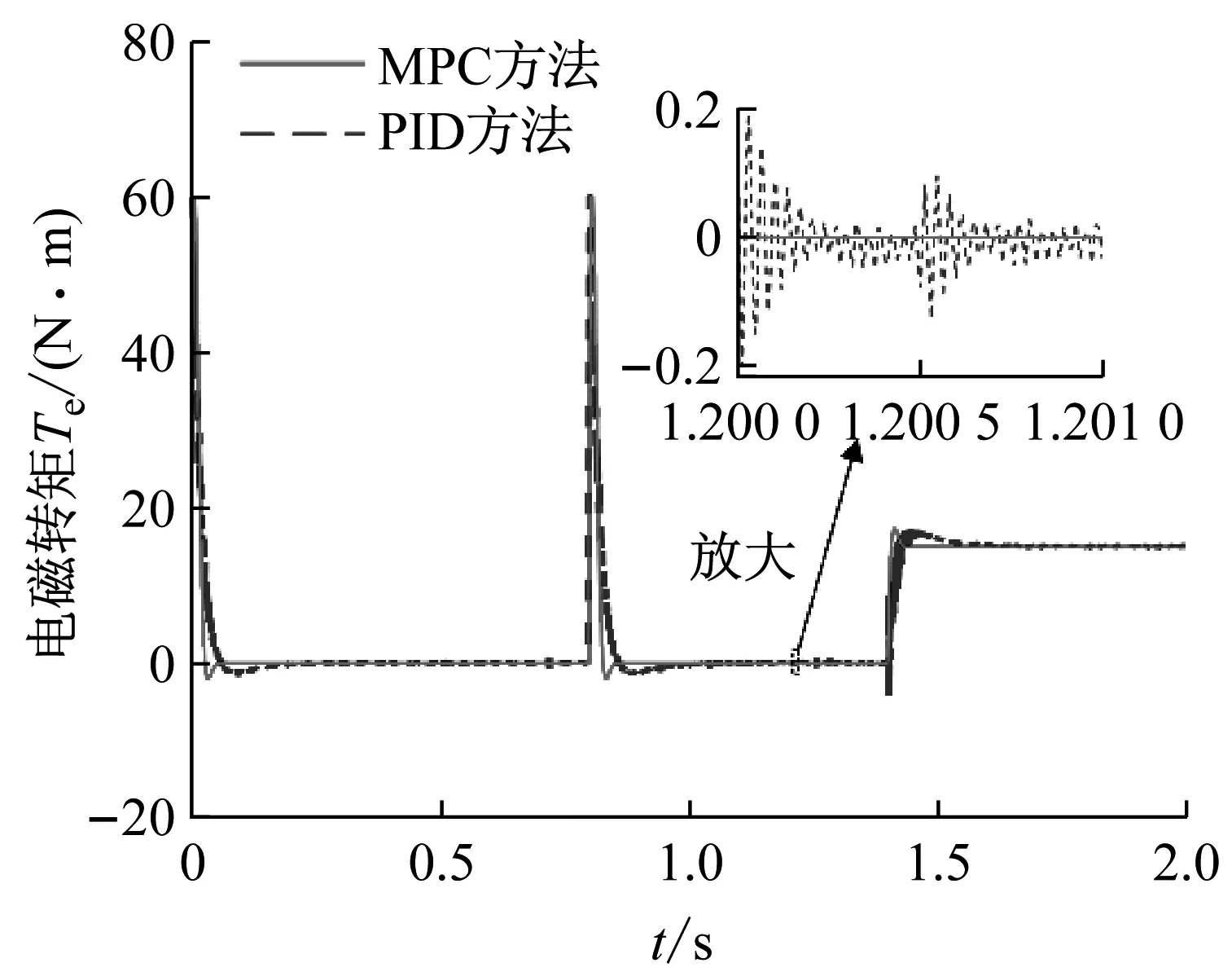
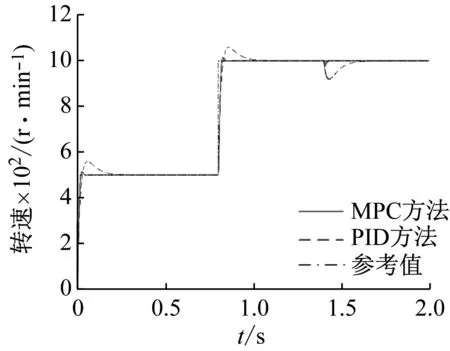


5 結 論

