時(shí)滯非線性參數(shù)系統(tǒng)有限時(shí)間狀態(tài)約束控制
金 璇,劉文慧
(南京師范大學(xué)南瑞電氣與自動(dòng)化學(xué)院,江蘇 南京 210023)
近年來(lái)非線性系統(tǒng)的控制問(wèn)題引起了廣泛的關(guān)注,許多有效的控制方法陸續(xù)被提出,例如滑模控制[1]、模糊控制[2]、魯棒控制和自適應(yīng)控制[3-6]. 自適應(yīng)反步控制法[7-8]可以根據(jù)系統(tǒng)本身的狀態(tài),構(gòu)造保證系統(tǒng)存在不確定性時(shí)仍具有強(qiáng)魯棒性的結(jié)構(gòu),因此被廣泛用于穩(wěn)定非線性系統(tǒng)[9-11]. 眾所周知,參數(shù)不確定的非線性自適應(yīng)控制也是非線性控制設(shè)計(jì)中的熱點(diǎn)問(wèn)題,自適應(yīng)反步技術(shù)被廣泛用來(lái)解決不確定非線性系統(tǒng)的控制問(wèn)題[12-15]. 然而參數(shù)化非線性系統(tǒng)狀態(tài)約束和有限時(shí)間控制問(wèn)題鮮有研究.
工業(yè)實(shí)際應(yīng)用中存在各種各樣的物理?xiàng)l件約束,例如機(jī)械臂系統(tǒng)中位置和速度的限制[16],連續(xù)攪拌釜反應(yīng)器中溫度和壓力的限制[17]等,系統(tǒng)狀態(tài)約束成為一個(gè)具有挑戰(zhàn)性的熱點(diǎn)問(wèn)題. 近來(lái),構(gòu)造Barrier Lyapunov函數(shù)使系統(tǒng)狀態(tài)被約束在給定區(qū)域內(nèi)的方法得到大量應(yīng)用[18-19]. 另一方面,不同于漸近穩(wěn)定理論,有限時(shí)間穩(wěn)定能夠保證系統(tǒng)內(nèi)的變量在有限時(shí)間內(nèi)快速收斂于平衡點(diǎn),使系統(tǒng)擁有更好的瞬態(tài)特性. 對(duì)于大多數(shù)工程應(yīng)用,需要系統(tǒng)在有限時(shí)間內(nèi)達(dá)到期望性能,因此有限時(shí)間控制格外重要. 近年,有限時(shí)間控制問(wèn)題取得了巨大的進(jìn)展,許多新的控制方法應(yīng)運(yùn)而生[20-21].
由于測(cè)量和計(jì)算等的延遲,輸入時(shí)滯現(xiàn)象常見(jiàn)于化工生產(chǎn)、生物反應(yīng)器等工業(yè)生產(chǎn)中,因此許多研究輸入時(shí)滯的文獻(xiàn)應(yīng)運(yùn)而生[22-24]. 然而研究全狀態(tài)約束系統(tǒng)的輸入時(shí)滯問(wèn)題的文獻(xiàn)還比較少. 在此基礎(chǔ)上,本文研究了具有輸入時(shí)滯不確定非線性系統(tǒng)的有限時(shí)間全狀態(tài)約束跟蹤控制問(wèn)題. 設(shè)計(jì)過(guò)程中利用Barrier Lyapunov函數(shù)和pade近似法解決了狀態(tài)約束和輸入時(shí)滯問(wèn)題,再利用反步控制技術(shù)和有限時(shí)間控制方法設(shè)計(jì)了一個(gè)新的自適應(yīng)控制器. 本文主要貢獻(xiàn)為:
(1)在有限時(shí)間控制系統(tǒng)中引入全狀態(tài)約束并在反步設(shè)計(jì)過(guò)程中使用Barrier Lyapunov函數(shù)使系統(tǒng)內(nèi)所有的狀態(tài)都不超過(guò)給定的范圍;
(2)在全狀態(tài)約束非線性系統(tǒng)中考慮了輸入時(shí)滯并使用pade近似法解決其對(duì)系統(tǒng)性能的負(fù)面影響;
(3)在系統(tǒng)含有未知參數(shù)時(shí),會(huì)給系統(tǒng)帶來(lái)性能的惡化甚至導(dǎo)致系統(tǒng)不穩(wěn)定. 為了消除其負(fù)面影響,需要應(yīng)用新的自適應(yīng)控制方法,這給控制器的設(shè)計(jì)帶來(lái)困難. 而本文在控制器設(shè)計(jì)過(guò)程中,根據(jù)控制結(jié)果所需為系統(tǒng)的未知參數(shù)設(shè)計(jì)了合適的自適應(yīng)律,再利用自適應(yīng)反步技術(shù)為參數(shù)化非線性系統(tǒng)設(shè)計(jì)了新的有限時(shí)間自適應(yīng)跟蹤控制器,使閉環(huán)系統(tǒng)內(nèi)的所有信號(hào)能在有限時(shí)間內(nèi)有界,同時(shí)輸出信號(hào)追蹤給定參考信號(hào)的追蹤誤差很小.
1 問(wèn)題描述
考慮如下參數(shù)化非線性嚴(yán)格反饋系統(tǒng)
(1)

為對(duì)系統(tǒng)(1)進(jìn)行跟蹤控制器設(shè)計(jì)和穩(wěn)定性分析,需要做出如下假設(shè)并且使用如下引理.

假設(shè)2存在常數(shù)ρi>0是外部擾動(dòng)di的上界,即|di|≤ρi.
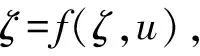
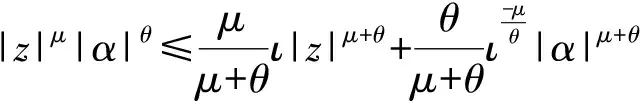
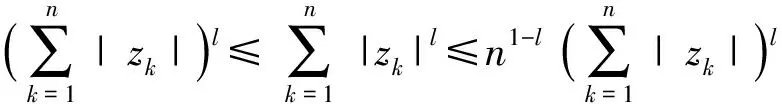
本文的控制目標(biāo)是設(shè)計(jì)一個(gè)有限時(shí)間跟蹤控制器,保證系統(tǒng)的輸出y(t)能夠跟蹤給定的參考信號(hào)yr(t),保證所有狀態(tài)不超過(guò)給定的范圍且閉環(huán)系統(tǒng)中的所有信號(hào)在有限時(shí)間內(nèi)有界.
2 跟蹤控制器設(shè)計(jì)與穩(wěn)定性分析
我們運(yùn)用自適應(yīng)反步技術(shù)和有限時(shí)間控制理論針對(duì)系統(tǒng)(1)進(jìn)行跟蹤控制器設(shè)計(jì),再使用李雅普諾夫分析法進(jìn)行系統(tǒng)的穩(wěn)定性分析.
2.1 跟蹤控制器設(shè)計(jì)
這一部分利用自適應(yīng)反步法進(jìn)行控制器設(shè)計(jì),設(shè)計(jì)過(guò)程分為n步. 為了處理帶有時(shí)滯的輸入項(xiàng)u(t-τ),本文引入pade近似法[28],系統(tǒng)(1)可重新表示為
(2)
式中,γ是待設(shè)計(jì)參數(shù),xn+1是增加的中間變量.
首先進(jìn)行如下坐標(biāo)變換
(3)
式中,e1是跟蹤誤差,vi-1和vn-1是待設(shè)計(jì)的虛擬控制器.
第1步:對(duì)跟蹤誤差e1=x1-yr求導(dǎo)得
(4)
構(gòu)建如下含有Barrier函數(shù)的Lyapunov函數(shù):
(5)
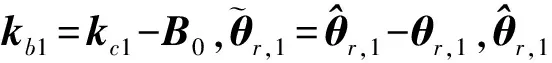
(6)
設(shè)計(jì)虛擬控制器為:
(7)
代入式(6)中得到:
(8)
根據(jù)Young不等式,得到:
(9)
(10)
令自適應(yīng)律為
(11)
則得到不等式:
(12)
式中,φr,1(x1)=φ1(x1).
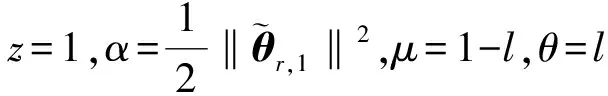
(13)
根據(jù)不等式(9)、(10)、(12)和(13),式(8)可以重寫(xiě)為
(14)
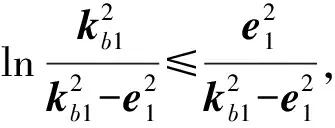
(15)
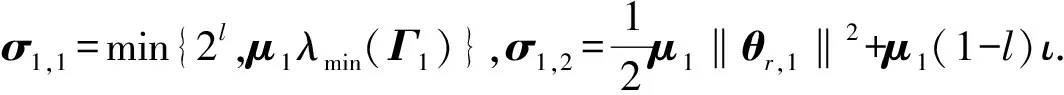
注1在設(shè)計(jì)Lyapunov函數(shù)時(shí)加入了Barrier函數(shù),使?fàn)顟B(tài)x1被限定在預(yù)定范圍內(nèi). 在接下來(lái)的步驟中,我們用了同樣的方法來(lái)確保狀態(tài)約束能夠滿足.
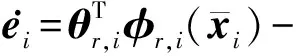
(16)
式中
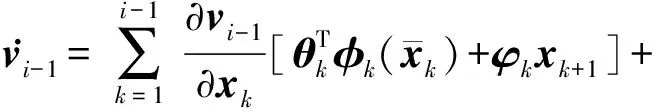
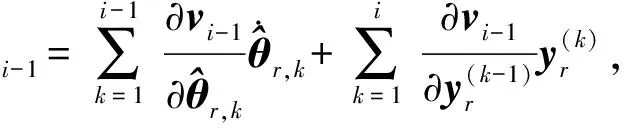
與第1步相似,構(gòu)造如下Lyapunov函數(shù):
(17)
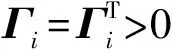
(18)
設(shè)計(jì)虛擬控制器和自適應(yīng)律為
(19)
(20)
式中,μi>0(i=1,2,…,n)是待設(shè)計(jì)參數(shù).
(21)
根據(jù)第1步中的步驟可得:
(22)
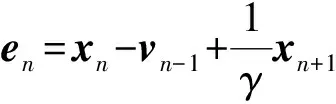
采用離散余弦變換(Discrete Cosine Transform,DCT)求解,將解纏過(guò)程轉(zhuǎn)換為采用DCT求解泊松方程的問(wèn)題,即可恢復(fù)InSAR真實(shí)相位.
(23)
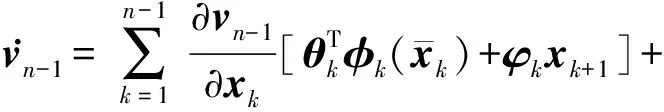
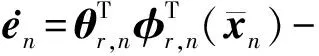
(24)
式中
設(shè)計(jì)實(shí)際控制器和自適應(yīng)律為
(25)
(26)
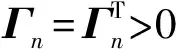
2.2 穩(wěn)定性分析
本節(jié)給出以下定理來(lái)說(shuō)明本文的主要結(jié)果. 如下文所示是有限時(shí)間穩(wěn)定的證明.
定理1對(duì)于具有輸入時(shí)滯、有界外部干擾和全狀態(tài)約束的的嚴(yán)格反饋參數(shù)化非線性系統(tǒng)(1),如果在假設(shè)1和假設(shè)2下使用控制器(25),則該閉環(huán)系統(tǒng)是半全局有限時(shí)間穩(wěn)定的.
證明設(shè)計(jì)如下Lyapunov函數(shù):
(27)
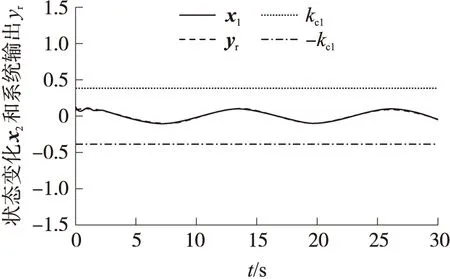
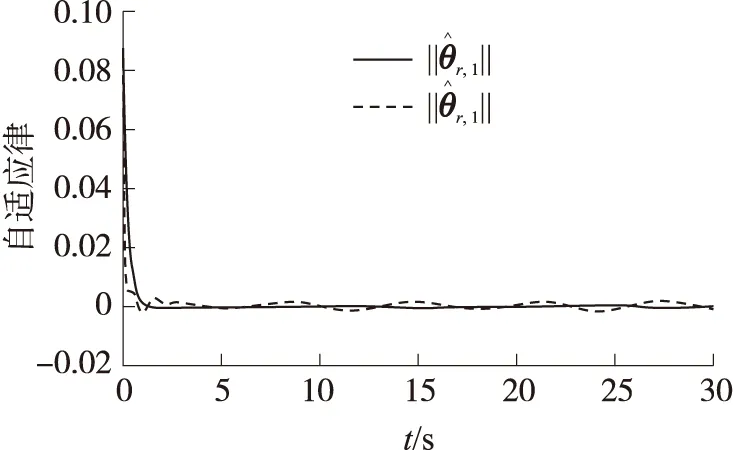
式中,kbn之后會(huì)給出. 在集合Ωen={en:|en| (28) 類似于之前的步驟,將實(shí)際控制器u和自適應(yīng)律代入可以得到: (29) 定義V=V1+V2+…+Vn且應(yīng)用引理3得到: (30) 所以根據(jù)引理1,可以得到系統(tǒng)(1)是半全局有限時(shí)間穩(wěn)定. 注2根據(jù)以上證明,顯然|x1|≤|e1|+|yr(t)| 考慮如下非線性系統(tǒng): (31) 式中,u和y是系統(tǒng)的輸入和輸出,θ1和θ2是未知常數(shù)向量. 在仿真中選擇θ1=0.1,θ2=[0.2,1]T,外部擾動(dòng)為d1=0.02cos(0.5t),d2=0.06sin(t+0.25),輸入延遲選擇為τ=0.1. 仿真結(jié)果如圖1-圖4所示. 圖1表示系統(tǒng)輸出信號(hào)y與跟蹤信號(hào)yr的軌跡,圖2表示跟蹤誤差e1的仿真結(jié)果. 由圖1和圖2可以看出系統(tǒng)跟蹤性能良好且系統(tǒng)狀態(tài)x1不超出預(yù)定界限. 圖3表示系統(tǒng)狀態(tài)x2保持在預(yù)定界限內(nèi). 圖4表明自適應(yīng)律是有界的. 以上結(jié)果都證明本文提出的新的跟蹤控制器能夠在有限時(shí)間內(nèi)使系統(tǒng)達(dá)到預(yù)期. 圖1 y(t)和yr(t)的軌跡Fig.1 Trajectories of y(t)and yr(t) 圖2 誤差e1的軌跡Fig.2 Trajectory of error e1 圖3 x2(t)的軌跡Fig.3 Trajectory of x2(t) 圖4 自適應(yīng)律和的軌跡Fig.4 Trajectories of adaptive laws 本文針對(duì)具有輸入時(shí)滯、有界外部干擾和全狀態(tài)約束參數(shù)化非線性系統(tǒng)設(shè)計(jì)了一種新的有限時(shí)間自適應(yīng)追蹤控制器. 為了消除輸入遲滯的影響,使用了pade近似法. 應(yīng)用一些的引理確保系統(tǒng)能在有限時(shí)間內(nèi)達(dá)到預(yù)期效果. 此外,利用自適應(yīng)反步技術(shù)和Barrier Lyapunov函數(shù)推導(dǎo)出自適應(yīng)控制器使系統(tǒng)輸出信號(hào)追蹤給定參考信號(hào)并保證系統(tǒng)狀態(tài)被約束在給定區(qū)域內(nèi)且保證系統(tǒng)所有信號(hào)都在有限時(shí)間內(nèi)有界. 最后,通過(guò)仿真實(shí)例驗(yàn)證了本文提出的控制器的有效性.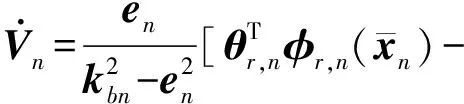
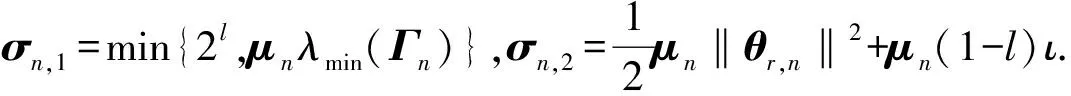
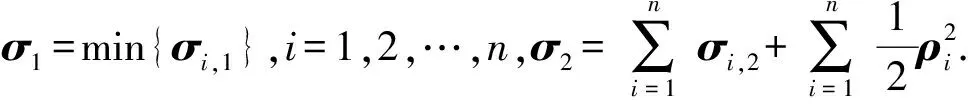
3 仿真算例
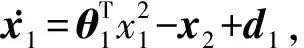


4 結(jié)論

