高溫高壓條件下納米材料強度的測試和分析方法

顧超，王善民，趙予生*

1 南方科技大學物理系，深圳 518055 2 南方科技大學前沿與交叉科學研究院，深圳 518055

0 引言

納米晶材料是由納米尺寸(<100 nm)晶粒所組成的材料.當晶體材料的晶粒大小或外形尺寸與特定的物理量相當時，如平均自由程、位錯體積、鐵磁疇、鐵電疇或聲子相干長度等，相應的物理現象將會發生明顯的變化.因此，通過控制晶粒尺寸對晶體材料進行微觀結構調控，有望產生新現象和行為，實現材料在性能上的革新.除了尺寸因素，納米晶材料在微觀結構上也不同于微晶材料，納米晶體通常可以用核-殼(core-shell)模型來描述，即包括晶格完美的晶核部分和“無序”的表面原子層，其原子排列既不同于有序的晶態，也不同于無序的非晶態(玻璃態).當晶粒尺寸減小到納米級時，殼層可占整個材料的50%甚至更多，由于納米表層的原子構造和原子之間的鍵等都與完美晶體不同，其性能也不同于晶體或非晶體，因此，可通過尺寸效應對材料的性能進行調節.大量的實驗研究表明，隨著晶粒尺寸從微米減小到納米級，材料的各種性能，如相穩定性(Chen et al.，1997)、熔化溫度(Goldstein et al.，1992)、屈服強度(Chen et al.，2005；Wang et al.，2007)、彈性模量(Tolbert and Alivisatos，1995；Jiang et al.，1998；Wang et al.，2003，2004)、電子結構(van Buuren et al.，1998)等都會發生明顯的改變.

目前，利用傳統的力學測試方法難以研究納米材料的變形機理和本征力學性能.以納米晶材料的硬度研究為例，根據經典的Hall-Petch關系(Hall，1951；Petch，1953)，可以預測多晶材料的強度隨著晶粒尺寸的減小而增加.雖然這種關系是根據經驗建立起來的，但它在許多納米晶體金屬和合金中得到了驗證(Chen et al.，2005；Qian et al.，2005；Zhao et al.，2007).Hall-Petch效應一般歸因于位錯在晶界處的塞積阻礙了塑性變形過程，使后續的位錯運動需要更大的應力來開動，從而導致硬度等力學性能的提升.因此，在晶粒尺寸較小的材料中，晶界密度的增加會對位錯運動造成更大的阻礙，宏觀表現為強度或硬度的增加.然而，實驗和分子動力學模擬結果表明(Chokshi et al.，1989；Lu et al.，1990；Palumbo et al.，1990；Chang et al.，1992；Khan et al.，2000)，在一些晶粒尺寸在3～20 nm范圍內的金屬和合金中，Hall-Petch關系并不適用.在這些材料中，當晶粒尺寸小于某一臨界值時，硬度隨著晶粒尺寸的減小而減小或保持不變，這種現象被稱為反Hall-Petch效應.在一些情況下，實驗觀察到的反Hall-Petch效應可能并非是材料的本征性能，而是由于孔隙或夾雜物的存在使材料的強度或硬度下降.其中，屈服強度并不是材料的固有特性，它取決于材料的內部結構、化學成分以及加載條件.在納米材料中，特定的化學組分或缺陷密度分布的差異，可以極大地改變材料的屈服強度.在具有高脆性和低韌性的陶瓷材料中，傳統的壓痕和拉伸試驗方法都不適合研究陶瓷材料的尺寸效應，對本征納米效應和變形機制的研究也十分匱乏.此外，對于三軸加載下納米晶材料塑性變形的位錯形核、擴展和塞積過程，以及它們隨壓力和溫度的變化趨勢，仍然沒有很好的方法可以進行表征.

通過衍射峰寬分析材料的應變或強度是科學界廣泛使用的一種經典方法，通常被稱為Williamson-Hall法或其演化法(Williamson and Hall，1953；Gerward et al.，1976).該方法可以克服傳統壓痕或變形實驗中常見的樣品孔隙或雜質問題.一般來說，多晶衍射圖譜是儀器參數、晶粒尺寸分布和晶格沿衍射矢量方向變形的卷積函數.在高壓壓縮實驗中，衍射峰的寬化表明沿著衍射矢量方向的非均勻應變的分布(Weidner et al.,1994a)，這些應變源于不同晶體取向的晶粒在受力方向上的形變，以及在粉末壓縮實驗中晶粒間接觸位置的應力集中.當偏應力接近屈服強度時，試樣開始塑性流動，衍射峰寬度達到最大值.通過分析不同的hkl晶面衍射峰寬隨壓力的變化，可以得到不同的應變值，進而得到樣品的屈服強度.基于以上方法，為了更好地理解納米材料的力學性能和變形機理，尤其是在高溫高壓下的變形行為，我們進行了一系列的同步輻射X射線衍射和中子衍射實驗來研究納米材料的本征特性.為了準確地表征納米材料的獨特性能，我們使用相同的技術研究了納米晶和微米晶材料，并在某些情況下，將這兩種材料在同一個高溫高壓實驗中進行直接比較.本文使用的方法可以用于巖石礦物的高溫高壓流變強度的定量測定，通過該方法測定的流變實驗結果可以為評估中上地殼流變結構，與發生在中上地殼的地震及其余震深度分布規律提供實驗數據支持，為反映大陸中上地殼的真實情況提供新的研究方法，為研究巖石圈以及地幔物質的蠕變對流提供了高科技的研究手段.

1 材料與方法

鎳(Ni)是一種具有重要技術意義的3d過渡金屬.納米晶Ni一直是許多實驗和理論工作的重點研究載體.在前期的研究中，納米晶Ni的力學、電學、磁性、彈性和擴散系數等性質已經得到了廣泛的研究(Bonetti et al.，1999;Chen et al.，2000；Rekhi et al.，2001；Budrovic et al.，2004；Shan et al.，2004).本研究選用微米晶和納米晶Ni粉為研究對象，微米晶Ni粉的純度為99.8%，粒度分布為3～7 μm，納米晶Ni粉是通過將商業微米晶Ni粉(Alfa Aesar, 99.999%)進行高能球磨制備的.球磨時將5 g鎳粉和30個質量為1 g的淬火鋼球放入球磨罐，用SPEX 8000球磨機研磨30小時.球磨過程是在具有氬氣環境的手套箱中操作的，手套箱中氧氣含量小于1×10-6.通過差示掃描量熱法(Differential Scanning Calorimetry，DSC)(Shen et al.，1995)測定居里轉變溫度表明，制備的納米晶Ni中含有約1 at%的鐵雜質.根據X射線衍射峰寬分析，納米晶Ni粉的平均晶粒尺寸為12～13 nm.兩種Ni粉的中子衍射譜在布拉格角為40°、90°和150°位置均未發現擇優取向.高壓X射線衍射實驗是在美國布魯克海文國家實驗室的國家同步光源X17B2線站上進行的.實驗選擇六面頂壓砧裝置對樣品進行加壓和升溫(Weidner et al.，1992)，為了進行對比實驗，納米晶和微米晶Ni被放置在同一個氮化硼管中，中間由NaCl隔開.除了隔離樣品，NaCl也同時作為內標壓物質，通過Decker狀態方程對NaCl進行壓力標定(Decker，1971).常壓下的飛行時間中子衍射實驗(time-of-flight, TOF)是在美國洛斯阿拉莫斯國家實驗室HIPPO(High-Pressure Preferred Orientation)光束線上進行的(Wenk et al.，2003).

2 納米晶材料的力學性能測試與分析

2.1 納米晶Ni的彈性軟化

在目前對納米晶材料的性能研究中，晶粒尺寸對材料彈性性能的影響仍然是一個有爭議的問題.例如，在早期的研究中發現，納米晶材料的楊氏模量值遠遠低于與之對應的微米晶材料(Gleiter，1989).盡管這種軟化現象在一定程度上可以歸因于制備的材料中存在較大體積分數的孔隙和微裂紋，但隨后基于無孔隙納米晶樣品的實驗和理論計算(Shen et al.，1995)結果仍然表明，當晶粒尺寸小于20 nm時，材料顯示出了明顯的彈性軟化現象.與之相反，在一些使用X射線衍射進行表征的壓縮實驗中，納米晶材料的體彈模量高于常規微米晶材料(Tolbert and Alivisatos，1995；Jiang et al.，1998;Wang et al.，2003，2004).此外，在Fe、Ni、MgO和CuO等材料中，壓縮性能又顯示出了與晶粒尺寸無關的現象(Chen et al.，2000；Rekhi et al.，2001；Zhang et al.，2007；Chen et al.，2008).以上研究結果表明，晶粒尺寸對材料彈性性能的影響可能不存在一個普適性的規律，其中一些研究的結論可能是不確定的.原因有兩方面，一方面是這些實驗研究大多只關注納米晶材料本身，并沒有與早期研究的常規材料數據進行對比，從而忽略了不同測試技術中系統誤差造成的影響；另一方面，納米晶的彈性變形行為過于微小，無法用常規的實驗方法來檢測.為了解決這些問題，我們利用同步輻射X射線衍射對裝載在同一腔體內的納米晶和微米晶Ni進行了高壓壓縮性能研究(Zhang et al.，2007).這種方法可以消除儀器響應和壓力/偏應力測定所產生的系統誤差，從而可以檢測出二者在壓縮過程中的微小差異(Hazen，1993；Zhang et al.，2013).

納米晶和微米晶Ni在常壓和7.4 GPa(實驗的最高壓力)下的X射線衍射(XRD)圖譜如圖1所示.由于在高能球磨細化晶粒過程中引入了表面應變效應，納米晶Ni的晶格常數略大于微米晶Ni的.此外，球磨過程引入的Fe雜質也會使衍射峰向更大的d值方向偏移(McKeehan，1923).從圖1中可以看出，納米晶Ni的衍射峰明顯比微米晶Ni的衍射峰寬.這種寬化一方面來自于晶粒細化，另一方面源于球磨過程中產生的位錯導致晶體中缺陷密度增加，從而引入了微觀晶格應變.

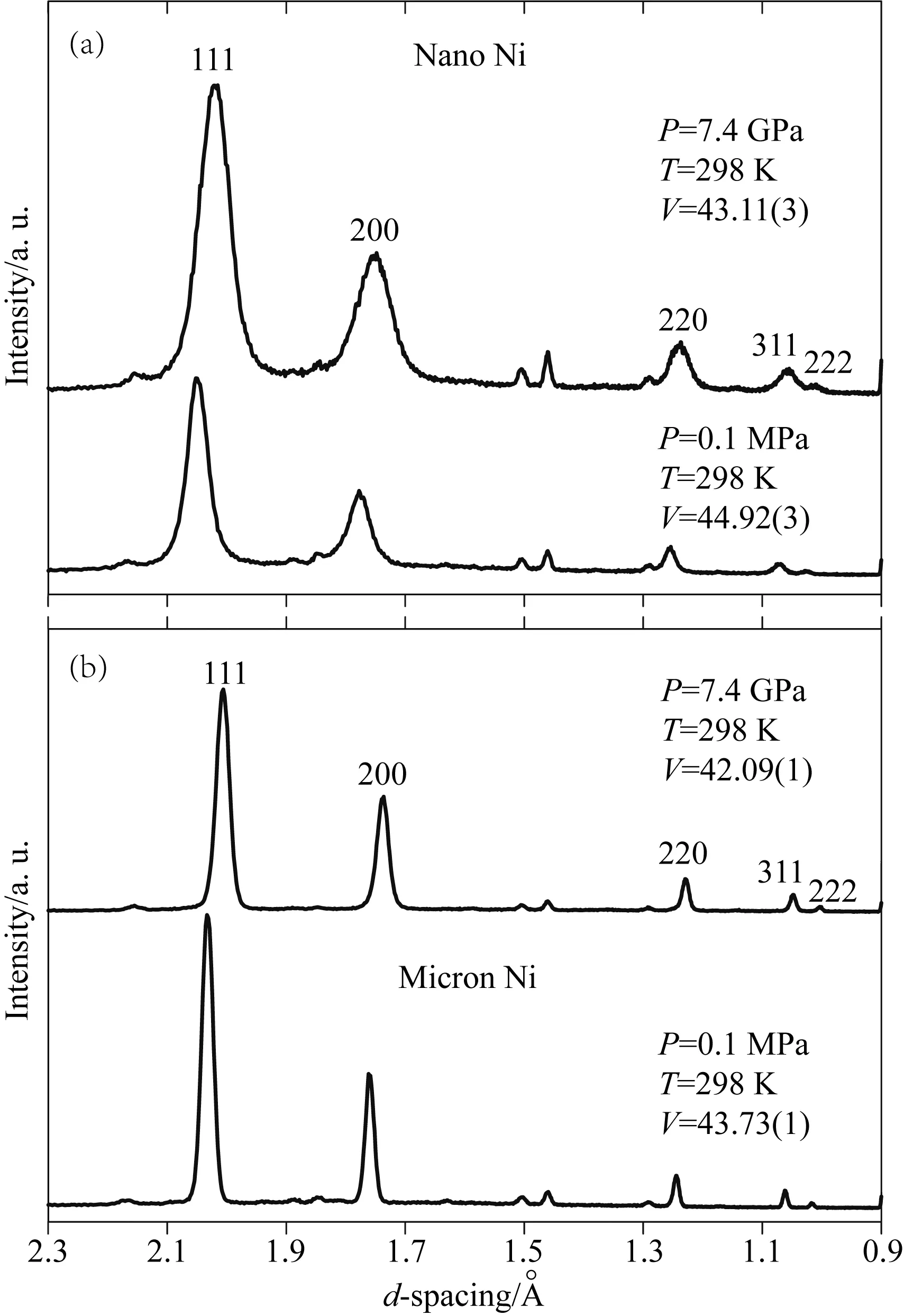
圖1 (a)納米和(b)微米Ni在298 K和選定壓力下的X射線衍射圖譜

利用實驗得到的衍射圖譜，首先通過衍射峰強度的高斯擬合確定了衍射峰位置，然后利用納米晶和微米晶Ni的111、200、220、311和222衍射峰，基于立方晶胞的最小二乘法擬合計算得出了納米晶和微米晶Ni的單胞體積(V)，其標準偏差分別為0.05%～0.1%和0.02%～0.03%.納米晶和微米晶Ni的晶胞壓縮率V/V0(V0為常壓下的晶胞體積)隨壓力變化的趨勢如圖2所示.從圖2中可以看出，納米晶Ni比微米晶Ni的抗壓縮性能更差.

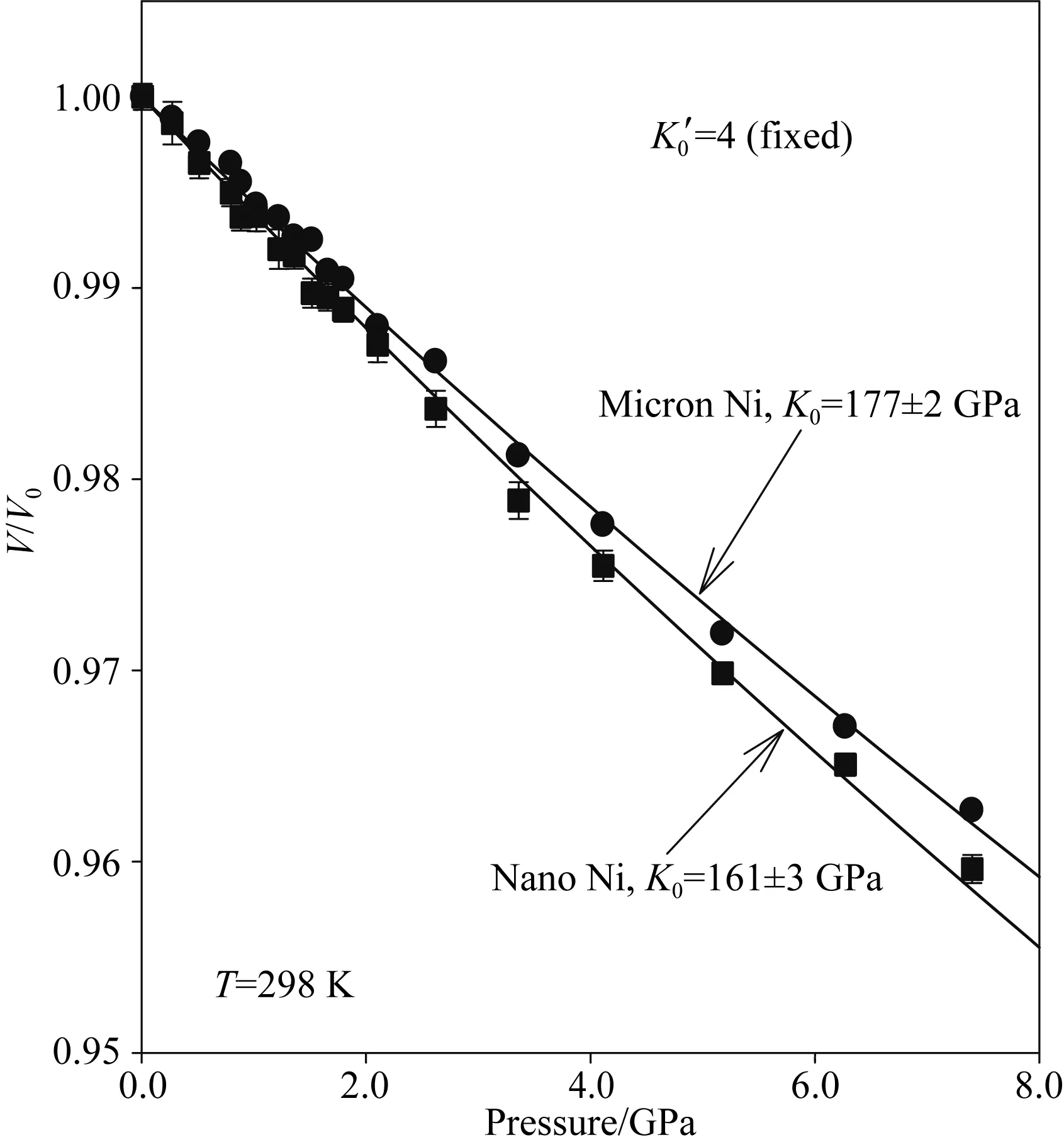
圖2 歸一化單胞體積V/V0隨壓力的變化關系

為了對二者的體彈模量進行定量比較，使用歐拉有限應變狀態方程(Birch，1978)對圖2的數據進行擬合.在狀態方程中，壓強P可表示為應變f的三階方程：

P=3f(1+2f)5/2·K0[1-2ξf+…]，

(1)

其中，

式中，K0和K′0分別為絕熱體彈模量及其在環境溫度下關于壓力的導數.由于本實驗壓力范圍有限，對K′0影響較小，故可采用二階狀態方程對體彈模量進行計算，即式(1)中ξ= 0.此時對圖2所示數據進行擬合，可得納米晶和微米晶Ni的體彈模量分別為K0=161±3 GPa和K0=177±2 GPa.該結果表明，納米晶Ni比微米晶Ni的可壓縮性高約10%.

在早期的研究中，Chen等(2000)利用X射線衍射和金剛石對頂砧技術研究了納米晶Ni的壓縮性能，根據晶格體積從常壓到55 GPa的變化趨勢，計算得出納米晶Ni的體彈模量為185.4±10 GPa，與之前報道的微米晶Ni的體彈模量180 GPa接近.在另一項研究中，Rekhi等(2001)通過實驗和第一性原理計算分別得到了納米晶Ni(K0=228±15 GPa)和微米晶Ni(K0=217 GPa)的體彈模量，結果表明二者數值相當.與我們目前的實驗結果不同，這兩項研究都得出晶粒尺寸對Ni的壓縮性能沒有影響.然而，無論在實驗或理論計算中，都會有系統誤差存在，在對不同方法得到的體彈模量數值進行比較時，由于系統誤差的影響，會增加結果的不確定性.本研究采用的實驗方法可以消除壓力和偏應力這兩個變量的誤差，更適用于壓縮性能中細微差異的檢測.

納米晶材料由于表層原子密度降低，壓縮性通常會增加(Gleiter，1989；Trapp et al.，1995).然而，到目前為止，基本沒有關于納米晶表面原子排列的具體信息，也沒有實驗方法可以直接區分表面區域和晶體內部之間的壓縮行為.Palosz等(2002)在一系列研究中表明，對于納米晶材料，很難從布拉格衍射峰的位置的變化中得到晶格參數，從而無法得到有效的體彈模量.由此，他們提出了一種納米晶粉末衍射數據的分析方法，該方法基于單個布拉格衍射峰計算晶格常數，并稱之為“表觀晶格常數”(apparent lattice parameters，alp)，在數值上與Q=2π/d相關，其中d為hkl衍射峰對應的晶面間距，單位為?.理論計算和實驗結果都表明alp值與Q具有復雜的相關性，并具有一定的特征極小值和極大值.仔細分析這些特征就有可能揭示納米晶的晶體結構和特征，特別是表面層的結構和變形行為.根據Palosz的分析，在很大的Q值下觀測到的衍射數據可以用來研究晶核的性質(即納米晶核的真實晶格常數)，而在較小的Q值下觀測到的衍射數據則對晶粒表面(即殼層)的結構信息更加敏感.

基于alp的概念，在目前的實驗結果中根據不同的衍射峰分別計算了納米晶和微米晶Ni的單胞體積(alp)3，并用公式(1)對其進行擬合，得到與Q值相對應的體彈模量如圖3所示.對于微米晶Ni，通過不同衍射峰得到的體彈模量數值基本相同，與Q值無相關性；對于納米晶Ni，在Q= 3.1～3.5 ?-1時的體彈模量明顯低于Q= 5.0～5.9 ?-1時的數值(減小約10%).由于粉末X射線衍射實驗可獲得的Q值范圍有限，實驗得到Ni的Q值范圍較窄(≈ 3～6 ?-1)，無法準確地確定晶格常數，從而無法準確地確定晶核的壓縮性能.然而，對于具有表面殼層應變(膨脹)的納米晶廣義模型(Palosz et al.,2002;Zhang et al.,2007;Chen et al.,2008)(如圖3中的插圖所示)，我們的研究表明納米晶Ni的表面層比晶粒內部的可壓縮性更強.據此還可以推斷，與晶粒內部相比，表面殼層具有某種膨脹結構，原子間距離更長.

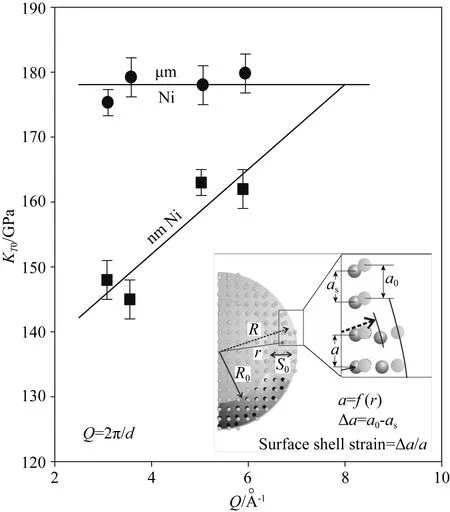
圖3 不同衍射矢量Q下納米晶和微米晶的體彈模量.體彈模量數值通過“表觀晶格常數”由單獨的布拉格衍射峰計算得出

有研究者利用分子動力學模擬研究了納米晶Ni體彈模量的晶粒尺寸依賴性(Zhao et al.，2006)，計算的P-V數據表明納米晶Ni比單晶Ni的體彈模量減小了7%，與我們的研究結果十分接近.如果將塊體納米晶的體彈模量表示為晶粒表面殼層和內部核的模量組合，利用一個簡單的混合定則模型可以得出在286 K時表面殼層的體彈模量比晶粒內核小9.2%，該結果也與我們的實驗結果一致.因此，實驗和理論計算都表明，納米晶Ni的“整體”抗壓縮性的減小是晶粒表面殼層抗壓縮性減小的結果.我們的研究表明，將粉末衍射與壓縮實驗相結合的方法是探索納米材料表面殼層結構和行為的有效手段.

2.2 納米晶Ni的表觀應變和晶粒尺寸計算方法

屈服強度(σy)是材料的一個重要性能指標，用來定義塑性變形和黏滯流動的開始階段，通常由材料的應力-應變曲線測量來確定.高強度同步輻射X射線衍射技術和飛行時間中子衍射技術則可以實現在原子尺度上對塊體樣品進行形變研究(Weidner et al.,1994a；Zhang et al.，2002；Brown et al.，2003；Qian et al.，2005).基于經典的Williamson-Hall方法及其后續演化方法(Williamson and Hall，1953；Gerward et al.，1976；Weidner et al.,1994b；Révész et al.，1996；Ungár and Borbély，1996；Ungár and Tichy，1999)，可以從衍射數據的峰寬分析中得到應變、強度、位錯密度和晶粒尺寸等信息.我們對納米晶和微米晶Ni進行了3次高壓同步輻射X射線衍射實驗和2次高溫中子衍射實驗.在所有的同步輻射X射線衍射實驗中，納米晶和微米晶Ni被裝入同一樣品腔，以便直接和準確地對比二者的性能差異.在中子衍射實驗中，將Ni粉裝入直徑為6.35 mm的釩管中，在真空條件下進行原位加熱，溫度范圍為318～1073 K，每個衍射圖譜的采集時間為2 h.圖4和圖5分別為選定壓力和溫度下的同步輻射X射線衍射和中子衍射圖譜，顯示了不同溫壓條件下峰寬的變化.

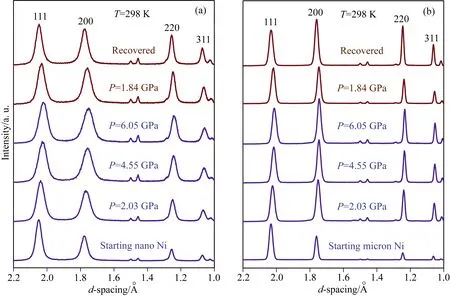
圖4 (a)納米晶和(b)微米晶Ni在298 K和選定壓力下，從單次高壓實驗得到的同步輻射X射線衍射圖譜

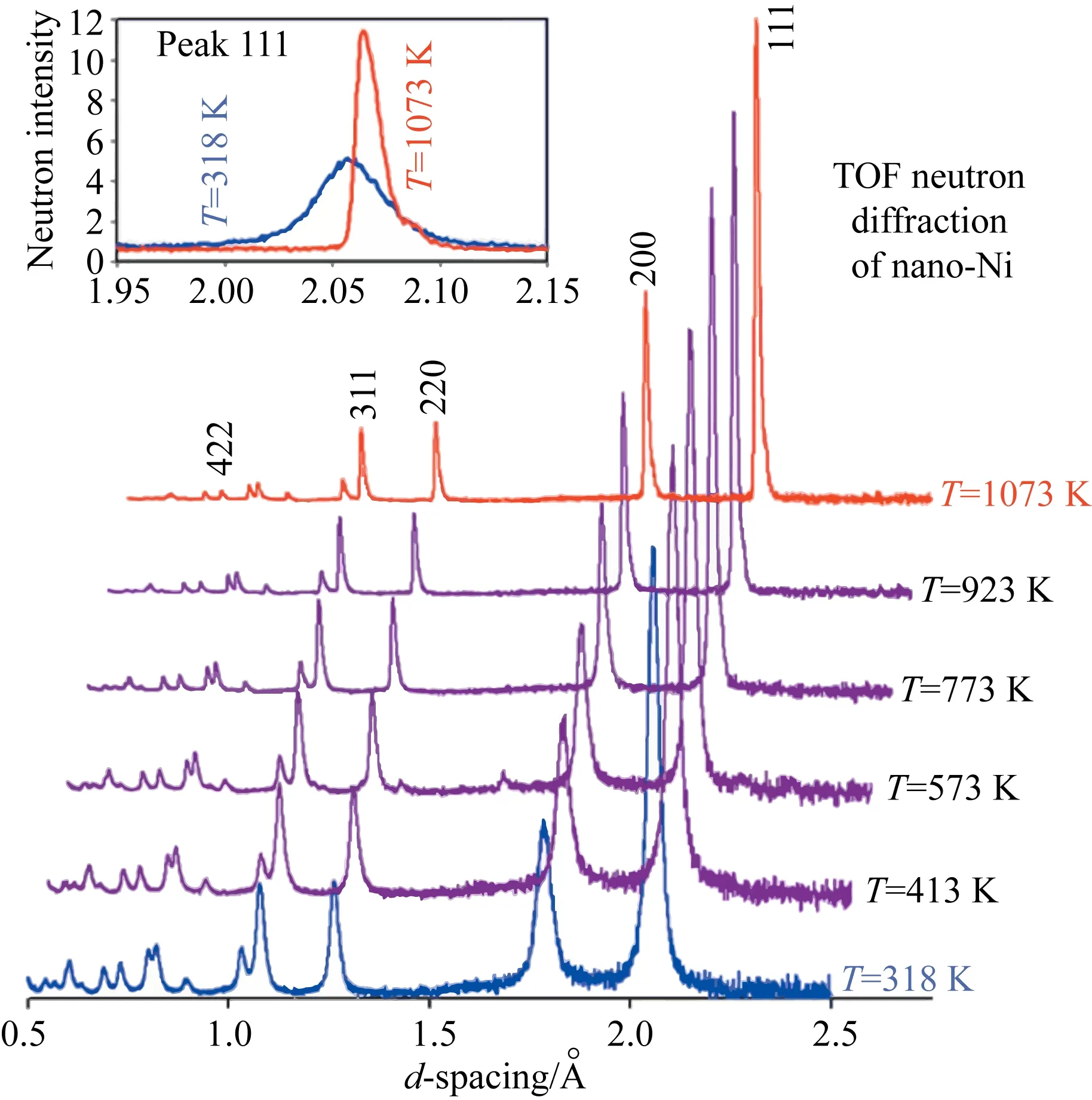
圖5 納米晶Ni在常壓和選定溫度下的飛行時間中子射線衍射圖譜

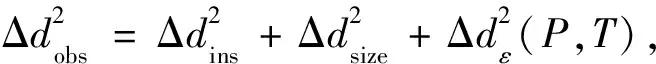
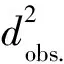
圖6所示數據表明，觀測到的原始數據(圖6中黑色空心圓圈)呈現出顯著的分散性，并且隨著壓力增加分散性增大.這種數據的分散性在微米晶Ni或其他微米尺度的陶瓷或礦物樣品中并未被發現.由于數據點分散，不能通過簡單的直線對其進行擬合進而得出應變和晶粒尺寸信息.由此，我們提出了一種基于不同晶面的楊氏模量的修正方法：

(3)

其中，S1和S2為彈性柔度數據.對于納米Ni，我們根據衍射彈性比的平方(DER2)，提出了以下歸一化路線，并選擇柔度最小(hkl=111)或最大(hkl=200)的晶面作為參考：

DER2=(Ehkl/E111)2,

(4)

以及

DER2=(Ehkl/E200)2.

(5)

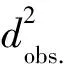
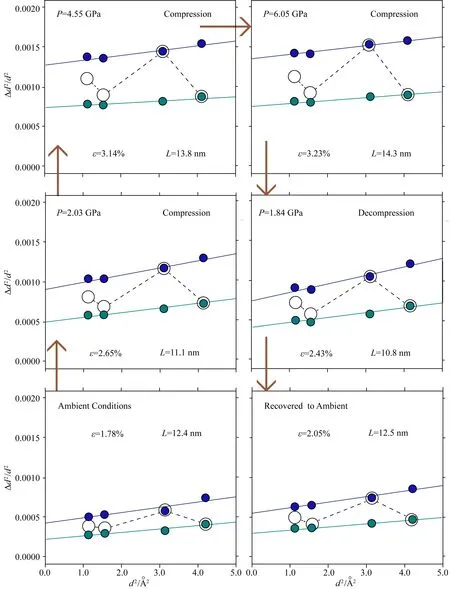
圖6 納米晶Ni中Δ/d2隨d2(P,T)的變化趨勢

2.3 納米晶Ni的屈服與升壓-卸壓能量耗散

我們通過兩組同步輻射X射線衍射實驗在室溫下同時研究了納米晶和微米晶Ni的加載和卸載循環.在兩次衍射實驗的最大壓力下(分別為1.4和6.0 GPa)，用公式(2)測定的納米晶Ni的應變絕對值比微米晶Ni高3～4倍.為了便于比較，我們將實驗得到的應變與在最高壓力下的最大應變值進行了歸一化，結果如圖7所示.從圖7中可以看出，微米晶Ni在Py1=0.4 GPa和Py2=1.6 GPa有兩個明顯的屈服點，對應的歸一化應變量分別為εnorm=0.7和εnorm=1.0.第一個屈服點代表粉末在壓縮過程中在晶粒接觸位置的高應力集中處產生的“局部”屈服；第二個屈服點表示整個樣品的“宏觀”塑性變形，也是經典力學中“屈服”的真正含義.

相比之下，在納米晶Ni中并沒有觀察到這兩個屈服點，“局部”塑性變形階段預計在遠低于0.4 GPa的壓力下發生，很難用我們目前使用的實驗技術來確定.另一方面，納米晶Ni在高應變下觀察到了明顯的加工硬化作用.根據最大壓力的不同，納米晶Ni在卸載時具有更大的應變回復率，約為83%～84%，而微米晶Ni僅為49%～52%.不可回復的應變可以由晶間(如彈性和塑性的各向異性)或晶內(如應力和位錯密度的非均勻分布)機制引起.前期的研究(Budrovic et al.，2004)表明，納米晶Ni在單軸拉伸作用下，位錯密度可完全恢復.在我們的三軸壓縮實驗中，納米晶Ni不可回復的部分源于晶粒之間(彈性和塑性的各向異性)的應變，而微米晶Ni的不可回復的部分源于晶粒內部(位錯密度)的應變.

從圖7中還可以看出，屈服后的樣品(b)比屈服前的樣品(a)具有更顯著的加載-卸載遲滯回線，但兩種樣品在屈服前后的應變恢復率相當，表明Ni的位錯密度在彈性加載階段趨于飽和，在塑性變形階段沒有進一步增加.屈服后微米晶Ni的遲滯回線很大，說明高壓對微米晶Ni的作用以熱量的形式消散.相比之下，納米晶Ni的遲滯回線很小，說明在加工硬化塑性變形階段的能量損失明顯降低.納米晶Ni在加載-卸載循環過程中能量耗散水平的降低表明，納米材料在循環加載中可以承受更大的機械疲勞，這是納米力學的一個重要發現.

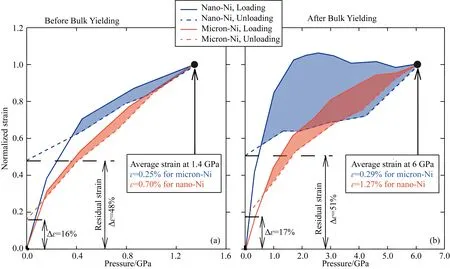
圖7 加載(實線)和卸載(虛線)過程中納米晶Ni(紅線)和微米晶Ni(藍線)的歸一化表觀應變隨壓力的變化曲線

納米晶Ni在室溫下升壓和卸壓時晶粒尺寸隨壓力的變化如圖8所示.在壓縮過程中，三個獨立的實驗顯示，在屈服壓力之前(即在～1.8 GPa以下的彈性變形階段)，樣品的晶粒尺寸減小或發生破碎.該現象在硬脆性陶瓷材料中也可以觀察到(Qian et al.，2005)，其原因為高壓會抑制原子擴散并提高樣品黏度.當P=7.4 GPa時，即納米晶Ni發生整體塑性屈服后，在室溫下觀察到了納米晶Ni的晶粒長大了約60%.對于納米晶Ni，壓縮過程中在塑性屈服/黏性流動階段的晶粒生長是由“冷焊”引起的.在較大的偏應力驅動下，晶粒間的原子擴散和晶格旋轉會使“非擇優取向”的納米晶粒相連接，從而導致晶粒長大.我們的實驗結果與Shan等(2004)的研究一致，他們認為納米晶Ni在拉伸時發生的晶粒長大是由塑性變形時晶粒的旋轉所導致.卸壓后樣品晶粒尺寸的變化與升壓過程中觀察到的趨勢相似，當壓力完全釋放后，晶粒尺寸恢復到初始值.這種可逆性晶粒尺寸變化的原因尚不清楚，但可能與卸壓過程中樣品所經歷的不同應力狀態有關.

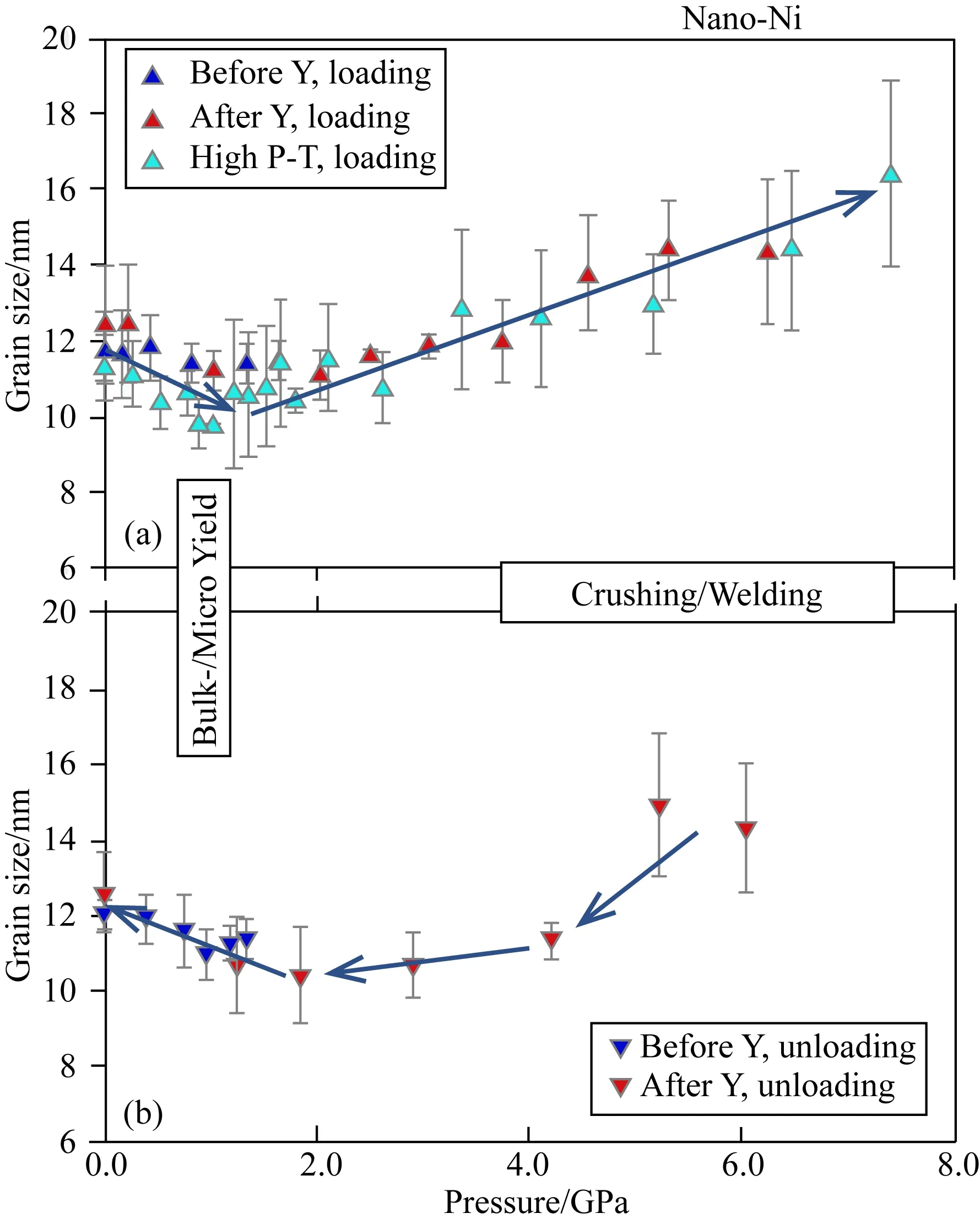
圖8 納米晶Ni在室溫下(a)加壓和(b)卸壓過程中晶粒尺寸隨壓力的變化趨勢

2.4 納米晶Ni的高溫高壓應力分析

我們使用同步輻射X射線對微米和納米晶Ni同時在高溫高壓條件下進行了對比實驗，壓力和溫度的極值分別為7.4 GPa和1400 K.為了比較微米和納米晶Ni的高溫力學性能，根據實驗結果將表觀應力表示為壓力和溫度的函數，結果如圖9所示.在計算時，首先利用衍射數據根據公式(2)計算出表觀應變，然后通過σ=E·ε計算出表觀應力.根據圖2中的結果，納米晶Ni比微米晶Ni的彈性模量減少了10%，因此在計算中納米晶Ni和微米晶Ni的楊氏模量分別取E=180 GPa和E=200 GPa.盡管該數值忽略了壓力和溫度對彈性模量的影響，但并不會對整體的變化趨勢產生影響.

納米晶和微米晶Ni的初始應力差是由殘余應力、表面應變和晶粒尺寸效應造成的.隨著壓力的增加，在彈塑性過渡區，即從“微觀/局部”屈服到“宏觀/整體”屈服階段，納米晶Ni的晶粒間的接觸應力以更大的速率增加.當整個樣品的強度小于偏應力或剪切應力時，即開始發生宏觀/整體屈服，并伴隨著塑性變形或黏性流動的開始.相應的，在發生宏觀屈服后衍射峰寬度變化不大，說明樣品中的位錯密度達到了飽和.

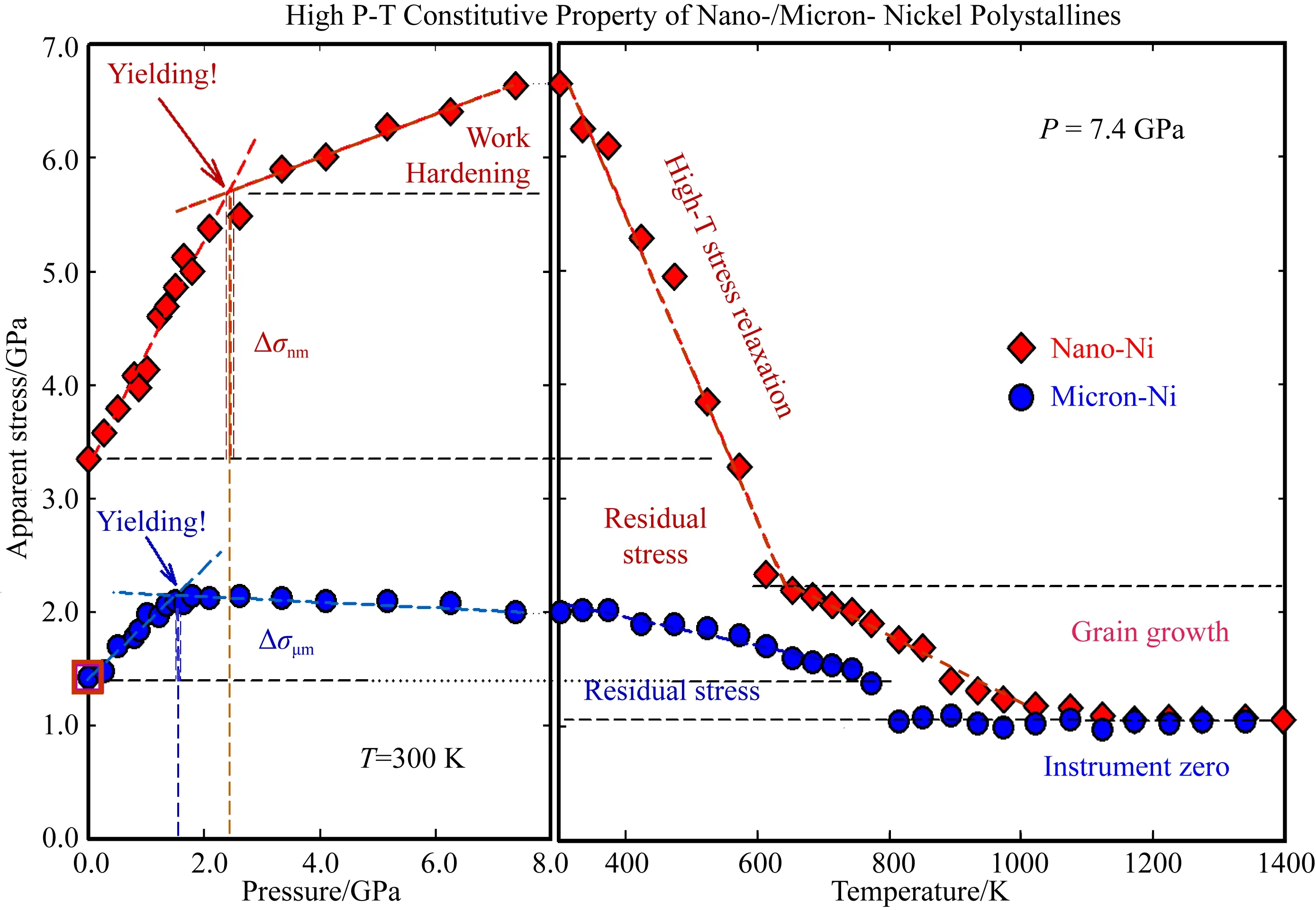
圖9 納米晶和微米晶Ni的表觀應力隨著壓力和溫度的變化曲線，其中包含了微觀應變和儀器影響.“屈服”點為彈性加載階段和塑性加工硬化/軟化階段的交點.兩種樣品顯示出了不同的初始屈服壓力

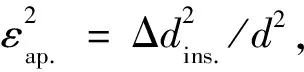
在所有實驗溫度下，用公式(2)得到的晶粒尺寸如圖10所示.當溫度小于573 K時，納米晶Ni沒有發生晶粒長大現象；在573～773 K溫度范圍內，經E200和E111修正后，晶粒尺寸分別從13.5 nm增長到36.8 nm和從18.1 nm增長到49.3 nm；溫度大于823 K時，晶粒迅速長大并接近微米尺度.圖10還給出了壓力為7.4 GPa時晶粒尺寸隨溫度的變化規律.當溫度小于573 K時，晶粒尺寸基本保持不變；當溫度繼續升高時，晶粒的長大速率與常壓相比明顯減小.這些結果表明，壓力是控制結晶過程的一個有效的熱力學參數.由于晶粒生長通常伴隨著長程原子重排，它在高壓下在動力學上將受到阻礙或抑制.因此，壓力也是合成納米結構陶瓷材料的關鍵控制參數(Zhao et al.，2004).

圖10 納米晶Ni在常壓(中子衍射數據)和7.4 GPa(X射線衍射數據)下晶粒尺寸隨溫度的變化曲線.所有數據均由公式(2)計算得出并代表納米晶Ni的平均晶粒尺寸

2.5 納米晶Ni中的位錯密度

為了得出納米晶Ni中位錯密度ρ隨退火溫度的變化規律，我們利用中子衍射數據結合以下公式進行計算(Shen et al.，1995)：

(6)

其中，b為位錯伯氏矢量的絕對值，A為常數，取值為3.3(Révész et al.，1996)，C是取決于材料的彈性各向異性的對比系數，可以通過C44/(C11-C12)和C12/C44來表征，其中C11、C12和C44為彈性常數.公式(6)中的所有其他參數與公式(2)中的含義相同.

由公式(6)得到的位錯密度和晶粒尺寸隨退火溫度的變化趨勢如圖11所示.對比圖10和圖11中可知，由公式(2)和公式(6)所得到的晶粒尺寸的絕對值以及隨溫度的變化趨勢是一致的.初始納米晶Ni的位錯密度約為0.053 nm-2，當溫度為573 K時，位錯密度約為0.019 nm-2，減小了約三分之一.當溫度在573～873 K范圍內時，隨著溫度的升高，位錯密度不斷減小，晶粒尺寸不斷增大.

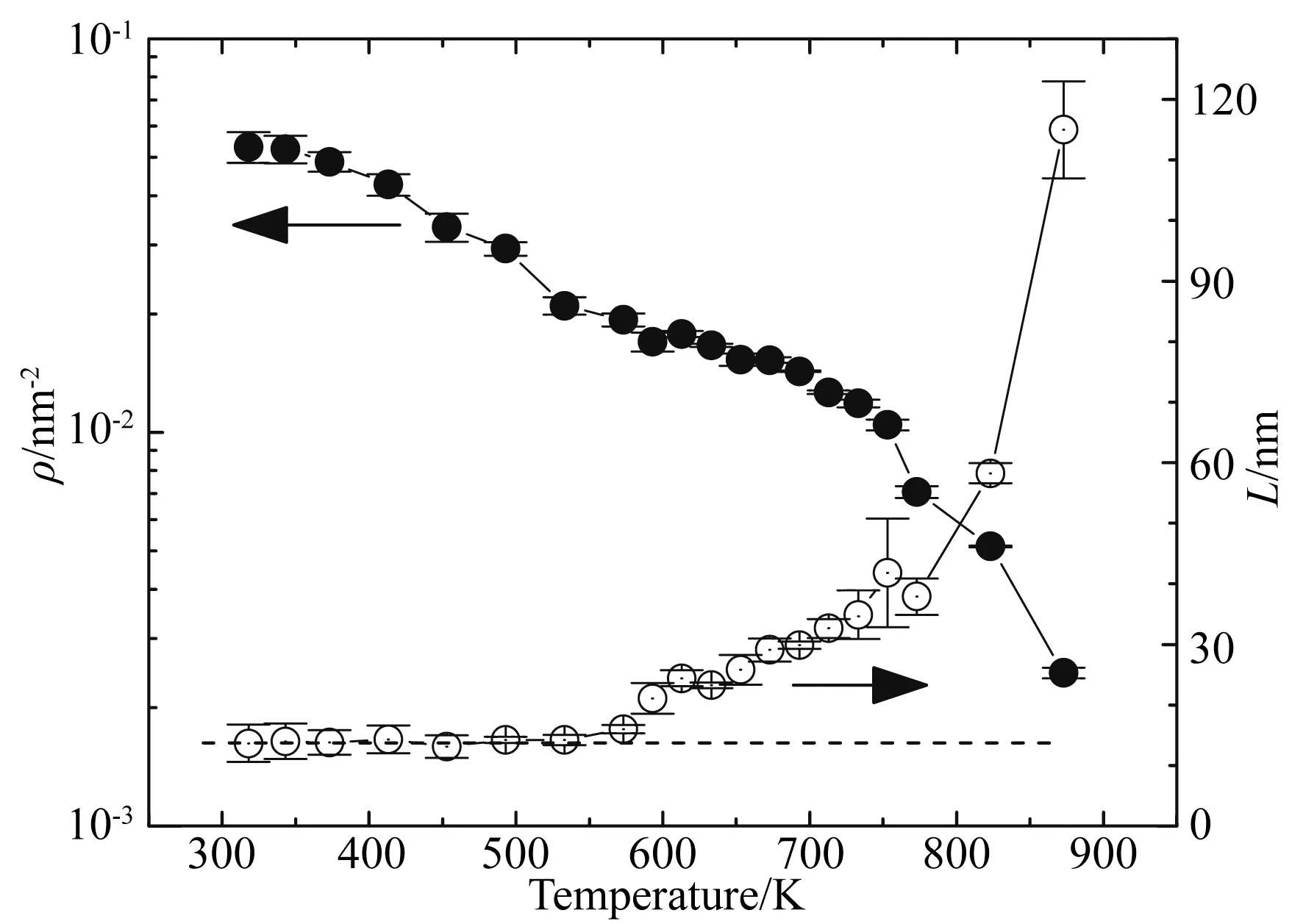
圖11 納米晶Ni的位錯密度ρ和晶粒尺寸L隨溫度的變化關系

Ashby(1970)認為，晶體在塑性變形中產生的位錯可以分為“幾何必需”位錯(與晶界的存在相關的位錯)和“統計存儲”位錯(參與塑性變形的滑移位錯).在圖11中，存在一個晶粒尺寸保持不變但位錯總密度顯著下降的溫度范圍.晶粒尺寸恒定表明在該退火溫度范圍內“幾何必需”位錯的密度沒有發生改變，而實驗觀察到的總位錯密度的下降是由于球磨過程中“統計存儲”位錯的湮滅所導致的.在較高的退火溫度下，晶粒尺寸增大是由幾何必需位錯密度減小造成的.顯然，這兩種不同類型的位錯在納米晶Ni中都與晶粒尺寸的變化有關.

3 結論

通過高溫高壓下的同步輻射X射線衍射和飛行時間中子衍射實驗，我們提出了一種利用衍射數據研究和分析納米晶本征力學性能的方法.利用該方法研究了納米晶的彈性軟化、微觀應變、屈服強度、位錯密度以及高溫下的力學性能等.結果表明，在納米晶Ni中存在明顯的彈性軟化現象，并證實了納米Ni具有張性殼層.根據衍射數據的峰形分析得到了納米晶Ni的屈服強度為2.35 GPa，是微米晶Ni的3倍以上；與單軸拉伸實驗相反，納米晶Ni在高壓塑性變形階段表現出明顯的加工硬化，而微米晶Ni則在高壓下表現出了一定的加工軟化，并有較大的能量耗散.加載-卸載循環過程中的遲滯回線表明，納米晶Ni的能量耗散比微米晶Ni顯著降低，說明納米材料在循環加載過程中能夠承受更大的機械疲勞.納米Ni在彈性變形階段表現出了晶粒破碎現象，而在高壓加載下的整體塑性變形過程中晶粒穩定生長.在高溫退火過程中，隨著溫度的升高，納米Ni在573 K以上出現了明顯的應力降低和晶粒長大現象.在高溫下，7.4 GPa下的晶粒生長速率明顯小于常壓下的晶粒生長速率，表明壓力是控制晶化過程的有效參數.對納米Ni中的位錯密度進行計算的結果表明，晶粒尺寸隨溫度和壓力的變化與“幾何必需”位錯和“統計存儲”位錯都具有相關性.本文使用的方法可以定量測定巖石礦物的高溫高壓流變強度，為反映大陸中上地殼的真實流變結構情況及發生在中上地殼的地震及其余震深度分布規律探索提供新的研究方法，為研究巖石圈以及地幔物質的蠕變對流提供了高科技的研究手段.