行星引潮力與太陽活動關系新探

王建，王琳琳，孫威，王婕

1 南京師范大學地理科學學院，南京 210023 2 江蘇第二師范學院城市與資源環境學院，南京 211200 3 江蘇省地理信息資源開發與利用協同創新中心，南京 210023 4 上海工程技術大學數理與統計學院，上海 201620

0 引言

太陽活動不僅與地球氣候密切相關(趙新華等，2014；趙平和周秀驥，2011；Hampson et al.，2005)，而且還會影響地球自轉的周期(廖德春和廖新浩，2001)，因此太陽活動的形成機制一直備受關注.關于太陽活動的成因，目前主要有兩種理論，一種是太陽內部的磁流發電機理論，另一種是太陽外部的行星運動理論(聶清香等，2007；劉復剛和王建，2013a，2014).在行星引力理論中，討論比較多的是行星引潮力與太陽活動之間的關系.

關于行星引潮力與太陽活動的關系，長期以來一直是科學家討論的重要問題，甚至一度成為一個激烈爭論的熱門問題(聶清香等，2007；劉復剛和王建，2013a).Takahashi(1968)計算水星、金星、地球、火星、木星、土星對太陽的引潮力，將1928—1971間44年的引潮力與太陽黑子數年均值進行對比，發現兩者相關程度較高，但有2年的時間差.Wood(1972)考慮金星、地球與木星的位置關系，利用引潮力公式計算這三個行星在太陽上引起的潮汐高度，將其絕對值曲線與太陽黑子數進行對比，基本上峰值、谷值一一對應，有一些地方太陽黑子滯后1—3年.Condon和Schmidt(1975)研究發現行星引潮力高度只有0.1～1.0 mm級，也沒有明顯的時間對應，不贊成行星引潮力是太陽黑子起源的原因.Dingle等(1973)，測算了太陽第19周期1000個耀斑的經度位置，與木星和金星的軌道經度位置比較，結果顯示沒有潮汐影響的證據.陳協珍(1993)對歷史上發生的22個特大耀斑活動區域進行行星攝動力的計算分析，發現其中16個發生在行星對日面耀斑活動區域的攝動力比較大的時候，太陽活動受行星攝動力的調制.董士侖(1996)對于較大的太陽耀斑的發生時間和空間位置與行星位置關系的研究卻發現，引潮力觸發耀斑的各種假設都分別優于耀斑隨機發生的假設.Okal和Anderson(1975)計算木星、金星、地球、水星對太陽某點引潮力的累加，計算出來的引潮力只有11.9年周期，而太陽黑子中的9.8年、8.3年、95.8年周期并不存在于行星引潮力周期中，因此不贊成引潮力是太陽活動的重要驅動力.De Jager和Versteegh(2005)比較了太陽內部強剪切層的三種加速度：行星潮汐力引起的加速度、太陽繞轉加速度以及觀測到的加速度，發現觀測到的加速度是前兩者的1000多倍，由此認為行星作用太小，不能顯著地影響太陽活動.Hung(2007)計算金星、地球、木星180年行星直列指數值的前25%水平分布在每3.64年的天數，與太陽黑子數每年的數量進行對比，發現兩者基本對應，認為行星引起的潮汐的會聚和擴散可能提供一個壓力差，改變日冕磁場中的等離子體運動，導致其在太陽大氣磁場中移動重塑、合并擴散，從而導致太陽活動增加.聶清香等(2007)利用N體積分算法全面系統的計算了過去300年行星對于太陽引潮力的合力變化，發現引潮力合力的變化有明顯的約 11年周期和60年周期，與黑子數的周期一致，認為盡管行星引潮力偏小，但是如果與太陽內部磁流體同頻共振則有可能對太陽活動做出合理的解釋.Seker(2013)模擬計算了太陽黑子出現地點與四顆起潮行星水星、金星、地球和木星所處位置之間的關系，發現兩者之間關系不密切.但是他認為由于太陽黑子可能產生于光球下，因此也不確定太陽黑子就是與行星引潮力無關.劉復剛等(2013a)計算分析發現，引潮力造成的太陽表面物質加速度變化只有太陽自轉變化造成的太陽表面物質加速度變化的兩萬分之一，因此認為造成太陽11年黑子活動周期和22年磁周期形成的主要原因，不是引潮力的變化，而是太陽自轉速度的變化.

綜上所述，有的以周期的吻合性或者變化時間、空間的一致性認為行星引潮力與太陽活動密切相關；有的則以行星引潮力的量級太小，以及周期和時間空間位相的不一致性否定它是太陽活動的主要起因.然而，有個問題似乎被忽視了，就是如何計算行星對于太陽的引潮力尤其是引潮力的合力.實際上，不同的計算方法得出的引潮力的大小、周期是不同的，甚至相差很大.本文擬從引潮力的計算方法著手來重新梳理不同的計算方法所得出的結果的異同，進而討論行星引潮力與太陽活動之間的關系，以期為行星引潮力與太陽活動關系的探討提供新的思路.

1 行星引潮力計算方法

關于行星引潮力的計算，早期往往局限于對于單個行星引潮力或者少數幾個行星引潮力合力的計算(劉復剛和王建，2013a，2014；Wood，1972)；探討與太陽活動的關系，往往是利用行星公轉和會合周期與黑子周期之間的對比而進行的(Dingle et al.，1973).后來隨著科學技術的進步，出現了越來越全面系統的計算方法.聶清香等(2007)利用N體積分算法全面系統的計算了過去300年行星對于太陽引潮力合力的變化序列，劉復剛和王建(2013a)利用行星會合指數運動學方程重建了過去500年行星對于太陽引潮力合力的變化序列.但是一般來說，都是利用引力差計算法，就是利用行星對于太陽中心(質心)與太陽表面之間的引力差來計算行星對于太陽的引潮力.這種計算方法，容易導致對于正垂點和反垂點同時漲落潮現象的理解出現困難，畢竟引力的方向可能與反垂點漲潮的方向不一致.還有一種計算方法是引力與繞轉慣性離心力之差計算法，就是通過太陽表面某點所受到的行星引力與太陽繞公共質心旋轉所產生的慣性離心力之差來計算行星對于太陽表面某點的引潮力.這種算法對于理解正垂點和反垂點漲落潮方向比較容易，但是要計算太陽分別與八大行星的繞轉慣性離心力比較困難.

由于涉及到八大行星，要計算八大行星對于太陽引潮力的合力，在上面兩種基本方法中又可能劃分出多種不同的合力計算方法.比如引力差計算方法，又可進一步分為引力差的矢量和計算法、引力矢量和之差計算法(圖1).計算引力差的矢量和或者引力矢量和，也有像“N體積分算法”(聶清香等，2007)和“會合指數運動學方程法”(劉復剛和王建，2013a)等不同的算法.

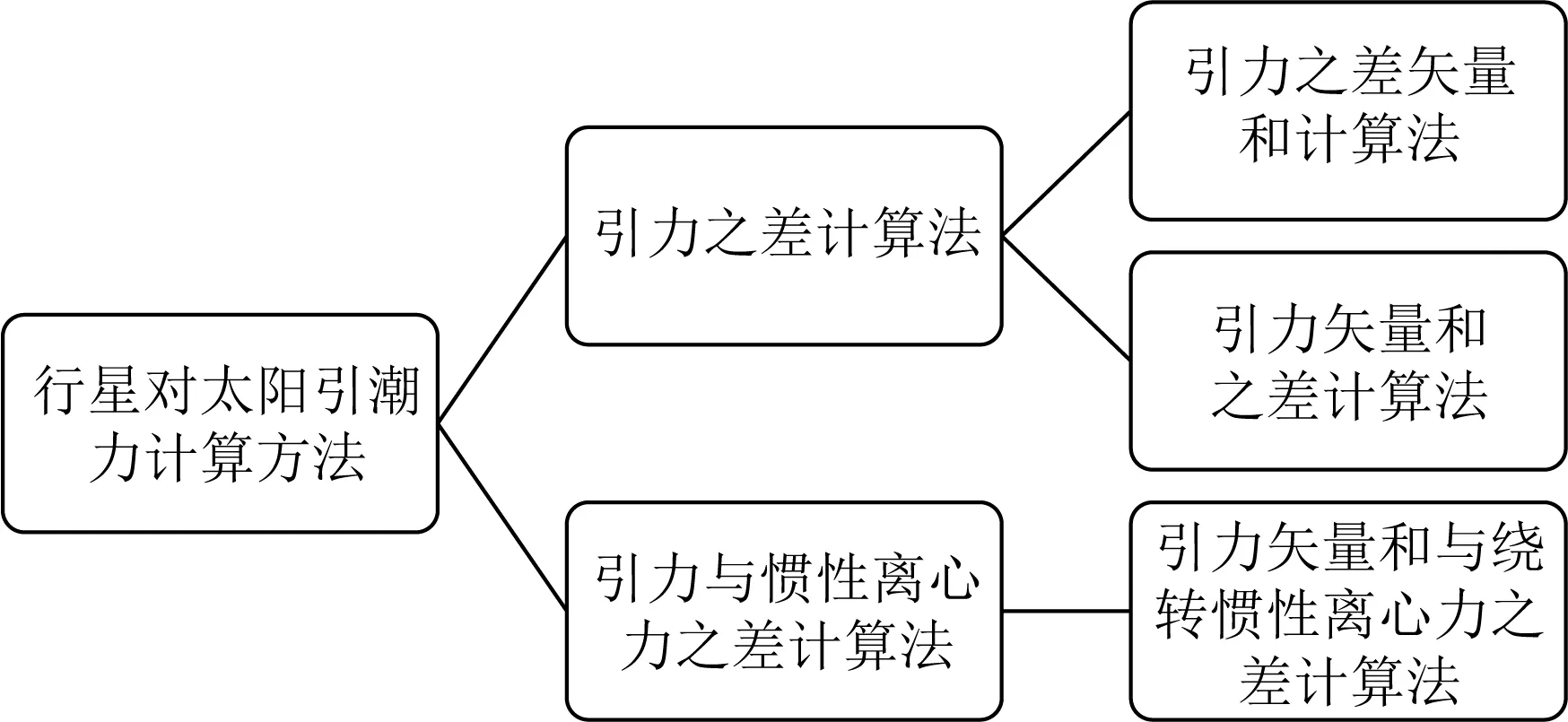
圖1 行星對太陽引潮力合力的計算方法

2 不同方法計算結果的比較

2.1 引力矢量和之差計算法及其結果

根據萬有引力公式可以計算每顆行星對于太陽中心(質心)和太陽表面任意一點引力的大小.如果以地球對于太陽中心(質心)的引力為1，其他行星對于太陽的引力的相對數可以作為引力半徑(表1).將引力半徑代入劉復剛和王建(2013b)建立的行星會合指數運動學方程：

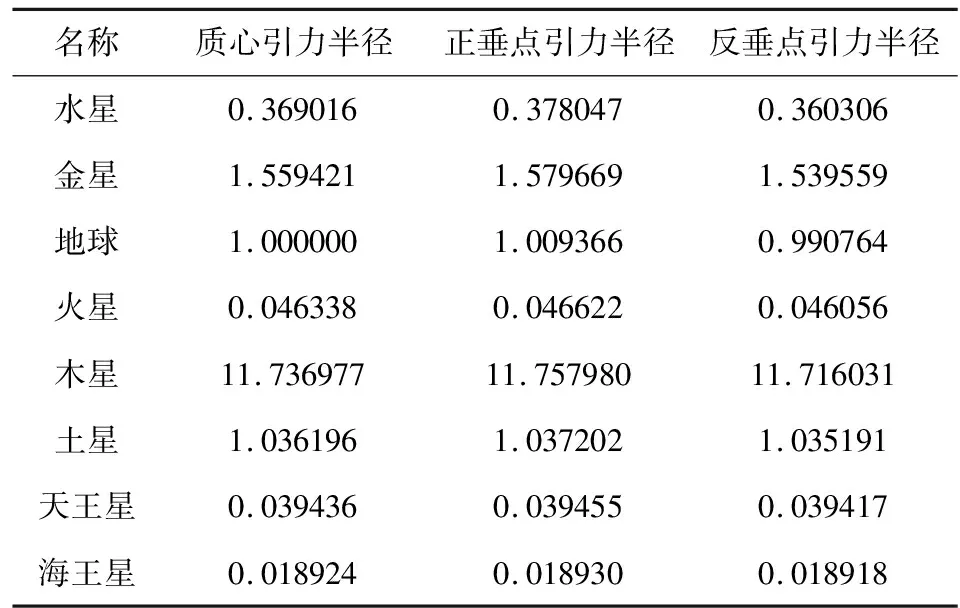
表1 八大行星引力半徑

(1)

其中，K，ri，φi，ωi，t分別為行星會合指數，各行星質量權重半徑，行星初始日心經度和平均角速度和時間.以各行星的引力半徑替代質量權重半徑，就可以分別計算出八大行星對于太陽質心、正垂點、反垂點的引力矢量和.正垂點、反垂點與太陽質心之間的引力矢量和之差就是它們的引潮力合力(圖2).

從圖2不難看出，正垂點和反垂點的引潮力大小、波動周期和相位基本一致.最顯著的周期約為12.5a和2.2a.

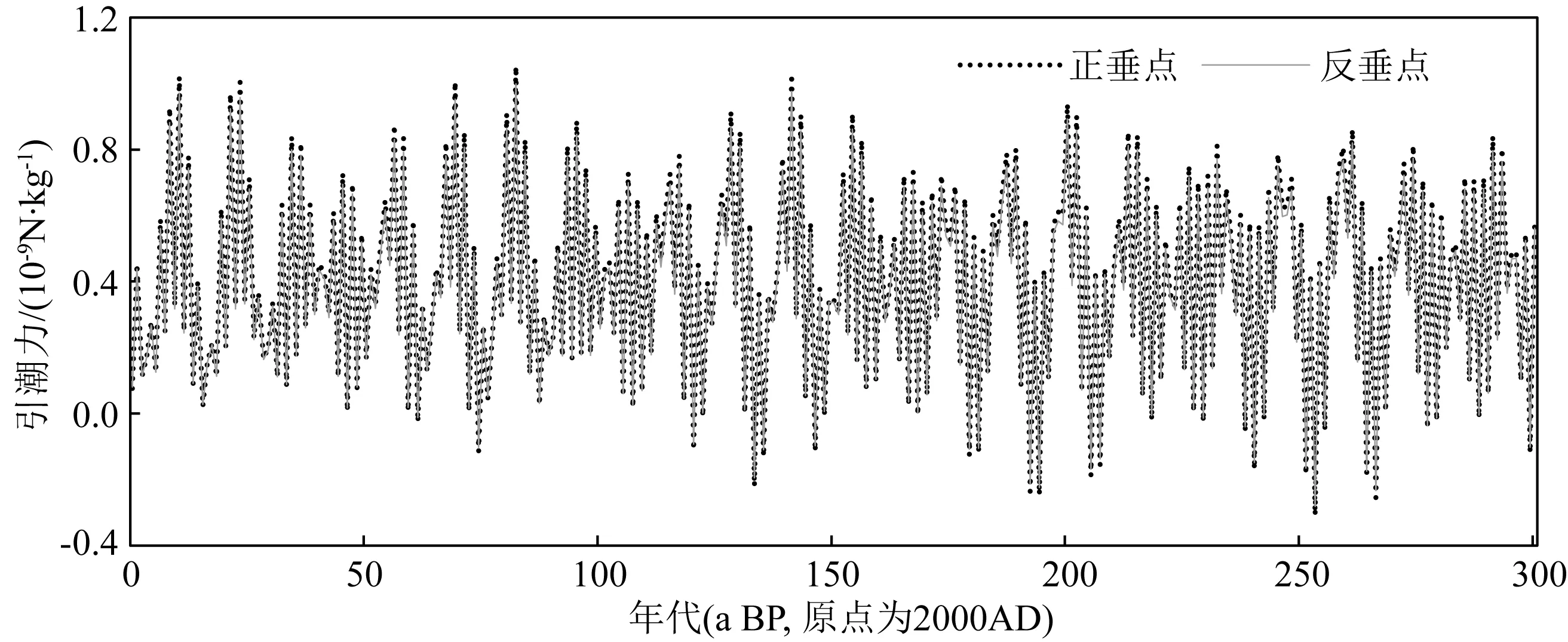
圖2 引力矢量和之差計算法計算的太陽表面赤道附近正垂點(點線)和反垂點(實線)的行星引潮力合力

2.2 引力之差矢量和計算法及其結果

這是最常用的一種方法，就是根據太陽表面一點與太陽中心引力之差來計算各個行星對于太陽的引潮力.

以正垂點為例，引潮力為

(2)

其中，G為萬有引力常數，M為行星質量，R為太陽半徑，D為行星距太陽質心的距離，Δm為太陽表面正垂點物質的質量.

根據公式(2)可以計算出各個行星對于太陽表面正垂點單位質量的引潮力，如果以八大行星對于太陽表面赤道正垂點的引潮力總和為1，那么各個行星引潮力所占比重就是行星引潮力的權重(表2).

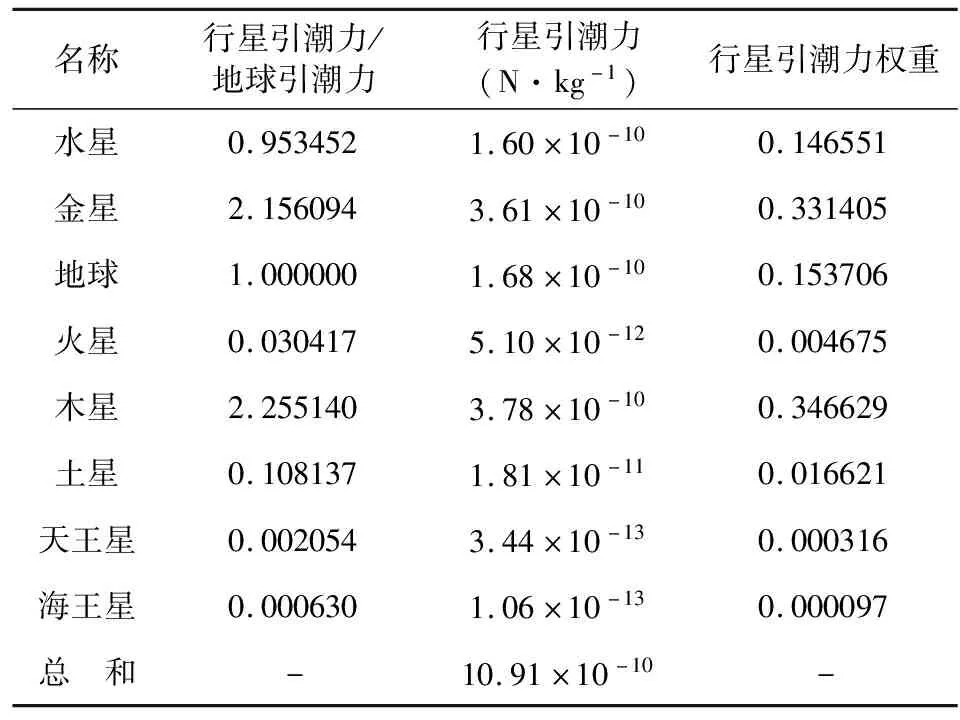
表2 各行星對于太陽赤道正垂點的引潮力大小及其權重

如果將各個行星的引潮力權重代入公式(1)，替代原來的質量權重半徑，就可以計算出八大行星對于太陽表面赤道正垂點的引潮力矢量和(圖3a).不難看出，過去300年的引潮力變化特征與方法1計算結果比較相似.

大家知道，潮汐往往是對稱分布的.比如，地球上的潮汐主要受到月球引潮力和太陽引潮力的影響和控制，當月球、太陽與地球在一條直線上時，無論月球和太陽是否在地球的同一側，地球的正垂點和反垂點均發生大潮.也就是說，即使月球和太陽分列地球兩側，它們的引潮力也是疊加的.但是，過去在計算八大行星引潮力矢量和時，沒有注意到這個問題.為了解決這個問題，應對方程(1)進行了修改.假定正垂點和反垂點位于X軸上，則應對X取絕對值，公式(1)就轉換成了公式(3).

K=

(3)

由此根據方程(3)可以計算太陽表面赤道正垂點八大行星引潮力的矢量和及其變化(圖3b).

從圖3不難看出，兩個序列有相似性，但也有較大差異.根據頻譜分析的結果(圖4)，圖3a序列的周期以12.0a和2.2a的最顯著，而圖3b序列的周期較多，除了12.0a和2.2a的周期外，還存在5.9a、4a、3.5a、2.7a等周期，其中5.9a等公轉或者會合半周期更加顯著.

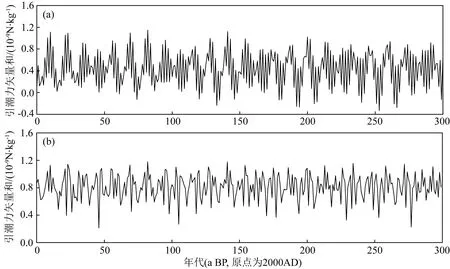
圖3 引力之差(引潮力)矢量和計算法計算的太陽表面赤道正垂點引潮力合力

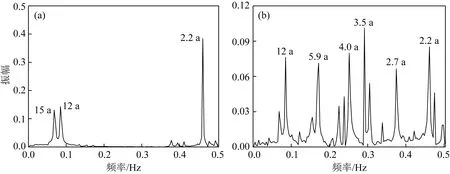
圖4 兩個序列的周期分析

2.3 引力與慣性離心力之差計算法及其結果

從引潮力的原始定義來說，引潮力就是引力與慣性離心力之差.對于地球來說，慣性離心力的大小與太陽、月球對于地心的引力相等，因此為了簡便起見，往往都是利用地表與地心的引力差來計算引潮力.

太陽的繞轉慣性離心力計算起來比較困難，因為太陽不可能同時與八大行星相互繞轉，因此也很少見到利用慣性離心力計算行星對于太陽的引潮力的例子.本文利用方程(1)計算了行星系統質心距離太陽質心的距離即行星會合指數(劉復剛和王建，2013b)，根據太陽質心與行星系統質心共同圍繞太陽系質心旋轉的特征以及關于質心的求算公式，可以計算出太陽距離太陽系質心的距離及其變化序列(劉復剛和王建，2013b；孫威等，2017).太陽距離太陽系質心的距離就是太陽圍繞太陽系質心繞轉的半徑，將繞轉半徑代入公式(4)就可以計算太陽繞轉慣性離心力.

(4)

其中，ω與v分別為繞轉角速度和線速度，r和T分別為繞轉半徑和周期.根據孫威等(2017)對于太陽繞太陽系質心變化軌跡的計算模擬發現，太陽繞轉的最顯著周期為11.865a.把r和T代入公式(4)，就可以計算分析太陽繞轉慣性離心力.由于太陽繞太陽系質心旋轉為平動，太陽各處的繞轉慣性離心力大小相等、方向相同(趙進平，2016；喬萬利，1999).正垂點的引力矢量和減去繞轉慣性離心力，就可以得到正垂點的引潮力；繞轉慣性離心力減去反垂點的引力矢量和，就可得到反垂點的引潮力(圖5).

從圖5不難看出，與前面計算出的引潮力存在顯著差異.一是正垂點與反垂點的引潮力變化是反相位的，而其他計算的引潮力是同相位的；二是這里計算出的單位質量引潮力達到10-7N·kg-1量級，比傳統計算方法計算出的引潮力(10-10～10-9N·kg-1量級)大2～3個數量級；三是其變化周期也有明顯差異.

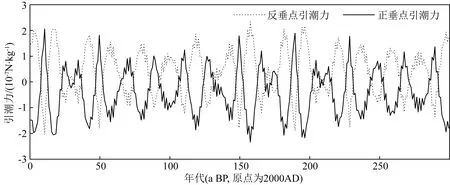
圖5 引力與慣性離心力之差法計算的太陽表面赤道正垂點(點線)和反垂點(實線)的引潮力

3 引潮力與太陽活動的關系

3.1 關于引潮力的大小

Condon等(1975)研究發現行星引潮力在太陽表面形成的潮汐高度只有0.1～1.0 mm級別.De Jager和Versteegh(2005)通過比較太陽內部強剪切層的三種加速度，發現觀測到的加速度比行星潮汐力等引起的加速度大幾個數量級，劉復剛和王建(2013a)計算分析發現，行星引潮力造成的太陽表面物質加速度變化只有太陽自轉變化造成的太陽表面物質加速度變化的兩萬分之一，因此認為行星引潮力作用太小，不是影響太陽活動的顯著動力.我們的計算發現，按照傳統計算方法計算出的八大行星引潮力合力的最大值也只有1.09×10-9N·kg-1，與太陽、月球對于地球正垂點的平均引潮力相差三個數量級，并且由于太陽上的重力加速度比地球上大幾十倍，引起的潮汐幅度確實很小.但是如果按照引力與慣性離心力之差計算的太陽上的引潮力卻可以達到2.33×10-7N·kg-1量級，比傳統引潮力大兩個數量級.從這個角度來看，我們需要對行星引潮力對于太陽活動的影響大小給予重新的分析和評估.

3.2 關于引潮力的特征

利用引力與慣性離心力之差計算出來的引潮力，不僅在量值上比傳統意義上的引潮力大得多，而且其變化特征也不相同.這個引潮力，與傳統的引潮力引起正垂點和反垂點潮汐的同相位漲落不同，該引潮力導致正垂點與反垂點潮汐的交替漲落.這種變化形式可能導致潮汐變化的幅度增大一倍.這個認識對于深入理解行星引潮力對于太陽活動的影響提供了新的依據和思路.

3.3 引潮力與太陽活動的可能聯系

如圖6所示，引潮力正值代表其方向垂直太陽表面并指離太陽，負值代表其方向垂直太陽表面指向太陽中心或者說指向太陽的背面.當引潮力為正值時，對應于該點的漲潮和背面對應點的落潮；當引潮力為負值時，對應于該點的落潮和背面相應點的漲潮.

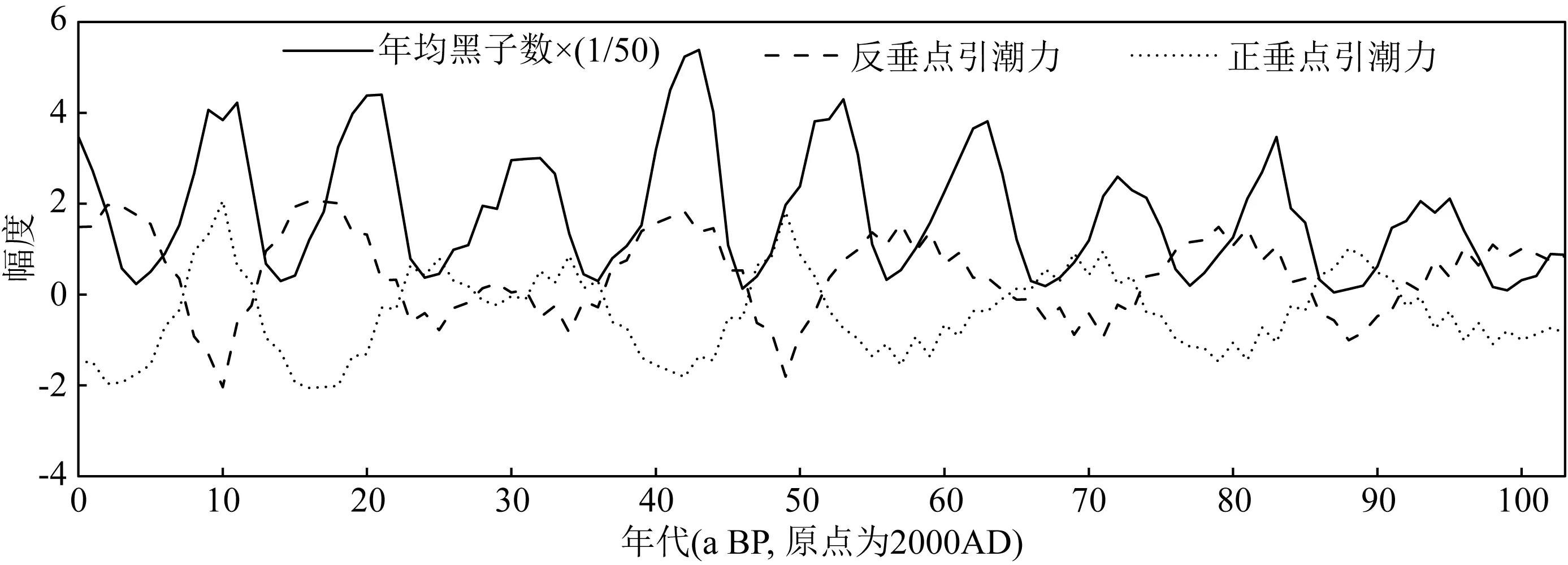
圖6 太陽表面赤道正垂點(點線)和反垂點(虛線)引潮力變化及其與太陽黑子變化(實線)的比較

太陽黑子的記錄現在已有三百多年，但是越是近期的記錄越準確可靠，該文選取了最近100年的記錄進行了對比.比較太陽赤道表面正垂點和反垂點引潮力與太陽黑子的關系(圖6)不難發現，單純利用一個點的引潮力變化很難與太陽黑子變化一一對應，利用兩點的變化組合解釋起來似乎更容易一些.總體上有這樣三個特征，一是引潮力較大時段如66～38(1934—1962 AD)、23～0(1977—2000 AD)對應于黑子峰值較大的時段，引潮力較小的時段如100～87(1900—1913 AD)、76～66(1924—1934 AD)和38～23(1962—1977 AD)對應于黑子峰值較小的時段；二是有的黑子峰值對應于正垂點的引潮力峰值、有的對應于反垂點的引潮力峰值，有的則對應于正、反垂點引潮力峰值之間；三是即使黑子峰值與引潮力峰值對應，兩者之間也大多存在相位差.這些表明引潮力與太陽活動之間存在著一定的關系，但是并不是完全一一對應的關系.說明引潮力不是太陽活動的唯一驅動因素，可能只是驅動或者觸發因素之一.太陽活動對于引潮力的響應也可能存在著時間上的滯后.

唐潔和劉曉琴(2018)研究認為，太陽黑子的飽和關聯維數為2.536，表明至少需要三個以上的變量才能有效描述太陽黑子相對數的動力學特征.因此我們可以從引潮力與太陽繞轉慣性離心力組合的角度來討論太陽黑子形成的可能原因.從圖7可以看出，從太陽繞轉慣性離心力與引潮力共同來解釋太陽黑子形成的原因，相對于用任何一個因子單獨來解釋更加有說服力.總體上來說，繞轉慣性離心力決定了黑子發生的條件和背景：峰值較大的時期往往對應于黑子峰值較大的時期，如66～38(1934—1962 AD)、23～0(1977—2000 AD)；峰值較小的時期往往對應于黑子峰值較小的時期，如100～87(1900—1913 AD)、76～66(1924—1934 AD)和38～23(1962—1977 AD).引潮力(引力之差計算出來的引潮力)在繞轉離心力的大背景下具有激發或者觸發的作用：往往引潮力的峰值對應于黑子的峰值或者此后發生的峰值.往往在慣性離心力和引潮力均處于較大值或者增大期的時候會引發較大的黑子峰值發生，如49～43(1951—1957 AD)、25～19(1975—1981 AD)期間兩個最大的黑子峰值均是如此.

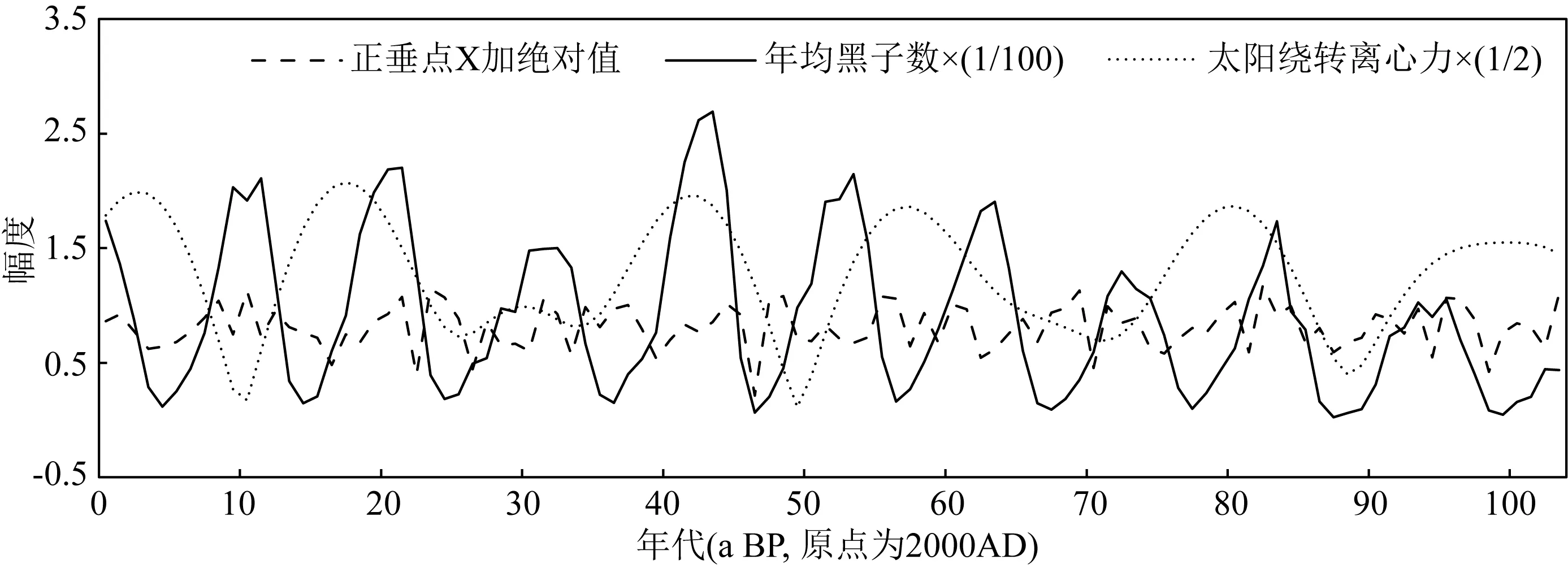
圖7 引潮力(虛線)、繞轉離心力(點線)與太陽黑子變化(實線)的比較

4 討論和結論

(1)計算方法不同，得出的引潮力變化序列可能不同.傳統的引潮力計算方法只能顯示出行星公轉周期或者會合周期，卻往往忽視了對應于行星公轉和會合半周期的引潮力變化.

(2)利用引力與太陽繞轉慣性離心力之差計算出來的引潮力，比傳統的引潮力大兩個數量，并且其變化特征與傳統的引潮力引起正垂點和反垂點潮汐的同相位漲落不同，它導致正垂點與反垂點潮汐的反相位交替漲落.

(3)太陽活動可能是多個因子共同作用的結果，單純利用引潮力一個因子難以全面系統地解釋太陽活動的特征.利用繞轉慣性離心力和引潮力共同解釋太陽活動變化特征，比傳統引潮力單一因子的解釋更有說服力.表明太陽活動是多因子共同作用的結果，行星引潮力和太陽繞轉慣性離心力可能都是太陽活動的作用因子.