基于混沌精英黏菌算法的無刷直流電機轉速控制

肖亞寧， 孫 雪， 李三平， 姚金言

(東北林業大學機電工程學院， 哈爾濱 150040)

無刷直流電機(brushless direct current motor, BLDCM)由于結構簡單、可靠性高且機械性能良好，而被廣泛應用于航空航天、國防軍事、機器人等領域[1-2]。在BLDCM轉速控制中最常用的方法是傳統比例-積分-微分(proportional integral differential，PID)控制[3]，但BLDCM是一種非線性、強耦合的復雜系統[4]，傳統PID控制品質對比例、積分和微分3個控制參數依賴性強，很難適應不同的工作條件，因此控制時往往會出現轉速調節精度不高、響應速度慢、抗干擾能力差等問題，無法達到理想的控制效果[5]。

近年來，隨著人工智能和計算機科學的蓬勃興盛，出現了大量基于自然現象啟發的群智能優化算法，例如：蜻蜓算法(dragonfly algorithm, DA)[6]、灰狼優化算法(grey wolf optimizer, GWO)[7]、鯨魚優化算法(whale optimization algorithm, WOA)[8]、饑餓游戲搜索算法(hunger games search, HGS)[9]等。這些智能算法原理簡單、易于實現，能夠有效解決各種復雜問題，因此越來越多學者嘗試利用其對BLDCM轉速PID控制器進行優化設計，以進一步控制精度和工作穩定性。文獻[10]提出了一種利用粒子群算法在線自整定PID控制方法，使得無刷直流電機具有更好的動態響應性能，但因算法本身搜索能力不足而在迭代后期易于陷入局部最優；文獻[11]采用改進遺傳算法優化無刷直流電機模糊PID控制器，可以降低穩態誤差，提高響應速度，但因遺傳算法復雜的選擇，交叉，變異過程導致參數整定效率低下，轉速控制精度有待提高；文獻[12]提出了一種基于飛蛾火焰優化算法的模糊控制器設計方法，但因算法參數較多，且根據經驗選取的模糊規則、隸屬度函數具有很大程度上的主觀性，難以達到理想的控制性能。

黏菌算法(slime mould algorithm, SMA)是一種全新的群智能仿生算法[13]，相比其他算法具有更加優秀的搜索性能，已在不同領域得到一定程度的應用。Nguyen等[14]利用SMA算法優化梯級水電站設計；Zubaidi等[15]提出了一種SMA算法混合人工神經網絡模型用于城市用水需求量的預測；Kumar等[16]成功利用SMA算法對太陽能光伏電池模型進行參數辨識。然而標準SMA算法依然面臨著初始種群質量低，探索和開發過程難以平衡，迭代后期易于陷入局部最優等問題的困擾，收斂速度和求解精度仍有很大的提升空間。

因此，為彌補傳統控制方法在BLDCM轉速調節中的局限性，進一步增強標準SMA算法的全局搜索能力，提出了一種整合Tent混沌映射和精英反向學習策略的改進黏菌算法，并將其用于優化BLDCM速度環PID控制器，實現參數在線自整定。仿真和實驗結果表明基于改進黏菌算法優化后的BLDCM轉速控制系統具有響應速度快，抗干擾能力強，搜索效率高等優點。

1 BLDCM數學模型

無刷直流電機采用三相星形連接，其等效電路如圖1所示。

圖1 無刷直流電機等效電路Fig.1 Equivalent circuit of BLDCM

無刷直流電機由定子和轉子組成，通過控制其定子繞組上的電流頻率及波形，可以改變轉子的運行狀態。為了方便分析，假定電機定子繞組完全對稱，空間上互差120°電角度，忽略磁路飽和，不計渦流和磁滯損耗，不考慮齒槽效應，電樞繞組均勻連續分布在定子內表面，得到無刷直流電機的三相定子電壓平衡方程為[17]

(1)

式(1)中：Ua、Ub、Uc分別為三相繞組相電壓；R為三相繞組相電阻；ia、ib、ic分別為三相相電流；L為定子相繞組自感；M為定子相繞組互感；d/dt為微分算子；ea、eb、ec分別為三相反電動勢。

電機運行時，任意時刻的電磁功率P為三相繞組電磁功率之和，故電機的電磁轉矩方程為

P=eaia+ebib+ecic

(2)

(3)

式(3)中：Te為電機電磁轉矩；ω為旋轉角速度。

無刷直流電機的運動方程為

(4)

式(4)中：TL為負載轉矩；B為阻尼系數；J為電機轉動慣量。

2 標準黏菌算法

SMA是由Li等[13]于2020年提出的一種新型元啟發算法，其主要模擬了自然界中黏菌覓食過程中的行為和形態變化。與其他智能優化算法相比，黏菌算法具有原理簡單、調節參數少、尋優能力強、便于實現等優點。黏菌是一種生活在潮濕寒冷環境中的真核生物，其營養的攝取主要來源于外界有機物。當黏菌接近食物源時，生物振蕩器將通過靜脈產生一個傳播波，以增加細胞質流量。食物濃度越高，生物振蕩器產生的傳播波也就越強，則細胞質流動越快，通過數學模型模擬上述逼近行為。

(5)

p=tanh|S(i)-DF|

(6)

參數a的計算公式為

(7)

式(7)中：t為當前迭代次數；tmax為最大迭代次數。

黏菌的質量系數W模擬了黏菌在不同食物濃度下的振蕩頻率，這有助于黏菌在找到高質量食物時能夠更快地接近食物，從而提高搜索效率，其表達式為

(8)

Index=sort(S)

(9)

式中：bF和wF分別為當前迭代過程中獲得的最優、最差適應度；Index為適應度序列；r為區間[0,1]上的隨機值，用于模擬黏菌靜脈收縮模式的不確定性；condition表示S(i)排序中前1/2的種群。

3 混沌精英黏菌算法

3.1 混沌初始化

研究表明，初始種群的多樣性有助于提高算法的收斂速度和準確性，SMA算法通常采用隨機數法初始化種群，在解決復雜優化問題時，存在后期種群多樣性降低，易于陷入局部最優等缺陷[18]。目前文獻中大多運用Logistic混沌映射優化智能算法產生混沌序列，豐富種群多樣性。但相較于Logistic混沌映射，Tent混沌映射更加結構簡單，收斂速度快，具有更好的遍歷均勻性。設置種群規模為500，分別采用兩種方法在區間[0,1]范圍內產生混沌序列，其空間分布直方圖如圖2所示。可以看出，Logistic混沌映射生成的序列在區間[0,0.1]和[0.9,1]范圍內的概率要高于其他各段，而Tent混沌序列在可行域內分布相對均勻。因此采用Tent混沌映射在SMA算法迭代初期進行種群初始化，使得個體位置均勻分布在搜索空間內，有助于提高算法求解效率。Tent混沌映射的數學表達式為

圖2 Logistic與Tent混沌映射分布對比Fig.2 Comparison of Logistic and Tent chaotic mapping distribution

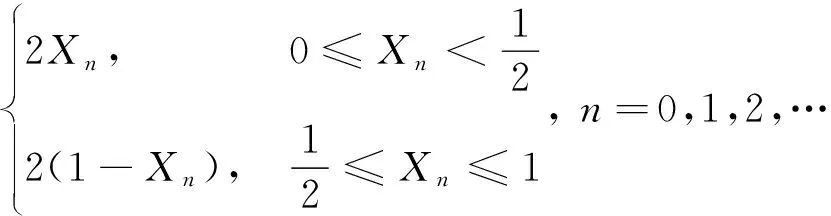
(10)

式(10)中：n表示映射次數；Xn表示第n次映射函數值。

采用Tent混沌映射生成初始種群的步驟如下。

步驟1 在[0,1]內隨機生成初始值的初值X0[X0應避免落入小周期(0.2，0.4，0.6，0.8)]進入標志組，且S(1)=X0，i=j=1。

步驟2 利用式(10)進行迭代，產生新變量Xi，i=i+1。

步驟3 如果迭代達到最大次數，執行步驟5；若生成的X落入小周期點，則轉到步驟3；若未出現上述現象，執行步驟2。

步驟4 令Xi=S(j+1)=S(j)+ε，j=j+1，其中ε為隨機數,執行步驟2。

步驟5 程序運行停止，保存產生的混沌序列。

3.2 精英反向學習策略

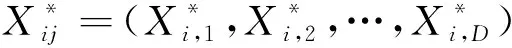
(11)

式(11)中：Xi,j為第j維個體的數值；α為區間[0,1]內服從正態分布的隨機數；(LBj,UBj)表示第j維搜索空間的動態邊界，其定義為

LBj=min(Xi,j)

(12)

UBj=max(Xi,j)

(13)

式中：min(Xi,j)、max(Xi,j)分別為第j維個體的最小值和最大值。

當生成的反向解超出(LBj,UBj)邊界范圍時，使用隨機生成的方法進行越界重置，具體描述為

(14)

綜合上述，改進的混沌精英黏菌算法(chaotic elite slime mould algorithm, CESMA)可以利用偽代碼表述其執行流程，如表1所示。

表1 CESMA算法偽代碼Table 1 Pseudo code of CEMSA algorithm

1.3 算法性能測試

為充分驗證CESMA算法的有效性和優越性，選取4個基準函數對改進CESMA算法、標準SMA算法、粒子群算法(particle swarm optimization, PSO)[22]、鯨魚優化算法(whale optimization algorithm, WOA)[8]以及多元宇宙算法(multi-verse optimizer, MVO)[23]進行性能對比。基準測試函數的表達式、維度、取值范圍和理論最優值如表2所示。表2中，Sphere(F1)和Rosenbrock(F2)為單峰函數，用于評價算法的收斂速度和優化精度；Griewank(F3)和Rastrigin(F4)為多峰函數，主要用來測試算法是否能夠避免局部最優，找到全局最優解；xi為各函數表達式在相應取值范圍內第i維度的數值，i∈[1,n]，n為設置的最大維度(即30)。

表2 基準測試函數Table 2 Benchmark functions

在相同實驗條件基礎上，所有算法參數均與原文獻保持一致，種群規模設置為50，最大迭代數為500次，采用MATLAB R2017a編程，計算機操作系統為Windows 10，處理器為Intel i5-10300H CPU @ 2.50 GHz，內存容量為16 GB。為減少隨機因素對測試結果的影響，5種算法分別對每個函數獨立運行30次，記錄求得最優函數值的平均值和標準差，測試結果如表3所示，尋優結果最好的算法已用粗體表示。

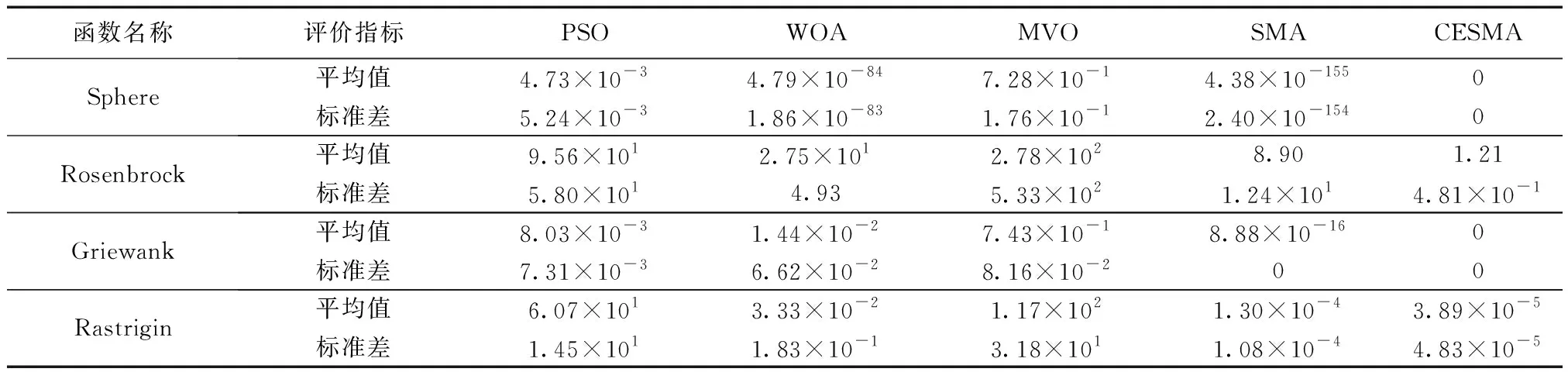
表3 不同算法性能測試對比結果Table 3 Comparison results of the performance of different algorithms

從表3可以看出：在Sphere函數上，CESMA的平均值和標準差均優于標準SMA和其他3種算法；Rosenbrock函數的全局最優值位于一個拋物線型的山谷中，部分智能優化算法很難找到，只有CESMA的結果最近理論最優解；在多峰函數Griewank和Rastrigin上，CESMA的表現依然具有明顯優勢。5種算法的收斂曲線如圖3所示，CESMA比其他4種算法中有著更快的收斂速度和更高的求解精度，進一步證明了改進策略的有效性以及算法的可行性。

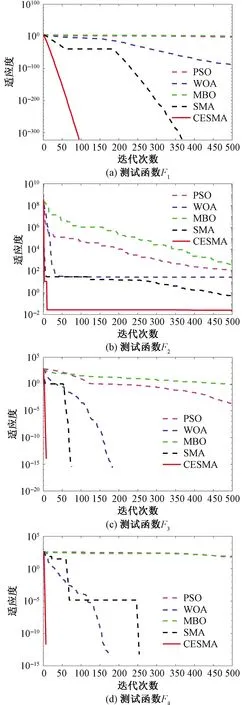
圖3 不同算法的收斂曲線Fig.3 Convergence curve of different algorithms

4 基于CESMA的轉速控制系統優化

4.1 CESMA-PID控制器設計

傳統PID控制器是通過調整系統實際輸出值與期望值產生的偏差量實現控制目標[24]，其數學模型為

(15)

式(15)中：u(t)為控制器輸出；e(t)為反饋誤差；Kp為比例增益系數；Ki為積分時間常數；Kd微分時間常數；不同的Kp、Ki、Kd組合對控制系統的穩定性、響應速度等都有著至關重要的影響，因此如何選擇一組最佳的合理控制參數使得系統綜合性能達到最優是PID控制的關鍵。

然而實際工業控制中，傳統PID控制器在高度非線性和不確定時參數難以整定，容易導致電機出現轉速超調顯著、轉矩波動明顯等問題[25]。根據以上理論分析，BLDCM轉速控制系統采用雙閉環控制：轉速外環采用CESMA動態優化的PID控制器(CESMA-PID)，電流內環采用電流滯環控制器，利用CESMA算法良好的優化搜索能力，能夠有效克服傳統參數整定方法的缺陷，實現電機平穩運行，如圖4所示。

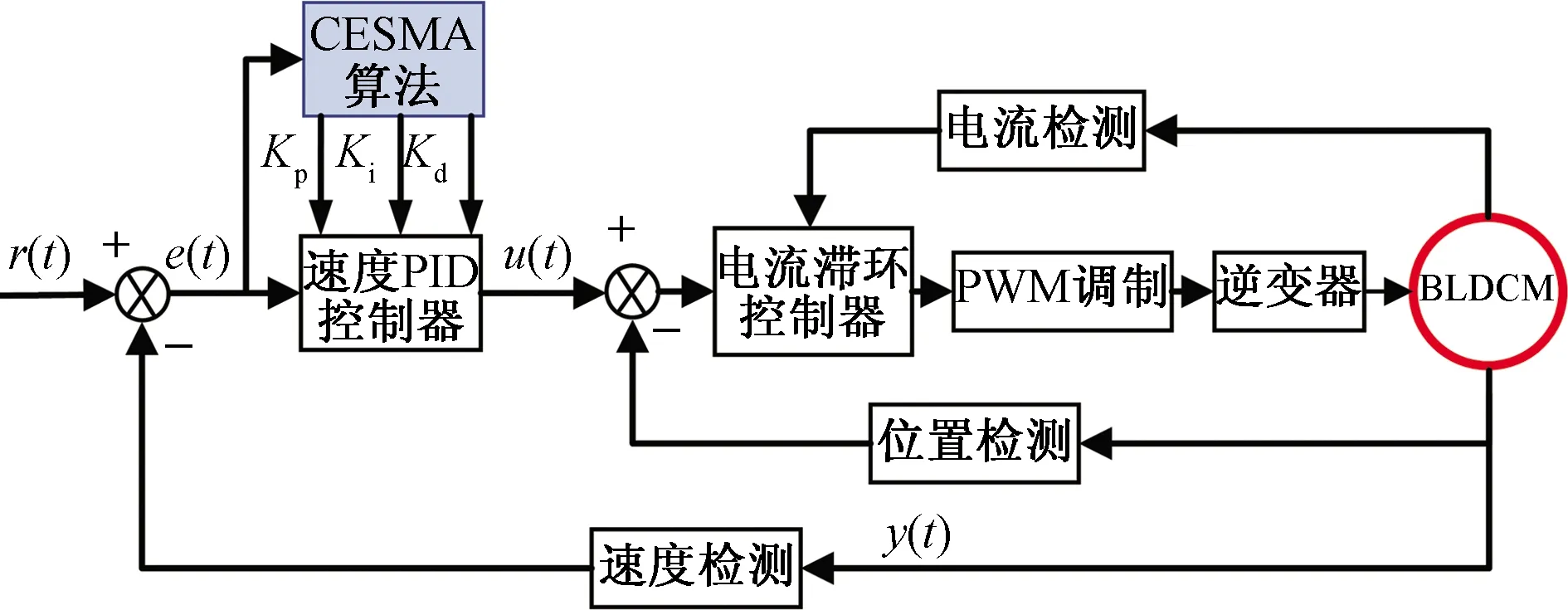
圖4 BLDCM轉速控制系統結構圖Fig.4 Structure diagram of BLDCM speed control system

e(t)=r(t)-y(t)

(16)

式(16)中：r(t)為電動機轉速值；y(t)為電機轉速反饋值。

根據BLDCM的控制要求，為了獲得滿意的動態特性本文選用誤差絕對值時間積分性能指標作為迭代尋優的適應度函數F主體部分，計算公式為

(17)

式(17)中：ω1、ω2為權重常數，取值范圍均在[0,1]；輸出u2(t)加入目的是防止控制性能過大。

同時針對超調現象，在性能指標中引入懲罰措施，將超調量作為目標函數中的一項，如式(18)所示：

e(t)<0

(18)

式(18)中：Δe(t)=y(t)-y(t-1)；ω3為權值常數，通常滿足ω3>>ω1，故取ω1=0.999，ω2=0.001，ω3=100。

4.2 CESMA-PID控制器實現步驟

采用CESMA算法優化PID控制器參數的具體實現步驟如下。

步驟1 設定種群規模，最大迭代次數，Kp、Ki、Kd的取值范圍以及空間維數，利用Tent混沌映射產生初始黏菌個體位置。

步驟2 將當前的黏菌個體位置作為PID參數，根據式(18)計算出個體適應度。

步驟3 更新當前最優個體和及其適應度值。

步驟4 根據式(8)計算W。

步驟5 對于每一個黏菌個體，根據式(6)、式(7)更新參數vb,vc和p，同時根據式(5)更新黏菌個體位置。

步驟6 利用精英反向學習策略產生新的解，更新當前最優個體及適應度值。

步驟7 若算法達到設定的最大迭代次數則輸出最優PID控制參數(即黏菌算法的全局最優位置)，否則返回步驟2。

步驟8 算法結束。

初始化種群規模為50，最大迭代次數為100次，空間維度D=3，Kp的取值范圍為[0,50]，Ki的取值范圍為[0,2]，Kd的取值范圍為[0,2]，運行CESMA算法對PID控制器進行優化，得到一組最佳系數為：Kp=35.58，Ki=0.856 7，Kd=0.282 6，同時可以計算出相應適應度函數值為14.454 4，如圖5所示。

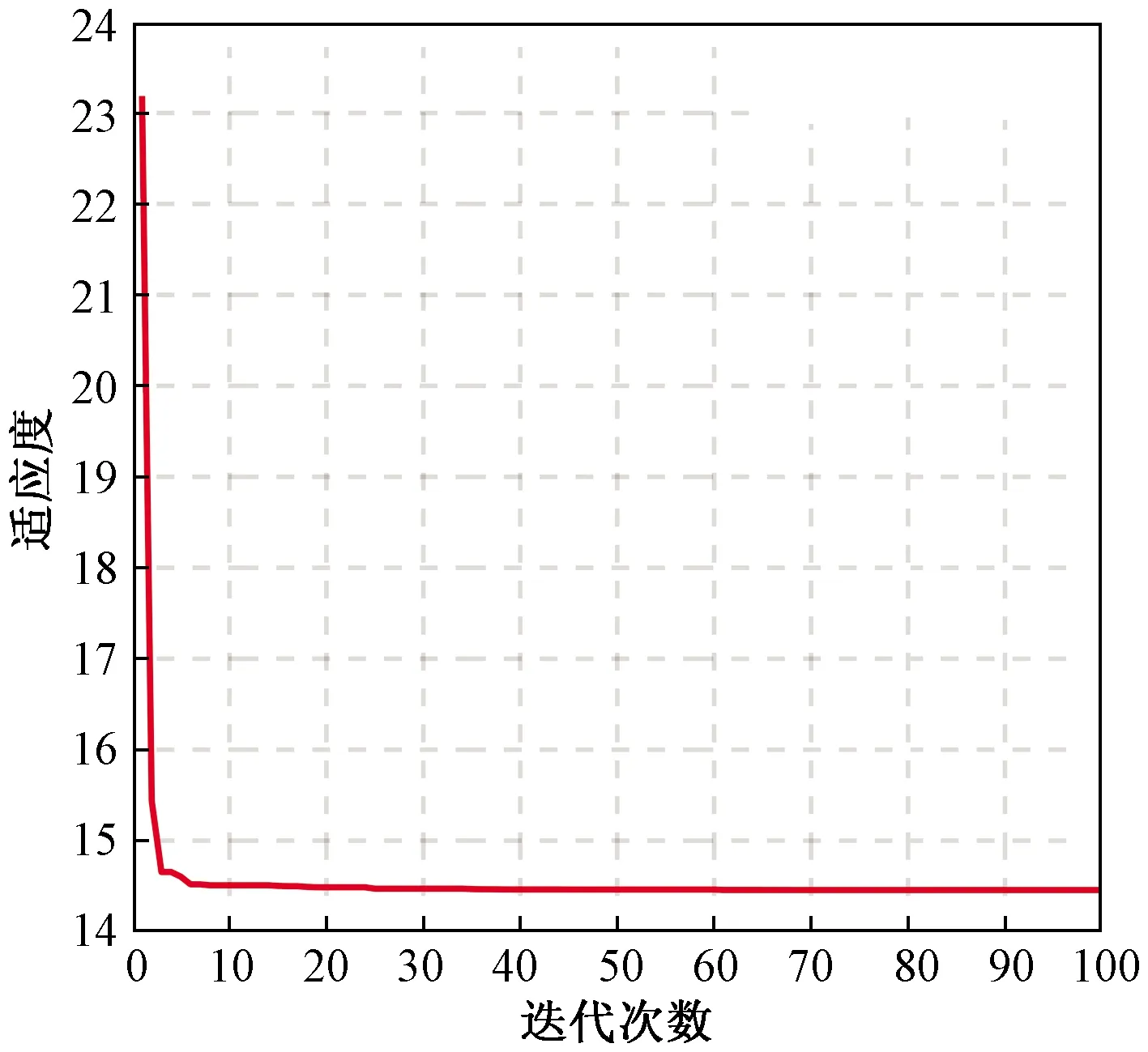
圖5 適應度函數曲線Fig.5 Fitness function curve

5 仿真及實驗

5.1 仿真分析

在MATLAB R2017a環境中，編寫S-Function函數和Simulink模塊相結合搭建BLDCM轉速控制系統仿真模型進行實驗，BLDCM仿真參數如表4所示。為了突出對比效果，仿真轉速環分別采用傳統PID、模糊PID以及CESMA-PID進行控制，傳統PID的初始值根據Ziegler-Nichols法獲得分別為：Kp=12.48，Ki=0.657，Kd=0.23；模糊PID采用三角形隸屬度函數，由MATLAB的FUZZY工具箱得到模糊規則方陣；CESMA-PID的參數設置同4.2節一致。

表4 BLDCM仿真參數Table 4 BLDCM simulation parameters

首先，系統在變速條件下進行實驗，設定空載起動時額定轉速n=1 000 r/min，在時間t=0.5 s時，轉速下降至n=600 r/min；在t=0.8 s時，加速到n=800 r/min，圖6為3種控制器下的轉速響應曲線。可以看出：在給定轉速設定為n=1 000 r/min時，CESMA-PID可在0.15 s達到穩定狀態，傳統PID及模糊PID的穩定時間較長均在0.3 s左右；在轉速突變為n=600 r/min時，CESMA-PID在0.05 s后重新達到穩態；當給定轉速提升為n=800 r/min時，CESMA-PID亦可在0.1 s內達到穩態。由此可見本文提出的CESMA-PID控制器響應速度更快，恢復穩定狀態用時最短，控制效果優于其他兩種控制方法。

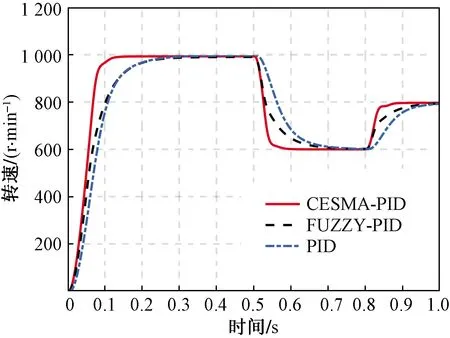
圖6 變速條件轉速響應曲線Fig.6 Speed response curve with different speed

其次，系統在突加負載條件下運行，設定空載起動時額定轉速n=1 000 r/min，在時間t=0.5 s時，加入擾動轉矩0.3 N·m，電機轉速響應曲線如圖7所示。當轉矩施加在0.5 s時，傳統PID和模糊PID均存在明顯擾動，而CESMA-PID的波動最小，恢復穩定狀態快，抗干擾能力強。

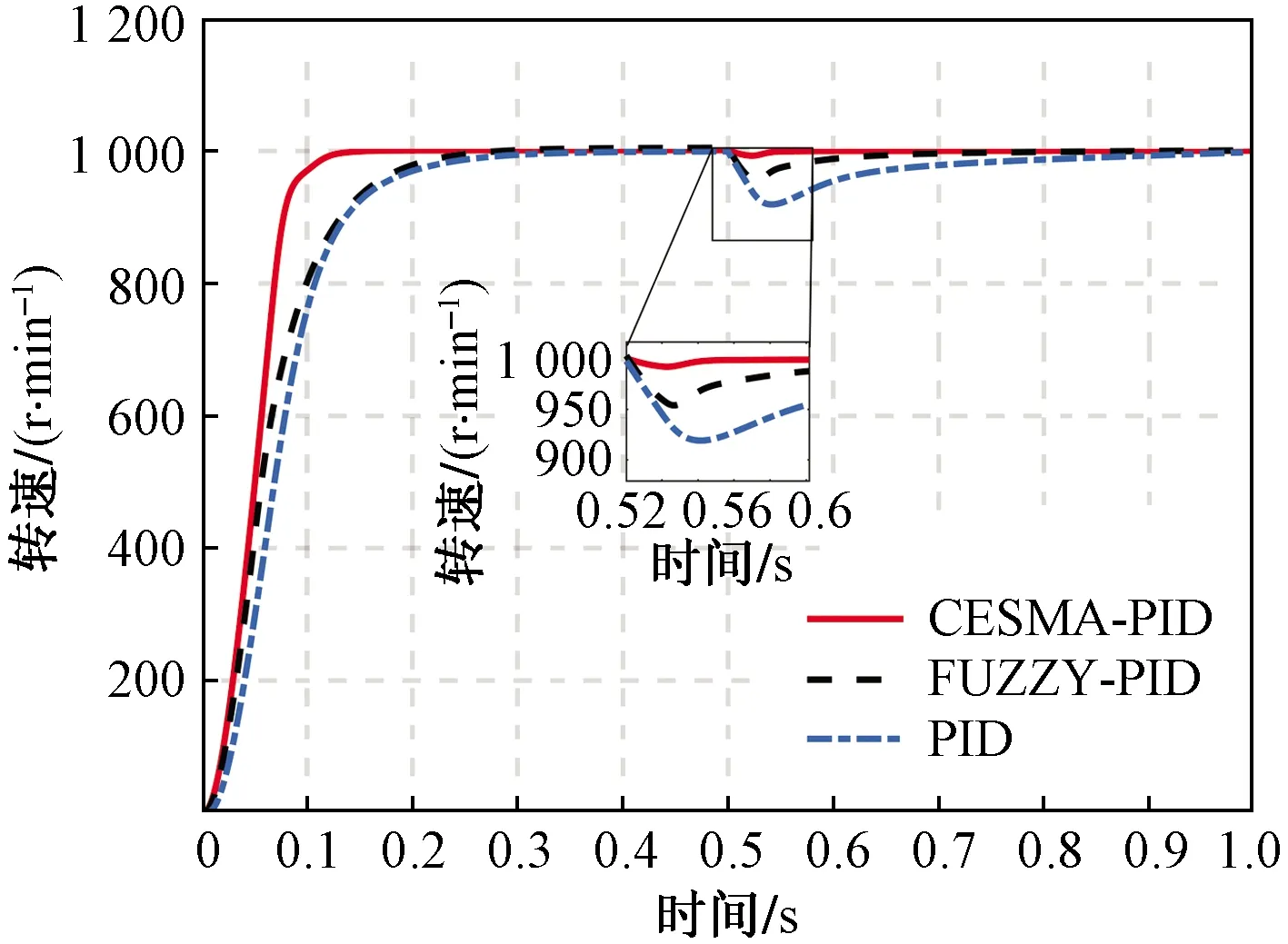
圖7 突加負載條件下轉速響應曲線Fig.7 Speed response curve under sudden load

最后，對CESMA-PID在轉速突變、突加負載條件下的控制性能進行仿真驗證，設定空載起動時額定轉速n=1 000 r/min，當系統運行到t=0.5 s時，轉速下降至n=800 r/min，同時加入0.3 N·m擾動轉矩，電機轉速響應曲線如圖8所示。可以看出，CESMA-PID沒有明顯超調且響應速度快，可以在0.05 s內達到穩定狀態，而傳統PID以及模糊PID的穩態時間較長分別為0.68 s和0.70 s。

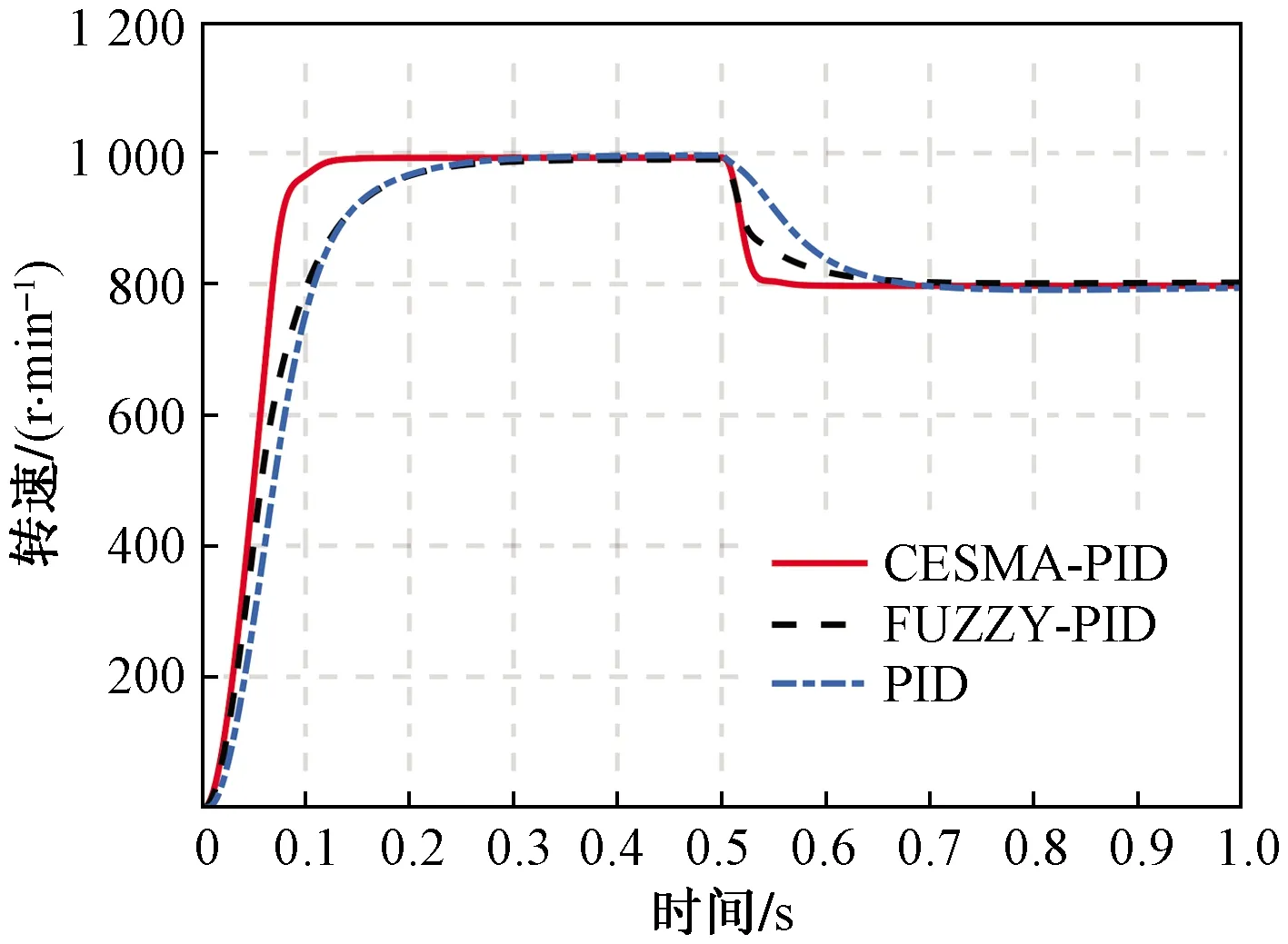
圖8 變速、突加負載條件下轉速響應曲線Fig.8 Speed response curve under different speed and sudden load

綜上仿真結果驗證了所提出的CESMA-PID控制器要比傳統PID控制器和模糊PID控制器有著更快的響應速度，更高的控制精度和更強的抗干擾能力。

5.2 實驗驗證

為進一步驗證仿真模型的可靠性，搭建了基于意法半導體公司STM32F103ZET6單片機的BLDCM轉速控制系統實驗平臺，系統硬件組成如圖9所示。實驗所用電機主要規格參數如下：額定電壓為24 V、額定功率為100 W、額定轉速為3 000 r/min、空載電流為0.8 A、極對數為4。

圖9 BLDCM轉速控制系統硬件組成Fig.9 Hardware composition of BLDCM speed control system

實驗時，令參考給定轉速由1 000 r/min下降至600 r/min，經過0.3 s后，再由600 r/min恢復至1 000 r/min，將采集的數據結果以十進制導入MATLAB軟件中，3種控制方法對電機的轉速控制跟隨曲線如圖10所示。可以看出，傳統PID和模糊PID控制下的電機轉速存在超調，穩定時間長，且轉速曲線存在一定抖動；而基于本文改進黏菌算法自整定PID控制下的電機轉速無超調，轉速曲線相對平滑，實驗結果再次證明經過CESMA算法優化后的PID控制器動靜態性能有著顯著提高。

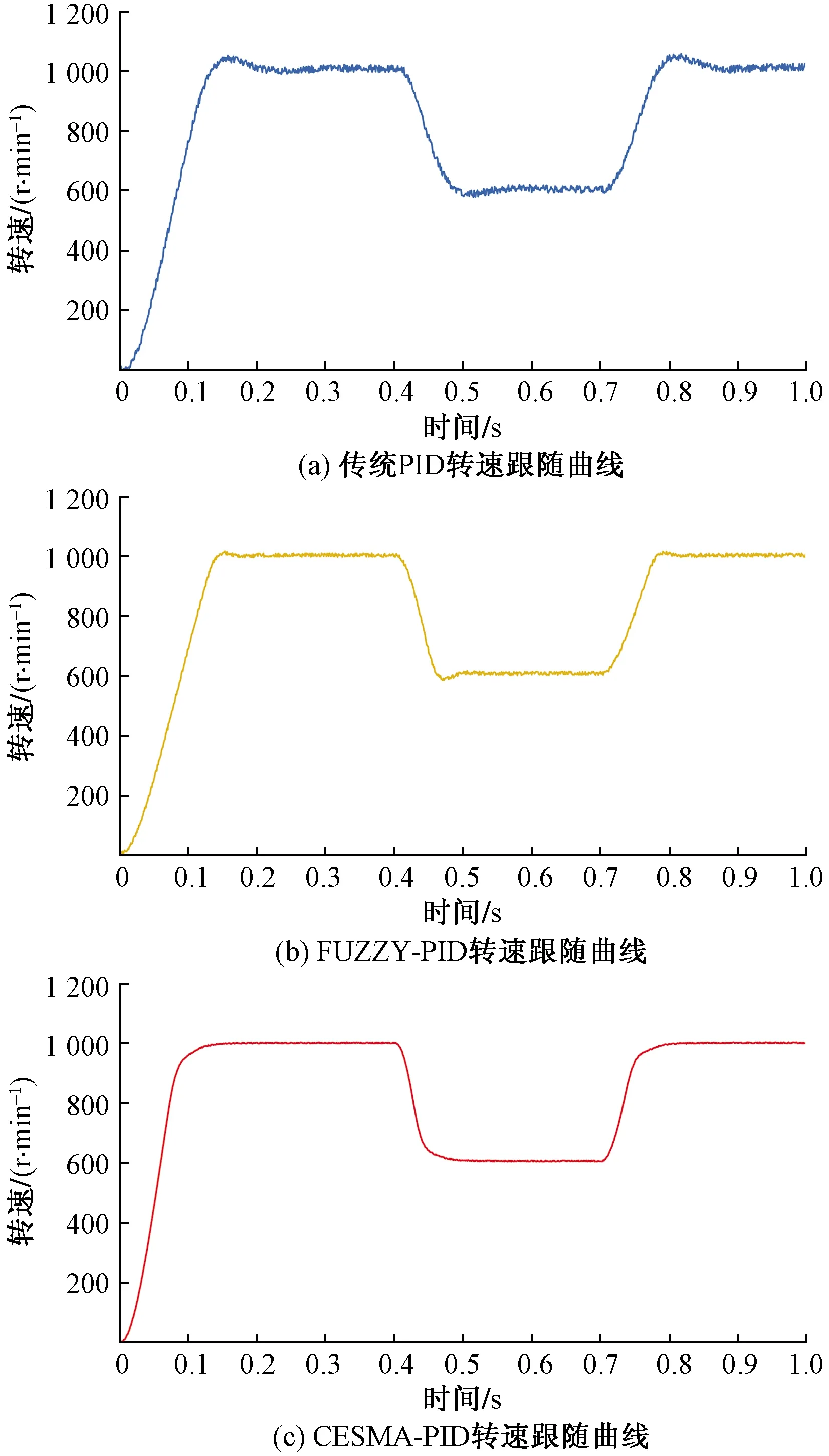
圖10 不同控制方法下的轉速跟隨曲線Fig.10 Speed following curve of different control methods

6 結論

為提高無刷直流電機轉速控制性能，提出了一種混沌精英黏菌算法優化的自適應PID控制方法。通過4種典型測試函數驗證了改進算法在收斂速度和尋優精度上的優越性，并將其應用于無刷直流電機速度環PID控制器參數自整定。分別在變速、突加負載以及變速與負載共同作用的條件下進行仿真和實驗，結果表明本文方法具有響應速度快、超調量小、魯棒性較強等優勢，在其他PID控制的系統中也有著良好的應用前景。