汾渭平原SO2與氣溫的函數(shù)型空間自回歸分析

胡錫健， 李妍琳， 石小平

(新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院， 烏魯木齊 830046)

在中國經(jīng)濟由高速增長階段轉(zhuǎn)向高質(zhì)量發(fā)展階段過程中，環(huán)境治理和污染防治是一道重要關(guān)口。近年來，推進大氣污染防治工作卓有成效,京津冀地區(qū)空氣質(zhì)量顯著提升，長三角、珠三角地區(qū)空氣質(zhì)量持續(xù)達標，汾渭平原卻成為中國空氣污染最嚴重的區(qū)域之一，引起國家和社會的高度重視[1]。2018年7月，在《打贏藍天保衛(wèi)戰(zhàn)三年行動計劃》中，汾渭平原被納入環(huán)境污染三大重點防控區(qū)域之一，成為藍天保衛(wèi)戰(zhàn)的“主戰(zhàn)場”。

汾渭平原能源結(jié)構(gòu)以煤為主，煤炭在能源消費中占約90%，遠高于全國平均水平(60%)，煤煙型污染特征明顯，大氣中的主要污染物有二氧化硫、二氧化氮、可吸入顆粒物等,這不僅對健康帶來了很大的危害，還影響著人們的正常生活。

大氣污染狀況與當?shù)氐臍庀髼l件有著密切的關(guān)系。繆明榕等[2]分析了南通市2018年大氣污染物與氣象因素的關(guān)系。張岳軍等[3]、張連華等[4]分別對汾渭平原SO2和NO2進行時空分布特征分析，研究該區(qū)域的SO2、NO2的污染狀況，全面了解汾渭平原SO2、NO2的時空變化特征，對有效治理大氣污染具有重要意義。

氣象數(shù)據(jù)在時間尺度上有明顯的函數(shù)特征，汾渭平原11個城市的逐時氣溫數(shù)據(jù)一年有9萬多條，面對如此龐大的數(shù)據(jù)集，傳統(tǒng)的數(shù)據(jù)分析方法不能對這些數(shù)據(jù)直接處理。函數(shù)型數(shù)據(jù)分析(functional data analysis，F(xiàn)DA)方法專門針對此類數(shù)據(jù)，采用平滑方法將其擬合成曲線再進行分析。Ramsay[5]于1982年率先提出一種全新的數(shù)據(jù)分析思路——函數(shù)型數(shù)據(jù)分析；Ramsay等[6]對函數(shù)型數(shù)據(jù)做了進一步詳細的描述并講述了諸多關(guān)于FDA的應(yīng)用。與傳統(tǒng)方法相比，函數(shù)型數(shù)據(jù)分析方法不僅在處理高維觀測數(shù)據(jù)上能給出更加合理的直觀解釋，而且在分析數(shù)據(jù)時能保留更多的數(shù)據(jù)信息，從而得到更精確的分析結(jié)果。因此，F(xiàn)DA應(yīng)用于許多學(xué)科領(lǐng)域，如生物學(xué)、醫(yī)學(xué)、氣象學(xué)、計量經(jīng)濟學(xué)、金融、化學(xué)計量學(xué)和地球物理學(xué)等[7-8]。函數(shù)型回歸分析是FDA最重要的應(yīng)用之一，經(jīng)典函數(shù)型線性回歸模型(functional linear model，F(xiàn)LM)是函數(shù)型線性回歸的最簡單形式。Paganoni等[9]給出了概述，在FDA研究領(lǐng)域受到廣泛關(guān)注。在對FLM進行參數(shù)估計時；Cardot等[10]首次研究函數(shù)型線性回歸模型，利用函數(shù)型主成分分析方法給出斜率函數(shù)估計的收斂速度；Hall等[11]基于函數(shù)型主成分分析方法和最小二乘估計方法給出函數(shù)型線性回歸模型的估計。在做FLM分析時假設(shè)所有個體都是相互獨立的，但是在信息技術(shù)的飛速發(fā)展今天，區(qū)域之間的相關(guān)性信息逐漸顯現(xiàn)，具有空間結(jié)構(gòu)的數(shù)據(jù)越來越普遍。在這些數(shù)據(jù)中，響應(yīng)變量由于空間結(jié)構(gòu)而存在較強的相關(guān)性，如果使用FLM來分析帶有空間相關(guān)性的數(shù)據(jù)，可能無法充分利用數(shù)據(jù)中包含的信息。當協(xié)變量為標量時，通常使用空間自回歸(spatial autoregression，SAR)模型來擬合這類具有空間相關(guān)性的數(shù)據(jù)。SAR模型是處理空間相關(guān)問題的一種有效方法。

Cliff等[12]在空間自回歸的一般模型、參數(shù)估計和假設(shè)檢驗方面有了開拓性的進展；Anselin[13]提出了空間自回歸的一般模型。近年來，SAR模型的應(yīng)用越來越廣泛；Kanaroglou等[14]將SAR模型用于估計SO2的空氣污染濃度.在環(huán)境學(xué)領(lǐng)域與氣象學(xué)領(lǐng)域中，觀測數(shù)據(jù)會有曲線形式。因此，將SAR模型的數(shù)據(jù)類型擴展到函數(shù)型數(shù)據(jù)越來越迫切。Ahmed[15]首次提出了函數(shù)型空間自回歸模型(functional spatial autoregressive model，F(xiàn)SAR)，并利用極大似然估計方法對FSAR模型進行估計，并證明了該模型中參數(shù)的漸進性質(zhì)；Huang等[16]通過借鑒SAR模型的概念，利用空間相關(guān)系數(shù)和權(quán)重矩陣將具有空間結(jié)構(gòu)的數(shù)據(jù)融入FLM模型中，稱該模型為空間函數(shù)型線性模型(spatial functional linear model，SFLM)，并利用該模型分析了2005—2007年中國34個主要城市年均降水量與月均溫度的關(guān)系；應(yīng)彩云[17]將函數(shù)型變量引入一般的SAR模型中，構(gòu)建半泛函SAR模型，并研究相應(yīng)的參數(shù)估計方法。汾渭平原作為中國的四大平原之一，有著嚴重的大氣污染問題，但目前還沒有學(xué)者函數(shù)型回歸模型分析該區(qū)域的空氣質(zhì)量數(shù)據(jù)與氣象數(shù)據(jù)之間的關(guān)系。從汾渭平原11個城市的空間分布來看，空氣質(zhì)量數(shù)據(jù)中必然有部分數(shù)據(jù)存在空間相關(guān)性，結(jié)合SAR和FLM分析方法，采用FSAR模型探討該地區(qū)空氣質(zhì)量與氣象的關(guān)系不僅能充分利用數(shù)據(jù)的空間自相關(guān)和高維連續(xù)性特征，而且提供分析汾渭平原大氣污染情況的新途徑。

采用2019年汾渭平原11個城市的空氣質(zhì)量數(shù)據(jù)[PM2.5、PM10.0、SO2、NO2、O3和CO的監(jiān)測數(shù)據(jù)及空氣質(zhì)量指數(shù)(air quality index，AQI)]，運用空間自相關(guān)Moran’sI檢驗對這7項數(shù)據(jù)做空間自相關(guān)分析，選擇檢驗結(jié)果最顯著指標作為響應(yīng)變量，并采用2019年該區(qū)域11個城市的逐小時氣溫，應(yīng)用函數(shù)型空間自回歸方法構(gòu)建空氣質(zhì)量數(shù)據(jù)與氣溫的FSAR模型。定量分析汾渭平原11個城市空氣質(zhì)量數(shù)據(jù)與氣溫的相關(guān)性，并與普通的函數(shù)型回歸模型進行比較分析。

1 數(shù)據(jù)說明與方法

1.1 研究數(shù)據(jù)

選取汾渭平原(包括河南省洛陽市、三門峽市，陜西省西安市、咸陽市、寶雞市、銅川市、渭南市，山西省呂梁市、晉中市、臨汾市、運城市) 11 個市作為研究對象, 整理了2019年汾渭平原地區(qū)11個城市的7項空氣質(zhì)量數(shù)據(jù)[PM2.5、PM10.0、SO2、NO2、O3和CO的監(jiān)測數(shù)據(jù)及空氣質(zhì)量指數(shù)(AQI)]和氣象數(shù)據(jù)(地表氣溫)，數(shù)據(jù)分別來自中國空氣質(zhì)量在線監(jiān)測分析平臺和美國國家航空航天局MERRA2中的inst1_2d_asm_Nx文件集。汾渭平原11個城市在空間上的分布如圖1所示。

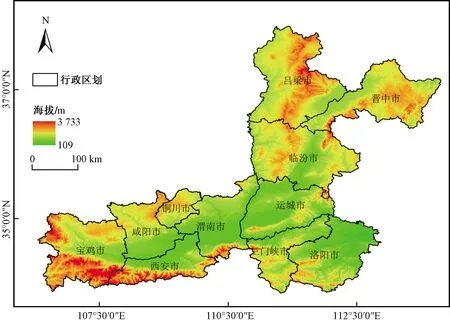
圖1 汾渭平原地形圖Fig.1 Topographic map of Fenwei plain

1.2 函數(shù)型空間自回歸模型

FSAR的一般形式為

(1)

式(1)中：x(t)=[x1(t),x2(t),…,xn(t)]T,t∈T為函數(shù)型協(xié)變量，t表示某一時間段，T為整個時間段；y=(y1,y2,…,yn)T為標量響應(yīng)變量；β(t)表示斜率函數(shù)；ρ為空間相關(guān)系數(shù)；W為空間權(quán)重矩陣；ε為殘差項，并假設(shè)ε服從多元正態(tài)分布N(0,σ2I)，其中σ2為殘差的方差，I為單位矩陣。

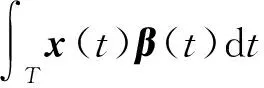
1.2.1 函數(shù)型主成分基展開

假設(shè)總體為x(t)，記K(s,t)=Cov[x(s),x(t)]為x(t)的協(xié)方差函數(shù)，根據(jù)Mercer’s 引理有協(xié)方差函數(shù)的譜分解，可表示為[16]

(2)

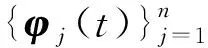
第i個觀測值xi(t)的Karhumen-Loéve展開式可表示為

(3)

在實際應(yīng)用中，φj(t)是未知的，因此通過樣本協(xié)方差函數(shù)的譜分解來估計特征函數(shù)φj(t)，即考慮樣本協(xié)方差陣，可表示為

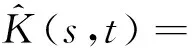
(4)

(5)

式(5)中：aj=(a1j,a2j,…,anj)T。

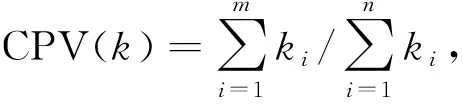
(6)

1.2.2 FSAR模型的極大似然估計

根據(jù)近似FSAR模型[式(6)]，用極大似然方法估計未知參數(shù)，令A(yù)=(aij)n×m，b=(b1,b2,…,bm)T，從而式(6)可寫為

y≈ρWy+Ab+ε

(7)

基于前面的假設(shè)ε服從多元正態(tài)分布N(0,σ2I)，y的似然函數(shù)為

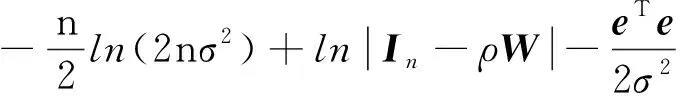
(8)

式(8)中：e=y-ρWy-Ab，先給定ρ，可得到b和σ2的極大似然估計分別為

(9)

(10)

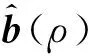
(11)

通過最大化式(11)，可求得ρ的估計量為

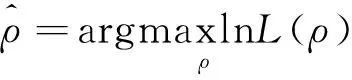
(12)

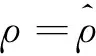
(13)

2 汾渭平原SO2與氣溫的函數(shù)型空間 自回歸分析

分別對2019年汾渭平原地區(qū)11個城市的7項空氣質(zhì)量數(shù)據(jù)[PM2.5、PM10.0、SO2、NO2、O3和CO的監(jiān)測數(shù)據(jù)及空氣質(zhì)量指數(shù)(AQI)]，運用R、Geoda等軟件進行空間自相關(guān)分析，采用rook矩陣為空間權(quán)重矩陣。首先對年均空氣質(zhì)量進行空間自相關(guān)分析，年均空氣質(zhì)量的空間相關(guān)性是否顯著，由Moran’sI指數(shù)驗證，結(jié)果如表1所示。

表1結(jié)果顯示：這7項空氣質(zhì)量數(shù)據(jù)中SO2濃度和O3具有較強的空間自相關(guān)性，且SO2濃度的空間自相關(guān)性非常顯著，P遠小于0.05。選取7項空氣質(zhì)量數(shù)據(jù)中的SO2濃度數(shù)據(jù)與氣溫數(shù)據(jù)進行函數(shù)型空間自回歸分析。由于所研究的是2019年每月SO2濃度與該月氣溫之間的關(guān)系，故對每月的SO2濃度進行Moran’sI檢驗，如表2所示，結(jié)果顯示每個月這11個城市的SO2濃度都具有很強的空間自相關(guān)性，這說明運用FASR模型分析方法是合理有效的。

表1 2019年汾渭平原11個城市的年均空氣 質(zhì)量Moran’s I值Table 1 Moran’s I value of annual average air quality of 11 cities in Fenwei Plain in 2019

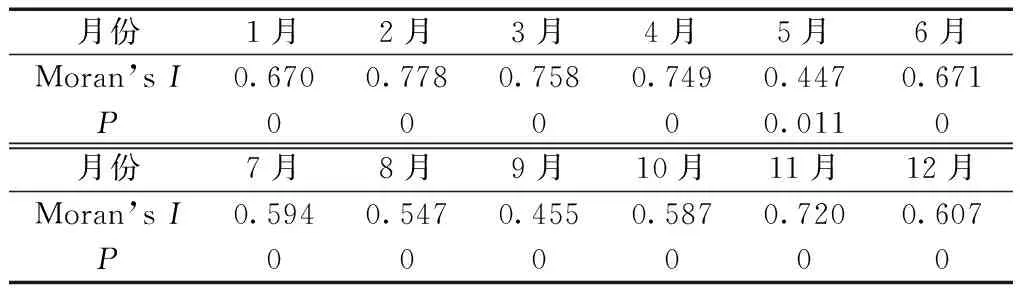
表2 2019年汾渭平原11個城市SO2月均Moran’s ITable 2 Monthly average of Moran’s I in SO2 in 11 cities in the Fenwei Plain in 2019

2.1 氣溫曲線的動態(tài)分析

選取汾渭平原11個城市2019年的逐時氣溫數(shù)據(jù)和逐月SO2濃度數(shù)據(jù)，觀察發(fā)現(xiàn)收集到的逐時氣溫數(shù)據(jù)具有周期性，故采用傅里葉基樣條函數(shù)擬合2019年每月的逐時氣溫曲線xi(t)，i=1,2,…,11，并將其作為函數(shù)型空間自回歸模型的協(xié)變量，平滑曲線如圖2所示，為驗證原始數(shù)據(jù)與平滑曲線之間的擬合效果，計算各月擬合曲線的均方根誤差(root mean squared error,RMSE)，結(jié)果如表3所示。

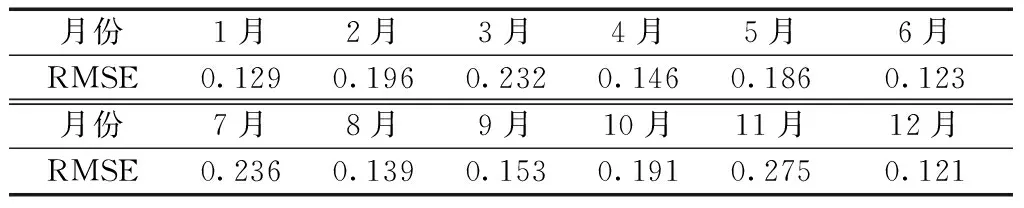
表3 各月份擬合曲線的均方根誤差Table 3 RMSE of the fitted curve for each month

從圖2可以看出，2019年汾渭平原11個城市的溫度變化趨勢大體相似，每日氣溫呈周期性變化。汾渭平原一年四季溫差較大，冬冷夏熱，最高溫出現(xiàn)在8月份，最低溫出現(xiàn)在1月份。1—7月溫度持續(xù)上升，8月達到最大，之后溫度又持續(xù)下降。通過導(dǎo)函數(shù)刻畫了氣溫的動態(tài)變化特征，如一階導(dǎo)函數(shù)(圖3)及二階導(dǎo)函數(shù)(圖4)所示。

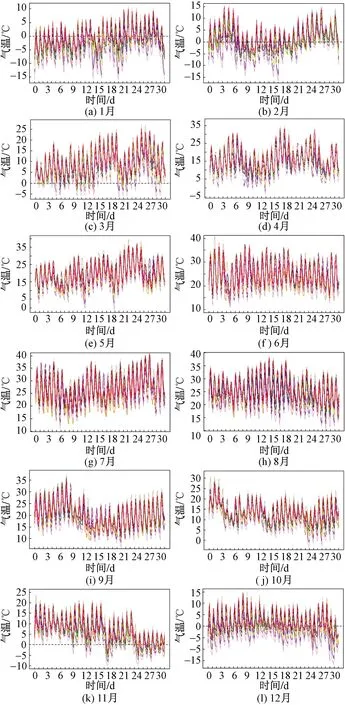
圖2 2019年每月逐時氣溫變化曲線Fig.2 Hourly temperature change curve of each month in 2019

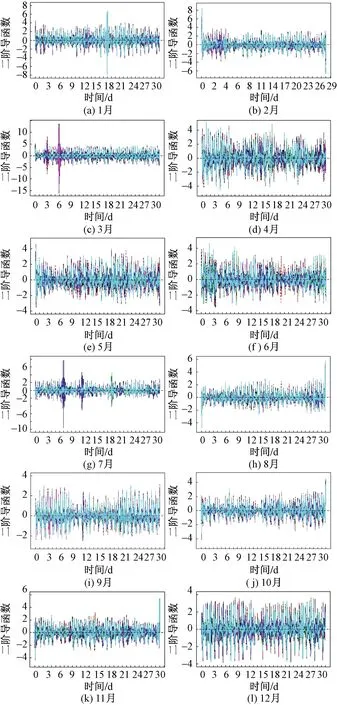
圖4 11個城市每月溫度曲線的二階導(dǎo)函數(shù)Fig.4 The second derivative function of monthly temperature curve in 11 cities

圖3為溫度曲線的一階導(dǎo)函數(shù)圖，表示的是溫度的上升或下降狀態(tài)，一階導(dǎo)函數(shù)大于零時溫度上升，小于零時溫度下降。圖4為溫度曲線的二階導(dǎo)函數(shù)圖，表示溫度上升或下降速度的快慢。從圖中可以發(fā)現(xiàn)，11個城市每日的溫度上升和下降的變化相似，3、4、5月的一階導(dǎo)函數(shù)圖波動較大，這說明這3個月的每日溫度變化較大，且當月的最低溫與最高溫相差30 ℃左右。

2.2 函數(shù)型空間自回歸分析

利用前面所述的函數(shù)型空間自回歸分析方法，基于R語言編寫的程序?qū)崿F(xiàn)汾渭平原11個城市的SO2濃度與氣溫曲線的函數(shù)型空間自回歸實證分析。以2019年每月的逐時氣溫曲線xi(t)，i=1,2,…,11為函數(shù)型空間自回歸模型的協(xié)變量，月均SO2濃度yi為響應(yīng)變量，建立函數(shù)型空間自回歸(FSAR)模型為

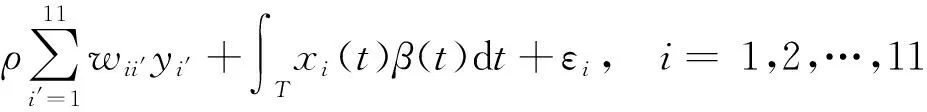
(14)

式(14)中：yi′為第i′個城市的月均SO2濃度；wii′為城市i和i′之間的權(quán)重；εi為第i個等式對應(yīng)的殘差。

為了分析汾渭平原11個城市之間的SO2濃度存在空間自相關(guān)性，同時考慮普通的函數(shù)型線性模型(functional linear model，F(xiàn)LM)為

(15)

式(15)中：響應(yīng)變量yi和函數(shù)型協(xié)變量xi(t)分別表示2019年第i個城市的月均SO2濃度和該月對應(yīng)的逐時氣溫曲線；β(t)、γ(t)為斜率函數(shù)。

為了估計式(14)、式(15)中的斜率函數(shù)β(t)、γ(t)，使用函數(shù)型主成分分析降維， 基于主成分基函數(shù)的FSAR模型和FLM分別表示為

(16)

(17)

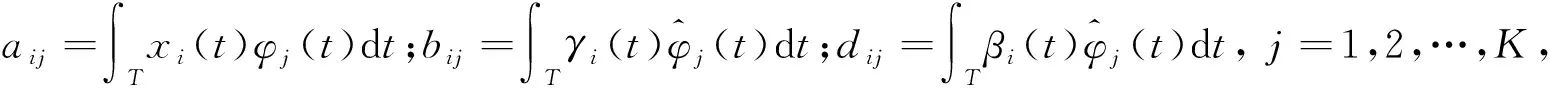
首先利用函數(shù)型主成分分析方法對2019年汾渭平原11個城市12個月的氣溫變化曲線分別提取了前4個主成分，特征值及其累積方差貢獻率如表4所示。

根據(jù)表4發(fā)現(xiàn)當取前4個主成分時累積方差貢獻率均在94%以上，包含了數(shù)據(jù)足夠多的信息。基于函數(shù)型主成分分析對氣溫函數(shù)完成降維，將無限維的FSAR模型轉(zhuǎn)換為了空間自回歸模型和函數(shù)型線性模型轉(zhuǎn)換為了多元線性模型，可表示為

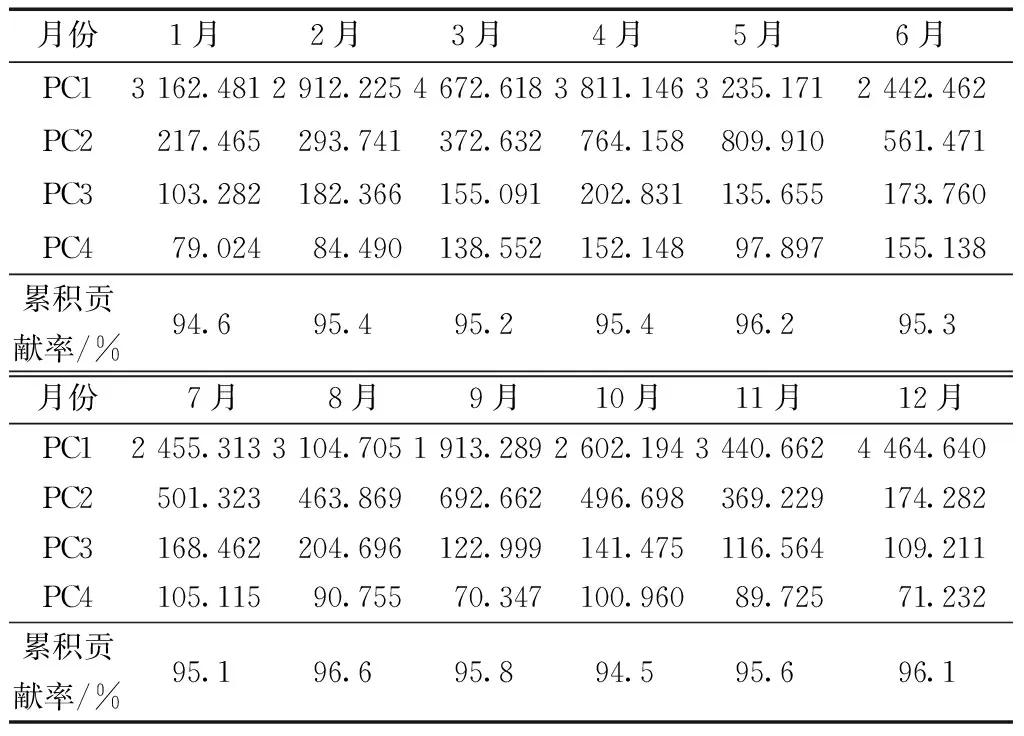
表4 函數(shù)型主成分分析特征值及其累積貢獻率Table 4 Functional principal component analysis characteristic values and their cumulative contribution rate

(18)

(19)

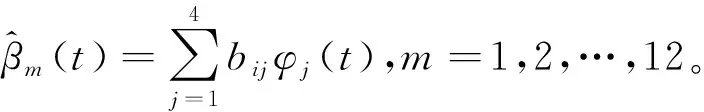
采用1.2節(jié)介紹的估計方法進行函數(shù)型空間自回歸分析，并對β(t)進行估計，斜率函數(shù)的估計結(jié)果如圖5所示。

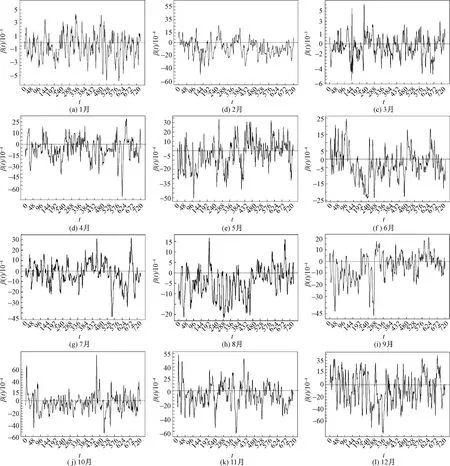
圖5 每月FSRA模型的斜率函數(shù)β(t)Fig.5 Slope function β(t) of monthly FSRA model

觀察圖5可知，每月β(t)為負的區(qū)域均大于β(t)為正的區(qū)域，這說明從整體上看氣溫與SO2濃度呈負相關(guān)，并結(jié)合圖3每月氣溫一階導(dǎo)函數(shù)圖像可以發(fā)現(xiàn)，氣溫上升時，對SO2濃度的負影響較小，氣溫下降時，對SO2濃度的負影響較大，2月的β(t)為負的面積在全年中是最小的，其次是1月、8月的β(t)為負的區(qū)域在全年中是最大的，其次是7月。從每天的溫度變化趨勢來看，氣溫每日呈周期性變化，其對SO2濃度的負影響也呈周期性變化，在每日氣溫上升的時間段內(nèi)，對SO2濃度的負影響比較小，在溫度下降的時間段內(nèi)，對SO2濃度的負影響較大。

根據(jù)表5均方誤差(mean absolute error，MSE)可知，F(xiàn)SAR模型擬合的響應(yīng)變量MSE明顯低于FLM的MSE，這說明FSAR的擬合效果更好，這兩種方法的MSE平均相差7倍以上，12月份的差別最大。從圖6可以看出，F(xiàn)SAR與FLM之間的差異，同時觀察到FLM模型的MSE在全年呈現(xiàn)明顯的季節(jié)性差異，在冬季MSE很大，夏季很小，很大一部分原因是由于汾渭平原冬季供暖[19]這一人為因素造成，而FSAR并沒有很明顯的這類變化規(guī)律，這說明FSAR模型降低了人為因素的誤差影響。冬季FSAR模型效果明顯,而FLM擬合的MSE 全年遠大于20，這說明FSAR 模型能夠很好地反映汾渭平原11 個城市的2019每月SO2濃度之間的空間自相關(guān)性，而FLM不能有效地解決這種相關(guān)性。可見，面對具有空間屬性的數(shù)據(jù)時，函數(shù)型空間自回歸模型擬合效果更好。

表5 FSAR模型與FLM模型的響應(yīng)變量均方誤差比較Table 5 Comparison of mean square error of response variables between FSAR model and FLM model

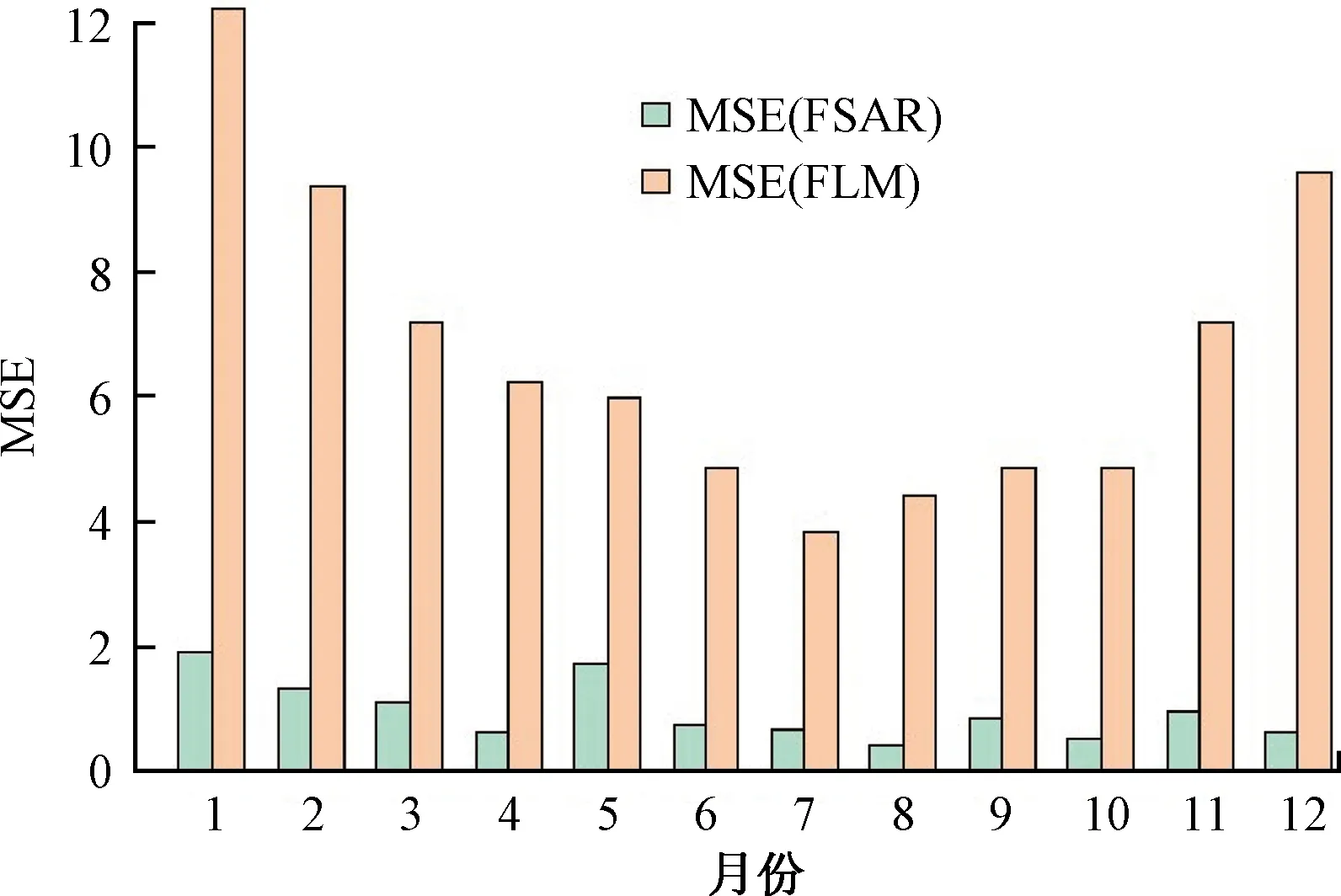
圖6 每月FSAR模型與FLM模型SO2濃度均方 誤差直方圖Fig.6 Monthly mean square error histogram of SO2 concentration in FSAR model and FLM model

3 結(jié)論

借助函數(shù)型數(shù)據(jù)分析的思想并與空間自回歸模型結(jié)合，針對汾渭平原特殊的地理位置和空氣質(zhì)量數(shù)據(jù)與氣象數(shù)據(jù)的關(guān)系，運用函數(shù)型空間自回歸模型分析該區(qū)域2019每月SO2濃度與當月氣溫曲線的關(guān)系。由于氣溫數(shù)據(jù)是每小時觀測一次，數(shù)據(jù)觀測頻率高且密集，而SO2濃度數(shù)據(jù)為月均數(shù)據(jù)，具有顯著的空間相關(guān)性，為了不丟失數(shù)據(jù)中包含的大量信息，將溫度數(shù)據(jù)擬合成函數(shù)曲線，把它看成隨機向量，此時選擇函數(shù)型線性模型和函數(shù)型空間自回歸模型來處理這組數(shù)據(jù)。通過函數(shù)型數(shù)據(jù)分析與空間自回歸模型結(jié)合的方式對汾渭平原的SO2與氣溫進行函數(shù)型空間自回歸分析，得到如下結(jié)論。

(1)從空間自相關(guān)分析中可以看出，汾渭平原地區(qū)各市的SO2濃度和氣溫除了受本市影響之外，還均受相鄰城市SO2濃度的影響，甚至比本市的影響更大。

(2)在運用函數(shù)型數(shù)據(jù)分析方法對逐時氣溫數(shù)據(jù)進行擬合成氣溫曲線后，對氣溫曲線求一階導(dǎo)數(shù)和二階導(dǎo)數(shù)，一階導(dǎo)數(shù)顯示汾渭平原氣溫呈周期性上升和下降，個別城市出現(xiàn)氣溫急劇變化情況。

(3)通過FSAR模型中系數(shù)函數(shù)β(t)的圖像可以看出，氣溫曲線與SO2濃度之間有顯著的負相關(guān)性。對比函數(shù)型空間自回歸模型和函數(shù)型線性模型，可以發(fā)現(xiàn)FSAR模型能夠很好地反映汾渭平原11個城市的2019每月SO2濃度之間的空間自相關(guān)性，擬合效果更好。

(4)函數(shù)型空間自回歸模型不僅能在宏觀上分析全年氣溫的變化對SO2濃度，而且在微觀上針對每小時的氣溫變化對SO2濃度的影響也清晰可見。并且通過對比FLM和FSAR的MSE，發(fā)現(xiàn)FSAR模型大大降低了人為因素所帶來的誤差。

氣溫曲線和SO2濃度是研究大氣污染的兩個重要指標。隨著收集數(shù)據(jù)的方法越來越精細化，學(xué)者們不僅在意宏觀上數(shù)據(jù)信息，更重視微觀上的分析所帶來更多更精確的信息，因此高頻數(shù)據(jù)的處理方法變得至關(guān)重要，函數(shù)型數(shù)據(jù)分析方法也受到人們的普遍關(guān)注。將函數(shù)型數(shù)據(jù)與帶有地理信息的數(shù)據(jù)結(jié)合，分析它們的空間分布特征和規(guī)律，函數(shù)型空間自回歸將成為近代氣候工作者關(guān)心的一個重要方向。