基于BP神經網絡的改良鹽漬土強度預測研究

李治斌，袁立月，丁 黔，張淼鑫，王紅梅

(1.黑龍江大學 建筑工程學院，黑龍江 哈爾濱 150080；2.黑龍江大學 水利電力學院，黑龍江 哈爾濱 150080)

鹽漬土廣泛分布在我國不同地區，總面積約占我國國土面積的2%[1]，而鹽漬土本身具有溶陷、鹽脹或腐蝕等性質[2]，力學和工程性質不佳，因此，十分有必要對改良鹽漬土展開深入的研究。

近年來，不少學者對凍結土和改良土單軸試驗的數學模型進行了研究。陳鑫[3]研究了尺寸和加載速率對凍結水泥土單軸壓縮影響，發現凍結水泥土的破壞應變隨溫度的降低和加載速率的增加而增大，在1.94%～6.94% 之間變化，不同加載速率條件下破壞應變與溫度呈冪函數關系，并建立了溫度和加載速率對水泥土單軸抗壓強度的數學預測模型和支持向量機的預測模型。曹智國[4]根據水泥土無側限抗壓強度試驗，提出一個綜合反映水泥摻入量、養護齡期以及孔隙率等因素對水泥土強度影響規律的綜合表征參數，水泥加固土和水泥穩定土的強度均與綜合表征參數呈冪函數關系。

而影響鹽漬土強度的因素有很多，這些影響因素與強度之間的關系往往是非線性的，難以用準確的數學模型來表達，所以越來越多的學者利用神經網絡來建立所需的預測模型。如宋啟卓等[5]利用BP神經網絡研究了鹽漬土的鹽脹特性。張強等[6]利用小波神經網絡建立了秸稈灰混凝土強度預測模型。王彥虎[7]、霍珍生[8]等利用BP神經網絡建立了碳酸鹽漬土的凍脹模型，并利用該模型對影響凍脹的因素進行敏感性分析。劉宇峰[9]則分別利用BP神經網絡、自適應模糊神經推理系統和支持向量機建立了鹽漬土未凍水含量的預測模型。展超[10]基于BP神經網絡建立了適用于富水砂層地區渣土改良試驗的效果預測模型，用于土的坍落度、滲透系數和內摩擦角的預測，效果良好。這些已有研究表明這些神經網絡模型均能較好地反映出影響因素與預測目標之間復雜的關系，可靠性比較高。

目前，國內學者對鹽漬土的研究主要是針對氯鹽和硫酸鹽，對于宏觀影響因素影響下改良碳酸鹽漬土單軸壓縮強度的神經網絡模型研究尚比較缺乏，因此，本文采用實驗室配制碳酸鹽漬土的方式，考慮了固化劑摻量、溫度和加載速率對改良鹽漬土的無側限抗壓強度的影響，通過室內無側限抗壓試驗獲得了土樣的強度值。最后，利用BP神經網絡建立了固化碳酸鹽漬土無側限抗壓強度的預測模型。

1 研究方法

1.1 樣本數據收集和預處理

試驗用土來自黑龍江省哈爾濱市機場路第2通道的粉質黏土。室內進行試驗前，在試驗土樣中加入1.5%的碳酸氫鈉固體顆粒，配制成人工鹽漬土。改良鹽漬土的無側限壓縮試驗考慮石灰和粉煤灰摻量、溫度和加載速率3個因素的影響。其中，石灰和粉煤灰總摻量保持15%不變，設計4組摻量組合：3%石灰+12%粉煤灰、5%石灰+10%粉煤灰、6%石灰+9%粉煤灰、7%石灰+8%粉煤灰；試驗溫度設置4組：0 ℃、-5 ℃、-10 ℃、-15 ℃；加載速率設置3組：0.5 mm/min、1 mm/min和2 mm/min。

試驗前，將試樣在標準養護室養護28 d，然后將4組溫度的樣品放入凍箱中冷凍24 h。試樣的無側限抗壓強度采用WDW-100微機控制電子萬能試驗機測定。

1.2 模型結構及樣本數據預處理

各因素與固化土無側限抗壓強度之間的關系難以用精確的數學模型來表達，而BP人工神經網絡具有很強的自學習和自適應能力，能很好地反映出這種復雜的非線性關系。因此，本文用Python語言編寫了BP人工神經網絡，嘗試建立二灰固化土的無側限抗壓強度預測模型。BP神經網絡一般包括輸入層、隱含層和輸出層，采用誤差反向傳播學習算法，其學習過程主要包括正向傳播和反向傳播兩部分，在正向傳播中，輸入信息從輸入層經過權值的處理傳到隱含層，在隱含層經過激活函數處理傳向輸出層，最終輸出預測值。

首先需要確定BP神經網絡各層的層數。本文確定神經網絡的結構為三層，包括一個輸入層、一個隱含層和一個輸出層。在本次改良土的無側限壓縮試驗中，考慮了改良鹽漬土的固化劑摻量、溫度、加載速率作為影響土樣強度大小的主要因素，因此選擇這3個因素的數據導入模型中，對這三種因素的改良鹽漬土強度預測。神經網絡的結構，如圖1。

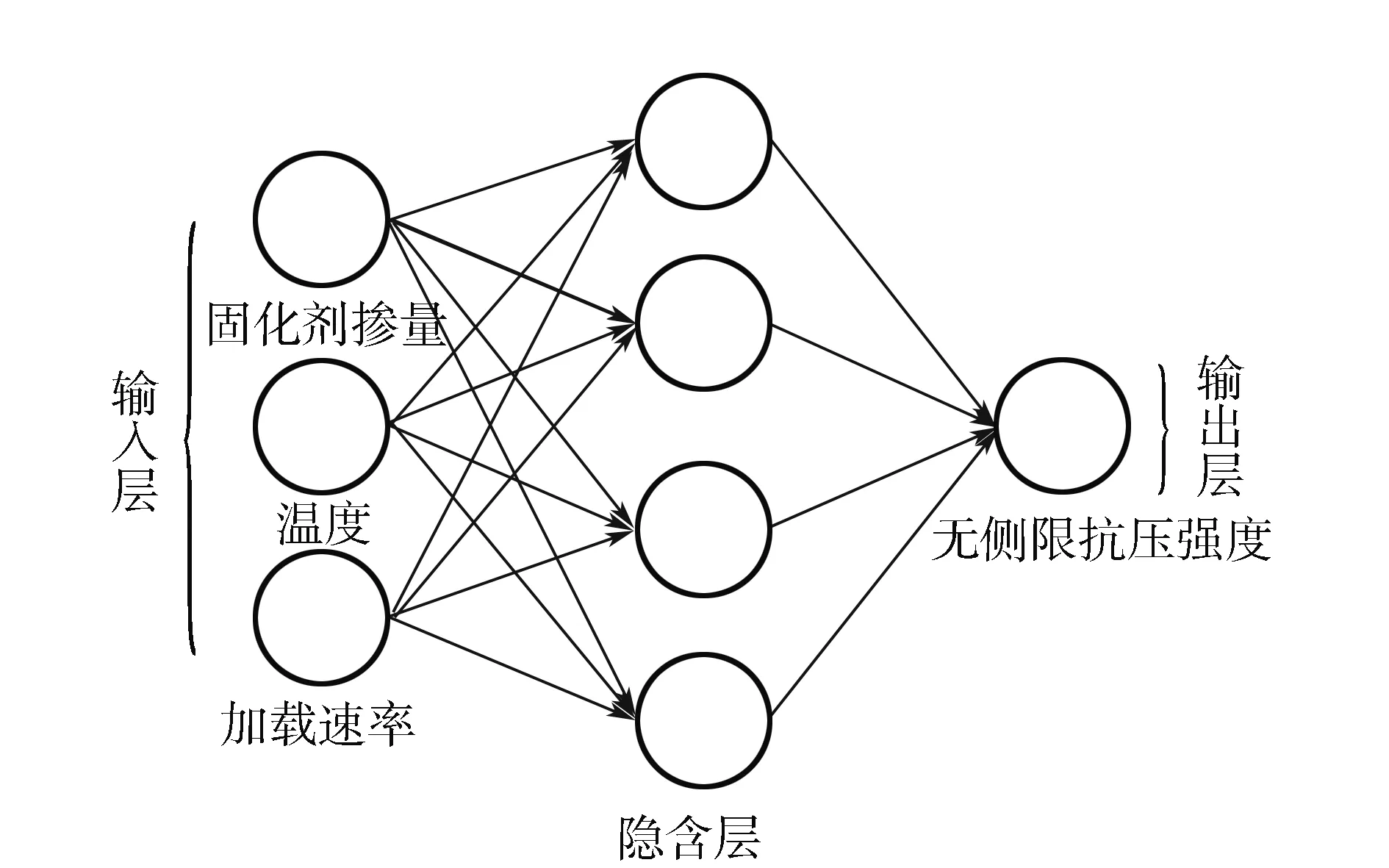
圖1 BP神經網絡的拓撲結構

為提高和保證預測精度，使模型訓練的樣本數據要有較好的代表性，在開始訓練預測模型之前，要對無側限抗壓強度值及各影響因素數據進行標準化處理。本文從48個樣本數據中隨機選取40個作為訓練樣本，剩下的8個作為預測樣本。將所有的數據參數X按公式(1)進行歸一化處理。

(1)

式中：Xmin是參數X中的最小值；Xmax是參數X中的最大值；Xn是參數X歸一化后的值。

2 基于BP神經網絡強度預測模型的建立

2.1 模型結構參數選取

神輸入層3個節點，分別為固化劑摻量(本文用石灰摻量代替固化劑摻量參與模型計算)，溫度和加載速率；隱含層節點數待定；輸出層1個節點為無側限抗壓強度。每層的輸入數據通過上一層的輸出數據經sigmoid函數獲得。

根據式(2)可確定[11]隱含層節點的數量范圍為2～12。

(2)

式中：n是隱含層的神經元個數；ni是輸入層的神經元個數；n0是輸出層的神經元個數；a是一個0～10之間的固定值。

用訓練樣本對不同隱含層節點的模型進行訓練，可得到不同隱含層節點模型訓練后結果的均方根誤差(RMSE)和確定系數(R2)，如圖2所示。從圖中可以看出，當隱含層的神經元個數n=11時，數據訓練后RMSE達到最小值，且R2達到最大值，所以本次隱含層神經元個數設置為11。

經過計算統計，本次神經網絡模型的參數值選擇如下：輸入層神經元個數為3；隱含層=1；

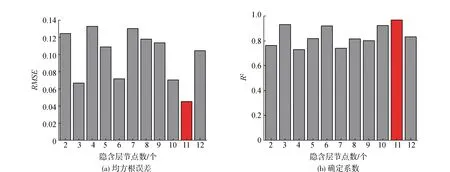
圖2 不同隱含層節點模型訓練后結果

隱含層神經元個數=11；輸出層個數=1；模擬精度=0.001；學習步數=10 000；學習算法為梯度下降法。

2.2 訓練模型誤差分析

當隱含層節點數為11時，無側限抗壓強度訓練值和實測值如圖3所示。由圖知，訓練值和實測值趨勢基本相同，誤差最小為0.0009，可以反映三因素對改良土無側限抗壓強度的影響；其中訓練樣本編號為3、28、35、39的誤差較大，而這些誤差均發生在試驗設置的邊界條件下，即固化劑摻量為7%(石灰)、溫度為0 ℃或-15 ℃、加載速率為0.5 mm/min或2 mm/min的條件下，模型的訓練誤差較大，主要原因是模型收斂過程中為保持連續性，變化幅度較大處誤差變大，這說明還有其他因素影響改良土無側限抗壓強度。

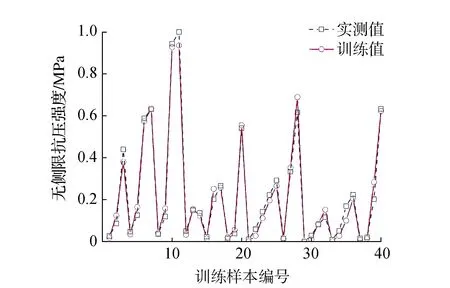
圖3 模型訓練值和實測值對比

2.3 模型預測結果分析

將選中的預測樣本歸一化后輸入到建立好的模型中進行預測。無側限抗壓強度預測值和實測值的對比如圖4所示。由圖4可以看出，兩條曲線基本重合，說明模型預測基本準確。最小誤差為0.0003，最大誤差為0.0599，所有預測結果誤差均小于0.1；且均方根誤差為0.0270，確定系數為0.985，說明模型基本能反映改良土的無側限抗壓強度變化趨勢，也能很好地預測無側限抗壓強度值。

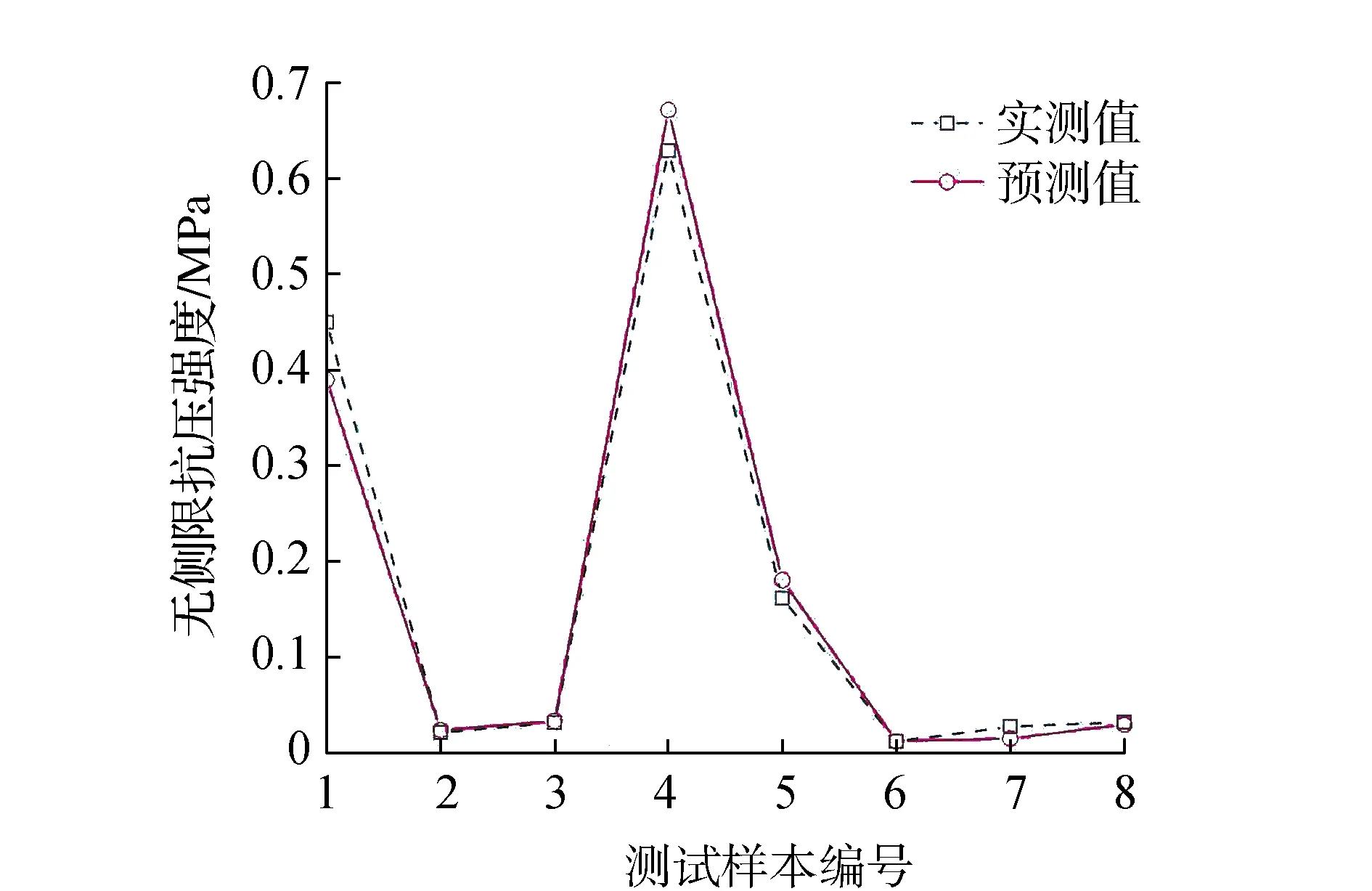
圖4 模型預測值和實測值對比

3 結 論

本文通過BP神經網絡建立了改良鹽漬土的無側限抗壓強度預測模型，研究結論如下：

(1)無側限抗壓試驗選擇3個影響因素：固化劑摻量、溫度和加載速率。影響因素作為輸入層，改良土的無側限抗壓強度作為輸出層，建立了BP神經網絡無側限抗壓強度預測模型。

(2)從無側限抗壓試驗獲得的48個樣本數據中隨機選取40個作為訓練樣本，剩下的8個作為預測樣本。當隱含層的神經元個數n=11時，數據訓練后RMSE達到最小值，且R2達到最大值，說明此時模型收斂精度最高，所以本次隱含層神經元個數設置為11。

(3)訓練模型在試驗設置的邊界條件處為保持收斂，會有較大的誤差，但總體訓練值與實測值誤差不大，可以反映出各影響因素對改良土無側限抗壓強度的影響趨勢。

(4)預測值和實驗值的最小誤差為0.0003，最大誤差為0.0599，所有預測結果誤差均小于0.1；且均方根誤差為0.0270，確定系數為0.985，說明該強度預測模型預測效果較好，能很好地反映改良土的無側限抗壓強度變化趨勢。