立足課堂 滲透極限思想

張 麗

(江蘇省揚州市高郵市龍虬鎮張軒小學 225604)

數學課堂教學固然應該教會學生許多必要的數學知識，但讓學生在學習這些結論的過程中掌握數學思想方法才是更為重要的.隨著對數學思想的關注度越來越高，數形結合、分類思想、轉化與化歸思想、模型思想、方程思想等數學思想應用頻率越來越高，數學思想方法已經受到越來越多的教師的重視.然而，在一些小學的數學課堂上，由于很多教師對極限思想的價值認識不足，缺少滲透極限思想的教學設計，數學極限意識的培養痕跡淡薄.

如何在小學生的頭腦中播種下極限思想的“種子”，讓其生根、發芽，為今后長成數學知識的大樹打下堅實的基礎，筆者認為必須以課堂教學為主線，瞄準數學極限思想展開課堂教學活動，并且向課外延伸.下面，筆者根據自己所在的鄉村學校特點，以課堂教學為背景，談一談在小學數學課堂中滲透極限思想的幾點策略.

一、建立無限觀念

首先，什么是“極限”?簡單地說，就是一個變化著的量，在其變化過程中無限趨近于一個固定的數值，我們就把這個固定的數值稱為變化的量在其變化過程中的極限.極限是用以描述變化的量在一定的變化過程中的終極狀態的概念.

極限的含義中有兩個關鍵詞:一是無限量，二是固定值.因此，要讓學生接受極限思想，首先要幫助學生建立無限的觀念.

1.在數與代數中建立無限觀念

在學習四年級下冊億以上數的認識時，學生認識了億，教師出示數位表后提問“”

追問：為什么億級前面還有省略？

生：還有比億位大的數.

師：億已經特別大了，還會有比它大的數？我們來做一個游戲，請一位同學先寫一個較大的數，下一個同學要寫一個比他大的數，看看能不能找出最大的自然數.

通過游戲，讓學生明白：億雖然是一個很大數，但它仍然是有限的，比億更大的數有很多，你想象有多大就有多大.自然數從0開始，后面的數總比前面的數多1，一個一個地數，總也數不完，因此說“自然數的個數是無限的，沒有最大的自然數”.這樣，在數的認識中初步建立起無限的觀念.

在除法的教學中，除了讓學生充分理解算理，掌握算法外，還可以有機地引導學生體會有限與無限的思想.兩個數相除，如果不能得到整數商，所得的商會有兩種情況.一種情況是商的小數的位數是有限的；另一種情況，我們要提供感性材料，讓學生多算幾步，充分感知“除不盡”的新情況.然后引導學生仔細觀察小數部分數字排列的規律，得到:商從某位起出現一個數字或幾個數字依次不斷重復出現.“不斷重復出現”表示什么意思?由此引出循環小數的概念.以前學生對小數概念的認識僅限于有限小數，學習了循環小數以后，小數概念的內涵進一步擴展了，循環小數就是一種無限小數，讓學生體會到了無限的思想.

在我們教材中，還有許多知識涉及數量無限多的情況，如:年月日的認識、 小數的意義、分數的意義、因數與倍數等知識中都蘊含著無限思想的影子.

2.在認識圖形的教學中建立無限的觀念.

在認識圖形時也可以滲透有限與無限的思想.例如在教學線段、直線、射線的認識時，讓學生聯系實際，充分體驗，建立對線段、直線、射線的一影象.

如何用有限長度的線段表示無限長度的直線，是學習的一個難點.在學生了解了線段、射線、直線的概念后，讓學生在作業本上畫出線段，再讓他們把線段的一端往前不斷延伸，直觀感受無限的“概念”.

但是在實際生活中學生很難找到直線的具體實例.射線和直線都是為了深人研究，在頭腦中想象出來的一種“線”.讓我們閉上眼睛-起想象一下射線，一條線段向一端無限延長，延長，再延長……一直不斷延長下去.那直線呢，繼續想象一條線段向兩端無限延長，延長，再延長……一直不斷延長下去.我們需要讓學生合理想象，感悟極限，調動多感官參與“無限”的感知中.

在《角的認識》學習中，體會角的兩邊延伸的特性，通過學習直線的位置關系，感知平行線也、是一種無限的量，體會無限.在教學過程中，我們要充分利用好教材，在傳授探索新知的過程中，潤物細無聲的滲透無限概念.

二、感悟極限思想

極限的概念很抽象，要通過具體的案例，在應用極限思想解決某些“無限”問題的過程中來感悟極限思想.

1.在新知學習中感悟極限思想

在《圓的面積》一課教學中，筆者沒有選用書中將圓轉化為平行四邊形的方法，而是讓學生追尋古人的足跡進行摸索.讓學生不斷對折手中的圓紙片，隨著折疊的次數越多，圓被等分的份數也越多，學生發現所得到的圖形越接近于三角形，啟發學生可以把圓等分成若干個三角形來計算面積.

同時，在多媒體出示魏晉時代的數學家劉微在其《九章算術注》中應用“割圓術”得到圓的半周長與半徑之積等于圓的面積，劉微在描述這種作法時說“制之彌細，所失彌少，制之又制，以至不可制，則與圓周合體而無所失奧”.讓學生了解極限思想的產生和應用，可追溯到古代.

接著讓學生利用割圓術推導圓的面積公式，先從圓的內接正六邊形面積算起，接著研究正八邊形面積，正十邊形面積，正十二邊形面積，多媒體展示正多邊形的邊數越來越多，正多邊形就越來越接近圓.

現代多媒體手段能很好的化抽象為直觀，幫助學生理解數學思想與方法.圓的面積是學生第一次接觸曲線圖形的面積，如何讓學生感悟和體會“化曲為直”和“極限”的數學思想呢?教師設計了跟隨古人的足跡，結合現代化的教學手段，出示圓內接正六邊形，接著是正八邊形，隨著電腦展示多邊形的邊數越多這個正多邊形就越接近圓，最后把幾種正多邊形進行對比，對比之后，教師引導學生討論:是什么原因使最后的正多邊形最像圓呢?讓學生在觀察、想象中感悟“化曲為直”和“極限”的數學思想，課后讓學生思考是否還有別的推導方法，讓學生利用課堂所學極限思想，把圓剪拼成長方形，推導公式.

在小學階段如圓的面積、圓柱的體積等公式的推導過程都體現了化曲為直、化圓為方的極限思想，在通過有限分割拼合的變化趨勢，想象它們無限分割的最終結果，既讓學生掌握了計算公式又萌發了無限逼近的極限思想.由于受年齡特征的制約，小學生對極限思想不會有深刻的理解，但這并不等于我們教師在小學數學教學中可以淡化對極限思想的滲透，相反應該抓住一切可以利用的契機加以滲透，為他們形成數學思想提高抽象思維能力以至將來學習極限知識奠定基礎.

2.在練習中感悟極限思想

六年級下冊《數的認識》總復習中有一到題目：

在括號里填適當的數.

(1)0.9，0.99,0.999，( ),( )……

上面兩組數分別會越來越接近幾?

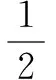
極限思想的滲透是一個螺旋式的上升的過程，作為教師，我們應當有足夠的耐心和信心，立足課堂，有選擇地、有針對性地、適時地對學生進行極限思想的滲透，為其今后學習高等數學播種下希望之芽.