基于參數周期李亞普諾夫方程的閉環系統設計

謝琪龍，陳揚陽，鄧小龍，劉敏綺，劉祎妮

（1.廣西師范大學數學與統計學院，廣西 桂林 541006；2.廣西師范大學計算機科學與信息工程學院/軟件學院，廣西 桂林 541006）

0 引言

由Clohessy以及Witshire給出的C-W方程是一個線性時不變方程，在以往研究圓軌上的航天器軌道交會優化控制問題上都取得了較理想的效果。但是以往的研究在基于C-W方程進行航天器軌道交會優化控制設計時，沒有考慮現實中進行反饋控制器的參數浮動以及攝動力的存在而引起的參數變化或參數增益。然而在實際操作中，不能包容控制器微小的參數變化的閉環系統必然是不穩定的，而且很有可能是致命的。故本文設計了有界線性時變連續周期閉環系統。使得系統兼備魯棒性及優良的性能，使得航天器更加核心競爭力[1]。

1 線性有界時變連續周期閉環系統的設計

1.1 相關研究綜述

Wada, Asai和Ikeda建立了利用Riccati型微分方程的解設計LTV控制器和LTI系統的非指數鎮定，以此來提高控制性能。Cacace, Germani和 Manes 采用了時滯相關時變觀測器增益來實現期望的指數誤差衰減。指數時間增益用于Ahmed-Ali, Fridman, Giri, Burlion和Lamnabhi-Lagarrigue對樣本數據的穩定和估計進行了研究，發現與常數增益相比，最大采樣間隔可以相差很大，許多非線性或非完整的機械系統，如普通輪式移動機器人不能通過使用光滑pure-state（純態）反饋控制來確定。但是其仍然可以通過使用光滑時變反饋來保持穩定性。

周彬博士研究設計的線性時變閉環系統能夠實現在有限時間內收斂的研究方法（BinZhou,Finite-time stabilization of linear systems by bounded linear time-varying feedback）對此我們在此基礎上進行進一步的改進，將周期這一個重要性質考慮進去，得到一個新的、基于周期李亞普諾夫穩定性理論的線性時變周期閉環系統。

本文通過建立線性有界時變連續周期反饋來實現有限時間內的鎮定。在不考慮外部干擾情況下，允許設計一個時變參數存在于反饋增益中，求解參數李亞普諾夫方程來實現控制器的設計。所有設計均有賴于參數李亞普諾夫方程的主要特征，該解對應參數李亞普諾夫方程的一個參數的導數的上界和下界。

據參數李亞普諾夫方程的特性，實現閉環系統收斂速度快于指數，或者調節時間小于正無窮，此時的線性控制器是穩定的（或漸進穩定的）。并有反饋增益k是時變的，控制u(t)在收斂期間保持有界。基于此原理，設計一個收斂速度快于指數且調節時間小于正無窮的有界線性時變連續周期反饋系統。

本文考慮航天器姿態定向保持并姿態鎮定，考慮目標航天器在偏向率較小的低地球軌道運動，并且目標航天器與追蹤航天器相距不遠（≤50km）的交會情況。

我們考慮一個非線性相對運動模型：

其中，旋轉目標航天器的軌道旋轉坐標系統如圖一所示：

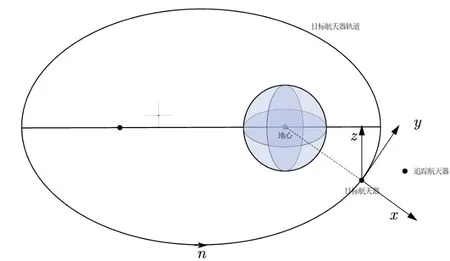
圖1 旋轉目標航天器的軌道旋轉坐標系

其中，坐標原點為目標航天器的質心，x-軸在從地心到目標航天器的質心的直線上，y-軸在沿著目標航天器軌道的切線方向上，z-軸與x-軸、y-軸構成右手系。 并且坐標系以地球的質心為圓心，R為軌道半徑，n為軌道角速度進行周期旋轉。

本文考慮航天器姿態定向保持并姿態鎮定，考慮目標航天器在偏向率較小的低地球軌道運動，并且目標航天器與追蹤航天器相距不遠（≤50km）的交會情況。

對于上面的航天器交會模型，我們可以得到以下的非線性相對運動模型：

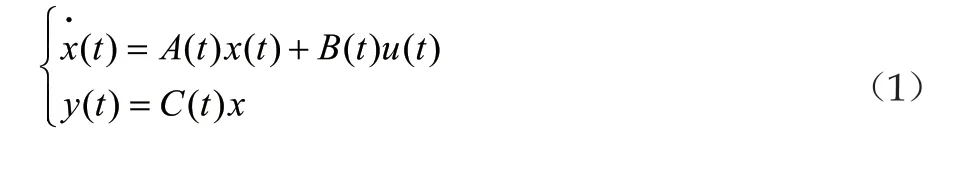
首先考慮預控制器u(t)，對其進行參數化反饋，有

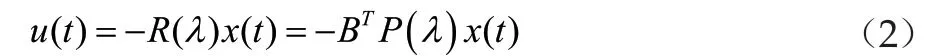
將閉環系統收斂參數λ設為隨著時間變化的，是一個關于時間t的函數。即λ表示閉環系統的收斂速度，而且我們有P(λ)為參數李亞普諾夫方程的一個矩陣解。

若參數李亞普諾夫方程考慮應用在周期控制系統的設計上，由周彬博士研究論文[2](具有飽和非線性的控制系統研究的參數Lyapunov方法及其應用)可得參數周期方程對于參數周期李亞普諾夫方程，存在一個P(λ)為其通解。假設P(λ)>0，則系統（1）以及預控制器（2）組成的閉環系統軌跡上的時間導數滿足以下方程

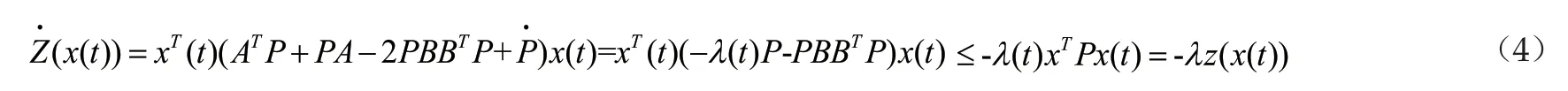
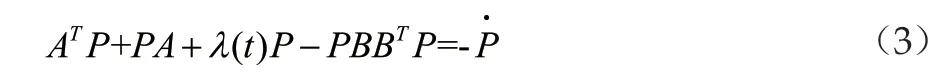
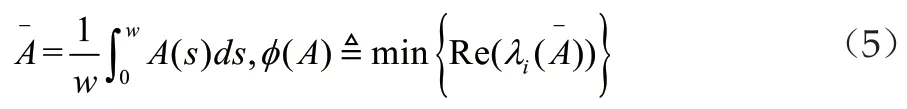
下面我們將需要證明我們的參數解P(λ)是滿足如下的一個形式的一個矩陣，從而知道該解是合適的。

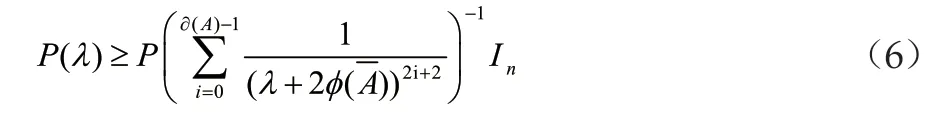
1.2 狀態反饋

考慮設計時變反饋系統，以預控制器（2）的反向增益形式，實現收斂速度比指數快的收斂。首先選擇一個類參數李亞普諾夫方程的函數，設計一個λ(t)，使得x(t)在在有限時間內收斂于零；與此同時，保證預控制器u(t)在收斂過程中有界。

（1）閉環收斂速度參數λ(t)的尋找。對于上文中所要求設計的時間T，我們可以將其表示為如下形式

其中我們對其中的參數進行定義

通過以上的定義，可以知道時間T是小于一個周期w的，即

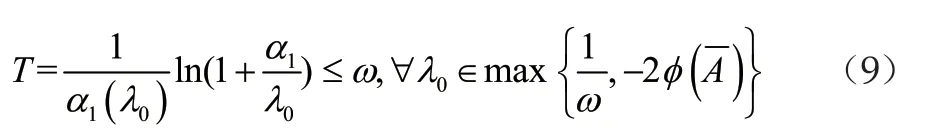
給定關于λ的一個合理解集，通過給出該解集，我們對λ的取值進行限定

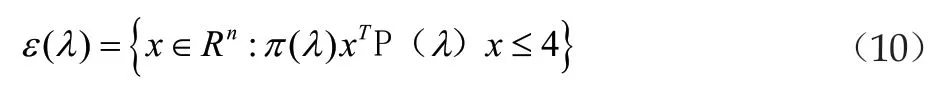
考慮下面的有界線性時變狀態反饋

利用該狀態反饋，我們可以得到一個形如方程（5）的一個證明，其中σ是一個常數。

對于參數周期李雅普諾夫方程（3）的一個參數解λ，給出如下的形式：

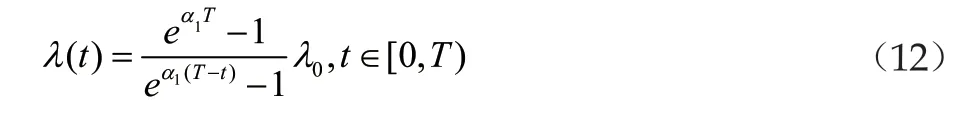
通過驗證可以知道它是滿足一個微分方程的解的形式

系統參數滿足以下不等式關系：

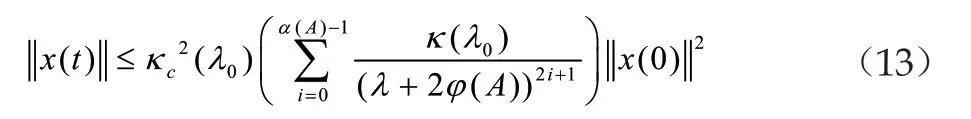
即ε(λ)包含在閉環系統里，其中是一個關于的一個函數表達式。由預控制器（2）和系統（1）組成的閉環系統使得包含在閉環系統的引力域內。

（2）預控制器u(t)在收斂過程中有界。在實際進行航天器控制中，u(t)應存在一個控制上界。考慮在設計軌道控制器的時候，設計控制器使之可容許控制輸入盡可能的小。使得系統（1）在較小的控制輸入下，其狀態可逼近原點。

考慮基于觀測輸出反饋情況，設計一個可觀測的控制器，其形式如下

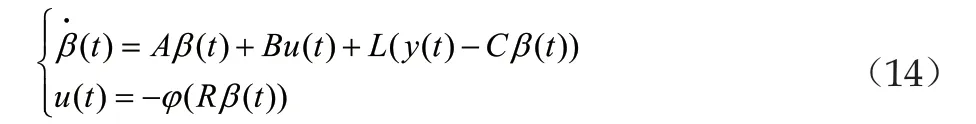
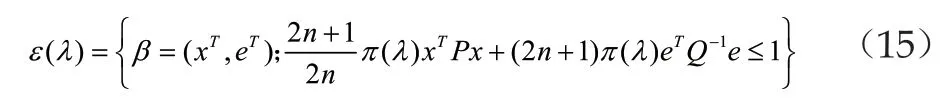
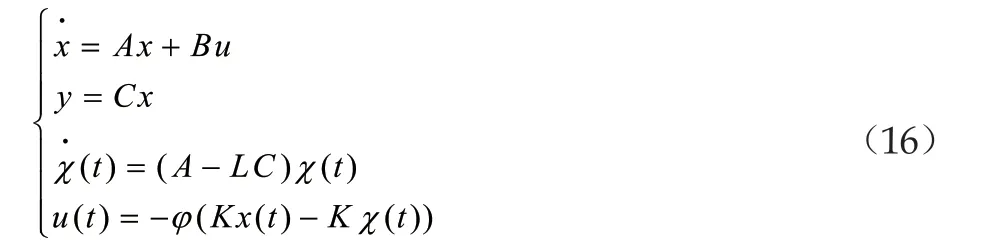
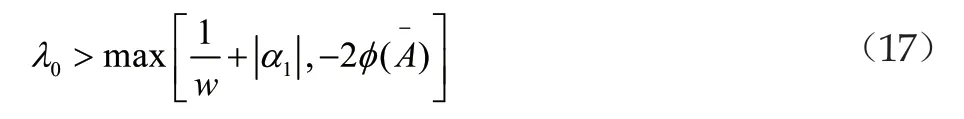
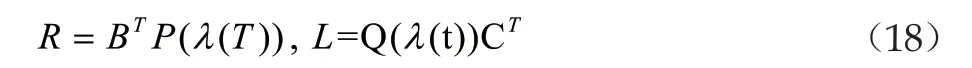
其中，T為給定的有限常數，并且我們通過重新設計T，可以得到T的一個如下表達形式：

T的取值此時應該與系統的一些初始參數相關，它與參數λ0、α1不再滿足一定的指數關系，而是滿足一個對數關系表達式[4]。此時，相應地可以得到閉環系統的收斂參數λ滿足如下形式

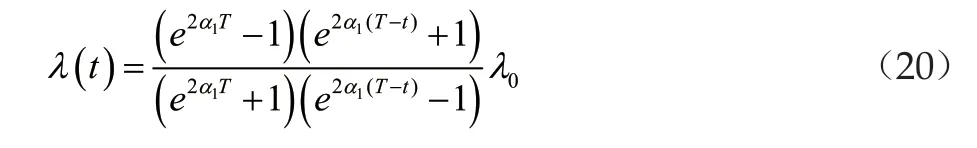
從而可以得到收斂參數λ是滿足等式

并且可以知道它是快于指數收斂的。通過相應的驗算可以由李亞普諾夫方程的穩定性理論得到，由系統（1）和基于觀測的反饋控制器（2）組成的閉環系統（14）是漸進穩定的。

2 結語

本文基于C-W方程的航天器交會的非線性相對運動模型，依據參數李亞普諾夫方程及其穩定性理論，通過對其解及其性質進行研究，得到了由航天器系統和預控制器組成的閉環系統。并根據參數李雅普諾夫方程的穩定性理論結合周期理論建立相關的類參數里亞普諾夫方程，并以此作為核心依據，進行航天器閉環系統預控制器的設計。通過一些向量標量的手段，能夠很好的證明所設計的系統是穩定的而且是合理的，能夠滿足所有的穩定性要求。通過對參數周期李亞普諾夫方程性質的研究，能夠證明閉環系統狀態，即其參數可以在有限時間內實現漸進收斂，并且設計的系統是由系統參數和初始條件所決定的。

自此我們得到了所求的控制系統，并證明所給系統的穩健性。本文所提出的閉環設計方法可以應用在航天器軌道交會控制系統中。應用此方法進行航天器系統的設計可以使得該航天器的閉環系統具有魯棒性。