基于模糊數學的高維稀疏數據聚類統計方法設計
周燕茹
(巢湖學院 數學與統計學院,安徽 巢湖 238000)
隨著數據庫管理系統的應用范圍越來越廣,企業或其他機構均積攢了海量數據[1].對數據實施聚類統計處理能夠判斷數據間的相似度,從而獲取重要的數據特征信息.然而,數據維度與稀疏度成反比,數據對象會分布于各個維度子空間內,傳統的聚類方法在這方面的聚類效果較差,原因是距離函數容易無效、算法復雜度高與聚類中心選擇過于隨機等[2-3].且傳統的數據分析工具僅具備查詢與統計等作用,難以高效聚類高維稀疏數據.
一直以來,高維稀疏數據聚類統計方法始終是數據挖掘方面的一大難題[4].邵俊健[5]等人針對高維數據聚類效果較差問題,設計了一種具有抗噪性能適用高維數據的增量式聚類統計方法,提升其抗噪性能與聚類效果;武森[6]等人針對數據對象易于劃分至更大類內問題,設計了一種基于拓展差異度的高維數據聚類統計方法,有效縮短聚類時間.然而在實際應用中發現,隨著現階段數據量及其復雜度的提高,上述兩種方法在聚類統計稀疏度較低的數據集時效果仍然較差.
模糊數學是一種分析模糊性情況的數學方法,主要用于模糊聚類分析與模糊綜合評判等.其中,最為常用的是模糊C均值算法(Fuzzy C-means,FCM).為此,本研究以FCM算法為基礎,設計了基于模糊數學的高維稀疏數據聚類統計方法,以期提升聚類統計效果.
1 高維稀疏數據聚類統計方法設計
1.1 FCM算法
FCM算法是模糊數學的分支,該算法以模糊思想表示對象和簇間的關系.對象y對于集合A的模糊隸屬度函數是hA(y),hA(y)∈[0,1],在數據聚類過程中,將聚類獲取的簇當作模糊集合,FCM算法目標函數的表達公式如下:
(1)
其中,聚類中心編號為i;數據點編號為j;模糊組的聚類中心為ci;hij∈[0,1];加權指數為m∈(1,∞);i與j之間的歐幾里德距離為dij=‖yj-ci‖2.
FCM算法的具體處理步驟如下:
步驟1:獲取聚類數量c(2≤c≤n),樣本數量為n,確定m(2≤m≤∞)的值;初始化隸屬矩陣H得到H(T),將T作為迭代的標記.初始化需要符合的要求如下:
(2)
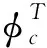
(3)
(4)
其中,聚類中心編號是k.
步驟4:對比分析每次優化后隸屬矩陣的差距,若‖H(T+1)-H(T)‖<εT,那么完成聚類統計,隸屬矩陣差距的標準數值是εr;若‖H(T+1)-H(T)‖>εT,設置T=T+1,返回至步驟2.
1.2 改進的模糊聚類算法與聚類統計方法設計
1.2.1 優化初始聚類中心
為避免陷入局部最優,在FCM算法運算過程中,需要反復初始化聚類中心,延長聚類統計時間.為解決這一問題,本研究利用特殊的初始聚類中心選取方法,獲取數據集凸包邊界中的初始聚類中心,確保各聚類中心距離較遠,避免出現局部最小值的情況.具體步驟如下:
步驟1:求解數據集的平均值,將與該值距離最遠的數據點當成首簇聚類中心;
步驟2:計算首簇聚類中心與全部數據點間的距離;
步驟3:按照貪心選擇策略選取首簇聚類中心以及平均值較遠的數據點,將其當成第二簇聚類中心,直到得到k簇聚類中心為止;
步驟4:以平均值為目標,令全部聚類中心向其移動,移動間距為兩者距離的10%,提升聚類的收斂速度[7].
1.2.2 類間中心點影響
由于FCM算法并未分析各類別數據簇中心點間的彼此排斥影響,導致該算法難以對高維稀疏數據實施聚類,通過添加權重機制[8]改進FCM算法,使其適用于高維稀疏數據的聚類統計.將已知類與未知類均添加至FCM的目標函數內,變更后的目標函數為:
(5)
其中,未知類內第i簇聚類中心為Pi;已知類內第k簇聚類中心為Rk;權重為wj;第j個數據點包含在i內的程度為αij;j包含在k內的程度為βkj;聚類中心數量為l.α與β需符合的條件如下:
(6)
通過拉格朗日乘子法計算:
(7)
其中,拉格朗日乘法算子為λ.
計算G(H,T,P,λ)內變量Pi的偏導,過程如下:
(8)
根據公式(8)可得到:
(9)
依據同樣方法求解G(H,T,P,λ)內變量αij與βkj的偏導,公式如下:
(10)
(11)
其中,簇的編號分別為a與b.
通過引入權重機制提升FCM算法中各類簇的聚類中心競爭剩余數據點間重疊范圍內的特征空間.通過加權指數m決定簇心間的排斥力,該值與排斥力成正比[9].
1.2.3 優化余弦距離
雖然FCM算法具備較優的聚類低維數據集性能,但在聚類高維稀疏數據時,其效果不佳[10].由余弦距離替換FCM算法中的歐幾里德距離,計算公式如下:
(12)
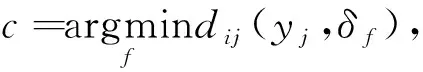
(13)
根據公式(13)可得到:
(14)
在每個數據塊很小(對象很少)的情況下,為各簇劃分的對象數量同樣較少[11],說明χc也較小.針對各簇僅存在一個對象的現象,獲取:
(15)
其中,高維稀疏數據向量為yj,該向量中僅包含非常少的非零元素.這就說明yj和剩余數據間常用詞的數量明顯低于各數據內存在的詞數量[12].通過二進制方法加權內yj的詞,若yj內存在單詞,那么yji=1;若yj內不存在單詞,那么xji=0,針對這一情況可獲取:
(16)
得到:
(17)
在高維稀疏數據內數據塊不大的情況下,通過‖φc‖2確定d(xj,φc).同時,由于‖φc‖2的值與yj沒有關系,為避免全部對象劃分到和聚類中心存在最小歐幾里德距離的相同簇內,在各次迭代結束時[13],需標準化處理聚類中心,公式如下:
(18)
標準化處理聚類中心時,對象與聚類中心的距離通過公式(12)右側的最后一項確定,它屬于yj與φc間的內積,確保FCM算法中的h存在意義,針對FCM算法存在:
(19)
更改上述公式獲取:
(20)
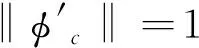
(21)
為解決模糊聚類內yj在全部簇內的隸屬度非常接近問題,需要歸一化處理各目標矢量[15],使其變成單位范數‖yj‖=1.歐幾里德距離公式變更為:
(22)
在yj歸一化成單位長度的情況下,FCM算法的全部迭代過程中,優化完成的聚類中心歸一化已改為基于余弦距離的FCM算法.基于此,以余弦距離替換原有的歐幾里德距離,提高高維稀疏數據聚類統計效果.由此,通過優化模糊數學中的FCM算法實現了對高維稀疏數據的聚類統計.
2 實驗與分析
2.1 實驗設置
為驗證上述設計的基于模糊數學的高維稀疏數據聚類統計方法的實際應用性能,設計如下實驗.將文獻[5]中的具有抗噪性能適用高維數據的增量式聚類統計方法(方法1)和文獻[6]中的基于拓展差異度的高維數據聚類統計方法(方法2)作為對比,要個具體點的方向本文方法共同完成性能驗證.
將HR(Hit-rate,命中率)與ARI(Adjusted Rand Index,調整蘭德指數)作為衡量3種方法聚類統計性能的指標,HR的取值范圍是[0,0.3],ARI的取值范圍是[0,1],兩者的取值均與聚類效果成正比.其中,HR的取值高于0.2則代表該方法具備較優的聚類效果,ARI的取值高于0.5則代表該方法具備較優的聚類效果.
在某網絡中隨機選取6個真實數據集作為實驗對象,數據集的具體信息如表1所示.
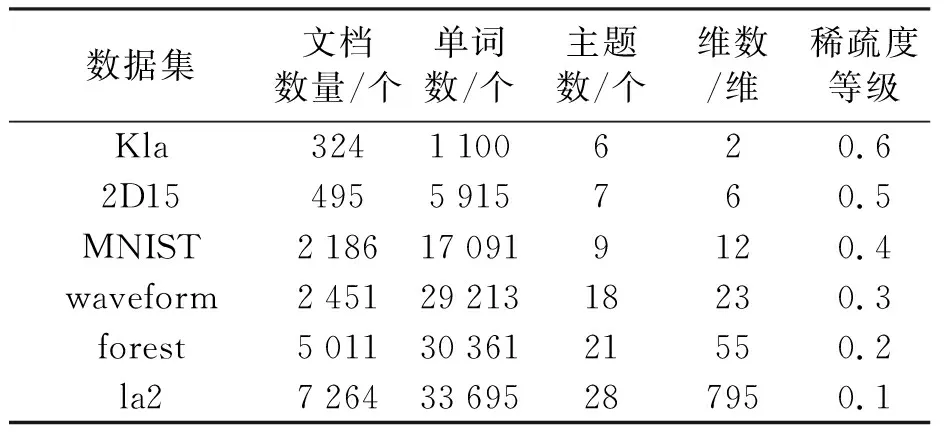
表1 數據集的具體信息
2.2 性能分析
為確保3種方法具備可比性,在隨機分塊完成時,每次使用3種方法過程中所利用的隨機分塊需要具備一致性.利用3種方法聚類統計上述數據集,測試3種方法在數據總量不同分塊時的ARI值,測試結果如表2所示.
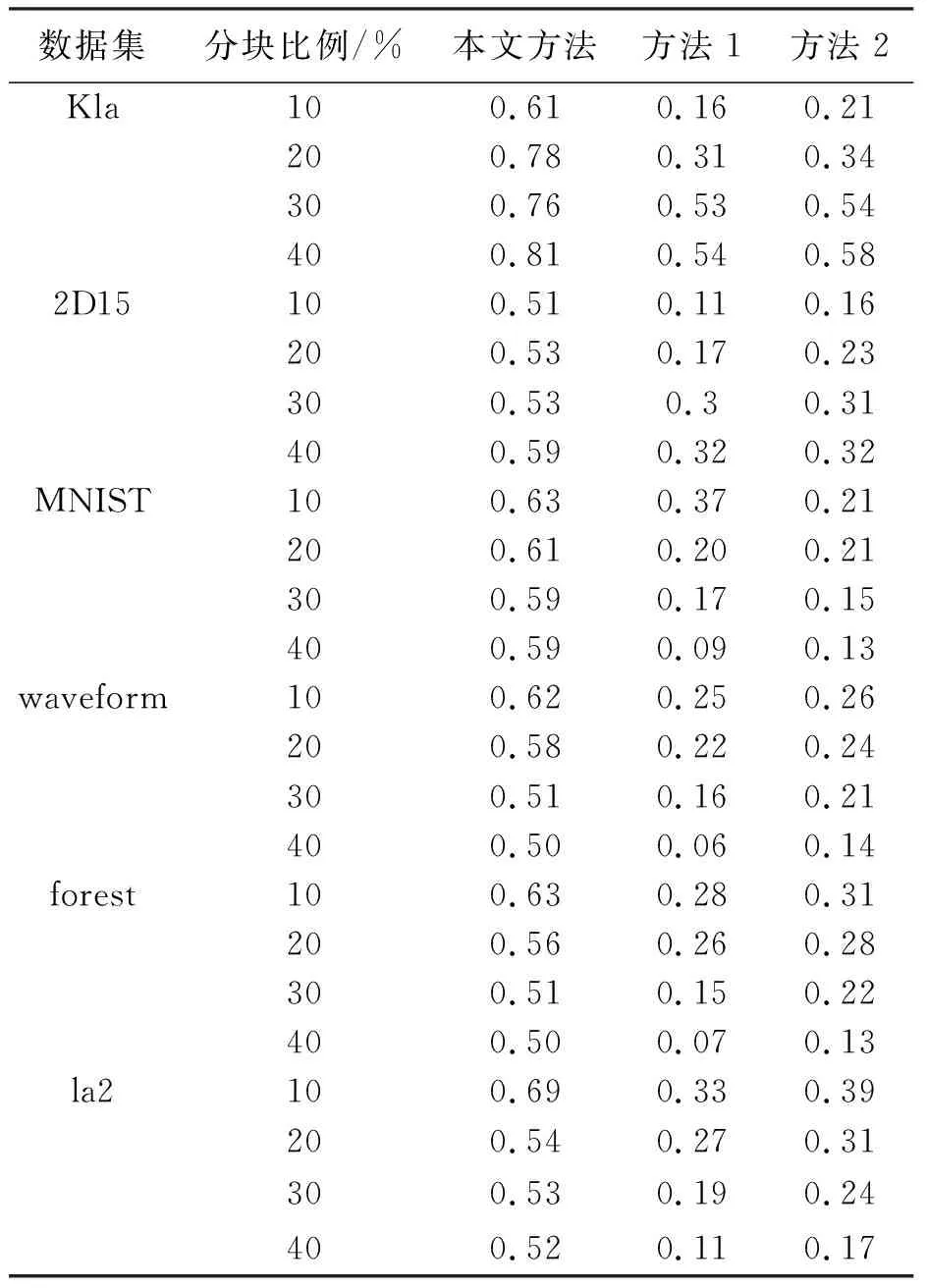
表2 3種方法在不同分塊時的ARI值
當數據集維度較小時,3種方法分塊數量越大,ARI值越大,聚類統計效果越好;當數據集維度較大時,3種方法的分塊數量越小,ARI值越大,聚類統計效果越好.合理劃分分塊大小,可提升3種方法的聚類效果.根據表2可知,當數據集維度以及分塊比例不同時,本文方法的ARI值明顯高于另外兩種方法,本文方法的ARI值波動范圍是0.50至0.81,方法1的ARI值波動范圍是0.06至0.54,方法2的ARI值波動范圍是0.13至0.58.上述實驗證明:本文方法在不同數據集維度及分塊比例時的ARI值最高,且最低ARI值也高于標準值0.5,聚類統計效果較優.
測試3種方法在聚類統計不同稀疏度等級的數據集時的HR值及執行時間,測試結果如圖1與表3所示.

稀疏度等級圖1 HR值測試結果
數據集稀疏度等級越低代表其越稀疏.由圖1可知,隨著稀疏度等級的逐漸提升,3種方法的HR值均有所增長,在不同稀疏度等級時本文方法的HR值均最高、變化幅度最小,且最低HR值也在0.2之上,其余兩種方法僅有在稀疏度等級為0.6時其HR值才超過0.2.上述實驗證明:在聚類統計不同稀疏度等級的數據集時,本文方法的HR值最高,且受稀疏度影響較小.
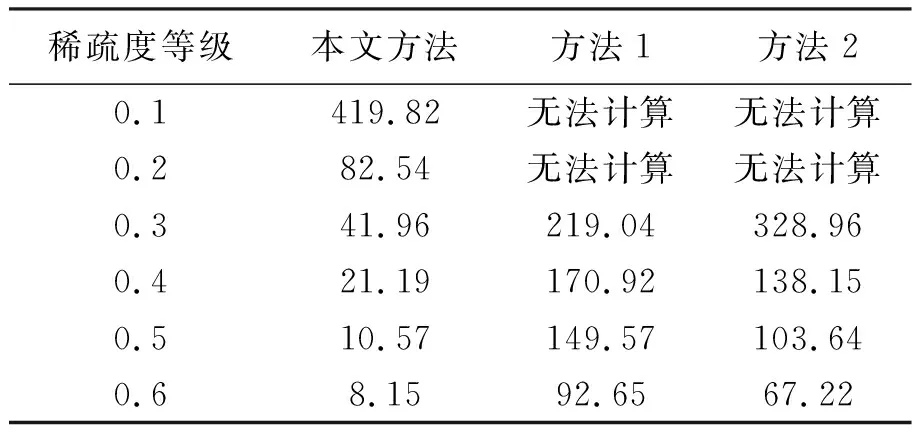
表3 聚類統計執行時間(μs)
根據表3可知,在數據集稀疏度等級較低時,方法1與方法2無法完成聚類統計.隨著稀疏度等級逐漸提升,3種方法的聚類統計執行時間逐漸縮短,本文方法的執行時間最少.上述實驗證明:本文方法適用于稀疏度較低的數據聚類統計,且聚類統計效率較高.
3 結 論
設計了基于模糊數學的高維稀疏數據聚類統計方法,以FCM算法為基礎,在此基礎上加以改進,解決局部最優問題,合理劃分數據集的分塊比例,從而提升了聚類統計效果,也降低了數據集稀疏度等級對聚類統計效果的影響,提升了聚類統計效率.

