衛星網絡中基于時變圖的節能資源分配策略*

帥家成，劉雨,2**，望育梅,2

（1.北京郵電大學人工智能學院，北京 100876；2.鵬城實驗室網絡與通信研究中心，廣東 深圳 518000）

0 引言

衛星網絡由于其覆蓋范圍廣、不受地理因素影響等特點，被廣泛用于自然災害的檢測、災害損失評估等多種地球觀測任務。由于衛星網絡的高動態性、鏈路的不連續性與高時延等特征，其資源的時變表示是當前研究難點之一[1-2]。此外，由于衛星節點能量主要由太陽能電池板提供，所以衛星在太陽光被遮擋時無法獲得能量，這就導致能量同樣成為衛星網絡路由的稀缺資源[3]。文獻[4] 用時變圖（TEG,Time-Expanded Graph）來表示衛星網絡的時變拓撲并研究了當衛星節點資源受限時網絡中的資源分配問題，解決了當網絡中節點資源受限時的最大流問題，但并沒有考慮能量消耗。文獻[5]、文獻[6] 討論了衛星網絡中的資源分配策略，但沒有降低網絡中的能量消耗。文獻[7] 提出了一種從用戶行為分析的角度研究了數據中繼衛星（DRS,Data Relay Satellite）系統中的資源分配問題，然而仍沒有將傳輸能耗作為優化指標。文獻[8]、文獻[9] 提出了基于時變圖的低能耗路由算法，但會降低網絡的吞吐量性能。

為了解決觀測任務中資源分配的傳輸能耗問題，本文提出了一種貪心迭代式算法，來對觀測任務中的能耗進行優化，同時保證網絡吞吐量不減少。首先，為了表示網絡動態變化的拓撲，采用了時變圖[10]來表示網絡中的連接情況、能耗水平等，在時間與空間兩個維度上的關系。由于衛星節點的資源受限，當一顆衛星的傳輸資源小于能與其建立連接的鏈路容量之和時，需要進行傳輸資源的分配。本文在時變圖中添加了虛擬節點來表示受限的衛星傳輸資源，并添加了虛擬起點、虛擬終點與虛擬邊來簡化問題。此外，能耗水平被添加至圖中構成資源能耗時變圖（RCTEG,Resource-Cost Time-Expanded Graph）。基于RCTEG，將本文提出的算法與文獻[4] 中的Ford-Fulkerson 算法和文獻[11] 中 的Boykov-Kolmogorov 算法進行了對比，驗證了本文提出算法在減少能耗的同時不損耗網絡吞吐量。

1 系統模型

1.1 任務模型

假設在網絡中存在R顆衛星，一個地面目標S，一個地面站D。R顆衛星中存在R1顆遙感衛星與R2顆中繼衛星。遙感衛星從地面目標S獲取數據后，如果存在連接，其可以選擇直接將數據傳至地面站D，也可以選擇將數據傳至中繼衛星，最終將數據傳至地面站，中繼衛星只能從遙感衛星獲取數據，無法直接從地面目標獲取數據，其任務過程如圖1 所示。由于衛星節點的資源受限，在衛星可同時與多個節點建立連接且無法同時以所有鏈路的最大容量進行傳輸時，需要進行傳輸資源的分配，以使網絡能耗減小的同時不以犧牲吞吐量為代價。設需要進行資源分配的衛星節點數目為R3。

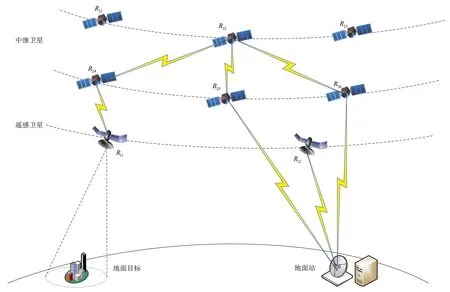
圖1 地球觀測任務

1.2 能耗模型

衛星網絡中，星間鏈路的傳輸會受到衰減，其中最主要的是自由空間傳播衰減。衛星的接收功率PR由式(1)決定[12]：

式中，PT為發射功率，GT為發射天線增益，GT為接收天線增益，LP為自由空間傳播衰減，LP由式(2) 決定：

式中d為傳播距離，λ為工作波長，c為光速，f為工作頻率。假設星間與星地通信的工作頻率相同，接收與發射增益相同，則當接收功率相同時，衛星節點的發射功率僅與兩點的傳輸距離相關，假設傳輸時間t相同，則衛星節點的傳輸能耗e僅與傳輸節點之間的距離相關，如式(3) 所示，式中k可以看作一個常數。

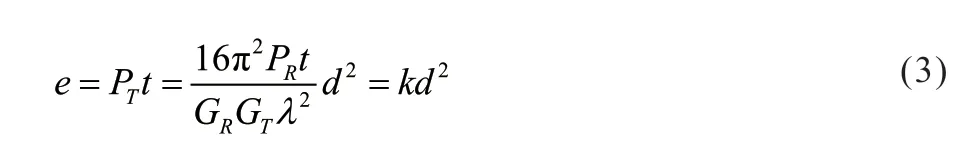
由于衛星節點的高度移動性，兩節點之間在連接窗口內的距離不斷變化，將單次連接窗口內的衛星傳輸能耗視為由兩節點之間的平均距離決定。由于無需研究衛星傳輸的具體能量，將能耗進行了歸一化，將平均距離為6 300 km 的衛星傳輸能耗設為1。通過式(3)得到其他鏈路的傳輸能耗水平。

1.3 資源能耗時變圖

為了表示網絡中傳輸資源，能耗在時間與空間上的關系，本文將傳輸能耗的概念引入TEG[10]，得到RCTEG。在RCTEG 中，時間T被分為h個時隙T=｛t1,t2,……,th｝，每個時隙的長度為Δτ，每個時隙內的拓撲是固定不變的。RCTEG 由節點集V、鏈路集A、容量集C與能耗集E構成，RCTEG={(V,A,C,E)}。

節點集V包括：源點集VS={Si|1≤i≤h}表示h個時隙內的地面目標；遙感衛星節點集1≤l≤R1}表示h個時隙內的遙感衛星；中繼衛星節點集表示h個時隙內的中繼衛星；終點集VD={Di|1≤i≤h}表示h個時隙內的地面站；虛擬節點集表示h個時隙內需要進行資源分配的衛星節點對應的虛擬節點。此外，節點集還包括虛擬起點Sv與虛擬終點Dv，通過虛擬起點與終點可以使網絡的多源多匯問題轉化為單源單匯問題。

鏈路集A包括：傳輸鏈路集1≤i≤h,v∈V-VD,v∈V-VS-VR3}表示在同一時隙內的星間鏈路或星地鏈路；存儲鏈路集表示同個實體節點在不同時隙間的存儲能力；虛擬鏈路集表示需要進行資源分配的節點與其虛擬節點之間的連接；輔助鏈路集Aa={(Sv,Si),(Di,Dv)|1≤i≤h}表示虛擬起點、虛擬終點與起點和終點之間的連接。

由TEG（圖2（a））改造后的RCTEG={(V,A,C,E)}如圖2（b）所示。圖中，Sv為虛擬起點，S1與S2為前兩個時隙內的地面目標，A1與A2分別同時與兩個節點存在連接，且這兩個鏈路的容量之和比A1與A2的傳輸資源大，A1與A2無法同時滿足兩個鏈路的最大容量傳輸，所以需要進行傳輸資源的分配。而B1、B2、C1與C2的傳輸資源等于與其連接的鏈路容量，所以無需建立虛擬節點。為A1與A2的虛擬節點，用來表示兩節點資源的受限。D1與D2為前兩個時隙內的地面終點站，Dv則為虛擬終點。在RCTEG 中，除虛擬節點外，所有節點都與其在其他時隙的對應節點由存儲鏈路相連。構造RCTEG 的關鍵為，得到需要進行資源分配的節點添加虛擬節點集VR3和通過節點之間的距離從而得到其能耗集E。

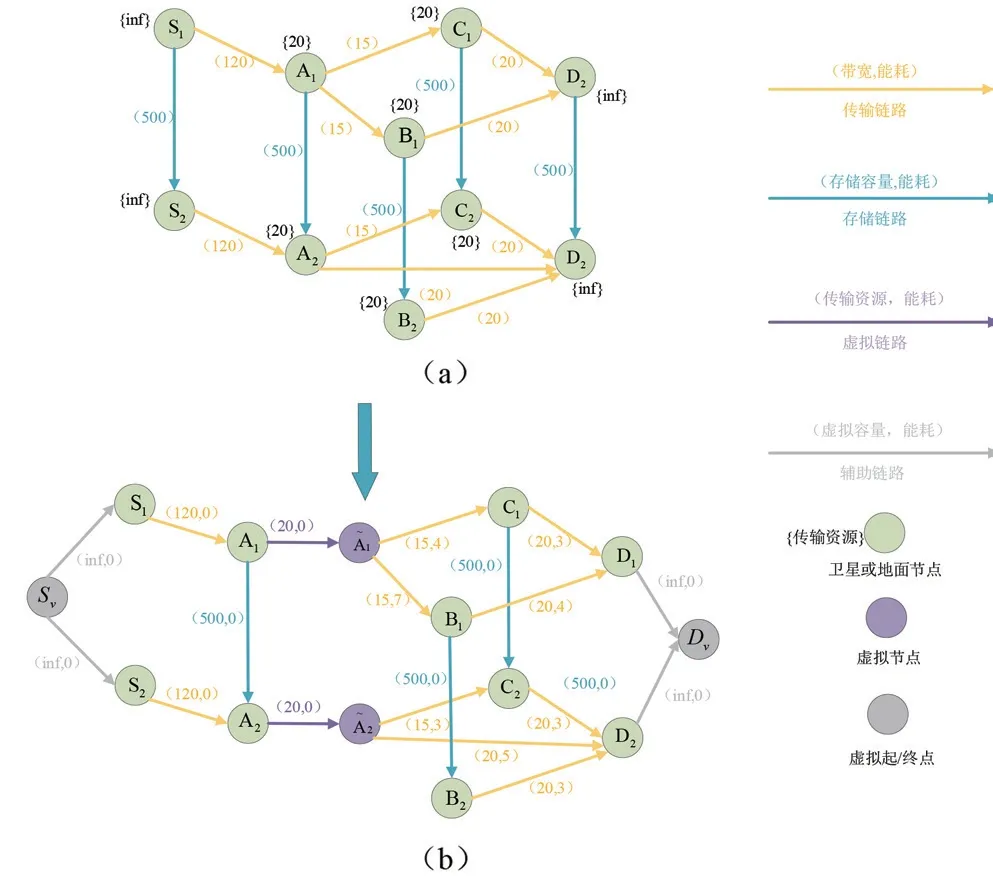
圖2 兩個時隙內的RCTEG

2 基于RCTEG的節能資源分配算法

2.1 問題模型

本文需要解決的問題是尋找一種使網絡流量達到最大同時能耗較低的傳輸資源分配方案。在時間T內，問題可被描述為：

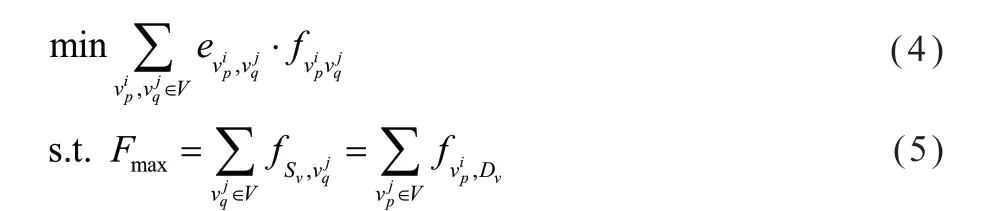
流守恒限制：流入節點與流出節點的流量相等。

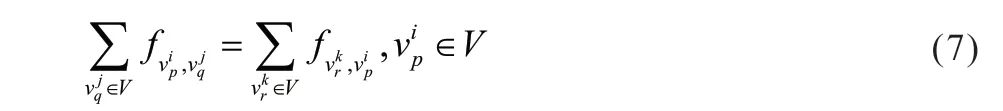
在滿足容量限制與流守恒限制的條件下，本文問題的優化目標為在不損耗網絡流量的同時降低能量消耗。

2.2 基于RCTEG的節能資源分配算法

基于RCTEG，本文提出了一種貪心的迭代尋找網絡中最小能耗資源分配方案的流擴充算法（EERA,Energy Efficient Resource Allocation），在不損耗網絡吞吐量的同時，盡可能地減少網絡的總能耗。此算法在搜尋路徑時總是優先尋找能耗較小的路徑并將節點的資源分配到此路徑內，從而得到能耗較小的分配方案。

算法步驟如下。

首先，根據網絡的連通情況找到需要進行資源分配的節點并構造虛擬節點集VR2，此后，根據節點之間的距離獲得鏈路的能耗集E，構造出當前網絡的RCTEG。

第二步，在圖中，根據能耗集E找到網絡中從虛擬起點Sv到虛擬終點Dv的一條最小能耗路徑Pmin_cost，作為一條可擴充流路徑。

第三步，根據容量集C沿此條路徑尋找各個鏈路的可擴充流量，選擇各個鏈路中可擴充流量的最小值作為該路徑的可擴充流Δfp進行流的擴充，得到fp并更新容量集C。

此后，經過流擴充之后，進行能耗集E的重構，在E中為有流流過但未達到鏈路最大容量的邊添加反向邊能耗，達到鏈路容量的邊則只存在反向邊能耗。

最后，回到第二步，直到無法找到圖中從虛擬起點Sv到虛擬終點Dv的一條最小能耗路徑時，算法結束，并得到網絡的節能最大流量資源分配方案。

以圖2 中的兩個時隙內網絡拓撲為例，圖3 為EERA算法與Ford-Fulkerson 算法的分配方案對比。圖中綠色邊表示有流經過，綠色數字表示經過流的大小，紅色邊與紅色數字表示EERA 算法的不同資源分配選擇。

Ford-Fulkerson 算法得到的分配方案中（圖3（a）），鏈路中流過的流量為5，鏈路中流過的流量為15，而EERA 算法得到的分配方案中（圖3（b）），鏈路中流過的流量為15，鏈路中流過的流量為5。Ford-Fulkerson 算法與EERA 算法得到的網絡流量同為40，但EERA 算法網絡的總能耗為255，而Ford-Fulkerson 算法所得到的網絡能耗為300。

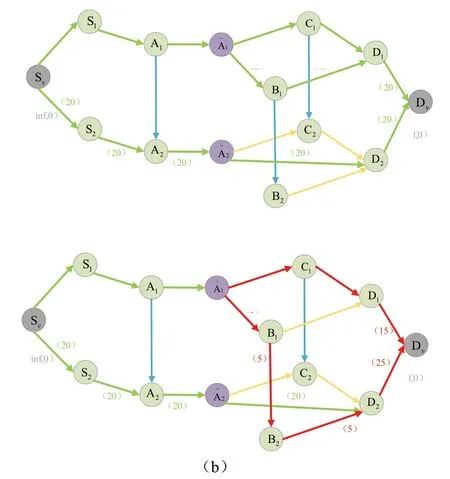
圖3 EERA算法與Ford-Fulkerson算法的資源分配對比

3 仿真實驗

利用STK（Satellite Tool Kit，衛星工具包），可以獲得衛星網絡的連通情況與網絡各節點的距離，通過計算平均距離可得到衛星鏈路的歸一化能耗。在仿真中，本文在兩個不同的網絡中對算法的性能進行了驗證。

兩種網絡場景下的地面目標均為羅馬，地面站均為北京，仿真時間兩個小時。遙感衛星的數目設置為2，位于太陽同步軌道，高度為631 km，傾角為97.9°。中繼衛星軌道高度為1 414 km，傾角為52°。遙感衛星從地面獲取數據的速率設置均為120 Mbit/s，星間鏈路容量設置為20 Mbit/s，星地鏈路容量設置為30 Mbit/s。第一種網絡下中繼衛星為(12/6/4)Walker 星座，共12 顆衛星，第二種網絡下中繼衛星為(18/6/4)Walker 星座，共18 顆衛星。

在每種網絡場景中，分別進行了兩組實驗，第一組實驗中將存儲能力設置為5 000 MB。傳輸資源在10～50 Mbit/s 之間變化。第二組實驗中，傳輸資源設置為30 Mbit/s，存儲能力在3 500～6 500 MB 之間變化。對比算法采用了文獻[4]中采用的Ford-Fulkerson算法與Boykov-Kolmogorov算法[11]。

網絡中存在12 顆中繼衛星時，三種算法的能耗、吞吐量隨傳輸資源變化而變化的對比如圖4。由圖4 可見，三種算法在不同傳輸資源下的吞吐量相同，而本文提出的EERA 算法的網絡總能耗小于其他兩種算法。網絡中存在18 顆中繼衛星時的三種算法的性能對比如圖5。同樣地，三種算法的吞吐量相同，而EERA 算法的能耗要明顯小于其他兩種算法。且在相對復雜的網絡中，EERA 的節能效果較明顯。

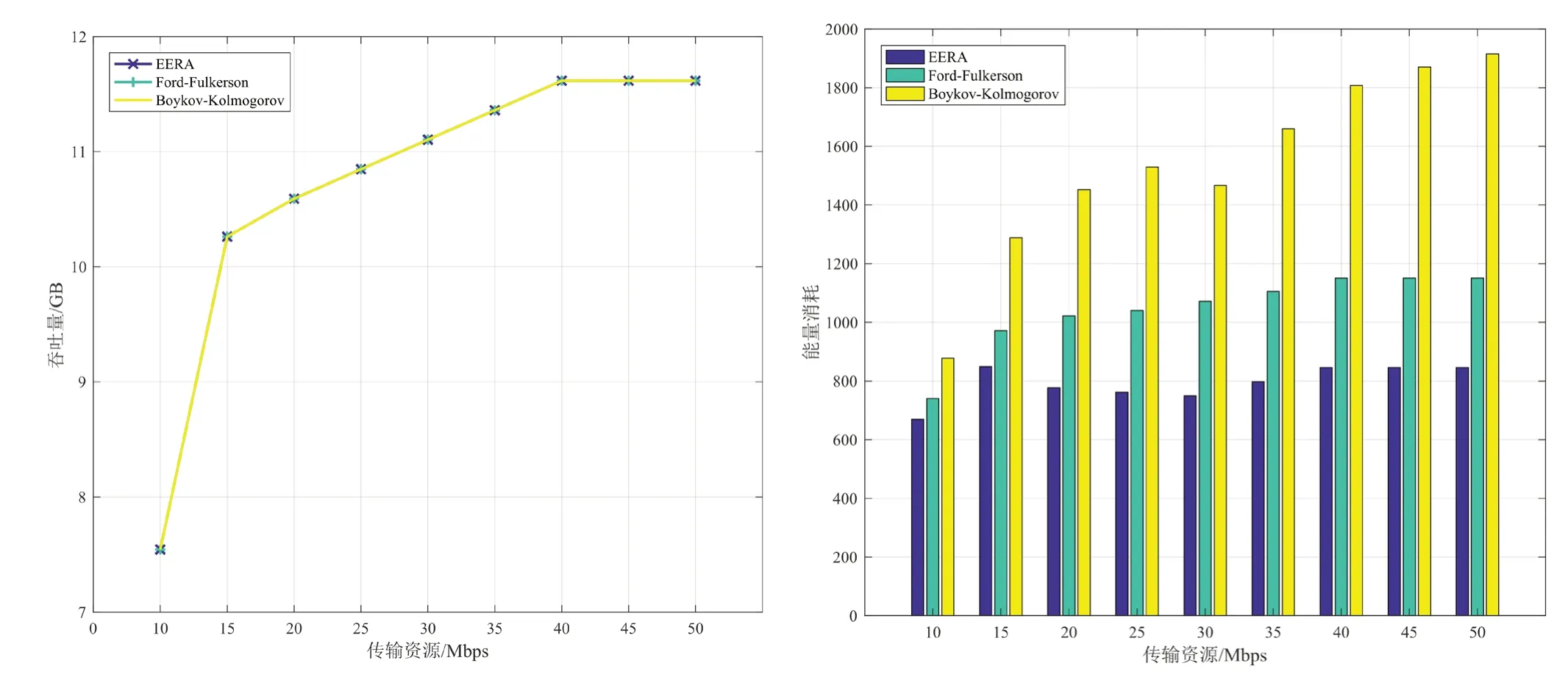
圖4 12顆中繼衛星時三種算法性能隨傳輸資源變化的對比

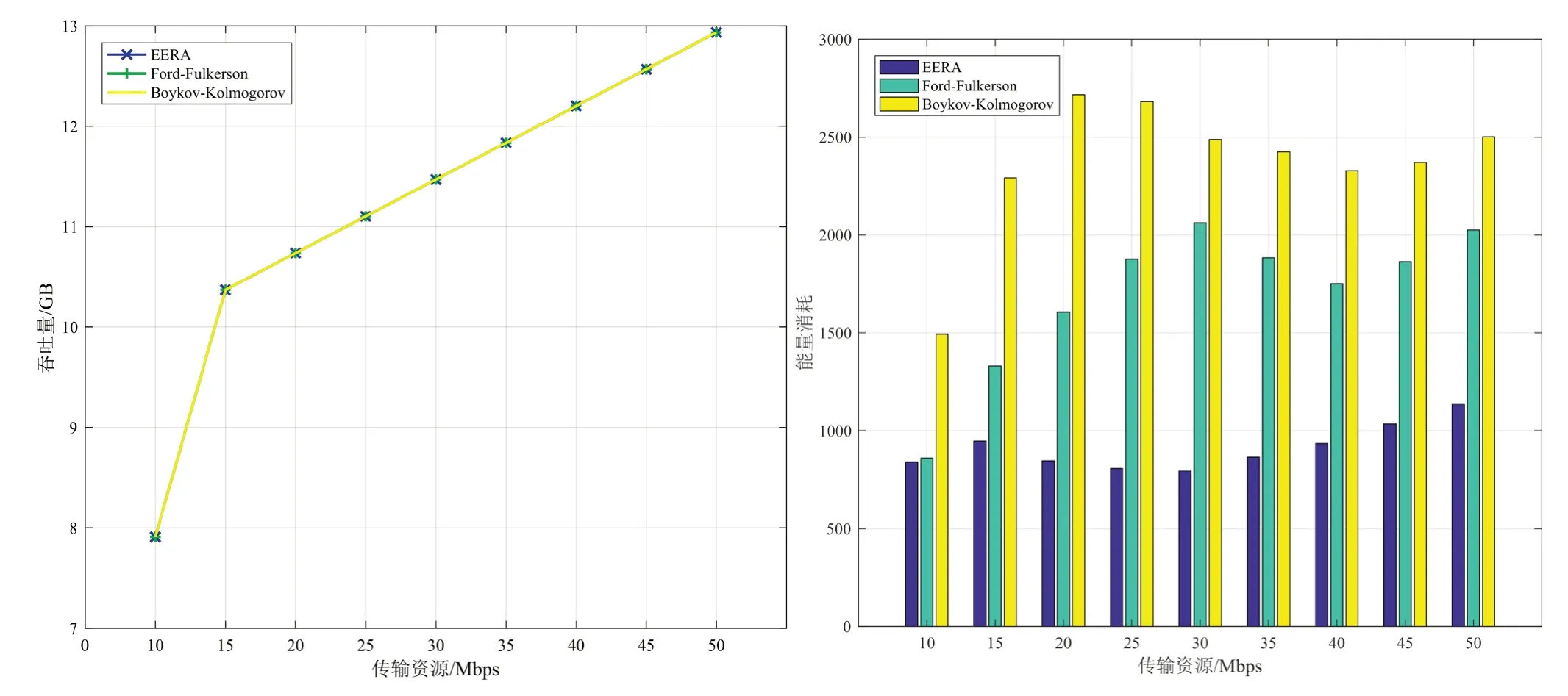
圖5 18顆中繼衛星時三種算法性能隨傳輸資源變化的對比

第一種網絡下，三種算法的能耗與吞吐量隨衛星節點的存儲能力變化的對比如圖6 所示。同樣可以看出，存儲能力變化的同時，三種算法的吞吐量相同，而EERA算法的能耗要小于其他兩種算法。第二種網絡下的三種算法隨存儲能力變化的性能對比如圖7。同樣地，EERA算法與其他兩種最大流算法得到的吞吐量相同而能耗要少于另外兩種算法。且在較為復雜的第二種網絡中，其能量消耗的減少較為明顯。

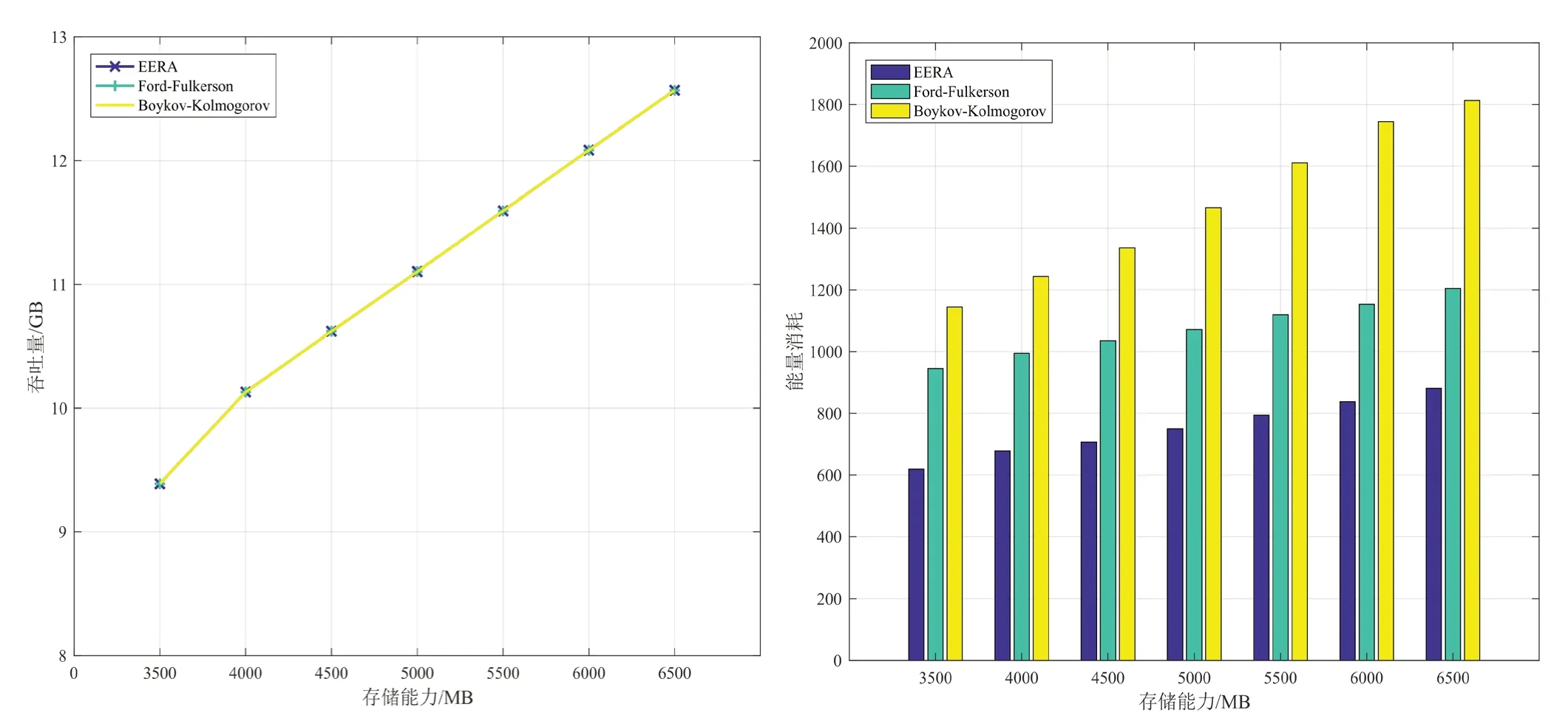
圖6 12顆中繼衛星時三種算法性能隨存儲能力變化的對比

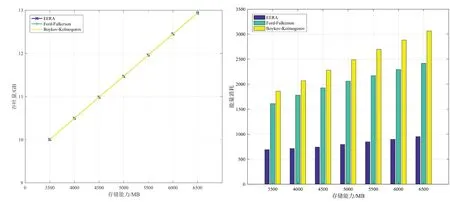
圖7 18顆中繼衛星時三種算法性能隨傳輸能力變化的對比

4 結束語

本文考慮了衛星網絡中地球觀測任務中，在衛星節點傳輸資源受限情況下的傳輸資源分配問題。基于時變圖，提出了一種貪心的迭代尋找網絡中最小能耗資源分配方案的流擴充算法EERA，此算法可以在不損耗網絡吞吐量的條件下降低網絡能耗。通過與當前已有研究的對比得到，此算法可有效降低能耗并不已犧牲吞吐量為代價。此外，算法在較復雜網絡中的效果更優。下一步將考慮地面網絡與更復雜的衛星星座融合的低能耗資源分配策略。