固有應變法在鋼板三角感應加熱變形計算中的應用

張雪彪，鹿想，劉海涵

(大連理工大學 a.運載工程與力學學部船舶工程學院；b.工業裝備結構分析國家重點實驗室，遼寧 大連 116024)

在船廠，帆形板的水火彎板成形多采用三角加熱工藝，即火炬在靠近板邊時進行擺動加熱，從而增大板邊的加熱面積和溫度，以得到大的板邊收縮量，達到帆形板的成型要求。對于感應熱源的水火彎板工藝，見圖1，當感應器在板邊處進行擺動加熱時，也可以獲得同樣的收邊加熱效果。

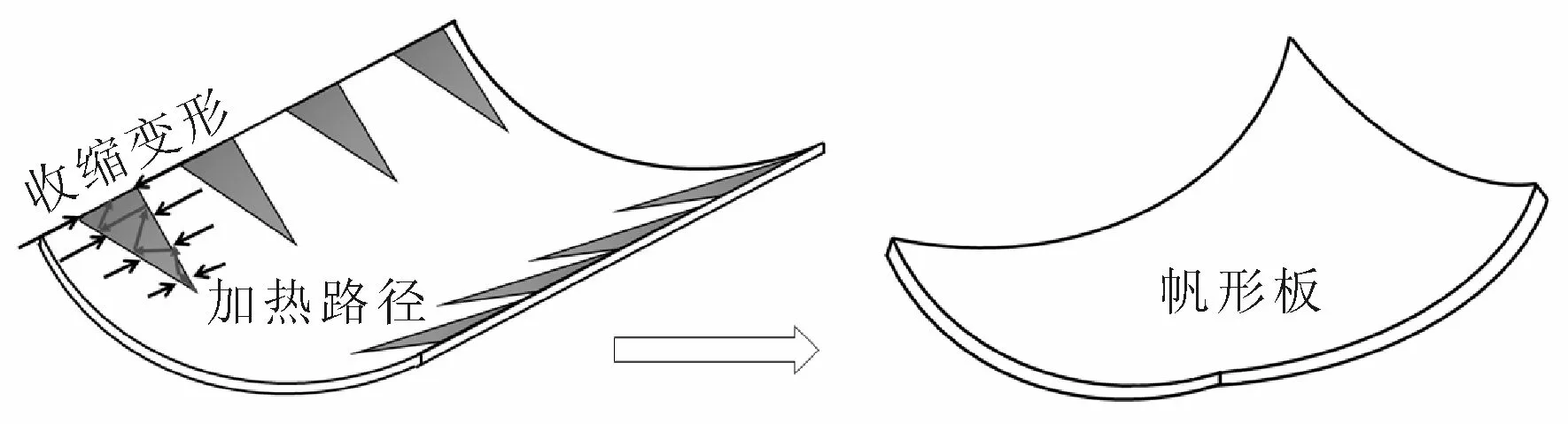
圖1 帆形板變形過程

對于鋼板多加熱線的變形計算問題，采用電磁-熱-結構耦合的有限元模型進行計算是困難的，因為模型復雜，計算量巨大，所以研究者多采用基于固有應變法的彈性有限元模型進行計算。有學者等使用圓盤-彈簧模型作為三角加熱過程的簡化熱彈塑性力學模型，在三角加熱的固有應變區域內進行分區域的等效載荷加載[1]。有學者提出計算三角加熱形狀和位置的算法，建立加熱形狀和殘余變形的函數關系。相關的研究均采用火焰熱源的圓盤-彈簧模型來計算固有應變，力學模型不適用于除圓形外的其他感應器形狀，也不能簡單地應用于鋼板感應加熱工藝。為此，考慮采用鋼板電磁-熱耦合的熱彈塑性模型得到加熱線附近的塑性應變值，然后對塑性應變進行積分，從而獲得固有應變沿加熱線的分布規律，在進行彈性有限元分析時考慮固有應變的分布規律，使之符合鋼板三角感應加熱的變形特點。

1 加熱實驗與數值模擬

針對鋼板的三角感應加熱工藝，文獻[3]在大量實驗的基礎上確定了三角感應加熱的擺動加熱路徑，并建立了基于輥彎板的鋼板三角感應加熱的電磁熱耦合模型，該數值模型為進一步應用固有應變法預測鋼板變形提供了條件。

1.1 實驗布置

在大連理工大學造船工藝實驗室進行加熱實驗，輥彎板的曲率半徑為2 000 mm，鋼板尺寸及加熱的工藝參數見表1，實驗方案布置見圖2，距離加熱線中間偏右側20 mm處的P點為溫度測量點，通過測量加熱線兩側11對測量點的距離變化得到加熱前后的橫向收縮量。

表1 感應加熱的工藝參數

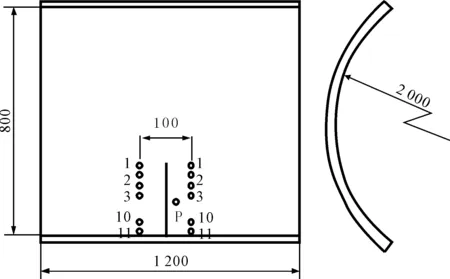
圖2 實驗布置和測量方案

三角感應加熱路徑見圖3，即先線狀加熱而后折線加熱，從而實現三角加熱的效果。直線部分210 mm，速度v1為8 mm/s，折線加熱區域的長度90 mm，速度v2為9 mm/s。加熱過程中的局部現場見圖4，加熱結束后的鋼板表面見圖5，在靠近板邊處的加熱線區域大致呈三角形狀。

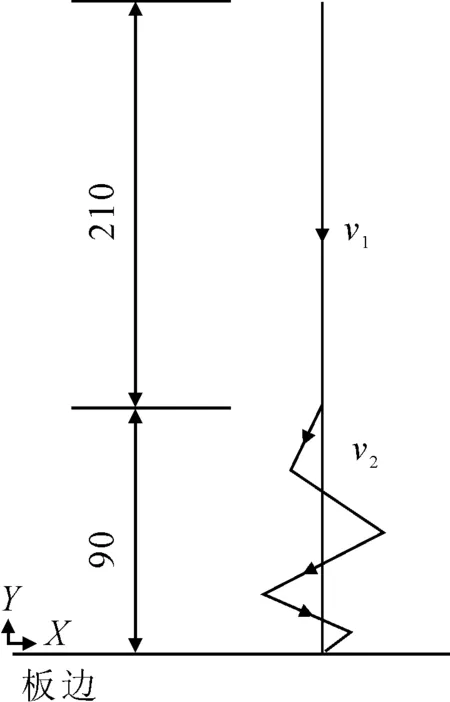
圖3 三角感應加熱路徑示意

圖4 三角感應加熱圖

圖5 三角感應加熱后鋼板表面

1.2 數值模擬

利用文獻[3-4]的輥彎板移動式感應加熱電磁-熱耦合有限元模型對加熱過程進行模擬。輥彎板的移動式感應加熱示意見圖6，移除空氣包后的橫截面模型見圖7。

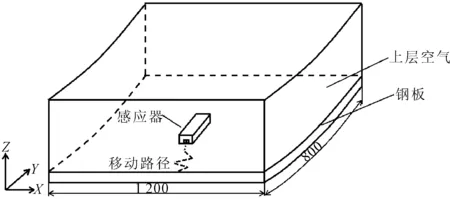
圖6 輥彎板的擺動感應加熱示意

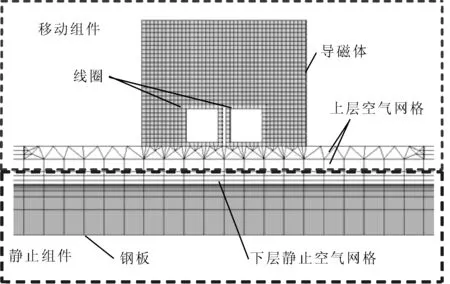
圖7 鋼板-感應器-空氣局部網格

整個加熱系統分為兩部分：①由感應器、遠場空氣包，以及上層運動空氣組成的移動組件；②由鋼板和下層靜空氣組成的靜止組件。該模型通過節點約束方程技術，實現了感應器、空氣間隙和鋼板之間相對移動的計算域求解過程，計算鋼板的溫度和變形，揭示鋼板和感應器之間的電磁耦合效應。

P點溫度實驗值和數值計算值的比較見圖8，橫向收縮的實驗值與數值計算結果的對比見圖9，兩者的平均相對誤差為15.3%。橫向收縮和溫度的變化情況都與實驗值一致，橫向收縮量的分布從板里到板邊呈逐漸增大的趨勢，表明所設計的三角感應加熱的路徑是合理的。

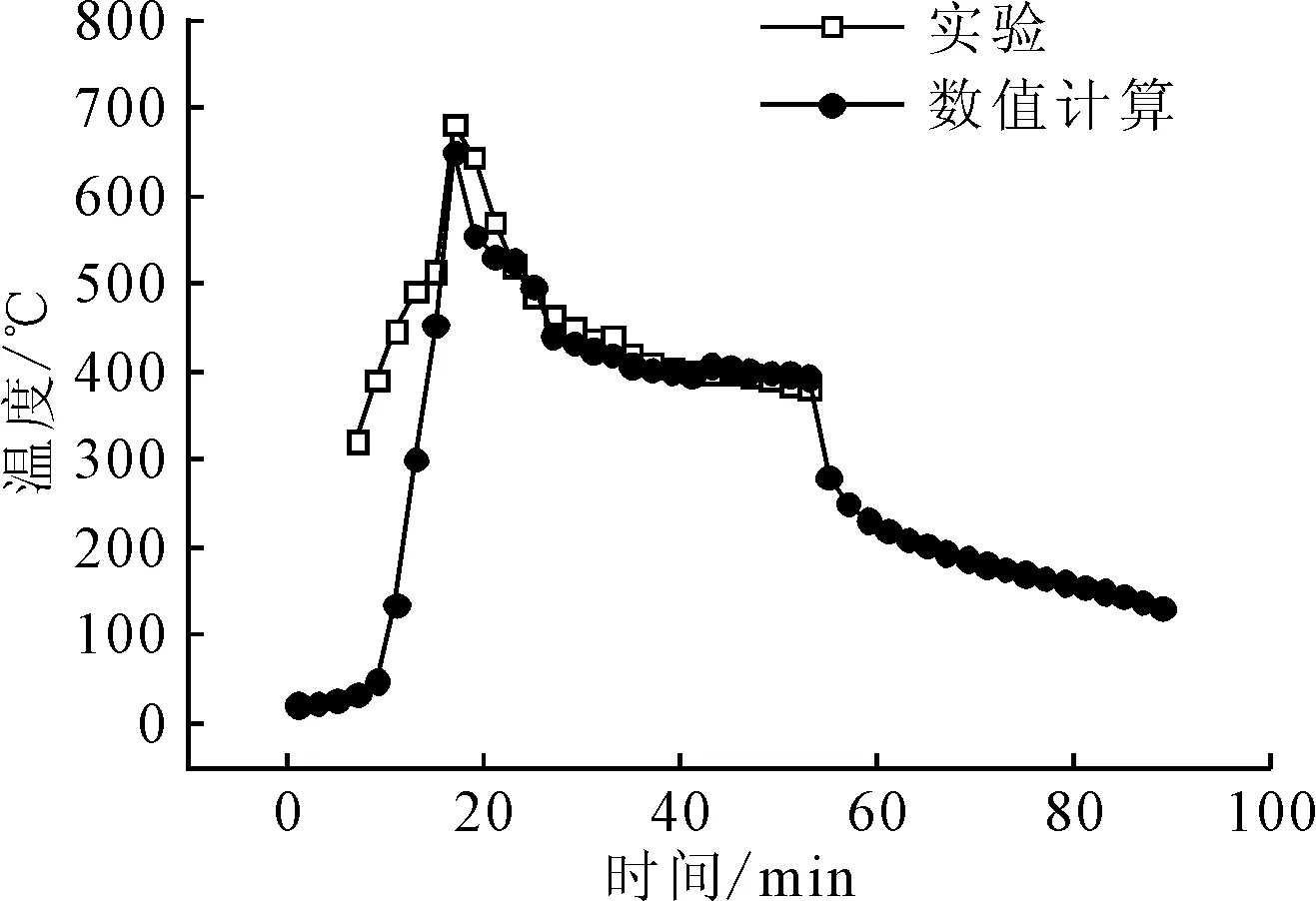
圖8 P點溫度的數值實驗對比

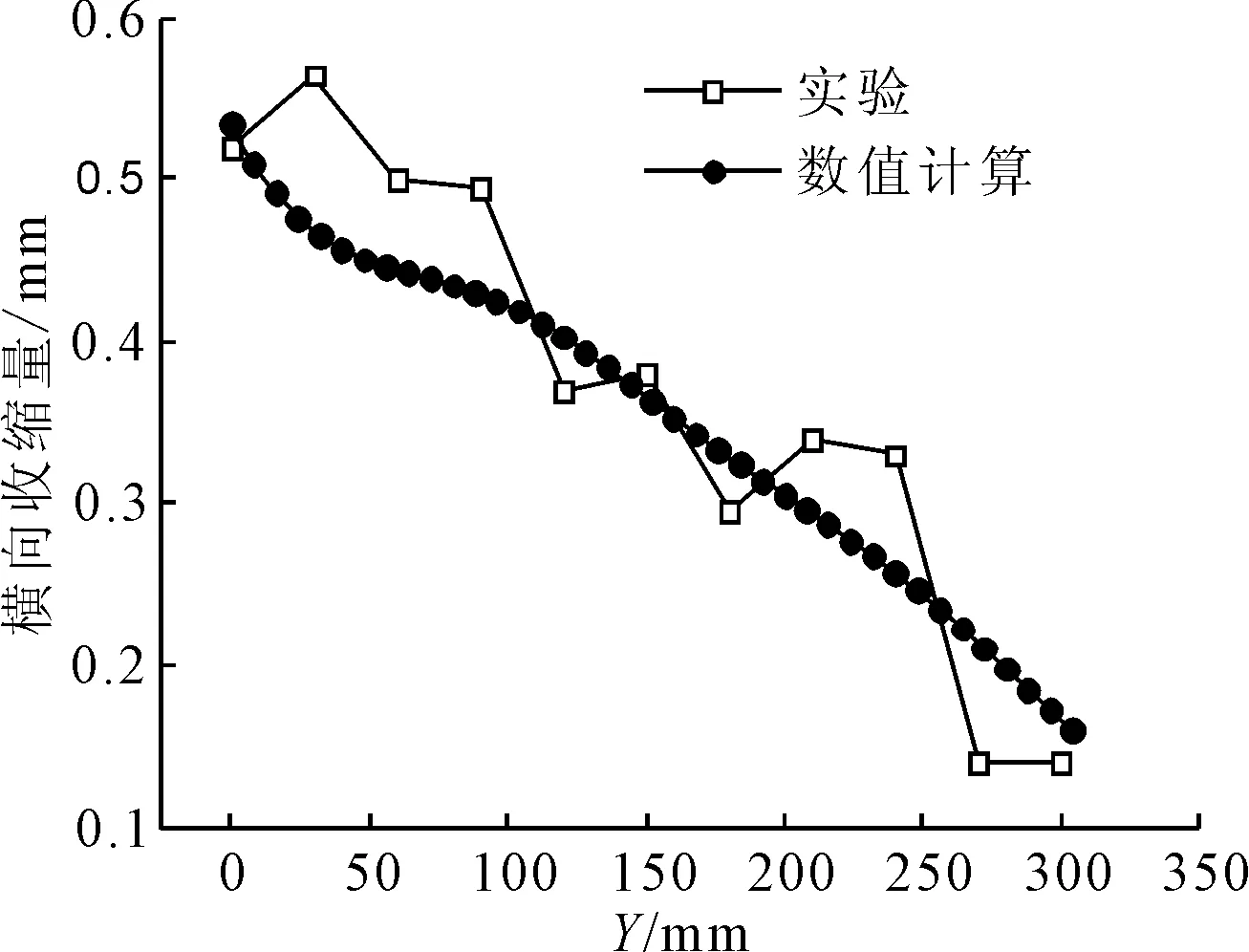
圖9 橫向收縮量比較

2 固有應變法應用

根據固有應變法，焊接過程中引起的無彈性的應變是固有應變ε*[5]，即

ε*=ε-εe

(1)

式中：ε為總應變量；εe為彈性應變。

固有應變是塑性應變εp、熱應變εt和相應變εθ三者之和，即

ε*=εp+εt+εθ

(2)

在實際加熱過程結束后，熱應變為零，如不考慮相變應變，固有應變就是塑性應變值。為了得到鋼板在加熱過程中的固有應變，將塑性應變在橫截面上積分得到固有應變之和，從而得到固有應變值[6]。

2.1 鋼板三角感應加熱固有應變的計算

對于輥彎板的三角感應加熱過程，對數值模擬得到的各個截面的塑性應變εp進行積分，得到橫向固有應變之和Wx和縱向固有應變之和Wy。

(3)

(4)

式中：εx為橫向固有應變；εy為縱向固有應變；A為固有應變區域沿垂直于加熱線方向的截面積。

對于殼單元或實體單元模型，在加載區域寬度為b，加載深度為h的情況下，定義加載區域的材料具有x、y方向的熱膨脹系數，熱膨脹系數值αx、αy分別為

(5)

(6)

在進行固有應變加載時使用溫度載荷法進行加載，在ANSYS軟件中設置材料的各向異性熱膨脹系數，然后施加單位溫度載荷，進行一次彈性計算獲得變形結果。溫度與應變的關系為

ε=α·Δt

(7)

式中:α為材料熱膨脹系數;Δt為單位溫度載荷，設置為1 ℃;ε為產生的熱應變數值。

沿著加熱線每隔15 mm選取一個截面，共20個截面，提取每個截面的節點塑性應變值，積分后得到橫向和縱向固有應變積分曲線見圖10。

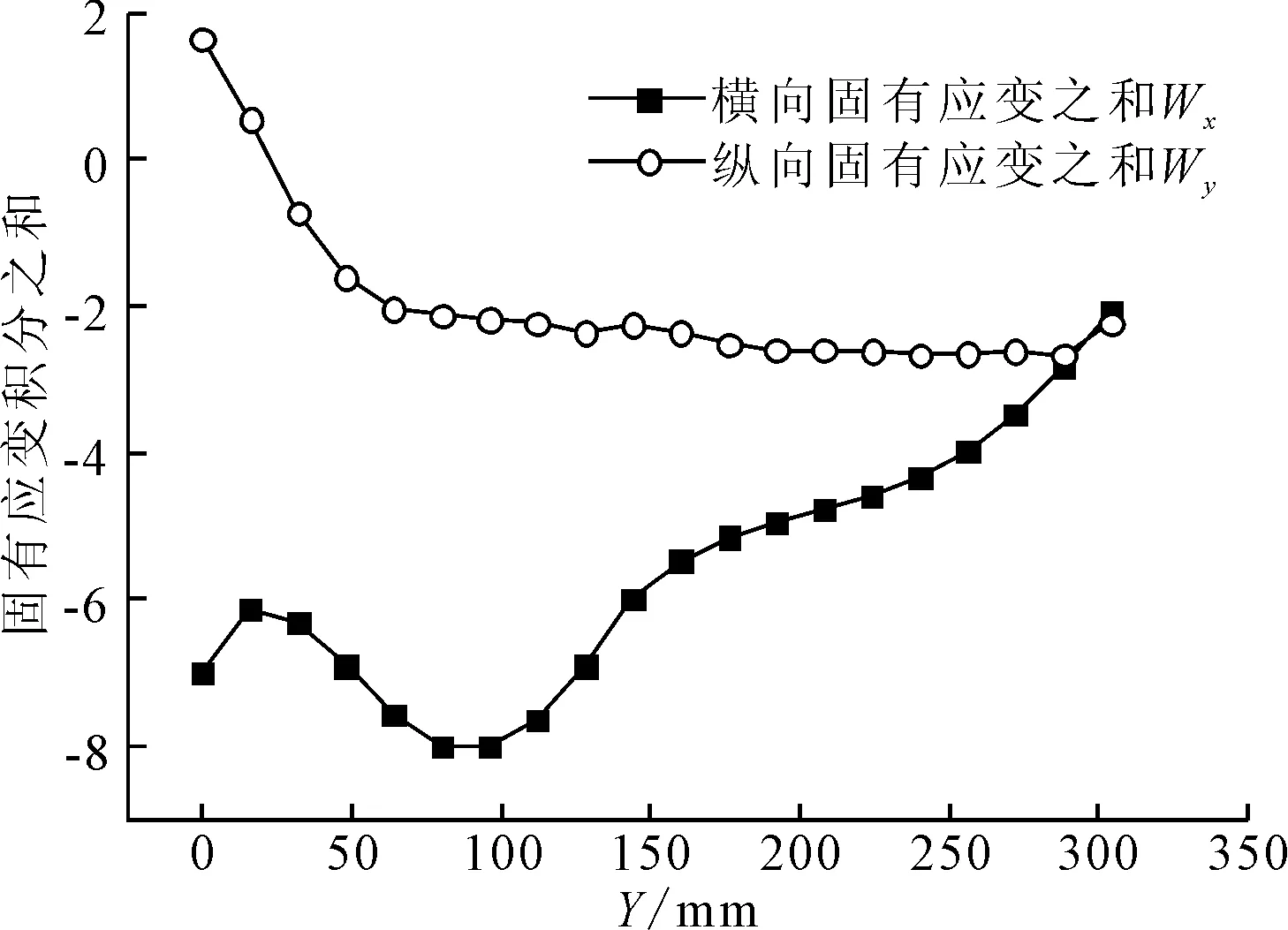
圖10 固有應變積分

可以看出橫向和縱向固有應變積分曲線沒有明顯的變化規律，因此加載固有應變時必須考慮其實際的分布規律。這一點不同于焊接產生的固有應變，因為焊縫長度足夠長，超過臨界焊接長度后固有應變有穩定值[7]，可以用平均固有應變來進行加載。

首先加熱線長度是有限的；另外，三角加熱的加熱路徑決定了鋼板加熱后產生非均勻的固有變形分布。鑒于此，在彈性有限元計算時須加載實際的固有應變分布，而不能采用平均固有應變。

2.2 固有應變的加載

各截面處的塑性應變云圖見圖11。在板邊Y=0 mm處，固有應變集中分布區域寬度最大109.0 mm，Y=300 mm處寬度為44.2 mm，寬度值從板里向板邊逐漸增大。

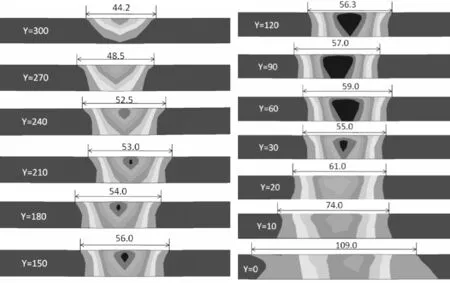
圖11 各截面橫向塑性應變云圖

鋼板彈性有限元分析模型見圖12。

圖12 鋼板整體網格圖

單元類型是SOLID 45單元。在加熱線附近的單元進行了網格細化，網格尺寸為1 mm，其他非加熱區域的網格為5 mm。在彈性有限元計算時采取圖13所示的加載方法，在每個加載段內分別加載不同的熱膨脹系數，經過多次計算，發現梯形加載和矩形加載的變形結果差別很小，而矩形加載卻更方便，這與文獻[8]結論一致。因此，將固有應變區寬度設置為50 mm。根據文獻[9]推導的考慮角變形的固有應變加載深度公式，此處加載深度為14 mm。

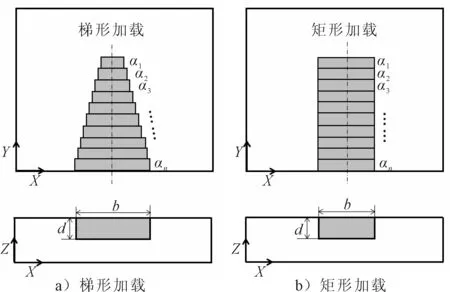
圖13 固有應變加載方法

圖14a)為橫向變形云圖，圖14b)為垂向變形云圖。彈性有限元計算的結果與熱彈塑性有限元模型的結果十分相近，計算時間約1 min，變形形狀也符合三角加熱的變形特點。

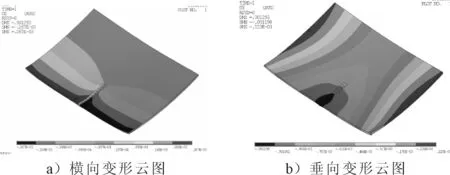
圖14 彈性有限元分析的位移云圖

橫向收縮量的對比見圖15，與實驗值相比較彈性有限元分析結果相對誤差為13.84%。加熱線中心線處的垂向位移對比見圖16，兩者的相對誤差為3.75%。面內變形和面外變形結果都符合工程要求，表明計算方法是可靠的。

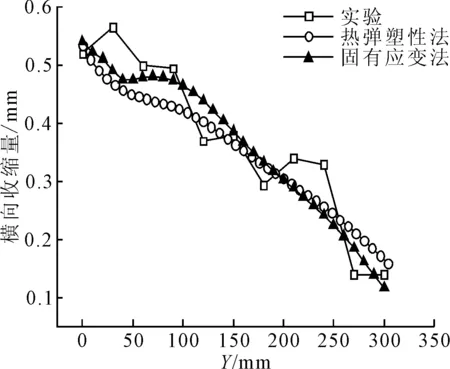
圖15 橫向收縮量比較

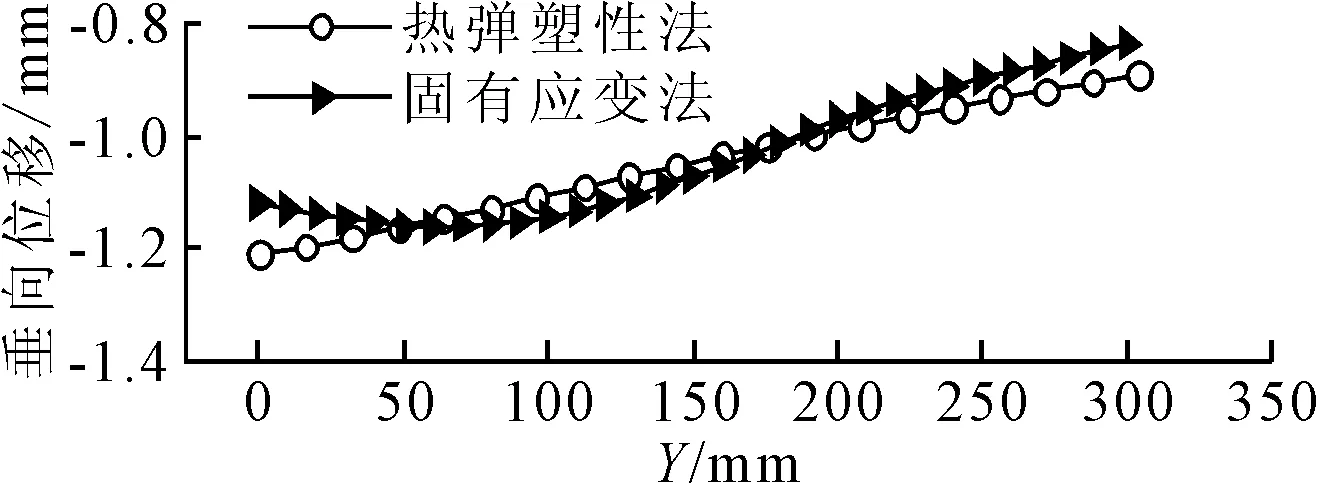
圖16 垂向位移比較

3 輥彎板三角感應加熱變形計算

帆形板成形時需要在鋼板上布置加熱線，基于固有應變法的彈性有限元分析方法計算鋼板的變形。因為鋼板表面有多條加熱線，在忽略加熱線彼此之間影響的前提下進行變形預測，實驗時設置加熱線間距為200 mm。

實驗用鋼板尺寸為1 200×800×20 mm，輥彎半徑2 000 mm，實驗方案見圖17。

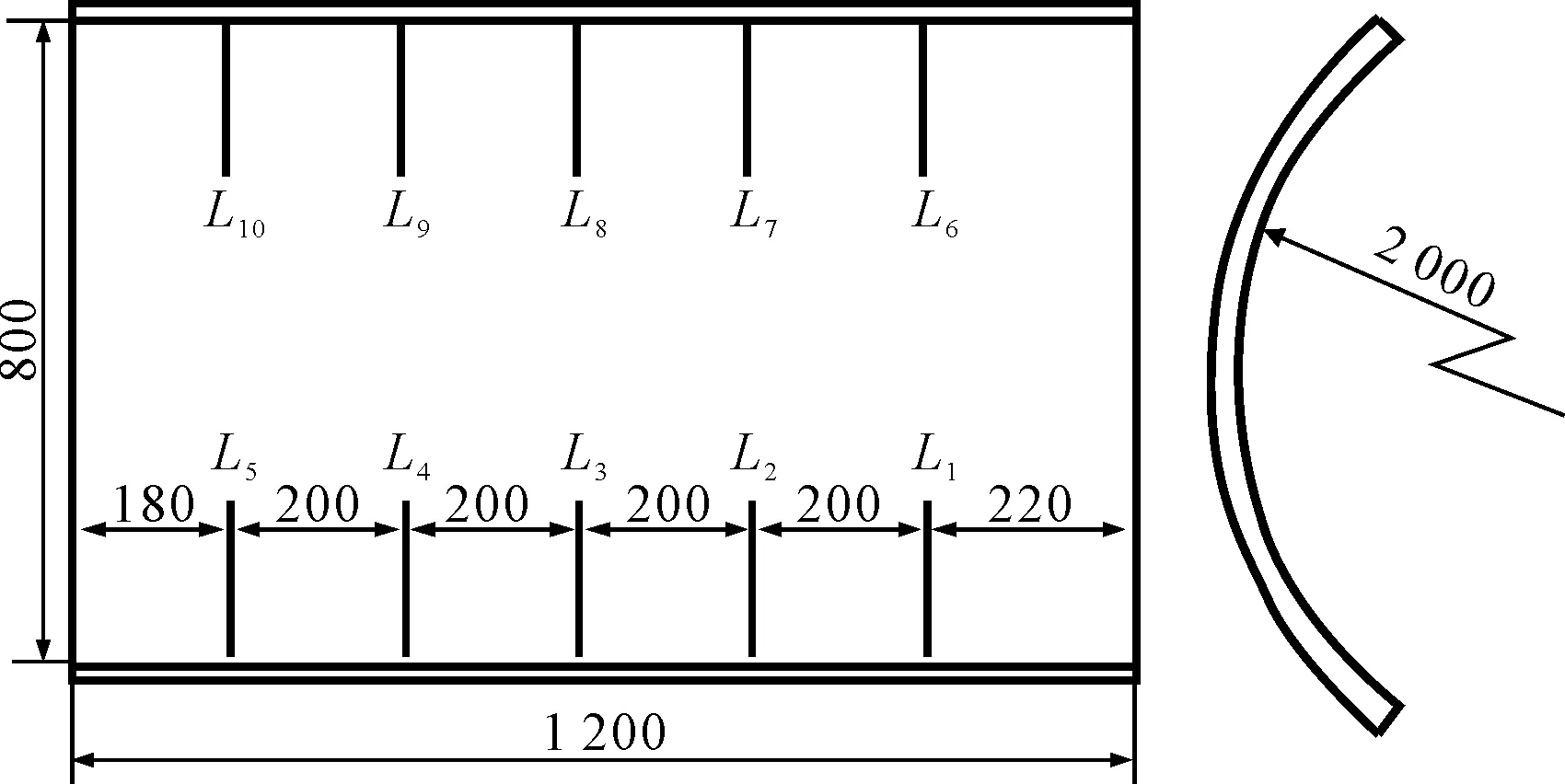
圖17 輥彎板三角感應實驗布置

采用靠近板邊處進行擺動加熱的三角加熱方式，共10條加熱線，加熱線的速度信息見表2，加熱線長度300 mm，空氣間隙9 mm，加熱功率50 kW。鋼板在全部加熱線完成之后的加熱效果見圖18。

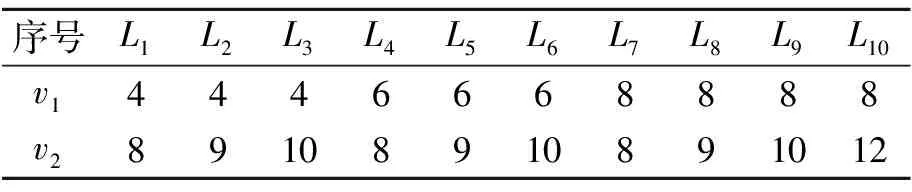
表2 加熱線速度信息 mm/s

圖18 加熱后的鋼板

輥彎板的彈性有限元模型見圖19，單元類型為SOLID45，均勻劃分鋼板網格，長度、寬度方向的網格尺寸均為10 mm，板厚方向的網格尺寸為0.5 mm。使用溫度載荷法進行固有應變的加載，在各個加熱線處的單元施加X、Y方向的熱膨脹系數，限制剛體位移約束四個頂點的X、Y、Z方向的自由度。

圖19 鋼板有限元模型

測量線示意圖見圖20。鋼板曲面的測量采用徠卡掌上全站儀S910進行測量，測量精度1.0 mm，測量現場見圖21，測量曲板坐標點數據后進行數據處理得到撓度值。鋼板的垂向位移云圖見圖22，鋼板中間區域的垂向位移較大。橫向變形云圖見圖23，收縮量在板邊處較大，鋼板整體呈現為帆形。

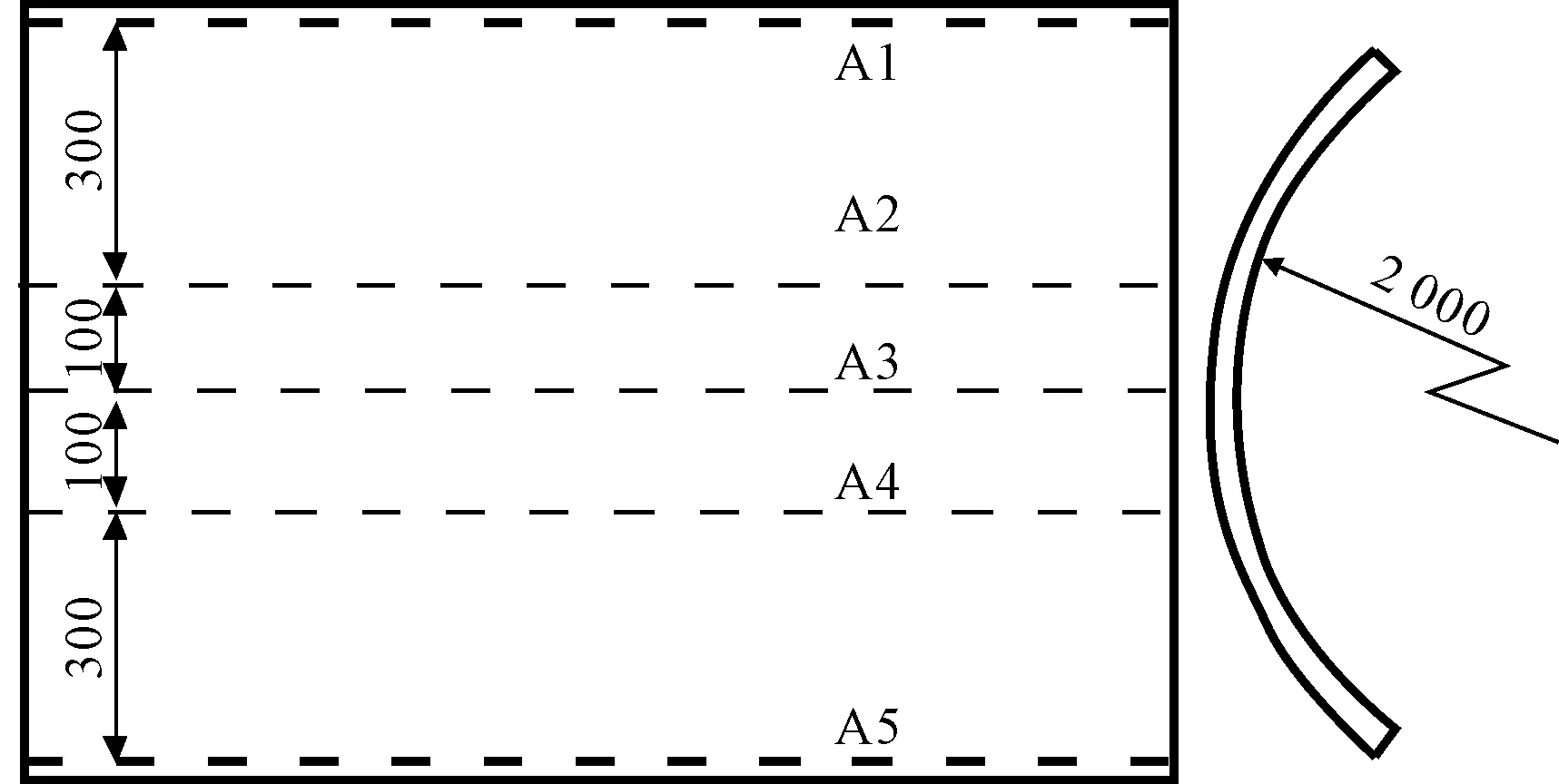
圖20 測量線布置示意

圖21 徠卡掌上全站儀S910測量鋼板曲面現場

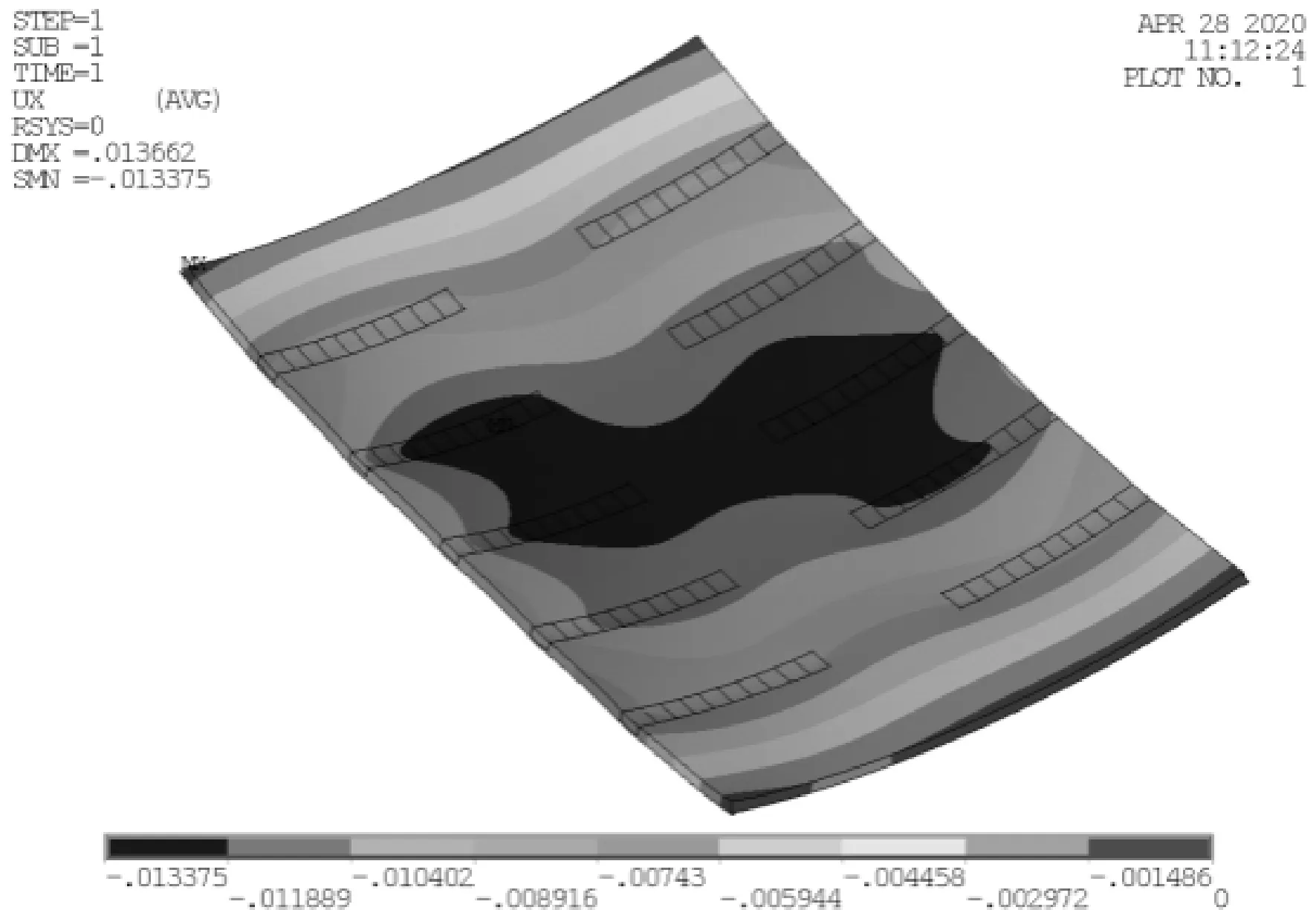
圖22 垂向變形云圖

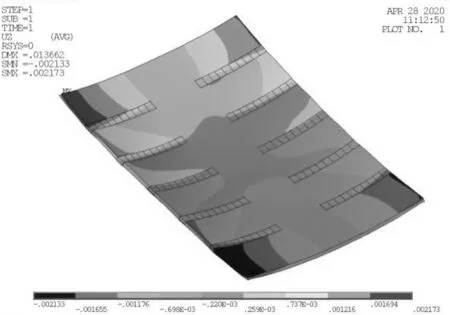
圖23 橫向變形云圖

各測量線的撓度測量值和計算值的對比見圖24，各計算值和實驗值一致。其中A1線與A5線位于縱向板邊位置，因為板邊處的固有應變值較大，計算出的垂向位移有波浪型的變化。A1～A5線的實驗值和計算值的平均相對誤差分別為：14.2%，10.7%，7.8%，13.4%，13.1%，誤差均在工程允許的范圍內。

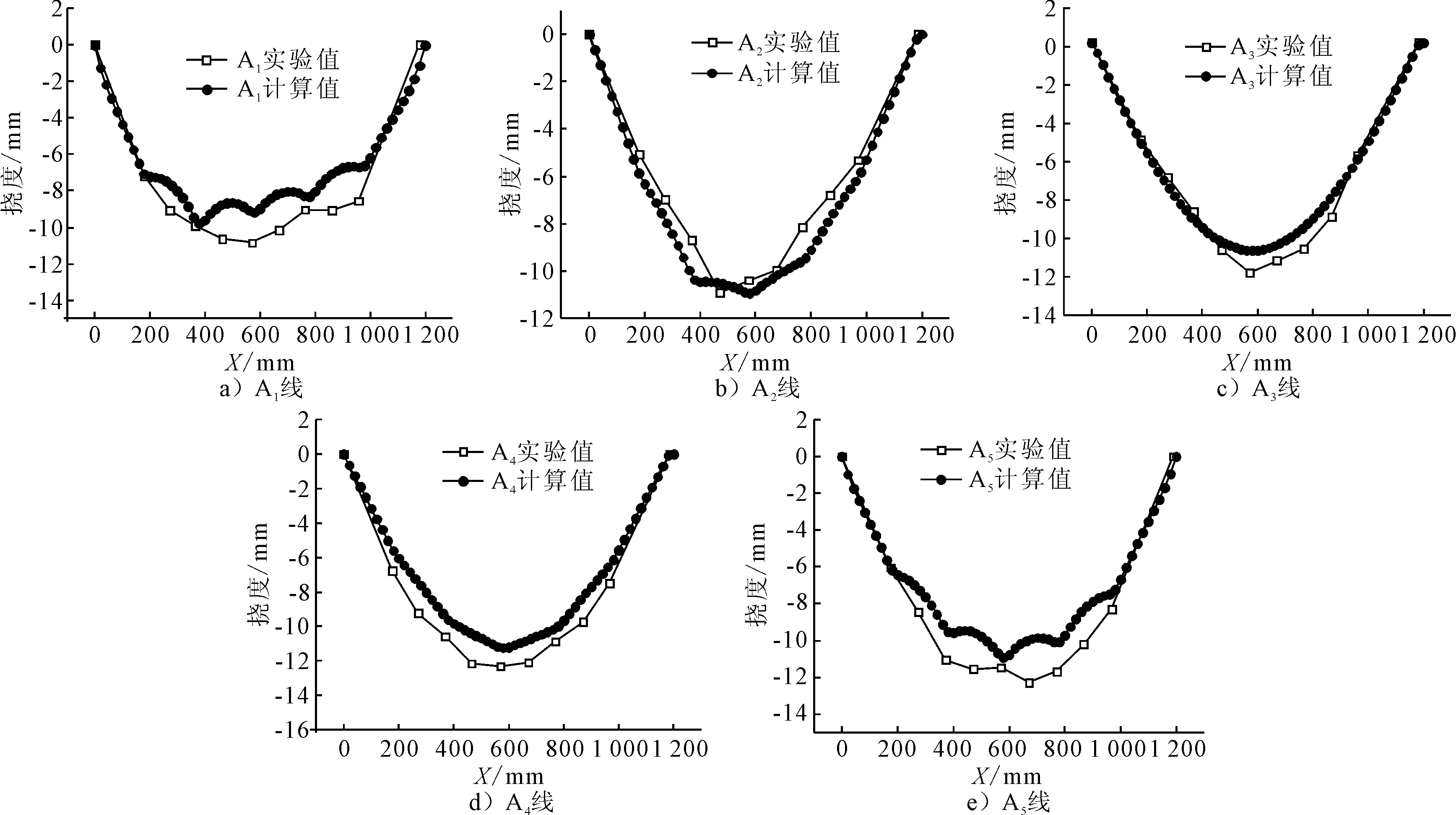
圖24 測量線的撓度值比較

對于多條加熱線的輥彎板變形計算，在忽略加熱線之間影響的前提下，基于固有應變法的彈性有限分析可以實現鋼板的整體變形計算，計算時間短，可以用于水火彎板工藝的整體變形預測。

4 結論

鋼板的三角感應加熱工藝產生復雜的固有應變分布規律，在進行固有應變的彈性有限元計算時在加載區域內需要加載實際的固有應變值，而不是平均固有應變。同時，進行輥彎板的多條加熱線的感應加熱實驗，使用建立的固有應變加載模型進行彈性有限元計算，計算的鋼板撓度值與實驗值相符，整體變形效果與實驗一致。