提升機盤式制動器碟簧剛度測量與預測研究

胡成名

中煤科工集團武漢設計研究院有限公司 湖北武漢 430064

施加于提升機制動盤上的正壓力是依靠碟形彈簧儲積的壓力能產生的。碟形彈簧在頻繁使用中，由于金屬的疲勞現象引起其剛度下降，若剛度急劇下降，則制動正壓力下降，制動過程越來越慢，進而導致制動失效；這將造成嚴重后果[1]。碟形彈簧的剛度是影響制動系統能否正常工作的重要因素，對其剛度的測量和預測研究有著重要的意義。

近年來，國內學者對碟簧的變形、疲勞壽命以及剛度都有不同的研究。張媛等人[2]利用 ANSYS 仿真軟件建立碟簧的有限元模型，進行疲勞分析，并預測其疲勞壽命。米月花等人[3]的研究表明，碟簧是物理非線性彈簧，載荷與變形呈非線性關系。王曉波等人[4]用LS-DYNA 有限元軟件對碟簧進行數值模擬，得到載荷和變形的關系曲線。上述研究大都基于軟件模擬，而沒有依據生產中的實測數據。筆者提出一種測量蝶簧剛度的方法，并依據實測數據對碟簧剛度進行有效預測。

1 碟簧剛度的測量方法

盤式制動器的力學模型[5]如圖 1 所示。

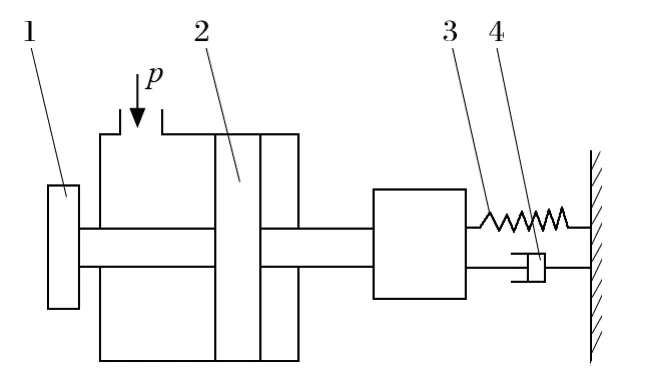
圖1 盤式制動器力學模型Fig.1 Mechanical model of disk brake

當液壓站油壓p(t) 為系統最高油壓時，制動器處于完全開閘狀態，盤式制動器的速度為 0，此時

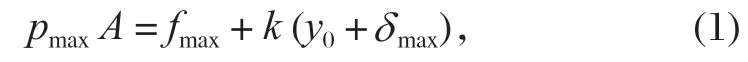
式中：pmax為液壓站最高油壓，MPa；A為液壓缸有效作用面積，mm2；fmax為液壓缸壁的摩擦阻力，N；k為碟簧的剛性系數，N/m；y0為碟簧的預壓縮量，mm；δmax為開閘時的閘瓦間隙，mm。

當制動器制動時，油壓p(t) 減小。盤式制動器運行δmax后，閘瓦剛剛貼上制動盤時，此時的油壓即為貼閘油壓pt，則有

貼閘后，油壓p(t) 繼續減小至系統殘壓pc時，制動力最大為Nmax，則有

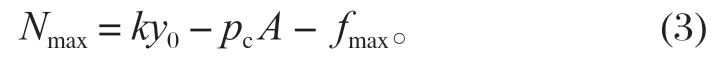
當制動器解除制動時，油壓p(t) 增大。當閘瓦剛剛離開制動盤時，碟簧的壓縮量為y0，此時的油壓即為開閘油壓pk，則有

聯立式 (1) 和式 (4) 可得

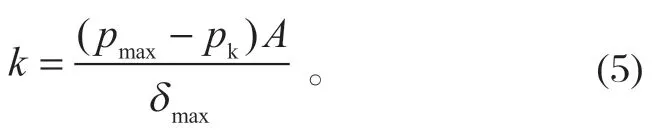
式(5) 表示了碟簧剛度的大小可以通過測得閘瓦的最大油壓pmax、開閘油壓pk和閘瓦間隙δmax來間接求得。

獲取開貼閘油壓的步驟如下：

(1) 將提升容器停在井筒中交鋒位置，然后鎖住滾筒；

(2) 在提升機閘瓦全制動狀態下，利用位移傳感器測出各閘的位移值，并在軟件中以一維數組存儲；

(3) 在閘瓦制動狀態下，緩慢扳動手柄，使油壓從殘壓緩慢上升到最大油壓，然后再使油壓從最大油壓緩慢下降，同時記錄各閘的位移變化和油壓變化，并與步驟 (2) 測出的各閘貼閘時的位移進行比較，求得開閘點和貼閘點的油壓。

圖2 所示為一次測量的數據曲線。

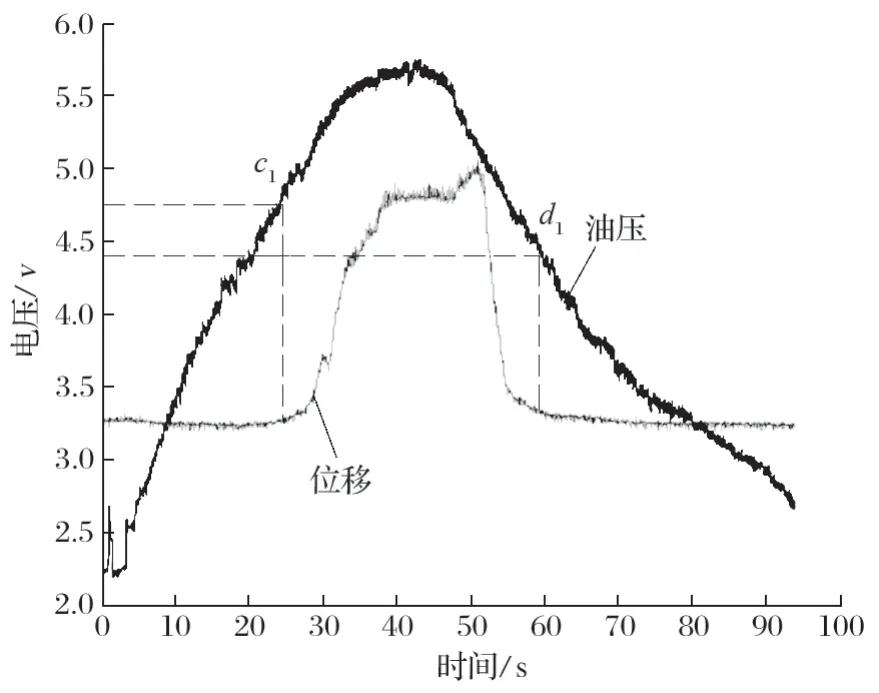
圖2 現場測試的位移與油壓曲線Fig.2 Variation curve of displacement and oil pressure in field test

由圖 2 可知：從殘壓上升到最大油壓用時 45 s，從最大油壓下降為殘壓用時 50 s，整個過程用時 95 s；該閘瓦的貼閘點和開閘點都比較明確，開閘點c1與貼閘點d1所對應的壓力傳感器的電壓輸出值分別為4.75 V 和 4.4 V。根據電壓與油壓的線性關系可知，兩點對應的油壓分別為 3.437 5 MPa 和 3 MPa。

利用閘瓦的最大油壓、開閘油壓和閘瓦間隙間接求得碟簧剛度的方法，對龍東煤礦副井某一碟簧剛度進行連續 6 個月測值，結果如表 1 所列。

表1 碟簧剛度Tab.1 Stiffness of disk spring ×105 N/m

間接法求得盤式制動器碟簧剛度，需要在停機狀態下進行，這影響了礦山企業的正常生產，由此可見，碟簧剛度預測的必要性。

2 GM(1,1) 建模方法

盤式制動器碟簧剛度的變化是一個緩慢的過程，也是一個非平穩的過程，難以用某一傳遞函數表示，可以認為其是一個灰色系統[6]。灰色系統過去和現在的信息綜合反映了諸多因素的綜合作用，包含著系統未來發展信息，可以用系統過去和現在的信息對未來進行預測；因此碟簧剛度未來隨時間的變化也可以用過去和現在的信息進行預測[7]。碟簧剛度是隨時間變化的序列值，筆者采用目前應用最為廣泛的數列預測模型 GM(1,1) 對碟簧剛度進行預測[8]。GM(1,1) 主要適用于等時間隔的離散數據的灰色建模，對于非等時間隔數據，可通過數學變換 (拉格朗日插值法、樣條插值法) 形成等間隔數據。其建模步驟如下。

2.1 累加生成碟簧剛度新數據列

設時間序列x(0)有n個觀察值，

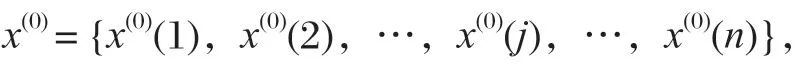
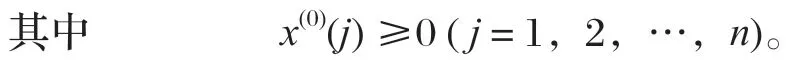
通常碟簧剛度的原始數據呈現離亂現象，灰色理論將無規律的原始數據累加生成，使其變為較有規律的生成序列。新序列用x(1)表示，

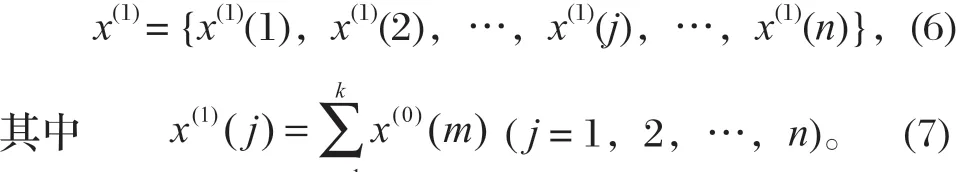
2.2 建立微分方程

建立白化形式的微分方程 GM(1,1)，

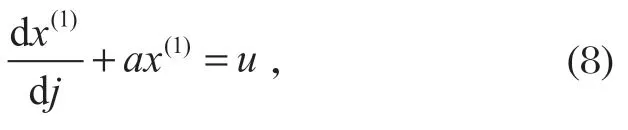
式中：a為發展灰數；u為內生控制灰數。

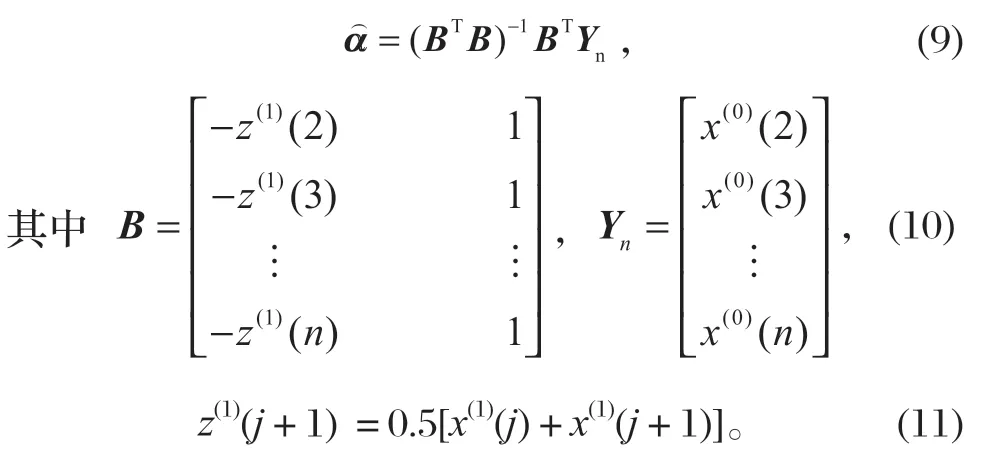
2.3 獲得預測模型

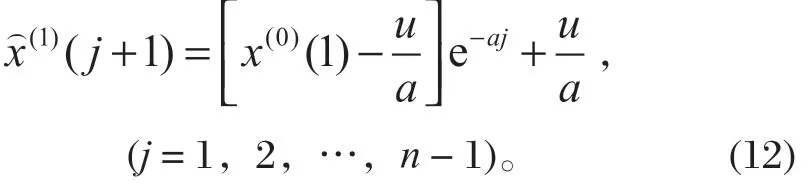
因灰色數列模型實際上是生成序列模型，對累加生成數據必須經過逆生成-累減還原后才能使用。進行累加生成的逆運算，還原預測數據列：

3 預測模型精度檢驗

在建立了碟簧剛度的預測模型后，需要對預測模型進行效果分析，檢驗和判斷預測模型的精度。

后驗差檢驗考慮了原始數據列的離散性，也考慮了擬合殘差離散性，同時小概率實踐考慮了擬合優度，因此筆者采用后驗差檢驗的方法對碟簧剛度的預測模型進行精度分析。

后驗差比值C與小誤差頻率P是后驗差檢驗的兩個重要指標，其中

式中：S2為殘差樣本的q(j) 的標準偏差；S1為實際數據樣本x(0)(j) 的標準偏差。

式中：x(mean) 為數據樣本x(0)(j) 的平均值。

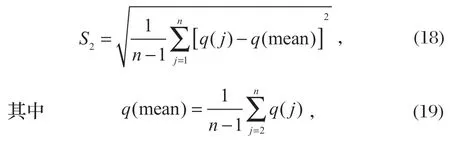
式中：q(mean) 為殘差樣本q(j) 的平均值。

小誤差頻率P的表達式為

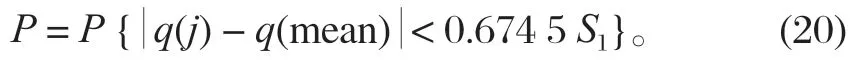
作為一個綜合指標，C越小越好，P越大越好。C小表明，盡管原始數據很離散，但模型所得計算值與實際值之差并不太離散[9]，一般要求C＜ 0.35。P大說明，殘差與殘差樣本平均值之差小于給定值 0.674 5S1的點較多，一般要求P＞ 0.95。按P和C的值綜合評判模型的精度，具體指標如表 2 所列。

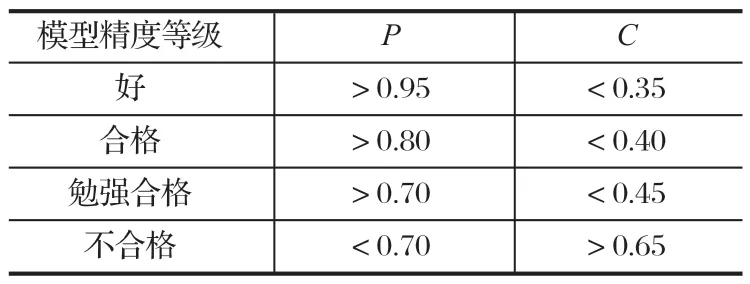
表2 模型精度等級指標Tab.2 Class indexes of model precision

4 碟簧剛度預測實例

采用 GM(1,1) 模型對龍東煤礦副井提升機制動系統碟簧剛度進行預測分析。

4.1 獲得預測模型

用x(0)表示碟簧剛度原始數據序列值，如表 1 所列。根據式 (7) 計算累加值，得到新序列x(1)，如表 3所列。

表3 數據列Tab.3 data sequence ×105 N/m

根據式 (11)，得到z(1)=(8.095，13.440，18.730，24.007 5，29.279)。

根據式 (10)，求得數據矩陣B、Yn：

將B和Yn代入式 (9)，得參數向量

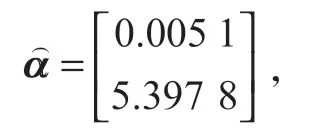
故a=0.005 1，u=5.397 8。

微分方程為

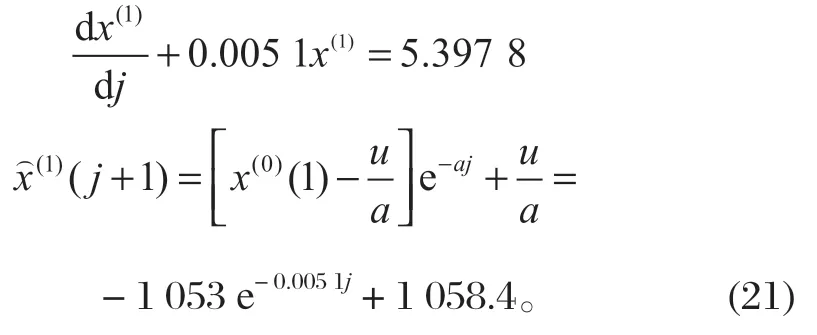
由式 (13) 求得^x(1)(j+1) 模型的計算值^x(1)與實際值x(1)，以檢驗模型精度，結果如表 4 所列。j=0，1，2，3，4，5。

表4 模型計算值和實際值的對比Tab.4 Comparison of predicted values of model and actual values

取^x(1)(0)=0，將^x(1)按式 (13) 作累減，檢驗模型還原值。還原后，模型還原值^x(0)與原始值x(0)的對比如表 5 所列。

表5 模型還原值與原始值的對比Tab.5 Comparison of reduced values of model and original values

故該碟簧剛度的預測模型為

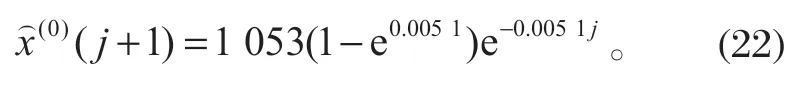
4.2 檢驗預測模型的精度

根據后驗差的檢驗標準，檢驗碟簧剛度的預測模型的精度。

已知碟簧剛度的原始數據序列x(0)(j)=(5.400，5.390，5.300，5.280，5.275，5.268)，根據式 (16)，計算碟簧剛度原始數據x(0)(j) 的標準差S1=0.060。

根據模型預測碟簧剛度后，實際值和預測值相減，所得的殘差序列q(j)=(0，0.033，0.029，0.022，0.000 3，-0.020)。根據式 (18)，計算殘差序列q(j)的標準差S2=0.020 6。C=S2/S1=0.343 ＜ 0.35。

殘差q(mean)=0.0211，|q(j) -q(mean)|=(0.021 1，0.011 9，0.007 9，0.000 9，0.020 8，0.018 9)，給定值為 0.674 5S1＝0.040 5，故P=1 ＞ 0.95。

由于C＝0.343 ＜ 0.35，P=1 ＞ 0.95，且相對殘差最大為 0.61%。根據表 2 可知，該碟簧剛度的預測模型預測精度較高。因此采用 GM(1,1) 模型對碟形彈簧進行剛度預測，預測效果較好。

5 結語

(1) 可以通過測得閘瓦的最大油壓、開閘油壓和閘瓦間隙，來求得盤式制動器蝶形彈簧的強度，并進行了有效測量。

(2) 選用灰色理論預測法對碟簧剛度預測進行建模，并以龍東礦副井碟形彈簧為例，采用 GM(1,1) 模型的建模方法，得到了該碟形彈簧剛度的預測模型，并通過后驗差檢驗的方法對預測模型精度進行了檢驗。檢驗結果表明，GM(1,1) 模型可靠，預測精度較高。

(3) 通過預測，可以對碟簧剛度的未來發展做出推測，判斷碟簧疲勞失效的時間，實現對碟簧剛度的提前預報和控制。