基于正弦函數處理新息的船舶模型參數辨識新算法
張顯庫,祝慧穎
大連海事大學 航海學院,遼寧 大連 116026
0 引 言
船舶的運動數學模型是船舶操縱性能預測、航海仿真和船舶運動控制器設計的基礎,具有10 個參數以上的Norrbin 或MMG 非線性數學模型的精度較高,但比較復雜;簡單的線性Nomoto 模型只有2 個參數,但精度稍低;具有4 個參數的非線性Nomoto 模型介于上述兩類模型之間,精度較高且不復雜,被船舶運動控制學者廣泛關注。非線性Nomoto 模型中的2 個非線性參數一般通過系統辨識獲得。新船在出廠后,通常只按國際標準要求做了滿舵回轉實驗和部分Z 形操縱實驗,如果采用此少量的船舶試驗數據進行系統辨識研究,給出船舶模型參數,其精度與用經驗公式估算的結果相近,不適用于模型精度要求較高的系統仿真或控制器設計。
目前,常用的系統辨識算法主要有最小二乘法、梯度辨識法、輔助模型辨識法等,這些算法都是利用典型的辨識數據進行系統的參數辨識。丁鋒[1]提出的系統辨識新論,將標量的誤差信息(也可稱為新息)變成了誤差信息向量,稱為多新息辨識算法,取得了較好的理論與應用成果;徐玲[2]利用動態窗數據將隨機梯度參數辨識方法中的標量新息擴展為新息向量,提出傳遞函數多新息隨機梯度參數估計方法,進一步提高了辨識精度;謝朔等[3]提出的一種改進的多新息擴展卡爾曼濾波參數辨識方法,通過引入遺忘因子以降低歷史干擾數據的累積影響,經此改進算法辨識的船舶響應模型參數更加精確;時振偉等[4]針對多元線性或非線性回歸系統,將耦合辨識思想與帶遺忘因子的有限數據窗辨識理論相結合,提出一種耦合帶遺忘因子有限數據窗遞推最小二乘辨識算法,該算法計算效率高,能夠快速跟蹤時變參數,獲得精確的參數估計;孫功武等[5]提出了一種基于模糊控制的動態遺忘因子遞推最小二乘算法,該算法中的遺忘因子能夠根據參數辨識誤差進行實時修正, 但僅對單輸入輸出系統模型參數進行了辨識研究;劉艷君等[6]針對含有未知時滯的多輸入輸出誤差系統,結合正交匹配追蹤算法和輔助模型思想對最小二乘迭代算法進行改進,提出了一種輔助模型正交匹配追蹤迭代算法,該算法對采樣數據的需求量不大,且在噪聲水平不高的情況下可以獲得精度較高的時滯估計與參數估計;焦慧方等[7]針對多變量耦合系統參數辨識,在傳統最小二乘法基礎上,提出了一種帶遺忘因子交替廣義最小二乘法,實現了無偏估計,并且簡化了計算;黃旭等[8]基于多新息辨識理論與隨機梯度辨識算法理論,結合變遺忘因子,提出了基于變遺忘因子多新息隨機梯度算法的雙饋電機參數辨識方法,相比最小二乘辨識方法減少了計算工作量,相對于隨機梯度辨識方法提高了辨識速度;鄭涵等[9]針對傳統擴展卡爾曼濾波方法的不足, 提出了一種新型的反饋粒子濾波算法,其收斂速度更快,穩定性更好,并應用到船舶運動數學模型的參數辨識中。以上文獻的研究重點集中在提高收斂速度、辨識效率和辨識精度方面,取得了一定的研究成果,但是在樣本數據較少的情況下,辨識效果并不理想。Zhang 等[10-11]提出了非線性反饋控制的思想,用非線性函數處理誤差并用于船舶運動控制,取得了良好的控制及節能效果。
本文將結合新息辨識算法[1]和非線性反饋控制[10-11]2 種創新思想,在最小二乘算法的基礎上,采用非線性正弦函數對新息進行處理后再進行參數辨識,通過仿真試驗驗證該算法在數據樣本少的情況下的計算速度及辨識精度,以期改善最小二乘辨識算法在數據樣本少時的辨識精度。
1 問題分析
圖1 給出了非線性新息辨識算法計算過程示意圖。其主要原理為對最小二乘等傳統辨識算法進行改進,將其誤差信息(新息)用正弦函數進行非線性處理,其他辨識過程保持不變,使用小樣本數據即可辨識出較為準確的結果。
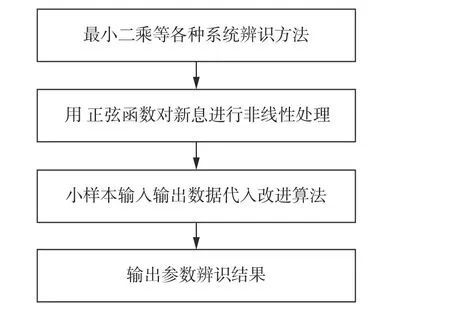
圖1 非線性新息辨識算法計算過程示意圖Fig. 1 Schematic diagram of calculation process of nonlinear innovation identification algorithm
2 船舶數學模型的建立

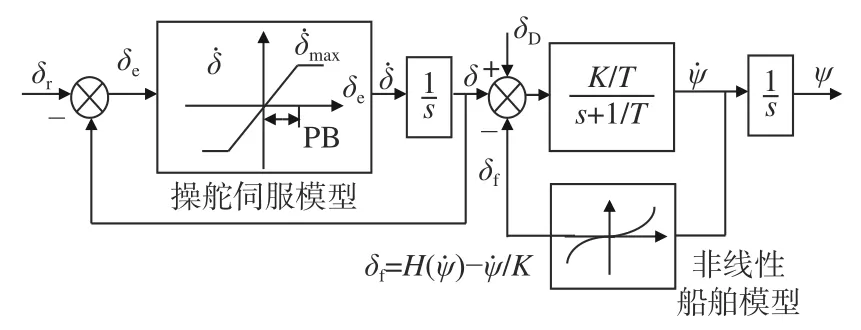
圖2 非線性的船舶運動數學模型Fig. 2 Nonlinear mathematical model of ship motion

3 非線性新息改進的最小二乘算法
常規的最小二乘法 (least square,LS) ,如式(3)所示:

多新息最小二乘法(muli-innovation least square,MILS)[1],將最小二乘遞推算法中每次遞推使用的單新息標量擴展為一定長度的多新息向量,從而在保證辨識精度的前提下提高參數在線辨識的收斂速度。本研究受其思想啟發將新息進行非線性處理。
式(5)中,Ud未經任何處理,直接參與系統辨識。受到非線性反饋方法的啟發,將新息經正弦函數的非線性處理后再參與模型參數辨識,非線性辨識參數的算法調整為式(6):

4 仿真驗證與結果分析
4.1 “育鯤”船
本文以大連海事大學教學實習船“育鯤”船為對象建立船舶數學模型,數學模型采用式(1)的非線性Nomoto 模型,船舶參數如表1 所示。
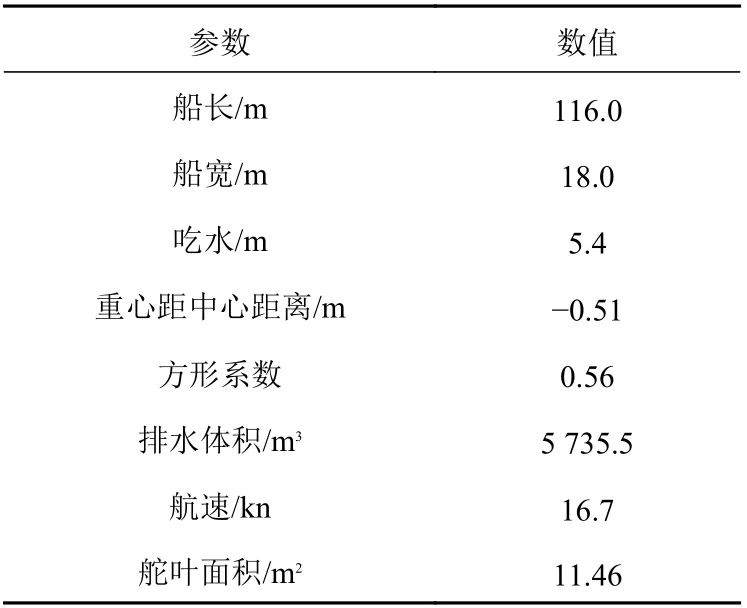
表1 “育鯤”船船舶參數Table 1 Yukun ship particulars
“育鯤”船的非線性Nomoto 模型參數(K,T,α, β)的真值可根據表1 給出的船舶參數通過理論計算得出[13-14],結果如表2 所示。

表2 “育鯤”船模型參數真值Table 2 True value of Yukun ship model parameters


利用獲得的26 組仿真數據進行 α,β的非線性參數辨識,用于驗證辨識算法精度是否滿足要求。對于α 的辨識A=1,ω=0.87;對于β的辨識A=1.45,ω=1.14。比較最小二乘法和非線性新息改進的最小二乘法對非線性參數 α、β 的辨識效果,結果如圖3 所示。由圖3 可見,最小二乘法的辨識結果中α=15.94,β=17 220.81,α 和β 的誤差分別為12.1% 和23.3%,平均誤差17.7%;非線性函數改進的最小二乘法的辨識結果中α=14.11,β=21 729.58,α 和β 的誤差分別為0.8% 和3.2%,平均誤差只有2.0%,模型辨識精度可達98.0%。
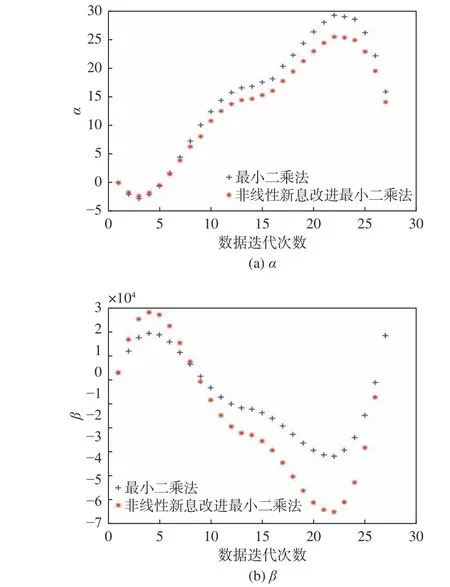
圖3 最小二乘法和非線性新息改進最小二乘法對“育鯤”船的辨識效果Fig. 3 Identification effect of LS method and nonlinear innovation improved LS method on Yukun ship
由此可見,在只有26 組仿真數據的前提下,非線性新息改進的最小二乘法具有較高的辨識精度,相對于最小二乘法的辨識精度提高了15.7%。
4.2 “育鵬”船
為了進一步檢驗非線性新息改進最小二乘法的辨識效果,采用大連海事大學另一艘教學實習船“育鵬”船進行驗證,A,ω 保持不變。“育鵬”船的船舶參數和模型參數真值如表3 和表4 所示。
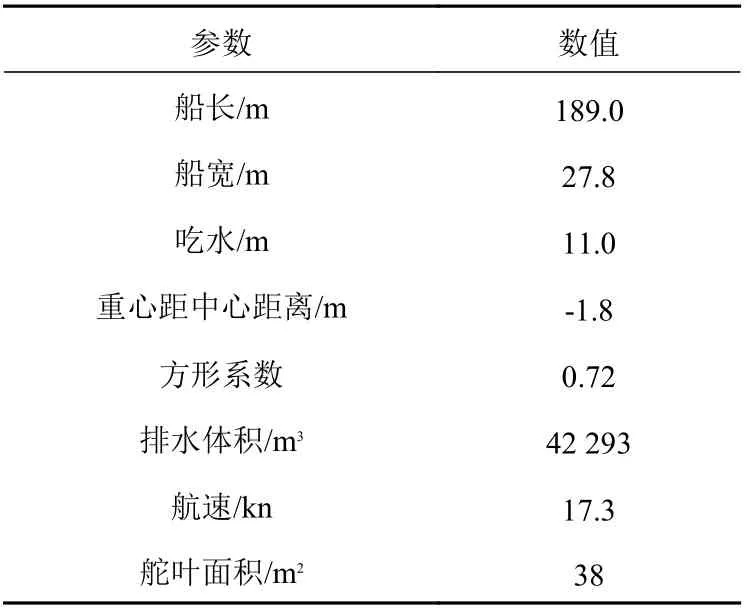
表3 “育鵬”船船舶參數Table 3 Yupeng ship particulars
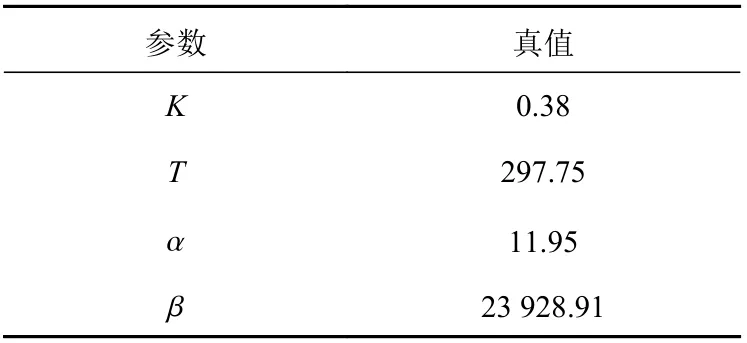
表4 “育鵬”船模型參數真值Table 4 True value of Yupeng ship model parameters
同理,用最小二乘法和非線性新息改進最小二乘算法對“育鵬”船的非線性參數 α,β進行辨識,結果如圖4 所示。
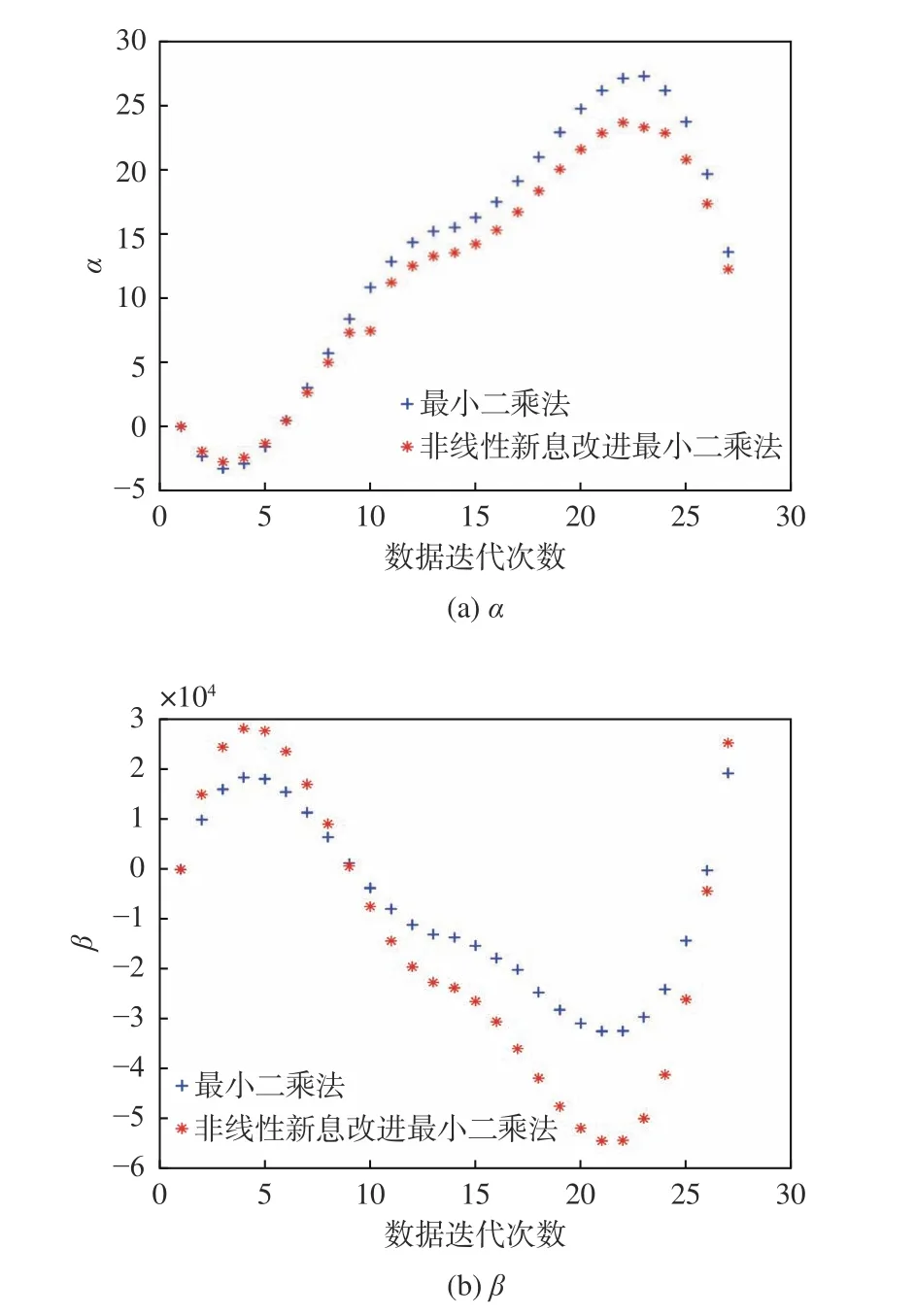
圖4 最小二乘法和非線性新息改進最小二乘法對“育鵬”船的辨識效果Fig. 4 Identification effect of LS method and nonlinear innovation improved LS method on Yupeng ship
由圖4 可見,最小二乘法的辨識結果中α=13.59,β=19 270.41,α 的誤差為13.7%,β 的誤差為19.5%,平均誤差16.6%;非線性新息改進最小二乘法辨識結果中α=12.12,β=25 342.29,α 的誤差為1.4%,β 的誤差為5.9%,平均誤差3.7%,即模型辨識精度可達96.3%。
因此,在樣本數據較少的情況下,以“育鵬”船為對象進行仿真驗證,非線性新息改進最小二乘算法的辨識精度仍然比最小二乘法的提高了12.9%,進一步證明了該算法的有效性和普適性。此外,本算法因只需要少量的數據樣本,計算量減少,故客觀上提升了辨識速度。
5 結 論
本文將多新息系統辨識和非線性反饋控制思想相結合,提出了一種基于非線性新息的船舶模型參數辨識算法。通過對比和辨識仿真驗證,得出了以下結論:
1) 該算法辨識所需樣本數據較少。在仿真驗證過程中只采用了26 組仿真數據,辨識準確度可達到96%以上,為小樣本數據情況下的參數辨識提供了參考。
2) 通過2 艘船的辨識驗證,該算法比最小二乘法的辨識精度提高了12% 以上,拓展了最小二乘法的應用范圍。
3) 該算法的辨識速度較快。
本研究給定模型參數,是為了驗證辨識算法的有效性和準確性,下一步可實際采集少量實船試驗數據樣本,用本研究結果直接辨識船舶模型,以克服理論計算模型計算復雜且精度不高的缺點。此外,還可將多新息和非線性新息相結合,進行多模型、多參數的船舶模型辨識研究。

