基于漸進(jìn)結(jié)構(gòu)優(yōu)化算法的橋梁找型工作研究
王 軍,王 萍,馮昭亮
(1.西安市政設(shè)計(jì)研究院有限公司,陜西 西安 710068;2.內(nèi)蒙古阿拉善盟公路運(yùn)輸維護(hù)中心,內(nèi)蒙古 阿拉善盟750306;3.西安航天城市政公用發(fā)展有限公司,陜西 西安 710005)
0 引言
結(jié)構(gòu)優(yōu)化設(shè)計(jì),通俗點(diǎn)說(shuō),就是選擇較好的設(shè)計(jì)方案并進(jìn)行設(shè)計(jì)。從廣義上說(shuō),應(yīng)當(dāng)是用系統(tǒng)的、目的定向和良好標(biāo)準(zhǔn)的設(shè)計(jì)過(guò)程來(lái)實(shí)現(xiàn)對(duì)所選結(jié)構(gòu)形式、外形尺寸、采用材料等的設(shè)計(jì)[1-2]。拓?fù)鋬?yōu)化時(shí),在限定條件較少,如尚不明確構(gòu)件尺寸、構(gòu)件之間的連接方式時(shí),可以利用拓?fù)鋬?yōu)化工具進(jìn)行橋梁結(jié)構(gòu)的找型工作,得到橋梁結(jié)構(gòu)材料最優(yōu)分布的橋型方案。
1 拓?fù)鋬?yōu)化及其基本原理
優(yōu)化設(shè)計(jì)按所選設(shè)計(jì)變量類型的不同可分為截面(尺寸)優(yōu)化、形狀優(yōu)化和拓?fù)鋬?yōu)化。其中,拓?fù)鋬?yōu)化屬優(yōu)化設(shè)計(jì)的概念設(shè)計(jì)階段。其目的主要體現(xiàn)在結(jié)構(gòu)選型和結(jié)構(gòu)布置上,即在滿足各種約束條件下,去除不必要的構(gòu)件和材料使結(jié)構(gòu)在規(guī)定意義上達(dá)到最優(yōu),屬于優(yōu)化設(shè)計(jì)的最高階段,難度也最大。因此,拓?fù)鋬?yōu)化才是真正意義上的創(chuàng)造結(jié)構(gòu)[3]。
對(duì)于設(shè)計(jì)人員,只要將有限元分析軟件與優(yōu)化設(shè)計(jì)方法結(jié)合起來(lái),并把工程實(shí)際問(wèn)題合理地轉(zhuǎn)化為優(yōu)化模型,就可以利用相關(guān)計(jì)算方法很好地完成優(yōu)化設(shè)計(jì)。借助ANSYS 軟件強(qiáng)大的優(yōu)化分析功能,能夠很好地完成既定的優(yōu)化目標(biāo)。ANSYS 的優(yōu)化模塊中三大優(yōu)化變量為設(shè)計(jì)變量、狀態(tài)變量、目標(biāo)函數(shù)[4]。
1.1 設(shè)計(jì)變量
在結(jié)構(gòu)優(yōu)化設(shè)計(jì)方案諸多變量中,可以變化的量為設(shè)計(jì)變量。通過(guò)不斷改變其值而逐漸得到最終的優(yōu)化結(jié)果。ANSYS 分析軟件最多可以定義60 個(gè)設(shè)計(jì)變量。
1.2 狀態(tài)變量
狀態(tài)變量為設(shè)計(jì)變量的函數(shù),也可以獨(dú)立于設(shè)計(jì)變量。狀態(tài)變量必須滿足一定的約束條件。約束條件可以是等式或不等式。避免狀態(tài)變量的上限和下限取值過(guò)于接近,造成無(wú)解現(xiàn)象。ANSYS 分析軟件中最多可以定義100 個(gè)狀態(tài)變量[5]。
1.3 目標(biāo)函數(shù)
目標(biāo)函數(shù)是要盡量減小的函數(shù)。它必須是設(shè)計(jì)變量的函數(shù)。在ANSYS 優(yōu)化程序中,它總是以最小化為目標(biāo)函數(shù)。如果實(shí)際工程問(wèn)題中所求目標(biāo)函數(shù)為極大值,可以通過(guò)取倒數(shù)來(lái)實(shí)現(xiàn)。ANSYS 程序要求優(yōu)化過(guò)程中只能有一個(gè)目標(biāo)函數(shù)。
2 漸進(jìn)結(jié)構(gòu)拓?fù)鋬?yōu)化方法
2.1 拓?fù)鋬?yōu)化方法
結(jié)構(gòu)拓?fù)鋬?yōu)化可分為離散型和連續(xù)型。目前,連續(xù)體結(jié)構(gòu)為拓?fù)鋬?yōu)化主要的研究對(duì)象[6-7]。連續(xù)結(jié)構(gòu)拓?fù)鋬?yōu)化常用的研究方法有均勻化法、變密度法和漸進(jìn)結(jié)構(gòu)優(yōu)化方法(Evolutionary Structural Optimization,簡(jiǎn)稱ESO)等。
ESO 是近年來(lái)興起的一種解決各類結(jié)構(gòu)優(yōu)化問(wèn)題的數(shù)值方法。ESO 技術(shù)自1992 年提出以來(lái),在國(guó)際上反響很大[5]。該方法由于能夠很好地與有限元程序進(jìn)行對(duì)接,能夠獲得較可信的優(yōu)化結(jié)果。該算法基本原理為:通過(guò)構(gòu)建一定的準(zhǔn)則(應(yīng)力、位移/ 剛度、頻率),將結(jié)構(gòu)中那些低效的單元慢慢刪除,通過(guò)不斷地重復(fù)迭代計(jì)算,獲得一個(gè)最佳的結(jié)構(gòu)形式[8]。由于該方法所依據(jù)準(zhǔn)則簡(jiǎn)單、物理概念明確,因此很快擴(kuò)展到多工況、非線性、動(dòng)力等復(fù)雜問(wèn)題。
2.2 基于應(yīng)力和剛度共同約束的ES O
絕大多數(shù)的工程結(jié)構(gòu)在運(yùn)行狀態(tài)下都同時(shí)受到應(yīng)力和位移兩方面的約束控制。橋梁結(jié)構(gòu)在正常使用狀態(tài)下不僅要滿足應(yīng)力約束條件,還要滿足撓度約束條件。所以,研究這類問(wèn)題更有工程應(yīng)用價(jià)值。
對(duì)優(yōu)化結(jié)構(gòu)進(jìn)行有限元分析后,如果所求的單元位移靈敏度數(shù)較低,則表明需要?jiǎng)h除較多的單元,單元的刪除率也相應(yīng)較高。如果所求單元的應(yīng)力較低,則表明結(jié)構(gòu)中有較多單元處于低應(yīng)力狀態(tài),相應(yīng)的單元?jiǎng)h除率也會(huì)較高。

基于以上分析,在位移和應(yīng)力兩方面控制下的單元綜合靈敏度公式可表示為[8]:式中:αi,z為單元綜合靈敏度;為每個(gè)單元Von Mises 應(yīng)力;為單元最大Von Mises 應(yīng)力;αi為每個(gè)單元位移靈敏度數(shù);αmax為單元最大位移靈敏度數(shù)。
由于αi,z的取值范圍為0<αi,z<1,所以單元應(yīng)力值和位移靈敏度數(shù)有相同的數(shù)量級(jí),不會(huì)產(chǎn)生較大的計(jì)算誤差。
以上所分析的都是結(jié)構(gòu)在單工況下的優(yōu)化問(wèn)題。而橋梁結(jié)構(gòu)通常會(huì)同時(shí)受到汽車荷載、人群荷載、溫度荷載等作用。對(duì)于多荷載工況,單元的刪除準(zhǔn)則為:每一個(gè)工況都滿足刪除準(zhǔn)則的單元才能被刪除。通過(guò)式(1)可以很容易計(jì)算出在不同荷載工況下,每個(gè)單元的綜合靈敏度數(shù),…,將其中最大值定義為這個(gè)單元的綜合靈敏度數(shù),即:式中,k 為總工況數(shù)。

3 截面拓?fù)鋬?yōu)化
3.1 單元模型的選取
對(duì)截面采用漸進(jìn)優(yōu)化算法時(shí),首先是將其離散成數(shù)量可觀的單元,使單元網(wǎng)格盡可能小,這樣得到的優(yōu)化結(jié)果越精確。單元網(wǎng)格的劃分要在建模階段完成。在優(yōu)化階段,總是對(duì)同一模型進(jìn)行反復(fù)迭代計(jì)算。研究發(fā)現(xiàn),最初選取的模型形狀能否代表所要進(jìn)行優(yōu)化的截面尤為重要,它直接影響到優(yōu)化的合理性和正確性。
截面的拓?fù)鋬?yōu)化可以分為平面應(yīng)力單元優(yōu)化和三維實(shí)體單元優(yōu)化。平面應(yīng)力單元優(yōu)化采用四節(jié)點(diǎn)矩形平面應(yīng)力單元計(jì)算,相對(duì)比較簡(jiǎn)單。有時(shí)候可將一些復(fù)雜的三維實(shí)體單元優(yōu)化問(wèn)題簡(jiǎn)化為平面應(yīng)變和平面應(yīng)力問(wèn)題,能獲得較好的優(yōu)化效果。
3.2 控制截面的選取
當(dāng)構(gòu)件受力并不復(fù)雜時(shí),采用結(jié)構(gòu)中具有代表性的截面,如受力最不利截面,對(duì)其進(jìn)行優(yōu)化,就能客觀地反映結(jié)構(gòu)真實(shí)的優(yōu)化后形狀。當(dāng)結(jié)構(gòu)受到復(fù)雜荷載作用時(shí),可以選擇多個(gè)控制截面進(jìn)行優(yōu)化,對(duì)不同控制截面的優(yōu)化結(jié)果進(jìn)行比較,從而得出最優(yōu)設(shè)計(jì)。根據(jù)已有的設(shè)計(jì)經(jīng)驗(yàn),首先考慮矩形截面為其初始設(shè)計(jì)截面。可以采取由結(jié)構(gòu)整體→局部截面→優(yōu)化后結(jié)構(gòu)整體這樣一個(gè)循環(huán)迭代過(guò)程。
3.3 設(shè)計(jì)區(qū)域的選取
設(shè)計(jì)區(qū)域的幾何布局是未知的,要通過(guò)拓?fù)鋬?yōu)化來(lái)確定其具體的位置形狀,所以該區(qū)域是可以刪除的區(qū)域。在優(yōu)化模型的建立時(shí),對(duì)于設(shè)計(jì)區(qū)域的幾何體,在劃分單元時(shí)盡量選用較為簡(jiǎn)單的單元形狀,以有利于減少迭代收斂的時(shí)間。
4 拓?fù)鋬?yōu)化實(shí)例
4.1 二維平面單元拓?fù)鋬?yōu)化典型算例
對(duì)于平面應(yīng)力單元的拓?fù)鋬?yōu)化,ANSYS 軟件分別提供了兩種拓?fù)鋬?yōu)化算法。第一種是以獲得結(jié)構(gòu)剛度最大為目標(biāo)的線性結(jié)構(gòu)靜力分析。第二種是以獲得結(jié)構(gòu)動(dòng)態(tài)剛度最大為目標(biāo)的模態(tài)分析。本算例為第一種形式。該算法的中心思想是結(jié)構(gòu)在靜力荷載作用下,在滿足體積縮減量約束條件的情況下,使得結(jié)構(gòu)剛度最大。該算法不考慮材料和結(jié)構(gòu)非線性,將結(jié)構(gòu)剛度最大定義為目標(biāo)函數(shù)。
拓?fù)鋬?yōu)化時(shí),尚不明確構(gòu)件尺寸、構(gòu)件之間的連接方式。在這種限定條件較少的情況下,可以利用拓?fù)鋬?yōu)化工具進(jìn)行橋梁結(jié)構(gòu)的找型工作。以下就是很好的典范。
4.2 模型的建立
在修建道路上需要建造一座鋼拱橋。該橋所在的空間形狀如圖1 所示。長(zhǎng)方形頂面兩側(cè)連接的是兩側(cè)道路,長(zhǎng)方形下面的左右兩端點(diǎn)是拱橋兩個(gè)橋墩安裝的位置點(diǎn)。鋼材的彈性模量為E=2.06×105 MPa,泊松比μC=0.3。假設(shè)橋面上承受P=110 MPa 的均布荷載,要求體積減少70%的條件下尋找最合適的拱橋橋型。
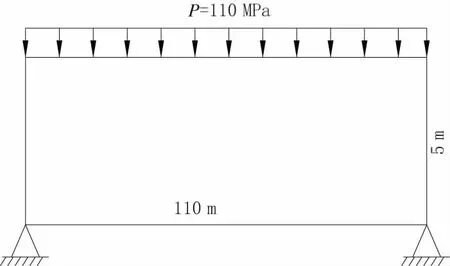
圖1 初始設(shè)定拱橋空間形狀
4.3 設(shè)計(jì)目標(biāo)和約束條件
本例只有一個(gè)荷載工況,屬于單荷載工況求解拓?fù)鋬?yōu)化問(wèn)題,如圖2 所示。首先,將體積減少70%定義為約束函數(shù)。將施加在拱橋頂部的P=110 MPa荷載定義為拓?fù)鋬?yōu)化函數(shù)。該函數(shù)也就是目標(biāo)函數(shù)。

圖2 拱橋截面拓?fù)鋬?yōu)化區(qū)域及有限元模型
4.4 優(yōu)化結(jié)果
由于要尋求拱橋最優(yōu)的結(jié)構(gòu)形式,必須有橋面部分的存在。要求橋面部分為本次研究長(zhǎng)方形的頂部,即長(zhǎng)方形的上表面單元必須保留,不參與拓?fù)鋬?yōu)化迭代過(guò)程。所以,求解時(shí)將長(zhǎng)方形頂層單元指定為非設(shè)計(jì)區(qū)域,其他單元指定為設(shè)計(jì)區(qū)域。
程序通過(guò)七次迭代,以獲得結(jié)構(gòu)最大剛度為最終目標(biāo),并通過(guò)設(shè)計(jì)變量給每個(gè)單元賦予內(nèi)部偽密度來(lái)實(shí)現(xiàn)。
優(yōu)化第一階段,體積減小10%時(shí),優(yōu)化結(jié)果如圖3 所示。

圖3 迭代第一步優(yōu)化圖示
優(yōu)化第二階段,體積減小40%時(shí),優(yōu)化結(jié)果如圖4 所示。

圖4 迭代第四步優(yōu)化圖示
優(yōu)化第三階段,體積減小50%時(shí),優(yōu)化結(jié)果如圖5 所示。

圖5 迭代第五步優(yōu)化圖示
優(yōu)化第四階段,體積減小60%時(shí),優(yōu)化結(jié)果如圖6 所示。

圖6 迭代第六步優(yōu)化圖示
優(yōu)化第五階段,體積減小70%時(shí),優(yōu)化結(jié)果如圖7 所示。

圖7 迭代第七步優(yōu)化圖示
通過(guò)五次迭代,當(dāng)體積刪除VS=50%時(shí),拱橋的橋型逐步顯現(xiàn);當(dāng)體積刪除率VS=70%時(shí),能夠清晰地顯示出拱橋的橋型。此時(shí)迭代停止。在開(kāi)始的幾次迭代中,目標(biāo)函數(shù)和體積變化比較明顯,在經(jīng)歷了第16 次迭代后,優(yōu)化結(jié)果趨于穩(wěn)定,如圖8 所示。
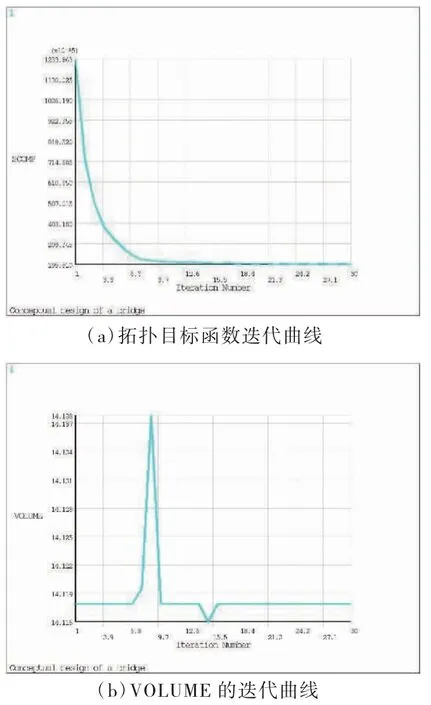
圖8 目標(biāo)函數(shù)、約束函數(shù)的迭代曲線
5 結(jié)語(yǔ)
拓?fù)鋬?yōu)化時(shí),由于尚不明確構(gòu)件尺寸、構(gòu)件之間的連接方式,所以可以利用拓?fù)鋬?yōu)化工具開(kāi)展橋梁結(jié)構(gòu)找型的工作。本文算例是以單元?jiǎng)偠茸畲鬄閮?yōu)化目標(biāo)的二維單元拓?fù)鋬?yōu)化。經(jīng)過(guò)數(shù)次迭代獲得了較成功的拱橋橋型的優(yōu)化結(jié)果,充分證明了采用ESO 法可以很好地開(kāi)展橋梁的找型工作。

