基于多級神經網絡的橋梁結構參數優化設計

姜 群

（杭州市市政工程集團有限公司，浙江 江山 310003）

0 引言

在對橋梁結構進行設計時，對其結構參數的優化，以及通過優化后的參數實現降低建設成本和提升橋梁結構受力性的相關研究，具有十分重要的價值和意義。通過大量學者的研究得出，可通過序列無約束方法結合數值分析對橋梁結構參數進行優化[1]。但這種優化方式在實際應用中得到的優化結果可靠性無法得到保障，因此會進一步影響后續橋梁施工的質量。除此之外，還可通過對不同橋梁結構的正交組合的方式來實現對橋梁結構參數的優化[2]。這種優化方法在實際應用中大大提升了參數優化的效率，但在具體實施過程中，優化的結果會受到采樣階段數據步長變化的影響，因此容易將最優解遺漏，依然無法保證優化參數的可靠性。多級神經網絡技術是一種從單一小網絡開始，通過自動訓練和添加隱藏單元的方式，最終形成多級結構的技術方法。利用該技術在實際應用中能夠有效反映參數變化情況與不同事物性能之間的映射關系，實現對最優性能狀態下參數最優解的獲取[3]。多級神經網絡在實際應用中，能夠有效避免最優解遺漏的產生，進而得到更加可靠的結果。因此，本文結合多級神經網絡的應用優勢，開展對橋梁結構參數優化方法的設計研究。

1 橋梁結構參數優化設計

1.1 構建橋梁結構有限元模型

在明確橋梁結構的相關工程背景和建設需求后，本文采用ANSYS Workbench 17.0 有限元分析軟件，對橋梁結構的有限元模型進行構建。在構建的過程中，需要明確的參數包括建筑材料的彈性模量、材料密度、泊松比等[4]。在實際模型構建時，還應當結合橋梁結構的設計需要，充分考慮預應力鋼束作用，并明確其彈性模量和密度。對于橋梁結構當中的墩頂和橋梁兩端，在構建模型時，默認其固定在端支座上，并受到端支座的約束。為確保在后續對參數進行優化時能夠實現對所有影響問題的全面分析，本文采用四面體網格結構作為橋梁結構有限元模型的基本結構。在完成對模型的構建后，還需要將橋梁整體模型上的節點個數和四面體單元總數進行記錄[5]。本文選取有限元模型中用于優化橋梁結構的主要參數和對應符號，見表1。

表1 有限元模型中優化橋梁結構主要參數和符號

橋梁箱梁寬度d 一般情況下為定值，因此在有序結構參數優化過程中可不將其納入考量范圍。同時，橋梁邊中跨比s 是直接決定橋梁整體剛度的主要因素，因此需要將s 數值作為主要的優化參數變量。橋梁跨中梁高l 和墩頂梁高L 是直接決定橋梁結構承受性的重要因素，因此同樣作為主要的優化參數變量。

1.2 確定橋梁結構參數優化目標

在構建橋梁結構有限元模型，并確定橋梁結構參數優化變量后，設置橋梁結構優化目標函數。通常情況下，在對橋梁結構進行設計時，應當充分考慮到橋梁整體的強度和擾度需求[6]。在滿足上述兩點需求的前提條件下，還應當考慮到在實際建設過程中的經濟性問題。因此，本文確定的橋梁結構參數優化目標函數當中主要包含3 個重要方面，分別為橋梁強度、擾度和經濟性（即橋梁實際施工過程中建筑材料的使用量）。由此可以得出，本文提出的優化目標函數是一個多目標的優化問題，因此引入多級神經網絡，避免在優化過程中出現計算的煩瑣性問題，利用多級神經網絡將多目標轉換為單目標優化問題，得到如式（1）所示的橋梁結構參數多級神經網絡優化目標函數：

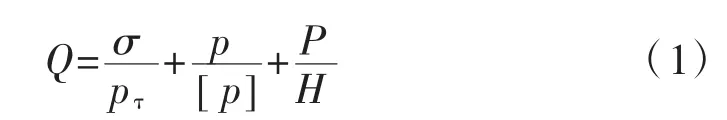
式中：Q 為橋梁結構參數多級神經網絡優化目標結果，即橋梁結構參數應滿足的綜合性能指標；σ 為在極限荷載條件下，橋梁最大承受應力大??；pτ為橋梁建設過程中使用的材料強度極限值；p 為在極限荷載條件下，橋梁主跨跨中位置的撓度值；[ p]為橋梁主跨跨中位置的撓度上限值；P 為按照橋梁建設施工圖紙得出的理論質量；H 為實際工程施工過程中橋梁的總質量。

根據式（1）進行計算，得出在極限荷載條件下某一組橋梁結構參數對應的橋梁最大應力值、跨中位置撓度和橋梁整體的總質量。由此，可進一步求解出不同橋梁結構設計參數下橋梁整體的綜合性能。

1.3 橋梁結構參數優化樣本數據采集

結合基于多級神經網絡確定的橋梁結構參數優化目標，通過對不同橋梁結構參數的隨機匹配，分別計算出橋梁結構綜合性能，再結合均勻設置的方式，得到均勻度良好的參數優化樣本，利用采集到的樣本數據為后續橋梁結構參數多級神經網絡參數優化求解提供數據[7]。通過均勻設置得到的橋梁結構參數優化樣本數據為Wn（qs），其中W 表示均值設置表；n表示樣本數據采集的總次數；q 表示水平系數；s 表示樣本數據采集過程中最多能夠安排的因素系數。通常情況下，根據多級神經網絡的計算需要，水平系數應為因素系數的4 倍，即q=4s。根據上述論述得出，本文參數優化過程中需要因素系數為4，即影響最終橋梁結構參數優化結果的因素包含4 個。由于q=4s，因此本文水平系數應為16 個。在確定不同橋梁結構參數前，還需要對各個參數大致的變化范圍進行設定。按照一般橋梁建設項目的需要，得出以下參數變化范圍設定結果：橋梁邊中跨比s 的變化范圍為0.43~0.67； 橋梁跨中梁高l 的變化范圍為3.57~4.38 m； 橋梁墩頂梁高L 的變化范圍為12.57~12.68 m；橋梁底曲線冪次i 的變化范圍為2.5~3.0。結合差均勻表可得出16 個對應的設計表為W16（1610），在該表當中最多可含有14 個因素，結合W16（1610）的使用表安排方式，將本文上述給出的4個影響因素進行隨機組合，并保證均勻度均滿足要求的情況下完成對橋梁結構參數優化樣本數據的采集。

1.4 橋梁結構參數多級神經網絡參數優化求解

利用多級神經網絡能夠實現對人腦當中大量神經元相互之間連接、處理等操作的模擬。基于這一特點，對橋梁結構參數多級神經網絡參數優化進行求解。首先在多級神經網絡當中引入一定量的數據樣本，進行學習，建立輸入與輸出數據之間的多參數和非線性映射關系[8]。根據多級神經網絡的實際應用效果，設置3 層神經網絡能夠有效實現對橋梁結構參數映射關系的明確。在求解前，需要對上述采集到的樣本數據進行歸一化處理。由于在不同橋梁結構建設和施工過程中，相應的參數量綱不同，因此數值上會存在較大差異。為了有效避免求解過程中，小數據信息內容被大數據信息內容吞噬，需要按照式（2）對所有樣本數據進行歸一化處理：

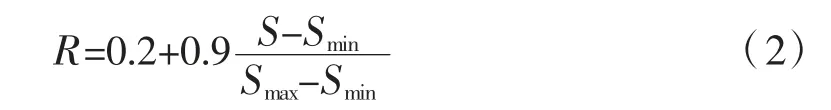
式中：R 為樣本數據歸一化處理后的結果；S 為樣本數據；Smin為每組樣本數據當中的最小值；Smax為每組樣本數據當中的最大值。按照式（2）進行歸一化處理后，將所有得到的輸入數據和輸出數據全部規劃到[0.2~0.8]區間范圍以內。因此，通過上述操作，既能夠有效保留原有樣本數據當中的相對信息量，也能夠實現對多級神經網絡學習速度和收斂能力的提升。

在橋梁結構參數多級神經網絡參數優化求解過程中，還需要對神經網絡中的隱藏層計算結果進行確定[9]。在計算時，隱藏層當中的樣本數據量過少會嚴重影響求解時非線性網絡逼近的精度，進而影響參數優化的最終效果。因此，根據式（3）對多級神經網絡隱含層當中的樣本數據個數進行確定：

式中：e 為多級神經網絡隱含層當中包含的樣本數據個數；i 為多級神經網絡輸入層當中的樣本數據個數；j 為多級神經網絡輸出層當中的樣本數據個數；a為[1，10]范圍內的正整數。根據式（3）計算，得出的e值在滿足非線性網絡逼近的精度條件下，才能夠按照本文上述論述完成對橋梁結構參數的優化求解[10]。若e 值不滿足非線性網絡逼近的精度條件，則需要重新對樣本數據進行采集，并重新規劃各個參數變量的變化范圍，直到e 值滿足精度條件后，才能帶入式（1）、式（2），完成對橋梁結構參數的優化。

2 對比實驗

某地區大跨預應力橋梁結構整體采用150 m+210 m+150 m 跨度，整體結構上以單箱單室預應力混凝體材料現澆箱梁為主。橋梁墩頂截面高度為12 m，寬度為13.5 ，跨中截面高度為11.25 m，寬度為3.5 m。為驗證本文提出的基于多級神經網絡的橋梁結構參數優化方法的有效性，將該橋梁結構作為實驗對象，分別利用本文參數優化方法和傳統參數優化方法，對該橋梁結構參數進行優化設計。為保證實驗結果的客觀性，兩種優化方法均利用本文上述提出的4個參數變量作為一般參數。設置一般參數為：[橋梁邊中跨比s，橋梁跨中梁高l，橋梁墩頂梁高L，橋梁底曲線冪次i]T=[0.427，13.548，2.584，2.018]T。在上述規定參數狀態下，對比兩種參數優化方法優化后的橋梁結構綜合性能，以此對比兩種參數優化方法的實際應用效果。為方便實驗結果進行比較，利用式（1）對參數優化后的橋梁結構整體性能進行量化得出Q 值（Q 值應小于4），將計算結果進行記錄，并繪制成如表2 所示的實驗結果對比表。

表2 兩種參數優化方法實驗結果對比

從表2 的實驗結果可以看出，隨著優化次數的不斷增加，本文參數優化方法和傳統參數優化方法得出的Q 值均呈現出上升趨勢，但明顯本文優化方法Q 值上升更快。對兩種參數優化方法橫向比較能夠進一步看出，本文每次優化后的Q 值均明顯高于傳統參數優化方法的Q 值。Q 值越高，說明橋梁結構整體性能越高。因此，通過實驗進一步得出，本文提出的基于多級神經網絡的橋梁結構參數優化方法在實際應用中能夠有效提高橋梁結構整體性能，實現更加有效的參數優化。

3 結語

為實現對橋梁結構整體性能的提升，針對橋梁結構參數優化過程中存在的普遍性問題，結合多級神經網絡，提出一種全新的參數優化方法。將本文提出的參數優化方法應用于實際能夠有效實現對橋梁結構整體性能的提高，同時能夠為橋梁實際施工過程中產生的各類問題提供所需的數據條件，以此為進一步實現橋梁建設施工的高質量發展提供有力的數據支撐。