融合切線段的hRRT 狹窄空間路徑規劃算法

周飛龍，甘 屹

（上海理工大學機械工程學院，上海 200093）

0 引言

相對于其他算法，RRT 算法因其在多約束、高維路徑規劃問題中具有概率完備性和漸近最優性［13］而越來越受歡迎。針對RRT 算法收斂速度較慢的問題，Urmson 等［14］更改節點采樣方式，提出具有節點偏向目標概率的hRRT（Heuristically RRT）算法；Wang［15］從多隨機樹方面提出雙向隨機樹；劉成菊等［16］提出基于RRT 的變步長搜索以提高搜索效率。

路徑規劃算法的目的是找到可達路徑，然而一些基于RRT 的算法在狹窄復雜環境中并不能求解出路徑。這是由于在狹窄空間中選取節點是困難的，狹窄通道體積小，任何基于容量的抽樣分布都可能失敗［17］。Rodriguez 等［18］從多向隨機樹角度提出了在OB-RRT（Obstacle Based RRT）中通過狹窄通道區域建立根節點，讓隨機樹更快地尋找到可行路徑，但需要預先確定狹窄空間位置；Informed-RRT*與RABIT*通過局部優化器，提高路徑中的狹窄區域采樣概率，但是其效率有待提高［19-20］；文獻［13］提供一種橋梁檢測算法提高對狹窄空間的采樣概率，但會在有凹三角形輪廓障礙物附近產生多余采樣節點，增加了算法時間。

本文提出一種融合切線段的hRRT 狹窄空間路徑規劃算法（An hRRT Narrow Space Path Planning Algorithm Fused with Tangent Segment，T-hRRT）。先使用hRRT 算法搜索到障礙物附近，再利用切線段尋找狹窄空間入口并構建障礙物輪廓的可通過狹窄空間，由于最短路徑的解一定是由切線及其輪廓組成［8］，因此，T-hRRT 算法在狹窄空間環境中可以得到相對較短的路徑，并且算法效率大幅提高。

1 狹窄空間定義

全局通行度是在地圖上的所有可通行空間內，除去機器人或車輛所占空間外，自由空間面積的最小值與該點自由空間總面積的百分比［21］。在二維的管道與洞穴環境中，將自由空間面積轉化為水平截面寬度化簡計算，如式（1）所示。

式（1）中，p為全局通行度，wmin為全局地圖可通行的自由空間的最小水平截面寬度，wrobot為移動機器人寬度。當p>0 時，機器人能從狹窄通道通過，當p≤0 時，該路段不可通行。本文將通行度為50% 以下的空間定義為狹窄空間，50%以上的稱為普通空間。本文主要以狹窄空間為基礎對hRRT 路徑規劃算法進行研究。

2 hRRT 算法原理

hRRT 算法優先向目標方向擴展低代價路徑，同時保持對探索的合理偏向。hRRT 算法以起始點qstɑrt作為隨機樹RRTree 的根節點。按照特定概率函數F 從自由空間Sfree中選擇隨機點qrɑnd或者目標點qgoɑl作為采樣點qsɑmple。在隨機樹RRTree 中尋找距離采樣點qsɑmple最近的節點qneɑr，以節點qneɑr為原點向采樣點qsɑmple方向延長步長ε獲得新節點qnew。若新節點qnew路徑未經過障礙物空間Sobs，則將新節點qnew加入隨機樹RRTree 中，若經過障礙物空間Sobs，則搜索失敗，重新選取采樣點qsɑmple。當樹中的節點擴散到目標點qgoɑl時，完成整個搜索，返回起始點qstɑrt到目標點qgoɑl的路徑節點，hRRT 算法原理如圖1 所示。

我們來梳理一下這三個步驟，第一步通過寫作建立人物形象，這是“以寫促讀”；第二步對照原文修改寫作片段，這是“以讀促寫”；第三步學習聯想，用聯想的方法再次修改寫作片段，這又是“以讀促寫”。在不斷修改的過程中，加深學生對“全神貫注”一詞及文章主旨的認識。

hRRT 算法采用啟發式成本低的目標偏置節點進行擴展，縮短計算時間，但是當環境中存在狹窄通道時，其性能會出現大幅度下降。其原因主要是由于hRRT 算法采用基于概率函數的隨機采樣策略，相對于整個環境空間而言，窄道所占面積比例很小，導致窄道內采樣概率很低，隨機樹難以在狹窄通道中擴展，從而狹窄通道兩端無法連通，最終導致路徑無解。

Fig.1 Schematic diagram of hRRT algorithm principle圖1 hRRT 算法原理示意圖

3 融合切線段的hRRT 路徑規劃算法

切線算法基于障礙物邊緣間的切線構成最短無碰撞路徑原理，應用Dijkstra 算法遍歷所有障礙物切點，在二維地圖中能得到最短路徑，并且其環境適應性好，在狹窄通道環境中也能搜索到最短路徑。缺點是時間復雜度與空間復雜度較高，隨著地圖中障礙物切點數目的增多，算法搜索效率逐漸下降。

本文采用hRRT 算法與切線算法相結合的方法，利用hRRT 算法避免切線算法的全局搜索，利用切線算法通過狹窄通道，加快路徑搜索速度，兩者相輔相成。

3.1 地圖柵格化

任意地圖環境都可以被量化成具有一定分辨率的柵格，而柵格大小直接影響信息存儲量的大小和建模精度兩個問題［21］。由于原始地圖信息過大，切線算法時間和空間復雜度較高，為了提高效率、降低資源占用，本文使用柵格法進行環境建模，簡化地圖。

對于狹窄空間，較大的障礙柵格尺寸會使通路變得更窄，甚至使通路封閉而影響結果，而較小的柵格尺寸會增加算法計算量。因此設計合理的柵格大小很重要，本文定義柵格化尺度為移動機器人體積的一半，保證地圖狹窄通道的原有信息，又減少了計算量，如式（2）所示。

式（3）中，Gxy為柵格取值，1 為障礙柵格，0 為自由柵格；glimit為柵格劃分閾值，當附近的障礙面積大于此值，代表此柵格為障礙物點。式（4）中，g(x,y)為原始地圖(x,y)處的值，障礙空間數值為1，自由空間數值為0；∑gɑround為柵格點附近原始地圖中的取值之和，代表了附近柵格的障礙面積。

3.2 障礙物凸點檢測

地圖中任意障礙物經過柵格化處理可以形成多邊形模型，自由空間Sfree內任意一點與障礙物多邊形模型的切點一定在其凸點［8］。如圖2 所示，黑色區域為障礙物柵格化后的多邊形模型，紅色點為障礙物多邊形模型的凸點（彩圖掃OSID 碼可見）。

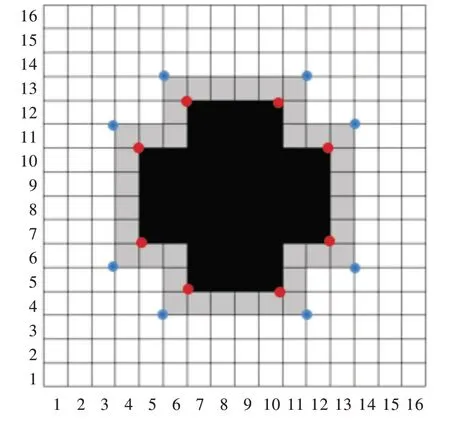
Fig.2 Rasterized maps圖2 柵格化地圖

因為路徑規劃時將移動機器人設為質點，但機器人體積不可忽略，故需要在障礙物周圍設置安全距離dsɑfe。本文設置的安全距離為障礙物向外一個柵格的距離，即dsɑfe=，如圖2 所示的灰色區域內為移動機器人碰撞區域，在移動機器人運動過程中需要避開該區域。

針對安全距離問題，如圖2 所示，將灰色包圍區域作為最終障礙物模型，使用藍色凸點作為本文規劃算法中所使用的凸點，從而保證算法能夠規劃出一條無碰撞路徑。搜索地圖環境中所有凸點，將凸點位置信息放入凸點矩陣bumps{[xi yi]}。凸點檢測的偽代碼如下：

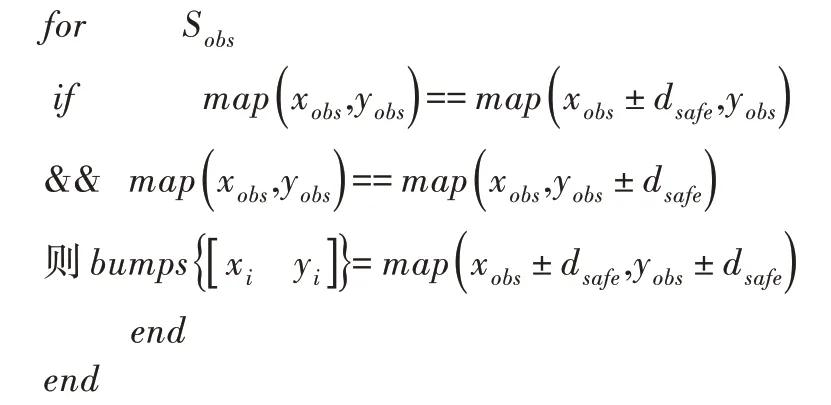
3.3 切點搜索

在搜索切點時，本文通過有限長度的切線段搜索切點。連接自由空間任意一點xfree與所有凸點，并且兩端延長e=wrobot，如果生成的線段中沒有經過障礙物空間，則該生成線段的凸點為xfree對障礙物模型的切點。如圖3 所示，A點為xfree對障礙物模型的一個切點，用來尋找狹窄空間入口處的節點。

根據上述方法，還可以規劃障礙物模型輪廓路徑，如圖3 所示，以障礙物模型上的凸點A 為原點搜索切點，點B滿足要求。A、B 兩點連接構成障礙物模型的一段輪廓路徑，確保隨機樹在狹窄空間中有效擴展，切點搜索偽代碼如下：

對于有公切線的障礙物，切線段會多次往復搜索，陷入局部收斂。本文將重復的切點只在RRTree 中記錄一次，減少隨機樹節點數，并且使得算法快速跳出局部收斂。

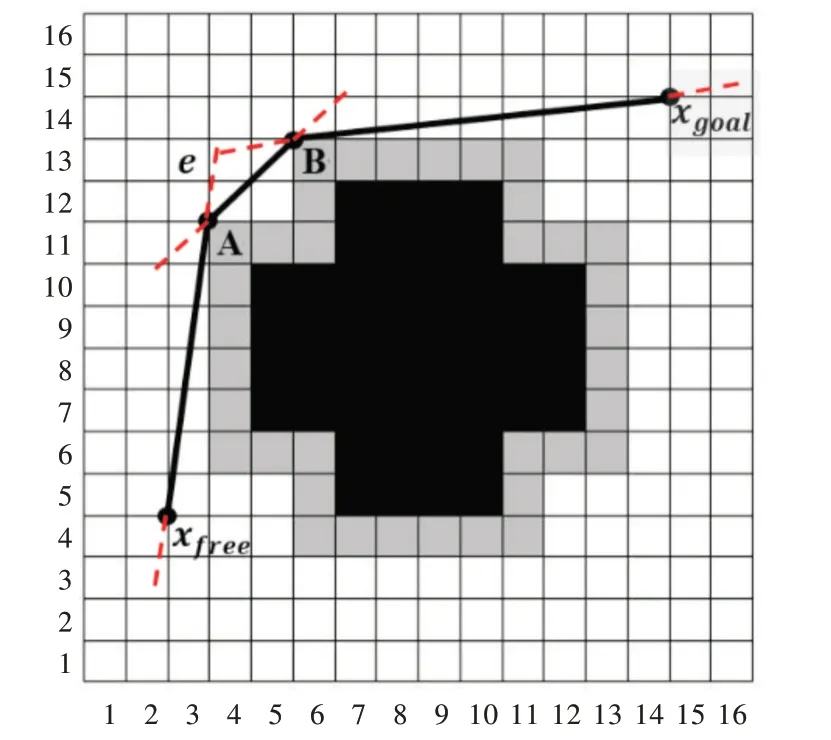
Fig.3 Tangent section of point to obstacle圖3 點對障礙物切線段

3.4 算法實現

算法實現過程如下：

Step1：輸入起始點qstɑrt、目標點qgoɑl、地圖環境的信息。

Step2：柵格化地圖，并查找地圖中障礙物凸點bumps。

Step3：設置概率函數，本文采用簡單概率函數F，利用函數在0 到1 區間隨機取值，當大于0.5 時，進入隨機采樣，當小于等于0.5 時，偏向目標采樣。

Step4：尋找隨機樹RRTree 中距離采樣點qsɑmple最近的點qneɑr，按照采樣點qsɑmple方向定步長ε擴展生成新節點qnew，判斷該路徑間是否有障礙，若存在障礙，則進入Step5，若無障礙，將新節點qnew加入到隨機樹中RRTree。

Step5：以當前距離采樣點qsɑmple最近的點qneɑr做障礙物切線段，將切點加入隨機樹RRTree 中，刪除重復切點。

Step6：當隨機樹中的節點與目標點qgoɑl沒有障礙時，路徑搜索完成。

4 實驗分析

為了驗證T-hRRT 路徑規劃算法性能，本文在3 種地圖環境中對hRRT 算法、切線算法以及T-hRRT 算法進行仿真，地圖中黑色幾何圖形代表障礙物，空白區域為自由空間，藍色細短線表示分支，黑色粗線表示最終生成的路徑。算法運行環境為：64bit Windows10 操作系統；MATLAB 2019a；處理Intel（R）Core（TM）i5-9300H；主頻2.4GHz；內存8GB。

4.1 普通空間環境

地圖一為普通空間環境，大小為500*500 分辨率，全局通行度大于50%，起始點與目標點位置分布為（10，10）與（490，490）。該地圖用于驗證3 種算法在起點與終點之間包含多障礙物時的搜索能力，如圖4（a）、4（b）、4（c）分別為切線算法、hRRT 算法、T-hRRT 算法在地圖一環境下的一次實驗結果，其中hRRT 算法的步長為30。

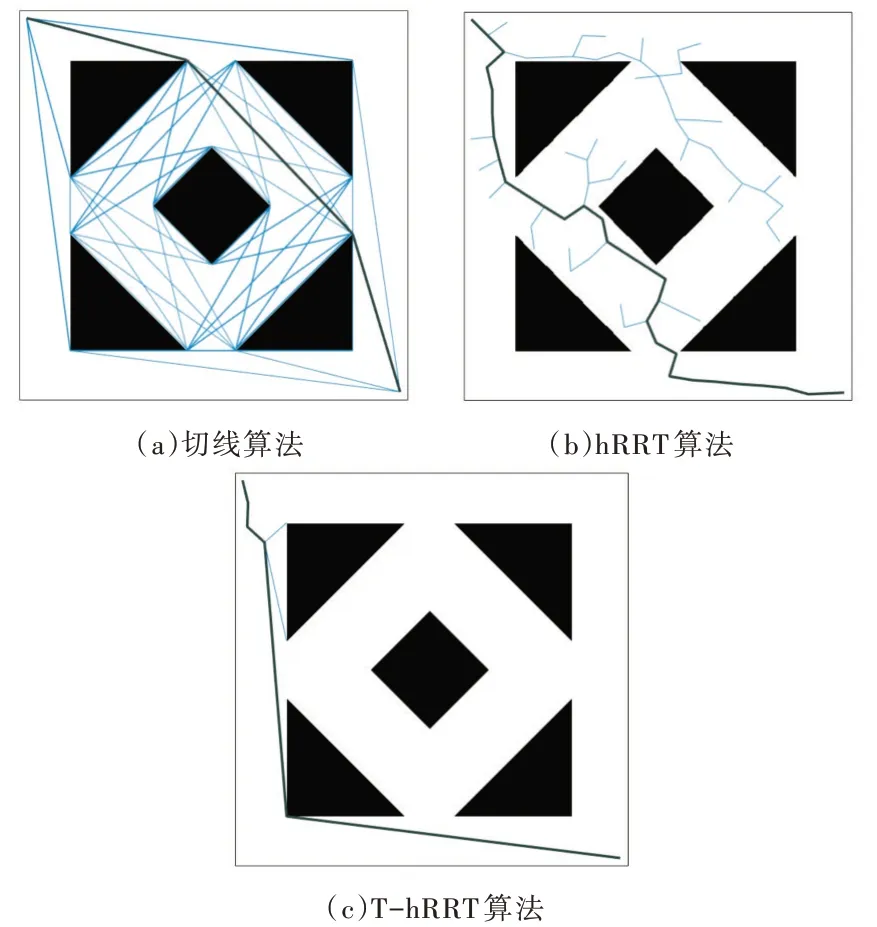
Fig.4 Results of map 1 experiment圖4 地圖一中實驗結果

在地圖一普通空間環境中對3 種算法經過20 次試驗，其規劃時間、路徑長度與節點數如表1 所示。

Table 1 Simulation results of three algorithms in ordinary space environment表1 普通空間環境下3 種算法仿真結果

由表1 可知，在地圖一環境中T-hRRT 算法獲得相對于hRRT 算法的較短路徑，平均節點數減少了87%，搜索時間減少了90%；相對于切線算法減少了99%的平均規劃時間。結果表明，T-hRRT 算法在普通空間環境中表現良好。

4.2 狹窄空間環境

地圖二與地圖三為狹窄空間環境，大小為500*500 分辨率，全局通行度小于50%，其中地圖二只為直線型狹窄空間環境，地圖三為不規則輪廓型狹窄空間環境。起始點與目標點位置分布為（10，10）與（490，490）。用于驗證3 種算法在起點與終點之間包含不同狹窄空間時的搜索能力，圖5（a）、5（b）、5（c）、6（a）、6（b）、6（c）為兩種狹窄空間環境中切線算法、hRRT 算法、T-hRRT 算法的一次實驗結果。

在地圖二直線型狹窄空間環境與地圖三不規則輪廓型狹窄空間環境中對3 種算法經過20 次試驗，其規劃時間、路徑長度與節點數如表2 和表3 所示。

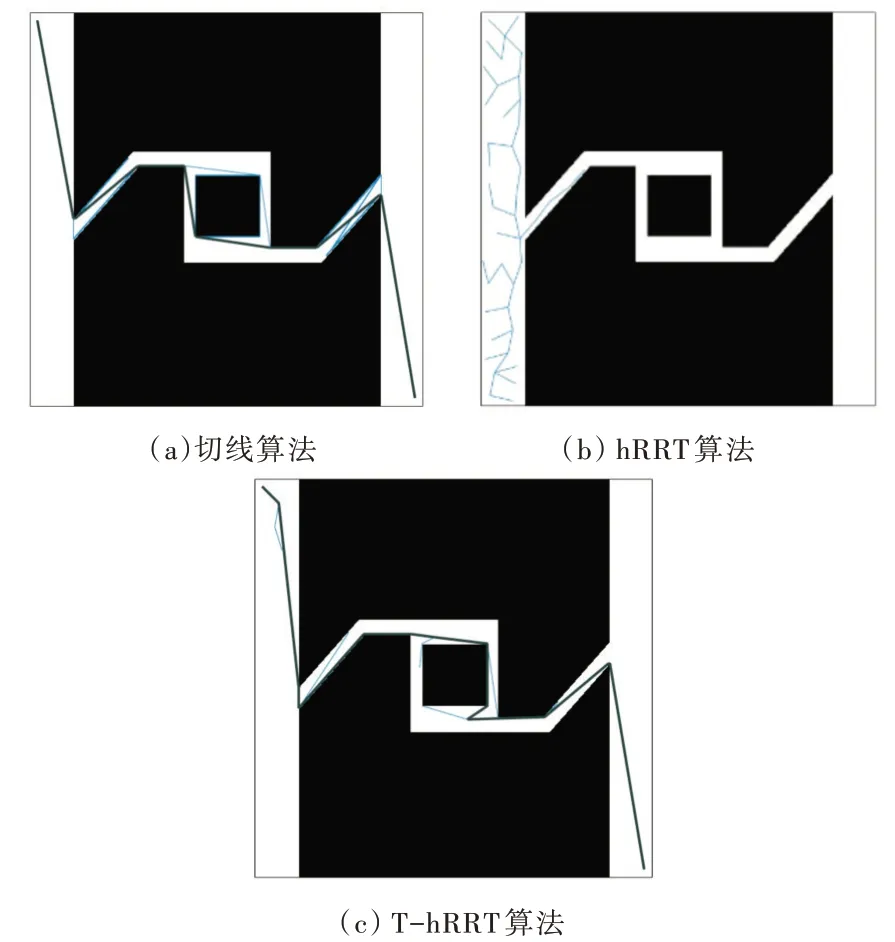
Fig.5 Results of map 2 experiment圖5 地圖二中實驗結果

Fig.6 Results of map 3 experiment圖6 地圖三中實驗結果

Table 2 Simulation results of three algorithms under linear narrow space environment表2 直線型狹窄空間環境下3 種算法仿真結果

表2 與表3 中的值為無窮，表示該算法在此環境中失效，而對于切線算法無節點數，步長為30 的hRRT 算法在地圖二與地圖三狹窄空間環境中失效，顯然狹窄環境影響了隨機樹的有效擴展，達到節點最大搜索次數時無解。切線算法與T-hRRT 算法都能通過狹窄通道，但是T-hRRT 算法在地圖二直線型狹窄空間環境與地圖三不規則輪廓型狹窄空間環境中平均規劃時間相比于切線算法減少了89%，而平均路徑長度不超過切線算法規劃最短路徑長度的5%。

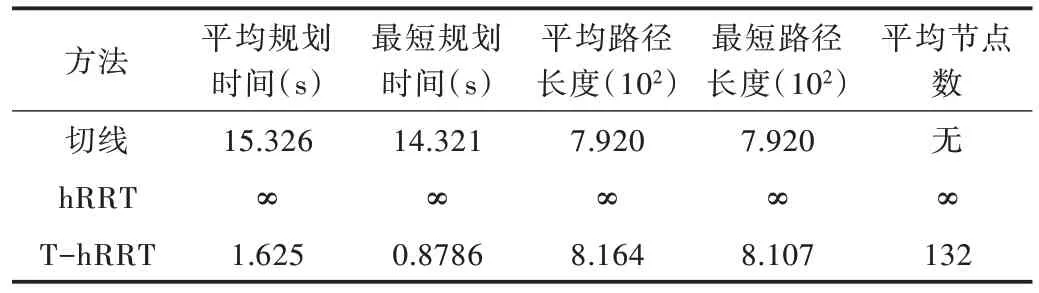
Table 3 Simulation results of three algorithms in narrow space with irregular contour表3 不規則輪廓型狹窄空間環境下3 種算法仿真結果

5 結語

針對狹窄空間下hRRT 算法路徑無解問題，本文結合切線算法與hRRT 算法，提出T-hRRT 算法，利用切線算法加快hRRT 算法節點擴展與通過狹窄空間，利用hRRT 算法隨機擴展節點避免切線算法的全局計算，相互彌補缺點從而獲得規劃時間較少并且長度較短的路徑。T-hRRT 算法完成了hRRT 算法不能解決的狹窄通道問題，并且其路徑長度與切線算法規劃的最短路徑長度相差不到5%，而相對于切線算法的規劃時間減少了約89%。在后續研究中，將進一步提升算法在三維空間與未知、動態環境中的規劃能力。