基于萊維飛行的改進(jìn)簡(jiǎn)化粒子群算法

梁 田，曹德欣

中國礦業(yè)大學(xué) 數(shù)學(xué)學(xué)院，江蘇 徐州 221116

粒子群優(yōu)化算法（Particle Swarm Optimization，PSO）是基于群體的啟發(fā)式優(yōu)化算法，由Kennedy和Eberhart[1]于20世紀(jì)90年代首次提出。通過模擬鳥類捕食行為來構(gòu)建優(yōu)化算法。每個(gè)個(gè)體都被稱作是一個(gè)粒子，算法通過粒子之間的群體協(xié)作使其達(dá)到最優(yōu)。與其他復(fù)雜智能算法不同，PSO算法原理簡(jiǎn)單，沒有交叉、變異等復(fù)雜的操作。故在經(jīng)濟(jì)管理、信息科學(xué)、工程技術(shù)、函數(shù)優(yōu)化等諸多領(lǐng)域中應(yīng)用廣泛。

但PSO算法參數(shù)固定，對(duì)復(fù)雜函數(shù)進(jìn)行優(yōu)化時(shí)表現(xiàn)出較差的求解精度。雖然算法在前期若干次迭代效果尚好，但后期易陷入局部最優(yōu)。因此，對(duì)基本PSO算法的改進(jìn)成為國內(nèi)外學(xué)者研究的焦點(diǎn)。Shi等在文獻(xiàn)[2]中初次提出慣性權(quán)重概念，文中將慣性權(quán)重的取值從0.9線性遞減至0.4，算法性能得到明顯的改善。Kennedy等[3]分析粒子間的信息流，提出一系列的拓?fù)浣Y(jié)構(gòu)。高立群等[4]在粒子群算法中加入變異因子，在粒子速度和位置更新之后進(jìn)行變異操作。以上對(duì)基本PSO算法的改進(jìn)可有效地避免算法的參數(shù)固定、粒子種群多樣性減少等不足，改善其收斂性能。

上述改進(jìn)算法雖在性能上有所改善，但早熟收斂現(xiàn)象仍然存在。為能更好改善基本PSO算法的尋優(yōu)性能，提出一種基于萊維飛行的改進(jìn)簡(jiǎn)化粒子群算法（LISPSO）。首先，將帶有隨機(jī)性的非線性遞減慣性權(quán)重引入到簡(jiǎn)化PSO上。前期的慣性權(quán)重值較大，全局搜索能力強(qiáng)。而后期取值較小能夠提高算法局部搜索能力。其次，為保證粒子逃離局部最優(yōu)，該算法融入基于相似度及聚集度分析的萊維飛行。利用粒子與最優(yōu)粒子之間的歐氏距離來定義粒子與最優(yōu)粒子間的相似度，同時(shí)利用粒子與最優(yōu)粒子的平均相似度計(jì)算粒子群的聚集度。粒子間的相似度或者聚集度越大，則粒子進(jìn)行萊維飛行的概率就越大。保持粒子種群多樣性，避免算法早熟收斂。

1 標(biāo)準(zhǔn)粒子群優(yōu)化算法NPSO（Normative Paticle Swarm Optimization）

PSO算法從隨機(jī)解出發(fā)，通過不斷迭代尋求最優(yōu)解或近似最優(yōu)解，通常用于解決各類優(yōu)化問題。在PSO算法模型中，每個(gè)粒子代表優(yōu)化問題在搜索空間的潛在解。首先，算法初始化每個(gè)粒子，它們都有自己相對(duì)應(yīng)的初始速度和位置。其次，算法每進(jìn)行一次更新，粒子都通過追蹤目前自身找到的最優(yōu)位置（個(gè)體極值）和所有粒子搜索到的最優(yōu)位置（全局極值）來重新調(diào)整自身的狀態(tài)。另外，每個(gè)粒子都有其對(duì)應(yīng)的適應(yīng)度函數(shù)值，由此來評(píng)判該粒子所在位置的優(yōu)劣。

可用d維向量來表示所有粒子的位置和速度，即：

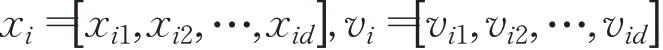
每次迭代，粒子速度及位置更新公式如下：

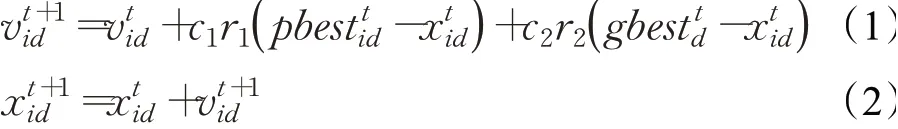
在式（1）和（2）中，t表示當(dāng)前進(jìn)化代數(shù)；c1、c2為學(xué)習(xí)因子，一般取值為2；r1、r2為()0,1之間相互獨(dú)立的隨機(jī)數(shù)；在文獻(xiàn)[2]中，Shi和Eberhart提出慣性權(quán)重w，后來他們又給出線性遞減慣性權(quán)重：

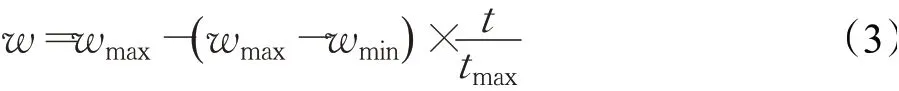
速度更新公式（1）進(jìn)一步修改為：

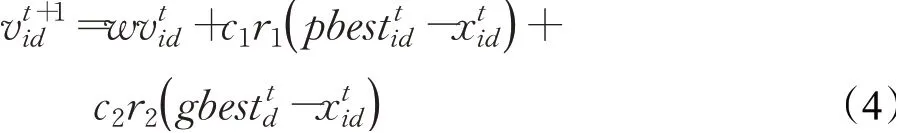
其中，wmax和wmin分別表示慣性權(quán)重最大值和最小值，通常取值為0.9和0.4。tmax代表最大迭代次數(shù)，t表示當(dāng)前迭代次數(shù)。一般稱上述算法為標(biāo)準(zhǔn)粒子群算法（NPSO）。

2 基于萊維飛行的改進(jìn)簡(jiǎn)化粒子群算法（LISPSO）

2.1 預(yù)備知識(shí)介紹

2.1.1 簡(jiǎn)化粒子群優(yōu)化算法（SPSO）

粒子速度過于發(fā)散會(huì)導(dǎo)致后期收斂速度慢，為了解決此問題，文獻(xiàn)[5]提出了一種簡(jiǎn)化粒子群算法。該算法舍去了速度項(xiàng)，僅由粒子的位置項(xiàng)控制粒子的進(jìn)化方向。標(biāo)準(zhǔn)粒子群算法中公式（2）和（4）簡(jiǎn)化為：

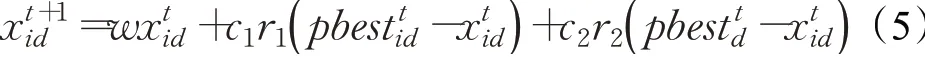
式中，c1、c2一般取值均為2，文獻(xiàn)[5]中w取值0.8。

2.1.2 萊維飛行

萊維飛行是服從萊維分布的短距離和偶爾較長(zhǎng)距離行走相間的一種隨機(jī)搜索路徑。經(jīng)大量研究，它符合蜜蜂和果蠅等自然界的許多動(dòng)物昆蟲的覓食軌跡[6]。目前萊維飛行在優(yōu)化領(lǐng)域應(yīng)用廣泛，如王慶喜等在文獻(xiàn)[7]中提出若算法陷入局部最優(yōu)，則用萊維飛行公式重新調(diào)整粒子的位置。劉曉龍等利用萊維飛行改進(jìn)鳥群算法[8]。萊維飛行的位置更新方程為：

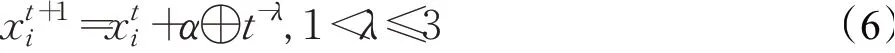
式中，i∈[1,2,…,N],表示第i個(gè)粒子在第t次迭代時(shí)的位置；⊕為點(diǎn)對(duì)點(diǎn)乘法；α代表步長(zhǎng)控制量。

萊維飛行的步長(zhǎng)符合萊維分布，常使用Mantegna算法模擬，步長(zhǎng)s計(jì)算公式：

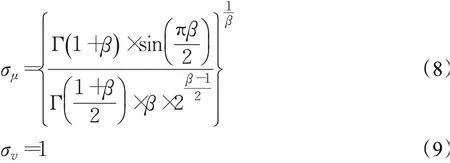
β通常取值1.5。

2.2 算法改進(jìn)

2.2.1 帶有隨機(jī)性的非線性遞減慣性權(quán)重

在PSO算法中，慣性權(quán)重取值大利于算法進(jìn)行更廣泛的搜索，小的慣性權(quán)重值則能夠提高算法精準(zhǔn)的局部搜索能力。因此，慣性權(quán)重的取值至關(guān)重要。基于此，提出帶有隨機(jī)性的非線性遞減慣性權(quán)重，該慣性權(quán)重如下：

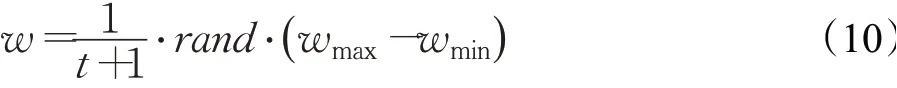
式中，t表示當(dāng)前迭代次數(shù)，rand為(0,1)之間的隨機(jī)數(shù)。wmax和wmin分別表示慣性權(quán)重的最大值和最小值。

慣性權(quán)重w在()0,1之間取值，迭代次數(shù)增加，慣性權(quán)重取值非線性地逐漸減小。另外，為了避免種群多樣性減少，文獻(xiàn)[9]給出反向搜索策略，即算法每次迭代都要根據(jù)隨機(jī)數(shù)的取值來決定是否進(jìn)行反向搜索。本文引入文獻(xiàn)[9]的反向搜索機(jī)制y()r。其計(jì)算公式為：

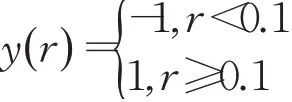
則改進(jìn)后的簡(jiǎn)化粒子群算法的迭代公式由式（5）修改如下：

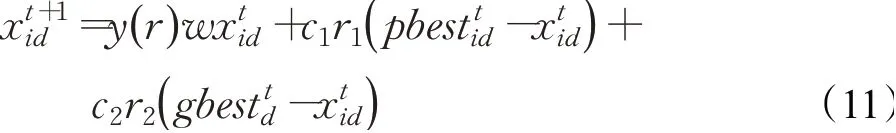
其中，r為()0,1之間的隨機(jī)數(shù)，式（11）中的w按照式（10）進(jìn)行更新。

2.2.2 粒子群的相似度及聚集度

隨著迭代次數(shù)的增加，粒子最終都會(huì)向最優(yōu)粒子靠攏[10-11]。靠攏過程中，粒子間距隨之縮小，相似度隨之增大。現(xiàn)將粒子間的相似度定義如下：

其中，s(i,j)代表粒子i與粒子j之間的相似度；d(i,j)表示粒子i和粒子j的歐式距離；dmax表示粒子間所有距離的最大值。

從公式（12）可以看出，粒子間的相似度在()0,1之間取值，且兩個(gè)粒子之間的相似度隨著距離的增大而減小。當(dāng)d(i,j)→0時(shí)，s(i,j)→1，說明兩個(gè)粒子很相似。反之，當(dāng)d(i,j)→∞時(shí)，s(i,j)→0，說明兩個(gè)粒子幾乎不相似。

在PSO算法迭代過程中會(huì)出現(xiàn)粒子聚集現(xiàn)象。文獻(xiàn)[12]給出聚集度的定義以及計(jì)算公式，將每個(gè)粒子與當(dāng)前代最優(yōu)粒子的平均相似度作為粒子群的聚集度。聚集度越高，粒子種群多樣性越低。本文采用文獻(xiàn)[11]的聚集度計(jì)算方法，即：

其中，N代表粒子群數(shù)，s(i,g)為粒子i與當(dāng)前最優(yōu)粒子g的相似度，c(t)表示第t代粒子群的聚集度。

2.2.3 基于相似度及聚集度分析的萊維飛行

由2.2.2小節(jié)得到粒子群相似度及聚集度的計(jì)算方法。用相似度來衡量?jī)蓚€(gè)粒子的間距，而聚集度則量化粒子群多樣性。

若所有粒子都聚集在目前最優(yōu)粒子p g附近，算法會(huì)隨著迭代的進(jìn)行而出現(xiàn)停滯。若目前的p g是局部最優(yōu)點(diǎn)，那么此時(shí)得到的解并非全局最優(yōu)解。為使粒子逃離局部最優(yōu)，提高種群多樣性，對(duì)其進(jìn)行萊維飛行，以此來重新更新粒子的位置。

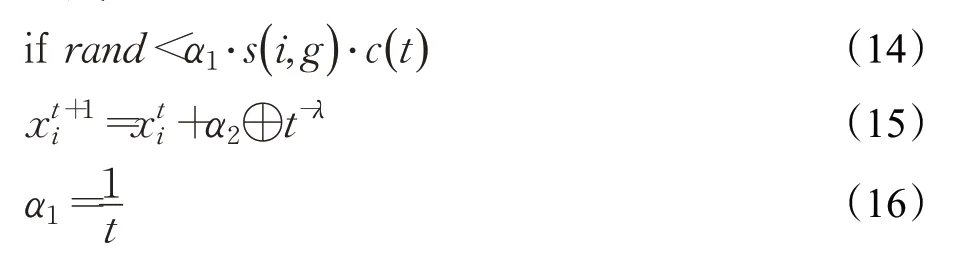
其中，1<λ≤3，參數(shù)α1為一個(gè)關(guān)于迭代次數(shù)的非線性遞減函數(shù)。α2為步長(zhǎng)控制量，是一固定常數(shù)，經(jīng)過大量實(shí)驗(yàn)，當(dāng)α2=0.01時(shí)，算法的數(shù)值實(shí)驗(yàn)效果較好；rand為(0,1)之間的隨機(jī)數(shù)。

分析式（14）、（15），s(i,g)越大，或者c(t)越大，粒子利用萊維飛行來重新更新自己位置的可能性也就越大，利于粒子快速逃離局部最優(yōu)。

2.3 LISPSO算法

綜合2.2節(jié)的分析，提出基于萊維飛行的改進(jìn)簡(jiǎn)化粒子群算法（LISPSO）。算法步驟如下：

步驟1對(duì)粒子的位置進(jìn)行初始化處理，并設(shè)置相關(guān)參數(shù)：種群規(guī)模N；學(xué)習(xí)因子c1、c2；最大迭代次數(shù)M等。

步驟2計(jì)算每個(gè)粒子適應(yīng)度值，并將適應(yīng)度值進(jìn)行比較、替換，記錄全局最優(yōu)值和個(gè)體最優(yōu)值。

步驟3分別按照公式（10）、（11）更新粒子的慣性權(quán)重值及粒子的位置。

步驟4重新調(diào)整粒子的個(gè)體最優(yōu)值及全局最優(yōu)值。

步驟5根據(jù)公式（12）、（13）計(jì)算s(i,g)和c(t)，并利用式（14）、（15）判斷粒子是否進(jìn)行萊維飛行。若粒子進(jìn)行萊維飛行，則返回步驟4；否則，進(jìn)行步驟6。

步驟6記錄當(dāng)前全局最優(yōu)值。

步驟7判斷算法是否滿足迭代搜索條件，若滿足，則算法終止；否則，算法轉(zhuǎn)至步驟3。

3 LISPSO算法的時(shí)間復(fù)雜度分析

在基本粒子群算法中，假設(shè)位置自變量維數(shù)為d，種群大小為n。初始化階段，各參數(shù)初始值的設(shè)置、粒子隨機(jī)生成初始速度和位置、生成隨機(jī)數(shù)、計(jì)算粒子適應(yīng)度值以及將所有個(gè)體適應(yīng)度值進(jìn)行排序得到最優(yōu)個(gè)體適應(yīng)度值的時(shí)間分別為t1、t2、t3、f()d以及t4。則初始化階段總體時(shí)間復(fù)雜度為：

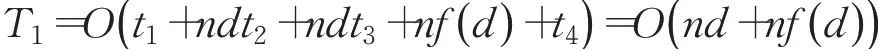
設(shè)迭代階段的迭代次數(shù)為m，粒子個(gè)體每一維進(jìn)行位置和速度更新所花費(fèi)的時(shí)間分別為t5和t6。則該階段的時(shí)間復(fù)雜度為：

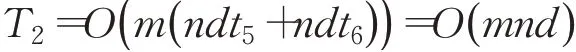
每個(gè)粒子在更新位置和速度之后，都會(huì)重新計(jì)算其適應(yīng)值并將它們進(jìn)行比較、替換。在記錄最優(yōu)解階段，設(shè)重新計(jì)算更新位置和速度后的粒子適應(yīng)值以及每個(gè)個(gè)體適應(yīng)度值與當(dāng)前最優(yōu)解進(jìn)行比較、替換的時(shí)間分別為f(d)和t7，那么該階段的時(shí)間復(fù)雜度為：

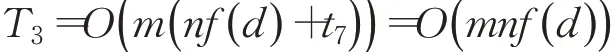
最后判斷算法是否達(dá)到迭代終止條件，設(shè)所花費(fèi)時(shí)間為t8，那么該階段的時(shí)間復(fù)雜度為：

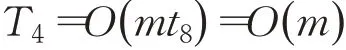
綜上所述，基本粒子群算法的時(shí)間復(fù)雜度為：

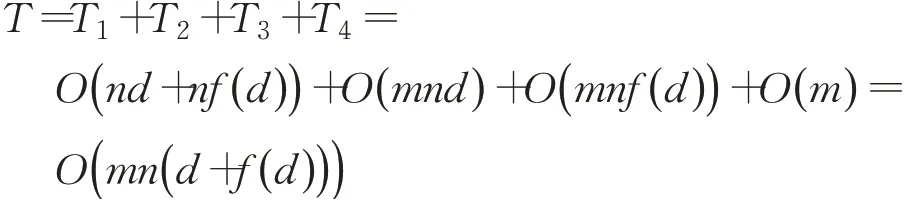
LISPSO算法在基本粒子群算法的基礎(chǔ)上增加了帶有隨機(jī)性的非線性遞減慣性權(quán)重、反向搜索機(jī)制、相似度及聚集度。設(shè)系統(tǒng)計(jì)算慣性權(quán)重w的時(shí)間為g1，判斷粒子是否進(jìn)行反向搜索所需要的時(shí)間為g2，計(jì)算粒子與最優(yōu)粒子的相似度以及每一代粒子的聚集度所花費(fèi)的時(shí)間分別為g3和g4。則計(jì)算非線性慣性權(quán)重、反向搜索機(jī)制、相似度及聚集度所產(chǎn)生的時(shí)間復(fù)雜度為：

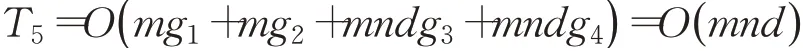
從而LISPSO算法的時(shí)間復(fù)雜度為：

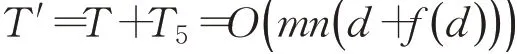
由此可知，與基本粒子群算法相比，LISPSO算法沒有增加額外的時(shí)間復(fù)雜度，執(zhí)行效率并沒有下降。

4 數(shù)值實(shí)驗(yàn)與結(jié)果分析

4.1 測(cè)試函數(shù)

為了測(cè)試算法的有效性，本文從2017年的基準(zhǔn)函數(shù)測(cè)試集中選取了11個(gè)基準(zhǔn)測(cè)試函數(shù)：

（1）Sphere函數(shù)

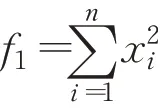
（2）Schwefel函數(shù)

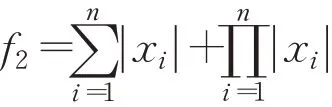
（3）Sum of Different Powers函數(shù)

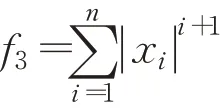
（4）Alpine函數(shù)

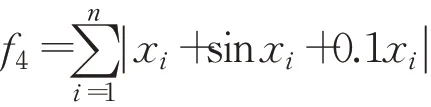
（5）Sum Squares函數(shù)

（6）Rastrigin函數(shù)

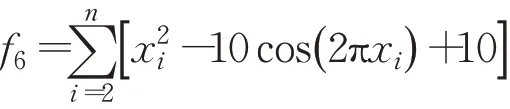
（7）powell函數(shù)

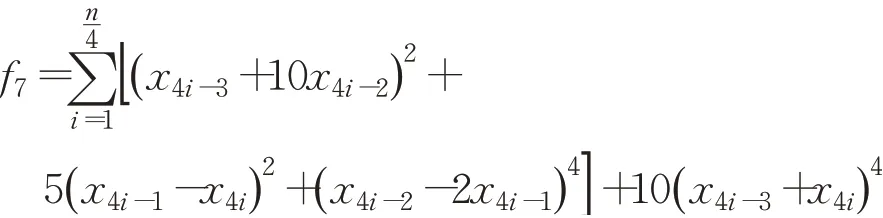
（8）Griewank函數(shù)

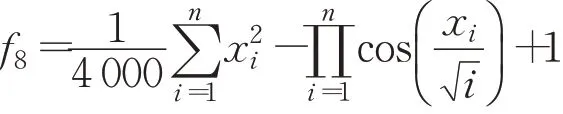
（9）Zakharov函數(shù)

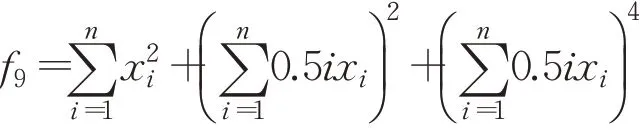
（10）Needle-in-a-haystack函數(shù)

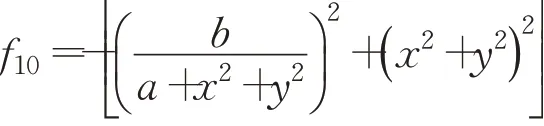
（11）Michalewicz’s函數(shù)

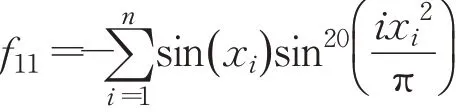
其中，f1～f9的理論最優(yōu)值為0，f10的理論最優(yōu)值近似為-3 600,f11的理論最優(yōu)值為：

4.2 與其他算法實(shí)驗(yàn)對(duì)比

4.2.1 數(shù)值實(shí)驗(yàn)

為了測(cè)試改進(jìn)粒子群算法LISPSO的性能，將本文算法LISPSO與SPSO、HCPSO算法進(jìn)行數(shù)值實(shí)驗(yàn)對(duì)比，其中，SPSO是簡(jiǎn)化粒子群算法[5]，HCPSO是文獻(xiàn)[13]提出的基于分層自主學(xué)習(xí)的改進(jìn)粒子群優(yōu)化算法（Particle Swarm Optimization based on Hierar Chical autonomous learning）。LISPSO與SPSO算法的種群大小設(shè)置為40，慣性權(quán)重w設(shè)置為0.6，學(xué)習(xí)因子c1、c2均設(shè)置為2.05，wmax、wmin分別設(shè)置為0.9和0.5。HCPSO算法的參數(shù)按照文獻(xiàn)[12]進(jìn)行設(shè)置。三種算法的迭代次數(shù)均設(shè)置為500。

為了測(cè)試本文算法對(duì)不同維函數(shù)的求解能力，f1～f9維數(shù)設(shè)置為10維、50維，f10維數(shù)設(shè)置為2維，f11維數(shù)設(shè)置為2維、5維。每個(gè)算例用這三種算法獨(dú)立運(yùn)行20次，并計(jì)算這20次的平均值及最優(yōu)值，將其作為最終的實(shí)驗(yàn)結(jié)果，得到表1、表2。另外，為了能更直觀地比較出實(shí)驗(yàn)結(jié)果的好壞，在編寫函數(shù)時(shí)，將函數(shù)f10、f11的理論非零值轉(zhuǎn)化為零，實(shí)驗(yàn)結(jié)果越接近零，則說明數(shù)值效果越好。將f1～f9維數(shù)設(shè)置為50維，f10維數(shù)設(shè)置為2維，f11維數(shù)設(shè)置為5維。畫出三種算法在11種基準(zhǔn)測(cè)試函數(shù)下的收斂曲線圖，見圖1。其中，表1、表2中加粗部分為實(shí)驗(yàn)對(duì)比的最好結(jié)果。

4.2.2 實(shí)驗(yàn)結(jié)果分析

由表1、表2可以看出，對(duì)于上述11個(gè)基準(zhǔn)測(cè)試函數(shù)，HCPSO算法表現(xiàn)出來的尋優(yōu)性能隨著維數(shù)的增加逐漸下降。SPSO算法受維度的影響不是很大，但除了f6、f8和f10函數(shù)，SPSO在求解其他函數(shù)時(shí)均未達(dá)到理論最優(yōu)值。而對(duì)于函數(shù)f1～f10，LISPSO算法在不同維數(shù)下找到的最優(yōu)解以及平均值均為理論最優(yōu)值。其尋優(yōu)性能遠(yuǎn)超于SPSO算法和HCPSO算法。雖然三種算法對(duì)理論最優(yōu)值與維數(shù)相關(guān)的函數(shù)f11求解結(jié)果均未達(dá)到理論最優(yōu)值，但無論是2維還是5維，LISPSO的求解性能均優(yōu)于其他兩種對(duì)比算法。

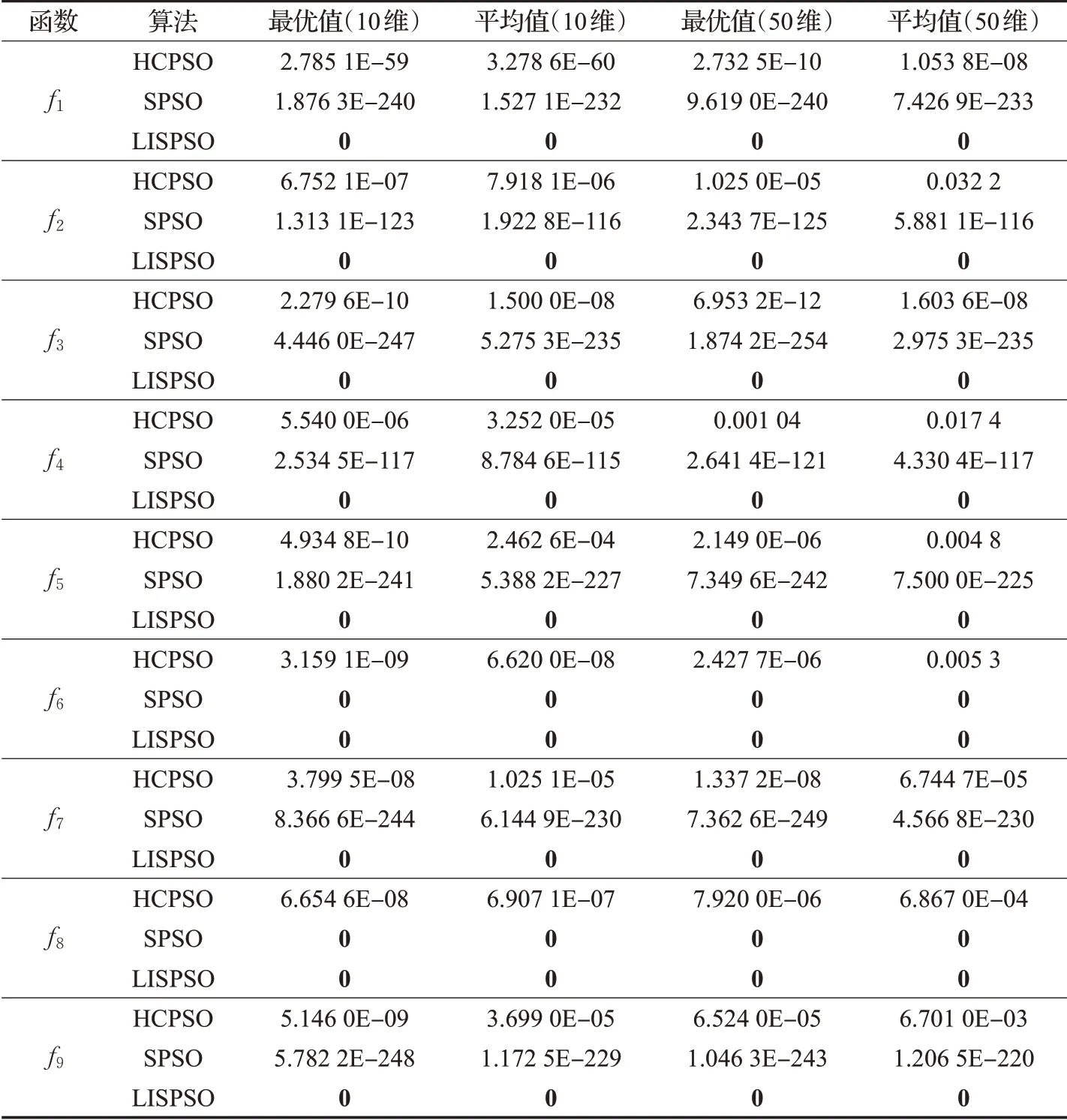
表1 三種算法對(duì)f1～f9的測(cè)試結(jié)果對(duì)比Table 1 Comparison of test results of three algorithms for f1～f9

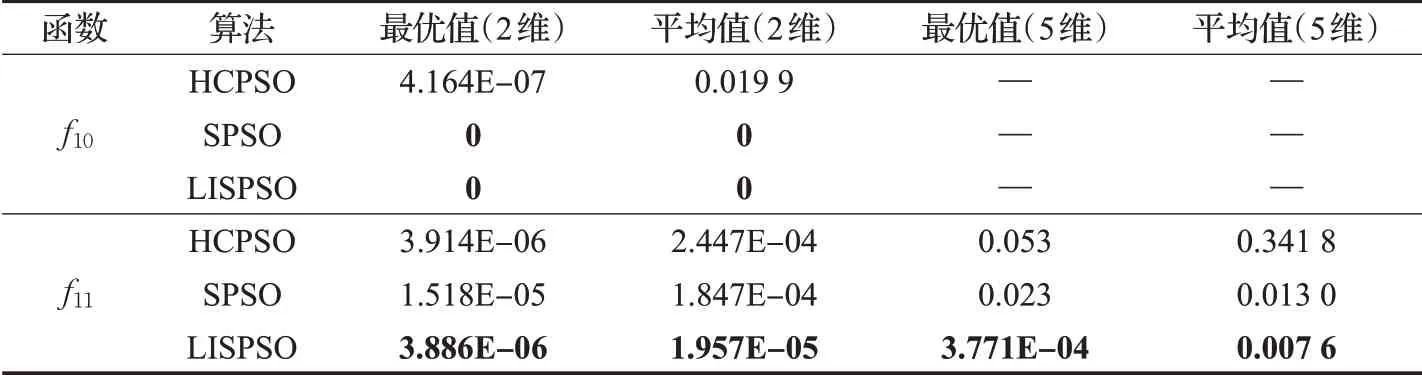
表2 三種算法對(duì)f10～f11的測(cè)試結(jié)果對(duì)比Table 2 Comparison of test results of three algorithms for f10～f11

另外圖1（a）～（k）清晰地展現(xiàn)了在迭代次數(shù)為500、函數(shù)維數(shù)為2維、5維或者50維的情況下，各種算法收斂曲線的變化趨勢(shì)。觀察圖1（a）～（j），對(duì)于每一個(gè)算例，LISPSO算法的收斂速度均優(yōu)于其他兩種對(duì)比算法，且均能在150代以內(nèi)收斂成功，達(dá)到理論最優(yōu)值。HCPSO表現(xiàn)的尋優(yōu)性能相對(duì)較差。雖然對(duì)于函數(shù)f6、f8和f10，SPSO與LISPSO均達(dá)到理論最優(yōu)值，但從收斂圖上看，LISPSO的收斂速度還是優(yōu)于SPSO。無論是收斂速度還是求解精度，本文算法LISPSO均優(yōu)于其他兩種對(duì)比算法。

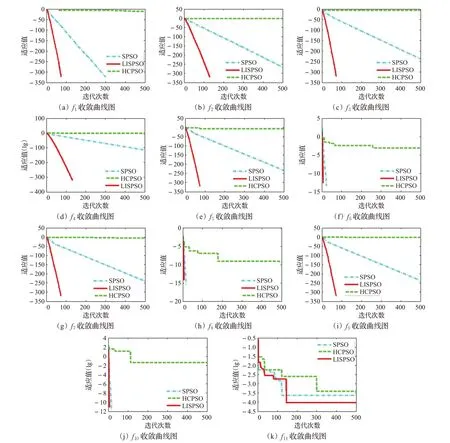
圖1 三種算法的適應(yīng)值迭代趨勢(shì)圖Fig.1 Iterative trend maps of fitness values of three algorithms

4.3 慣性權(quán)重的有效性分析

本文在位置更新公式中引入了帶有隨機(jī)性的非線性遞減慣性權(quán)重，不僅可以協(xié)調(diào)局部和全局的搜索能力，添加的rand隨機(jī)數(shù)更是保持了w的多樣性。為了進(jìn)一步說明改進(jìn)慣性權(quán)重的有效性，將LISPSO與LISPSOW、LISPSOC進(jìn)行數(shù)值實(shí)驗(yàn)對(duì)比。其中，LISPSOW是把LISPSO算法中的慣性權(quán)重w換成標(biāo)準(zhǔn)粒子群算法（文獻(xiàn)[2]）中的線性遞減慣性權(quán)重。LISPSOC是把LISPSO算法中的慣性權(quán)重w換成文獻(xiàn)[7]中的常數(shù)因子(w=0.6)。函數(shù)維數(shù)選擇50維、5維或者2維，每個(gè)函數(shù)用這三種算法獨(dú)立運(yùn)行20次，其他參數(shù)同4.2節(jié)。表3為數(shù)值實(shí)驗(yàn)結(jié)果，圖2為三種算法的尋優(yōu)收斂曲線圖，這里只選擇了f3、f5、f6、f7和f10五種函數(shù)的收斂曲線圖。

觀察表3、表4，LISPSO在求解f1～f10時(shí)均達(dá)到了理論最優(yōu)值。雖然LISPSO在求解f11時(shí)，并未達(dá)到理論最優(yōu)，但從數(shù)值結(jié)果來看，LISPSO的求解精度優(yōu)于其他兩種對(duì)比算法。另外兩種對(duì)比算法在求解除f6、f8和f10之外的函數(shù)時(shí)均未達(dá)到理論最優(yōu)解。三種算法中，LISPSO不僅在求解精度上表現(xiàn)最佳，從圖2也可以看出，LISPSO在收斂速度方面也明顯快于其他兩種對(duì)比算法。數(shù)值結(jié)果均表明，改進(jìn)的慣性權(quán)重優(yōu)于文獻(xiàn)[2]中非線性遞減的慣性權(quán)重和文獻(xiàn)[7]中的常數(shù)慣性權(quán)重，達(dá)到較好的協(xié)調(diào)局部和全局搜索的效果。

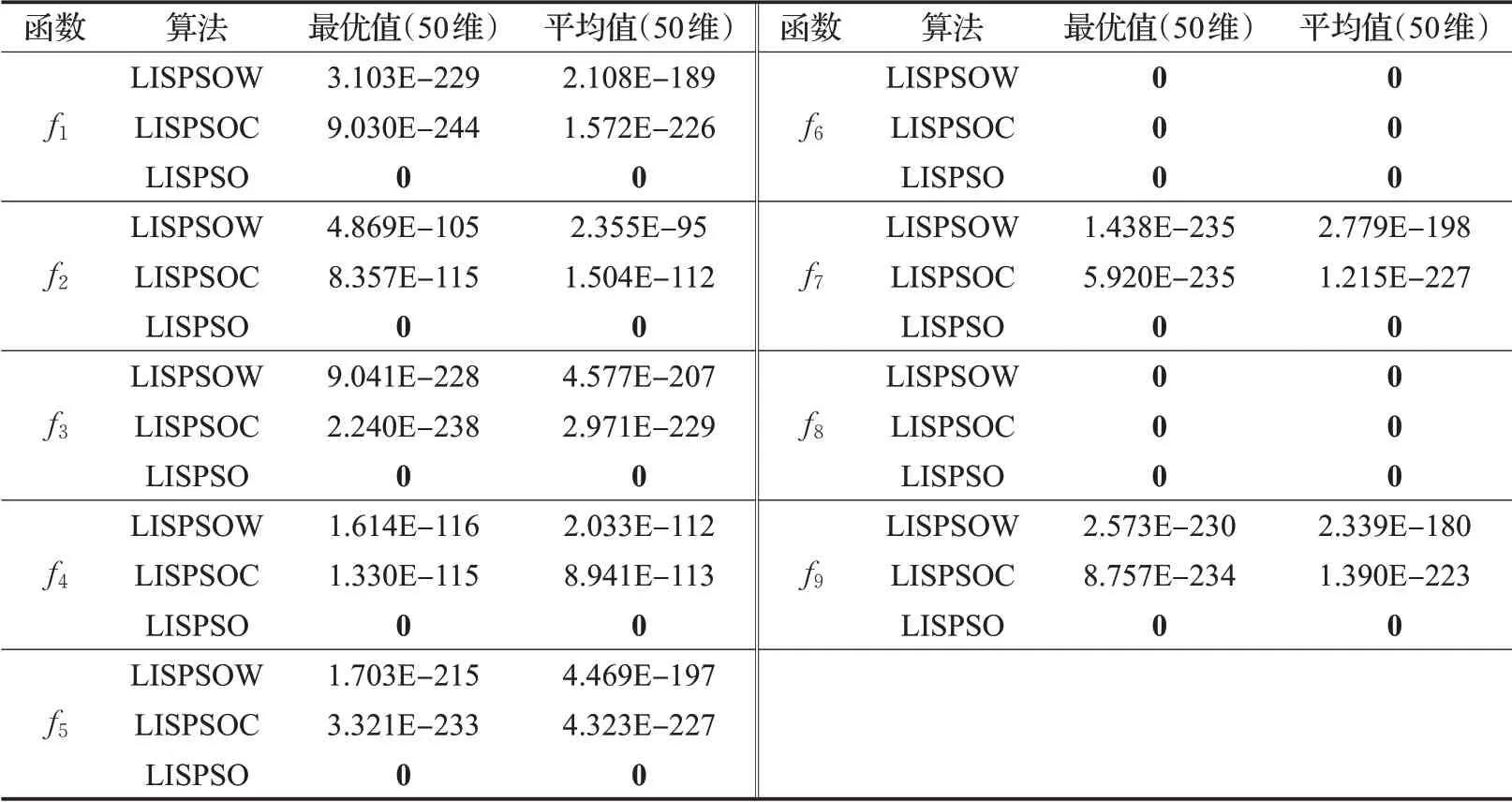
表3 不同慣性權(quán)重算法對(duì)比結(jié)果(f1～f9)Table 3 Comparison results of different inertia weight algorithms(f1～f9)

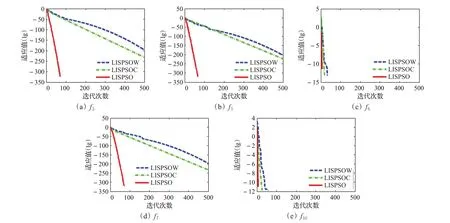
圖2 LISPSO、LISPSOW和LISPSOC算法收斂圖Fig.2 Convergence graphs of LISPSO，LISPSOW and LISPSOC

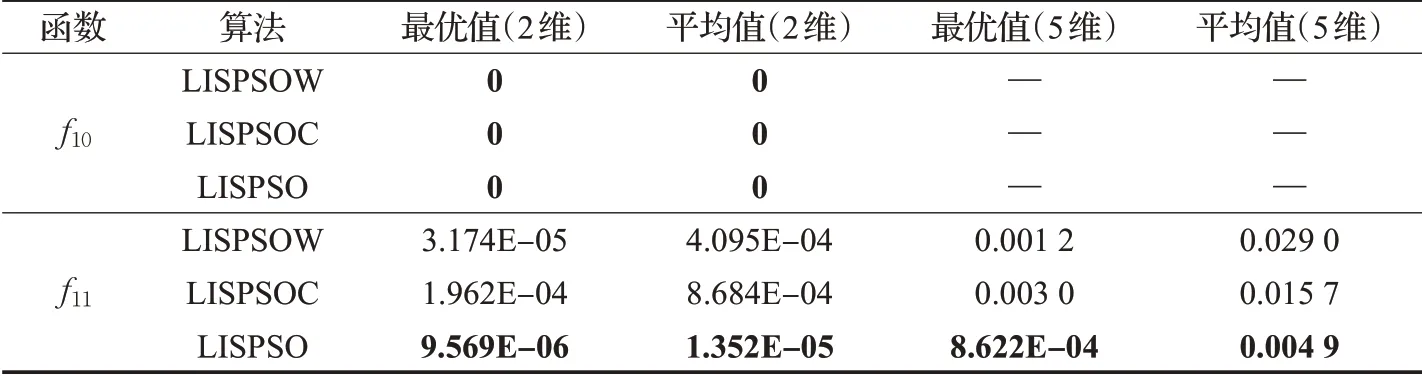
表4 不同慣性權(quán)重算法對(duì)比結(jié)果(f10～f11)Table 4 Comparison results of different inertia weight algorithms(f10～f11)

5 LISPSO算法求解min-max-min問題

5.1 min-max-min問題

min-max-min問題是一類不可導(dǎo)優(yōu)化問題，其表達(dá)式如下：

min-max-min問題在電子線路設(shè)計(jì)、工程優(yōu)化設(shè)計(jì)、控制系統(tǒng)優(yōu)化設(shè)計(jì)等方面應(yīng)用廣泛。它是典型的不可微問題，所以無論是從理論上還是計(jì)算上，解決起來均比較困難。不過仍有一些學(xué)者利用智能算法或者區(qū)間算法解決min-max-min問題：文獻(xiàn)[14]將提出的混合三群粒子群算法應(yīng)用到min-max-min問題，并取得較好的數(shù)值效果；文獻(xiàn)[15-16]利用區(qū)間算法對(duì)無約束的minmax-min問題進(jìn)行求解。本文利用LISPSO算法求解一類min-max-min問題，并進(jìn)行數(shù)值實(shí)驗(yàn)。令：

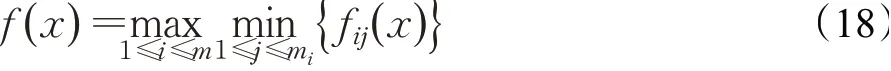
那么問題（17）轉(zhuǎn)化為：

min-max-min的適應(yīng)度函數(shù)定為式（18），和前面基準(zhǔn)測(cè)試函數(shù)一樣，求解函數(shù)（18）的極小值。將三種算法HCPSO、SPSO和LISPSO應(yīng)用到以下兩個(gè)min-max-min問題，比較它們的算法性能。其中，x*、f*、X(0)分別表示精確最優(yōu)點(diǎn)、精確值和初始搜索區(qū)間。

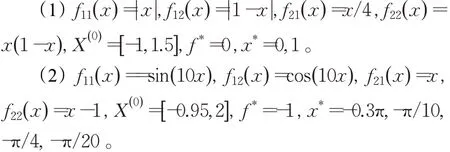
HCPSO、SPSO以及LISPSO的參數(shù)同4.2節(jié)，每個(gè)算例運(yùn)行20次，最大迭代次數(shù)設(shè)置為100，計(jì)算這20次的最優(yōu)值、平均值和方差，見表5，最好的結(jié)果用粗體表示。三種算法的收斂曲線圖見圖3、圖4。

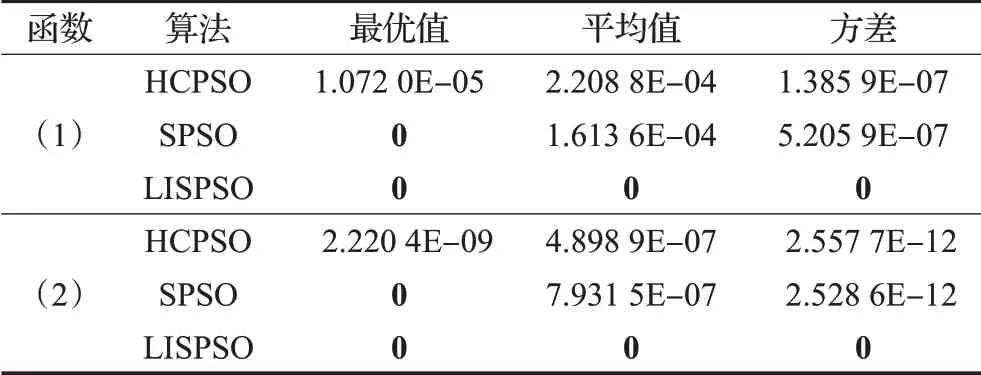
表5 兩個(gè)min-max-min問題的運(yùn)行結(jié)果Table 5 Results of two min-max-min problems

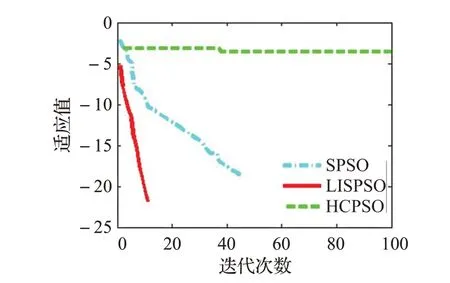
圖3 問題（1）收斂圖Fig.3 Convergence graph of problem（1）

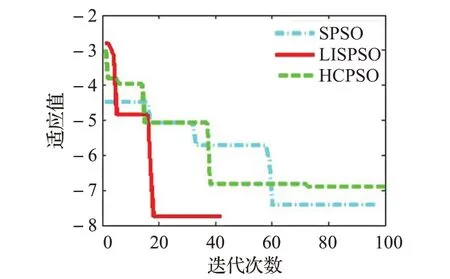
圖4 問題（2）收斂圖Fig4 Convergence graph of problem（2）

5.2 min-max-min問題的數(shù)值實(shí)驗(yàn)結(jié)果分析

觀察表5，對(duì)于兩個(gè)min-max-min函數(shù)，本文算法LISPSO均可達(dá)到理論最優(yōu)值，表現(xiàn)出較好的尋優(yōu)性能。雖然SPSO算法也可以達(dá)到理論最優(yōu)值，但從平均值和方差來看，SPSO算法求解非常不穩(wěn)定。相對(duì)于LISPSO和SPSO，HCPSO求解精度較差。從圖3和圖4來看，LISPSO的收斂速度也明顯快于其他兩種對(duì)比算法。

以上算例均表明，改進(jìn)的算法求解min-max-min問題是行之有效的，且無論是求解精度還是收斂速度，本文算法都表現(xiàn)出較好的尋優(yōu)性能。

6 結(jié)束語

為了避免粒子陷入局部最優(yōu)，提出了一種基于萊維飛行的改進(jìn)簡(jiǎn)化粒子群算法（LISPSO）。首先該算法舍去速度項(xiàng)，僅由粒子的位置控制粒子的進(jìn)化方向。其次，LISPSO算法在每次迭代都隨機(jī)地、非線性遞減地更新慣性權(quán)重，較好地協(xié)調(diào)全局和局部搜索。最后，算法融入基于相似度及聚集度分析的萊維飛行，幫助粒子跳出局部最優(yōu)。數(shù)值實(shí)驗(yàn)結(jié)果更直觀地表明LISPSO算法能夠增強(qiáng)粒子跳出局部最優(yōu)的能力，提高算法尋優(yōu)精度及收斂速度。

另外，將LISPSO算法應(yīng)用于求解一類min-maxmin問題，取得了較好的數(shù)值效果，體現(xiàn)出LISPSO算法解決一類min-max-min問題的可靠性和有效性。