Spinor F =1 Bose–Einstein condensates loaded in two types of radially-periodic potentials with spin–orbit coupling?
Ji-Guo Wang(王繼國) Yue-Qing Li(李月晴) Han-Zhao Tang(唐翰昭) and Ya-Fei Song(宋亞飛)
1Department of Mathematics and Physics,Shijiazhuang TieDao University,Shijiazhuang 050043,China
2Institute of Applied Physics,Shijiazhuang TieDao University,Shijiazhuang 050043,China
Keywords: spinor Bose–Einstein condensates,spin–orbit coupling,radially-periodic potential
1. Introduction
Spinor Bose–Einstein condensates (BECs) had been experimental realized in Na23and Rb87using dipole optical trap by the Tin-Lun Ho and Tetsuo Ohmi groups in 1998.[1,2]Three spin degrees of freedom are shown in spinor BECs,which corresponding to the three hyperfine spin states withmF=?1,0, 1 forF=1. Within the mean-field theory, spinorF=1 BECs show a rich variety of magnetic phenomena. The ferromagnetic state,antiferromagnetic state or polar state are exhibited in spin-1 BECs, the types of the ground-state phases are depended on the spin-exchange interaction. Many interesting topological excitations of the spin vortex, monopoles,two-dimensional (2D) skyrmion and three-dimensional (3D)skyrmion are proposed from these phases.[3–11]In addition,different types of solitons have been given rise to much attention in spin-1 BECs, such as the dark soliton, bright soliton, bright-dark soliton complexes, gap soliton and rogue wave.[12–20]
The realization of spin–orbit coupling (SOC) in spinor gases in experiment[21]opens fascinating questions about the physics of spin–orbit coupled ultracold gases, it has aroused the theoretical and experimental attentions on spin–orbit coupled BECs rapidly.[22–31]Two distinct phases,i.e., single plane-wave state and density-stripe state are found in a homogeneous spin–orbit coupled spin-1/2 BECs[32]and the quantum states with Skyrmion lattice patterns are emerged[25]in spin–orbit coupled spin-1/2 BECs loaded in a harmonic trap.Three kinds of striped phases with qualitatively different behaviors in the modulations of the density profiles in a homogeneous spin–orbit coupled spin-1 BECs depended on the antiferromagnetic interaction or ferromagnetic interaction.[33–36]Recently,spin–orbit coupled spinor BECs in the different periodic potentials, like the toroidal trap, spin-dependent periodic potential and radially-periodic potential are investigated, which results in many exotic ground-state phases and solitons.[37–46]
In this paper, we consider 2D spin–orbit coupled spin-1 BECs in two types of radially-periodic potentials,i.e., spinindependent and spin-dependent radially-periodic potentials.For the BECs in a spin-independent radially-periodic potential,the density of each component exhibits the periodic density modulation along the azimuthal direction, which realizes the necklacelike state in the ferromagnetic BECs. As the spinexchange interaction increases, the necklacelike state gradually transition to the plane wave phase for the antiferromagnetic BECs with larger SOC. The competition of the spindependent radially-periodic potential,SOC and spin-exchange interaction gives rise to the exotic ground-state phases when the BECs in a spin-dependent radially-periodic potential.
The paper is organized as follows. In Section 2 we introduce the model of 2D spin–orbit coupled spin-1 BECs in a radially periodic potential.In Section 3 we display the groundstate phases of spin–orbit coupled spin-1 BECs in a spinindependent radially periodic potential in Subsection 3.1 and pin-dependent radially periodic potential in Subsection 3.2. A brief summary is included in Section 4.
2. Model and Hamiltonian
We consider spin–orbit coupled spin-1 BECs loaded in the radially-periodic potential. The Hamiltonian can be described by the mean-field approximation,it is

whereωis the harmonic trap frequency, andV1(r) is the radially-periodic potential. Here, spin–orbit coupled spin-1 BECs loaded in two types of radially-periodic potentials are discussed,i.e., spin-independent or spin-dependent radiallyperiodic potential. The spin-independent radially-periodic potential isV1(r)=V0cos2(πr). The spin-dependent radiallyperiodic potential isV1(r)=V0cos2(πr+δ),whereδ=0 for themF=0 component andδ=π/2 for themF=±1 components.
3. Spin–orbit coupled spin-1 BECs in the radially-periodic potentials
We discuss the ground-state phases of spin–orbit coupled spin-1 BECs loaded in spin-independent and spin-dependent radially-periodic potentials in Subsection 3.1 and Subsection 3.2, respectively. Three dimensionless coupled timedependent Gross–Pitaevskii (GP) equations are formulated that from iˉh(?Ψj/?t)=δE/δΨ?j,

We obtain the ground-state phases by using the timesplitting Fourier pseudospectral method with the imaginarytime propagation,i.e.,t →?it.[47,48]The wave function in Eq. (4) can be written asΨj(r,t)=∑k=1Ψjk(r)exp(?itEk)with the eigenvalueEk. After each iteration, each eigenfunction is decayed by exp(?itEk), the returned wave function eigenvalue becomes lower and lower, it tends to the ground-state wave function, which lead to the proportion of the ground-state wave functions becomes larger and larger.When the time is at its limit,the wave functions evolve into the ground-state wave functions. The density–density interaction(c0=1000)and the radially-periodic potential depth(V0=20)are fixed.
3.1. Spin-independent radially-periodic potential
We first study on the ground-state phases of spin–orbit coupled spin-1 BECs loaded in a spin-independent radiallyperiodic potential. For the ferromagnetic BECs with spinexchange interactionc2=?200,the ground-state density profiles are shown in Fig. 1. The SOC strengths in panels (a)–(d) areγ=0, 1, 3, and 5, respectively. The columns from left to right are the densities of themF=?1 component, themF=0 component,themF=1 component,the total component,the density difference of themF=1 component,and themF=?1 component, the phase of themF=?1 component and the phase ofmF= 0 component. The density of each component is uniform distributed in the same ring without SOC,as shown in Fig.1(a). By considering SOC,we can find that the density of each component exhibits the periodic density modulation along the azimuthal direction. For the small SOC strengthγ= 1, the densities of themF=?1 and themF=1 components mainly occupy right and left sides, they are symmetric about theyaxis,one can be seen in Figs.1(b1)and 1(b3),respectively. The density difference of themF=1 component and themF=?1 component in Fig. 1(b4) also shows this character. In Fig. 1(b2), themF=0 component density shows a necklacelike state,the numbers of petals double increase as the ring expands one ring outward. With the SOC strength enhances,the phenomena of the periodic density modulation in each component become more obvious. The phases of themF=?1 and themF=1 components exhibit the rotational symmetry withγ=3 in Figs.1(c6)and 1(c7),however, they show the alternating plane waves that propagating on opposite directions along theyaxis for larger SOC strength in Figs.1(d6)and 1(d7),which are similar to the character of the supersolid state.[41,42]
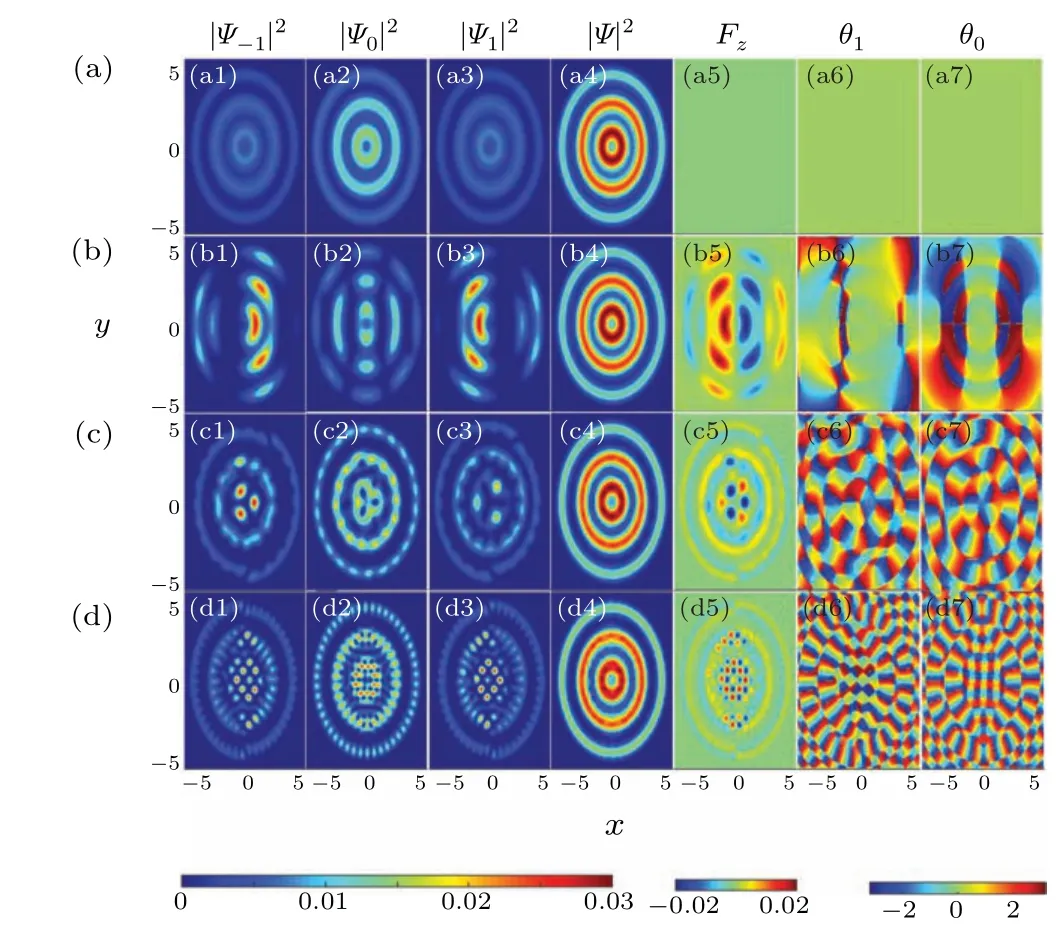
Fig. 1. The ground-state density profiles of spin-1 BECs with SOC loaded in a spin-independent radially periodic potential. The SOC strengths in panels (a)–(d) are γ =0, 1, 3, and 5, respectively. The columns from left to right are the densities of the mF =?1 component, the mF =0 component,the mF =1 component, the total component, the density difference of the mF =1 component,and the mF =?1 component,the phase of the mF =?1 component and the phase of the mF =0 component. The spin-exchange interaction c2=?200.


Fig. 2. The ground-state density profiles of spin-1 BECs with SOC loaded in a spin-independent radially periodic potential. The SOC strengths in panels (a)–(d) are γ =0, 1, 3, and 5, respectively. The columns from left to right are the densities of the mF =?1 component, the mF =0 component,the mF =1 component,the total component,and the phase of the mF =?1 component. The spin-exchange interaction c2=200.
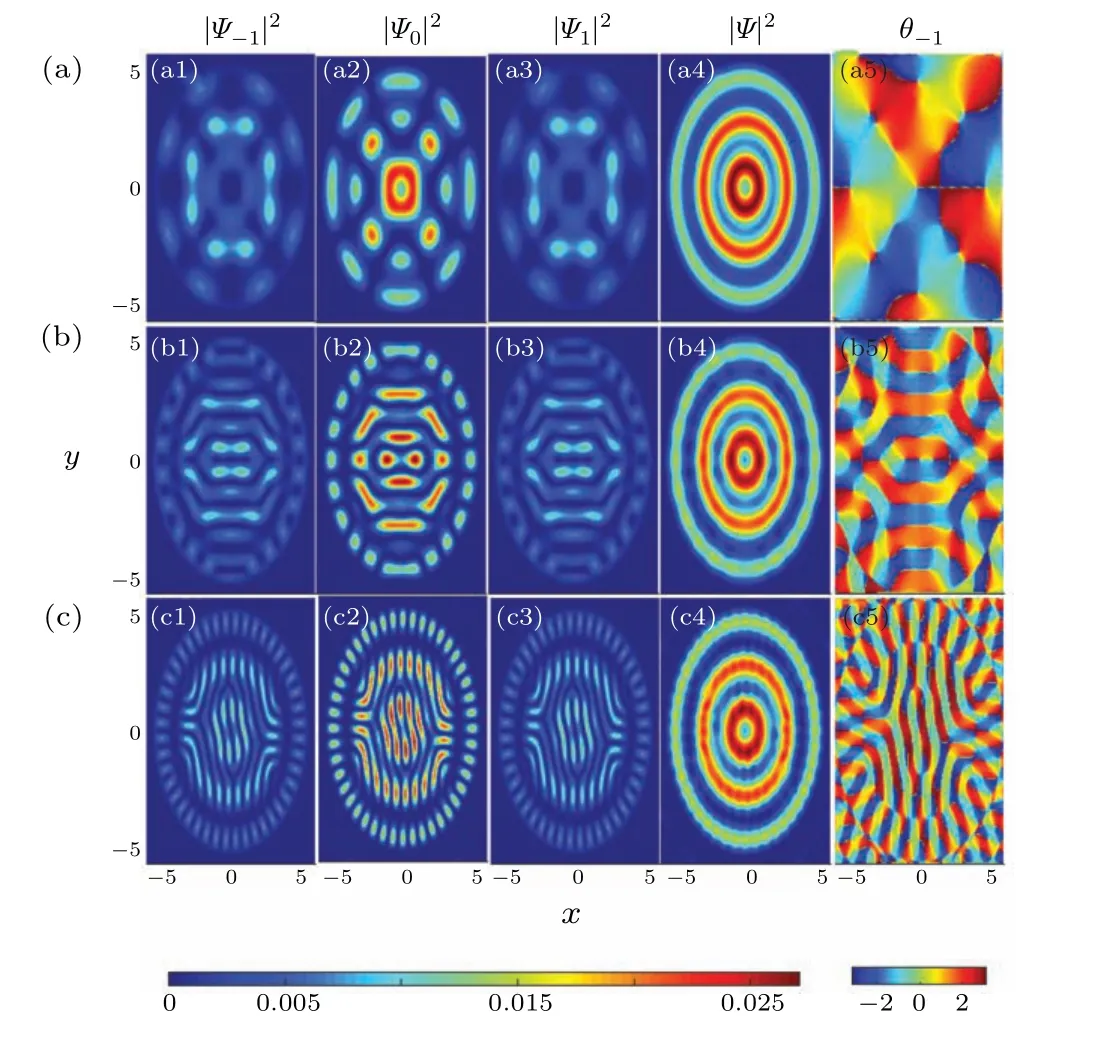
Fig. 3. The ground-state density profiles of spin-1 BECs with SOC loaded in a spin-independent radially periodic potential. The SOC strengths in panels(a)–(c)are γ=1,3,and 5,respectively.The columns from left to right are the densities of the mF =?1 component,the mF =0 component,the mF =1 component,the total component,and the phase of the mF =?1 component.The spin-exchange interaction c2=2000.


3.2. Spin-dependent radially-periodic potential
We next consider spin–orbit coupled spin-1 BECs loaded in a spin-dependent radially-periodic potential. The groundstate density profiles are shown in Fig. 4 with the different spin-exchange interactions strengthsc2=?200, 200, and 2000 in panels(a)–(c),respectively. The SOC strengthγ=5.The competition of the spin-dependent radially-periodic potential, SOC and spin-exchange interaction gives rise to the exotic ground-state phases. For the ferromagnetic BECs, the spin-dependent radially-periodic potential and SOC break the translational symmetry of density along one direction,and the translational symmetry along the direction that perpendicular to it is preserved. For the antiferromagnetic BECs, the density of each component shows the ring structure with spinexchange interactionc2= 200 in Fig. 4(b). The innermost rings consist of two semicircles in themF=±1 components,which results in the density of themF=0 component is divided into two half arcs. The structure of innermost rings of the total density is similar to the double lung of human organs.An interesting phenomenon in Fig.4(b5),the phase profile of themF=?1 component consists of alternating vortices along the opposite directions,which is caused by the spin-dependent radially-periodic potential and SOC.As the spin-exchange interaction increases,the ring structures are broken. The double vortices are shown in the phase profile of themF=?1 component in Fig.4(c).

Fig.4. The ground-state density profiles of spin-1 BECs with SOC loaded in a spin-dependent radially periodic potential. The spin-exchange interactions in panels (a)–(c) are c2 =?200, 200, and 2000, respectively. The columns from left to right are the densities of the mF =?1 component, the mF =0 component, the mF =1 component, the total component, and the phase of the mF =?1 component. The SOC strength γ =5.
4. Summary
In summary,we have investigated 2D spin–orbit coupled spin-1 BECs in two types of radially-periodic potentials,i.e.,spin-independent and spin-dependent radially-periodic potentials. For the BECs in a spin-independent radially-periodic potential,the density of each component exhibits the periodic density modulation along the azimuthal direction realizes the necklacelike state in the ferromagnetic BECs. As the spinexchange interaction increases, the necklacelike state gradually transition to the plane wave phase for the antiferromagnetic BECs with larger SOC. The competition of the spindependent radially-periodic potential,SOC and spin-exchange interaction gives rise to the exotic ground-state phases when the BECs in a spin-dependent radially-periodic potential.
- Chinese Physics B的其它文章
- Physical properties of relativistic electron beam during long-range propagation in space plasma environment?
- Heterogeneous traffic flow modeling with drivers’timid and aggressive characteristics?
- Optimized monogamy and polygamy inequalities for multipartite qubit entanglement?
- CO2 emission control in new CM car-following model with feedback control of the optimal estimation of velocity difference under V2X environment?
- Non-peripherally octaalkyl-substituted nickel phthalocyanines used as non-dopant hole transport materials in perovskite solar cells?
- Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study?

