Electrostatic force of dust deposition originating from contact between particles and photovoltaic glass?

Xing-Cai Li(李興財) Juan Wang(王娟) and Guo-Qing Su(蘇國慶)

1School of Physics and Electronic-Electrical Engineering,Ningxia University,Yinchuan 750021,China

2Ningxia Key Laboratory of Intelligent Sensing&Desert Information,Ningxia University,Yinchuan 750021,China

3Xinhua College of Ningxia University,Yinchuan 750021,China

Keywords: particle electrification,electrostatic force,photovoltaic glass,dust deposition

1. Introduction

Dust particle deposition is an essential factor affecting the efficiency of the photovoltaic (PV) power generation system.[1,2]Studies have shown that a mass density of 0.4 mg/cm2of the dust on the PV panel can reduce the generation efficiency of the panel by about 30%, and even a small amount of deposited dust (0.06 mg/cm2) can lead the generation efficiency to decrease by about 2.5%.[3]According to some researches, the electrical efficiency of not-cleaned PV cells decreases from 16%to 8%over 45 days,but in Baghdad–Iraq, it dropped to less than 6.24% in one day, 11.8% in one week, and 18.74% in one month.[4–6]The influence of deposited dust particles on the power generation performance of PV panel is related to the mass and physical properties of the particles.[7]Long-term accumulation of dust particles will cause the hot spot effect of PV panel, and even damage the panel in severe cases.[8]An effective dust removing technology can wipe out the deposited dust and frequently using it can reduce the loss dramatically. The widespread existence of atmospheric aerosols is beneficial to the cleaning of the PV panel surface.[9]To clarify the deposition mechanism of dust on the PV panel surface may be helpful in designing a more cost-effective dust removing method or PV panel installation process.[9]

Numerical simulation research has been carried out on the sand & dust deposition on the surface of PV panel based on the fluid dynamics method in recent years. For example,Luet al. studied the flow field and the dust deposition process around the solar panel installed on the ground by adopting a technique coupling computational fluid dynamics(CFD)with the discrete particle model(DPM).[10]Another study discussed the deposition process and behavior of dust on groundmounted solar PV arrays based on the shear stress transportk-turbulence model and the discrete particle model.[11]Chitikaet al. investigated the parametric installation optimization for mitigating the non-tracking solar PV module fouling based on the CFD prediction of dust deposition.[12]Unfortunately, the above-mentioned studies only take the effects of the fluid force and gravity into account. However,the electric phenomenon caused by the contact between different materials has long been concerned.[13–17]The movement of particles in the air is bound to be accompanied by collisions with each other, which will lead to electrification and thus generate an electric field of a certain intensity in the air.[18,19]Few studies on the particle deposition considered the electrification in the atmosphere,except for the research of Cooperet al.,[20]who,however,explored the deposition of charged aerosol particles in the air rather than on the surface of PV panels.

There are also a lot of studies on the adhesion force between particles and plates. For example,Rimaiet al.[21]studied the mechanism of deformations induced by adhesion between micrometer-sized particles and various substrates, and then discussed the effective application ranges of several adhesion theories.In the analysis of the effect of various fundamental forces on the adhesion of fine dust particles,Walton[22]suggested the dominant role that van der Waals adhesion forces played in small-sized particles. In particular,they gave special regard to the electrostatic image force between a particle and a conductor plane.The study of Moutinhoet al.[23]revealed that the van der Waals forces and capillary forces play the leading role in attaching dust particles to PV modules. Jianget al.[24]used an atomic force microscope to measure the adhesion force between dust particles and PV modules under the action of an electrostatic field,and found that the electrostatic force is five times and one order of magnitude larger than the van der Waals force when applied voltage is 100 V and 100 V to 500 V, respectively. Another paper reported that the electrostatic force is 1 or 2 orders of magnitude stronger than the van der Waals force and the capillary hydraulic force,[25]indicating that the electrostatic force induced by the electric field generated by PV modules cannot be ignored. Obviously,such a kind of electrostatic force differs from that generated in the process of dynamic contact between the deposited particles and the PV glass.

According to the dynamic contact electrification mechanism, the PV glass will carry a great deal of static charges when contacted with a large number of moving particles,[26]and the resulting electrostatic field will increase the charges,[16,27]thus it also enhances the electrostatic force of moving particles.[28]Under certain conditions, more sand particles will be deposited on the PV panels.[29]However,the contact electrification between deposited dust and PV glass panels is rarely studied, and there is a lack of reports on the influence of such an electrostatic force on the dust deposition process. In view of these situations, in this work, the contact electrification between the deposited sand&dust and the PV panel is studied, and the electrostatic force of the electrified sand particles is analyzed. Furthermore,a new PV glass material is proposed based on the analysis.

2. Contact electrification model

The modeling of contact electrification mechanism is a classical problem,and a large number of physical models have been developed up to this time.[16,17,30–36]This paper adopts the physical model given by Xieet al.,[35]which can well describe the influence of the particle size ratio on its net charge.The basic equation of the model is

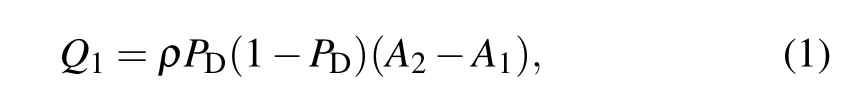
whereρis the surface charge density andPDis the probability of ion exchange,which is set to be 0.5.[35]The contact areaAi(i=1,2)of two colliding particles can be calculated from[35]

wherem1andm2are the masses of the two colliding particles, whose radii areR1andr1respectively,Eiandviare respectively the elastic modulus and Poisson’s ratio of the two particles,andvris the impact velocity.

The particle electrification mechanism model under the impact of an electrostatic field can be expressed as[38]

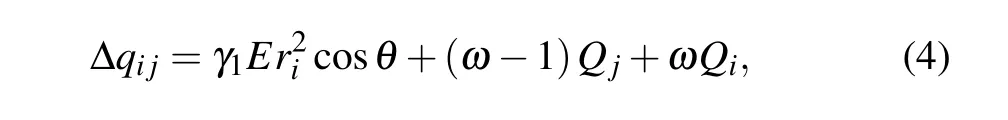
whereEis the environmental electric field,riis the radius of thei-th particle,θis the angle between the line of the particle center and the electric filed,QiandQjare the initial charge of thei-th andj-th particles,respectively,ωis the ratio between the charge of one particle transferred to other particles and this particle’s original charge,andγ1is the radius ratio of the two colliding particles.

Therefore, the charge of the particle after collision in an electric field is given as

In this paper,the collision occurs between the particle and the PV plate,so we assume that the radius of the massive particle is 1000 times larger than that of the smaller particle,similar to the treatment adopted in Ref.[19].

3. Electrostatic force acting on charged deposition particles

As shown in Figs.1 and 2,assuming the length of the PV panel to be 2aand the width to be 2b, a rectangular coordinate system is established by taking the center of the panel as the origin. The number concentration of particles in the atmosphere is represented byN, and the charge of particles is expressed by the charge–mass ratioqm. The coordinate of the center of the element is assumed to be (x,y,z) and the electric field intensity generated by it must have componentsEx,Ey, andEz. Owing to symmetry, there must be no horizontal electric field component and only a vertical component exists in the center of the plate. The three-dimensional(3D)electric field distribution can be found at other positions.

Fig.1. Scheme of electric field generated by airborne particles.

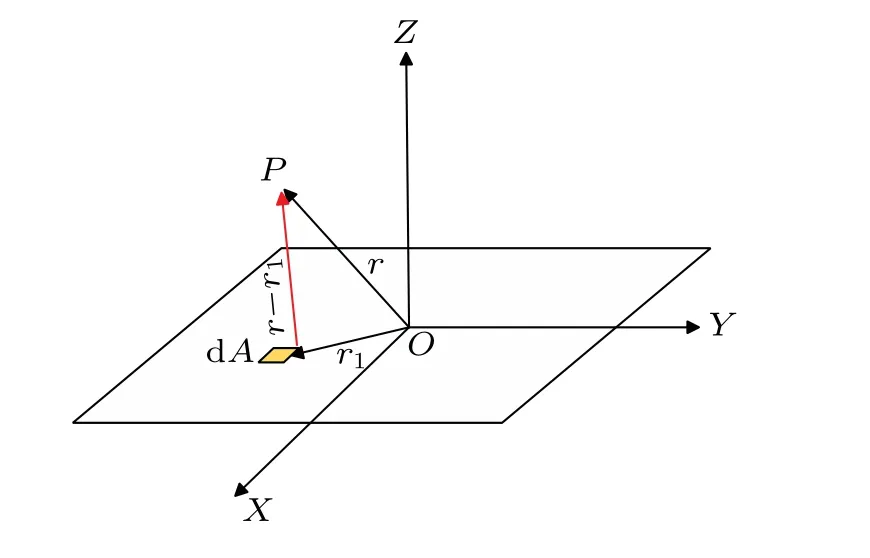
Fig.2. Scheme of electric field generated by plate.

Assuming the diameter of particles suspended in the air to beD,the particle mass density to beρ,the particle number concentration to beN(z),and the particle charge-mass ratio to beqm, the electric field at the position (x1,y1,z1) above the PV panel can be expressed as[39]

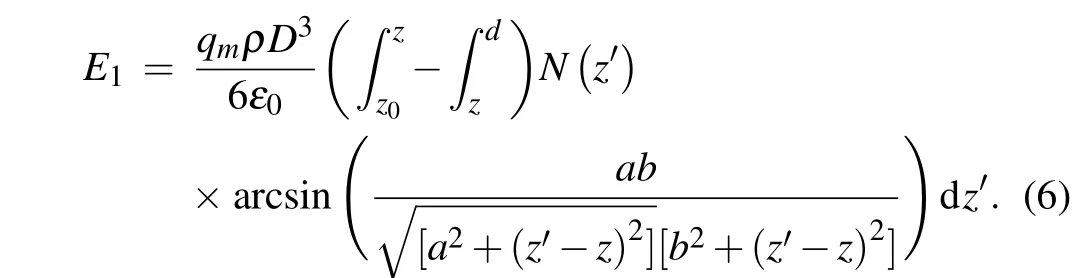
Considering the infinite nature of the space, the electric field generated by the sand particles suspended in the air has only a vertical component. Athough a single particle has a extremely small charge, the electrostatic field generated by the sand particles with a high concentration in the air should not be ignored. This extreme case is not considered in this paper.

When a large number of falling particles collide with or slide on the PV glass panel,both the particles and the PV panel carry some electrostatic charges, thus generating an electric field around the PV panel.[39–41]Smaller particles are negatively charged while the larger ones are positively charged,[42]so we assume that the charge-mass ratio of the deposition particle is?qm. According to the law of charge conservation,the PV glass plate carries the same number of charges as the number of deposition particles.If we assume the mass concentration of deposited particles in the atmosphere under specified conditions to bemq,the falling velocity to bev,and the horizontal projection area of the PV panel to beA, there is aboutmqvAtparticles colliding with the PV glass panel at timet.The relative movement between deposition particles and the PV panel charges the PV glass plate, whose surface charge density should be

When the distance between particles and the plate is a minimum value,the plate can be regarded as infinite,and then the electric field can be solvedE=σ/(2ε0).

Then,the electrostatic force applied to the charged particles can be calculated from

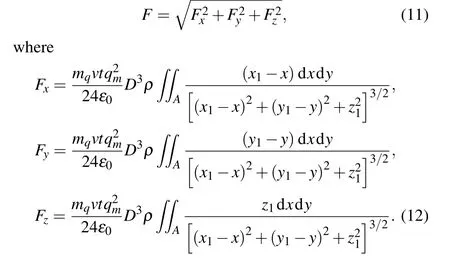
In order to highlight the effect of electrostatic force from the contact electrification process between the dust particles and the PV glass plate on the deposition and removal process of the particles, we compare the forces on the particles deposited on the tilted photovoltaic panels.

4. Results and analysis

Firstly,we measure the charge of polydisperse deposition particles when they fall from different heights and collide with tilted PV panels. We describe the particle charge by using the ratio of the charge to the mass of particle (i.e.charge–mass ratio)in this paper since it is widely used in the present research.[44]The schematic diagram of the experiment device and the particle size distribution function are shown in Fig.3.The dust particles used in the experiment are collected from the southeastern edge of the Tengger desert. When the particles fall free from a certain height, they will collide with and slide over the photovoltaic glass panel. Some of the particles remain on the glass panel, the other slides down the inclined plane and falls into the Faraday cup, from which we can obtain the total chargeQon the particles. Then we weigh the particles in the Faraday cup and record their massmsand. Now we can obtain the charge–mass ratioqm=Q/msand. In the experiment,the EST111 Static Charge Meter is used to measure the charge of the particles,the BSA224S electronic analytical balance is used to measure the mass of particles.

Fig. 3. (a) Schematic diagram of experimental construction and (b) size distribution of experimental particles.

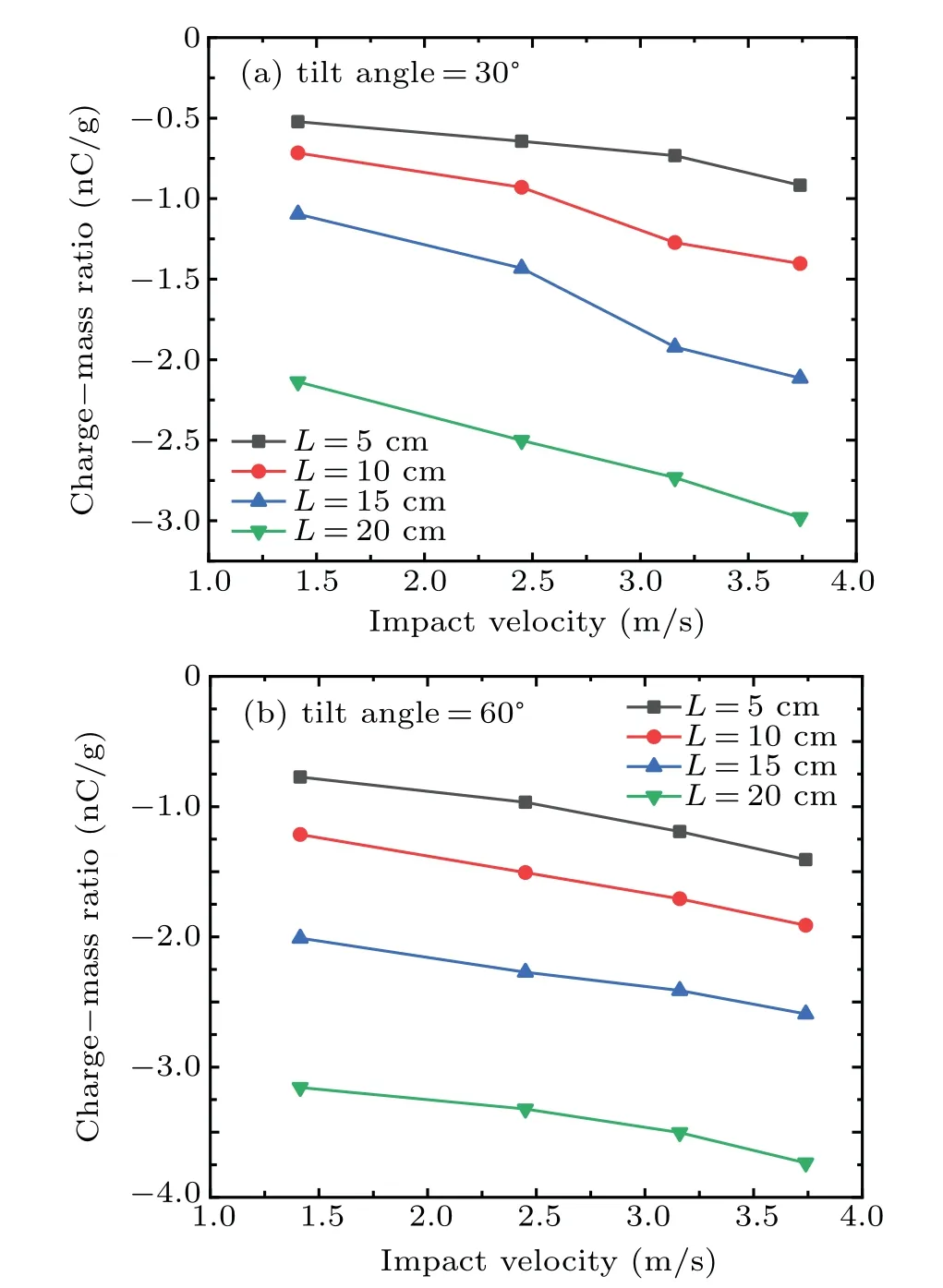
Fig. 4. Particle charge–mass ratios varying with impact velocity on an inclined PV glass panel at tilt angle(a)30° and(b)60° for different L values.

Figure 5 shows the variations of the charge–mass ratio of deposited dust particle with the sliding distance of particle on the PV glass plate. It is obvious that with the increase of the sliding distance and the drop height,the charge–mass ratio of particle increases nonlinearly. Besides,by comparing the four figures in Fig.5, it is easy to find that as the plate inclination angle increases,the charge–mass ratio of particle increases to different degrees. For this reason,the influence of the plate tilt angle on the particle charge–mass ratio is discussed in Fig.6,where the experiments on selected particles are conducted at a free-falling height of 30 cm and 70 cm,respectively. According to the figure,the charge–mass ratio of particle increases as the plate inclination angle enlarges, and a larger drop height results in a higher particle charge. As is well known,the particle’s charge increases more easily when it slides with a plate.The different experimental conditions make the motion states of particles and the contact mode between the particles and the glass plate changed. For example, when the plate inclination angle is small,the particles mainly roll,and with the increase of the angle, the sliding process of the particles is dominant,so the charge on particles increases.

Fig.5. Particle charge–mass ratios versus sliding distance on an inclined PV glass panel at tilt angle(a)30° and(b)60° for different h values.

Fig.6. Charge–mass ratios versus tilt angle on particle charge for different heights.

At the same time, we also measure the distribution of electrostatic field on the photovoltaic glass plate in the abovementioned experiment process. The result is shown in Fig.7.From it we can find that the electrostatic field shows a bellshaped distribution. This is determined by the cooperation of the electric field forces around the location.

In the above study, we involve with the charged rules of deposition particles after colliding with photovoltaic glass through some experimental measurements. Next, we will investigate the distribution law of electrostatic force received by particles through numerical simulation. These researches will be based on Eq. (11). The results are shown in Fig. 8.Here, we will set the particle distance to bez1=10 cm, the charge–mass ratio to be 2 nC/g, and the particle radius to be 35μm. The results show that the electrostatic forces are distributed in a bell shape,reaching a maximum value in the center of the plate and a minimum value around the edge of the plate. This law is consistent with the electric field distribution of PV glass plate obtained from the above-mentioned experiment. Although the electric quantity on the particle is small,the electrostatic force is still slightly higher than the gravity(4.66 nN),so it will change the deposition process of particles on the surface of photovoltaic panels. Therefore, it is necessary to consider the contact electrification process between deposited particles and the photovoltaic panels,especially the derived electrostatic force in the simulation of the dust deposition on the photovoltaic panels.

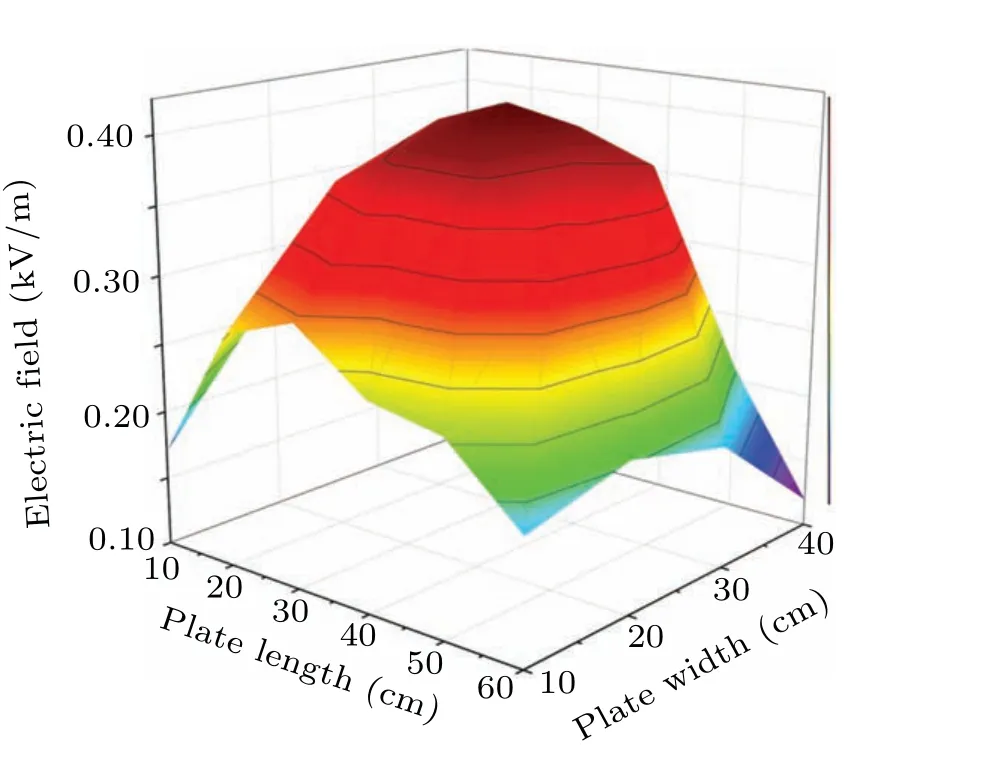
Fig.7. The E-field profile on charged PV plate.

Fig.8. Electrostatic force acting on charged particles.

As indicated in Fig.9,the rule of electrostatic force varies with the distance between charged particles and the PV glass plate is discussed. All the parameters are equal to those in Fig. 8, except for the distancez1between particles and the PV plate. We can see that the electrostatic forces fluctuate violently, which can be explained by the mutual attraction between two charged particles with the same charge and the tablet with the opposite charge, as reported in Ref. [7]. It should be pointed out that the numerical results also show that the electric field at the central position diverges with the decrease of the distance between the particles and the plate surface.

In order to analyze the magnitude relation among the electrostatic forces applied to particles of different sizes, we calculate the electrostatic force acting on particles with sizes of 15 μm, 25 μm, and 35 μm, located atz1=0.1 μm, and compare the results with those of particles each with a size of 5 μm. The simulation results shown in Fig. 10 indicate that the electrostatic force of particles increases significantly with the particle size increasing,which is attributed to the increasing of charge–mass ratio during the collision between particles and the plate surface. Besides, it can be seen from the figure that with the increase of the particle size,the electrostatic force applied to the particles does not always increase,but decreases tremendously in some regions.

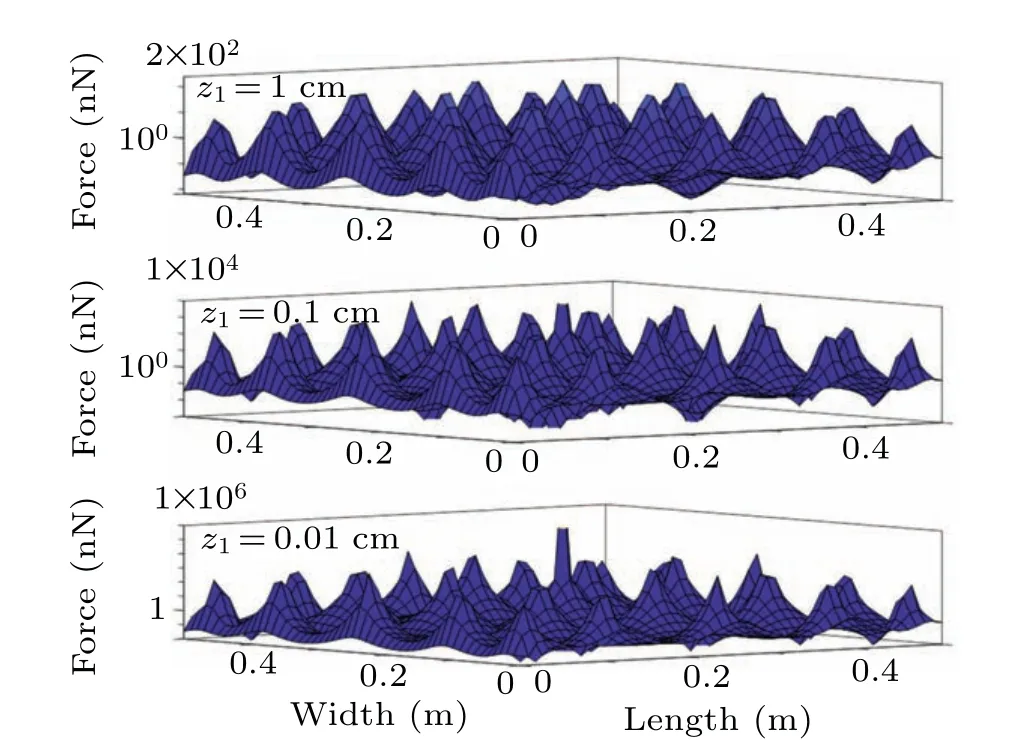
Fig.9. Distribution of electrostatic forces acting on charged particles at different places above PV panel.

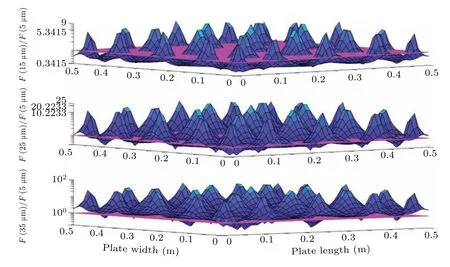
Fig.10. Electrostatic force ratios versus plate width and plate length of particles on flat surface.

Finally, we calculate the electrostatic force acting on the particle located atz1=1 nm and with a radius of 20μm and a charge of 2.464×10?16C from Eq.(11),and compare it with the results achieved by other studies. The results shown in Fig.11 reveal that the electrostatic force ranges from 10?4μN to 103μN, with an average value of 7 μN. This is basically consistent with the results of other literature. The electrostatic force is much higher than the gravity (0.87 nN) and the van der Waals force (1.8 nN),[25]indicating that the electrostatic force will promote more moving particles to deposit on the PV panel,thus resulting in a non-uniform distribution of dust particles deposited on the PV panel.

Fig.11. Distribution of electrostatic force versus width and length under the same parameters as in other studies.

5. Conclusions

We report the electrification phenomenon between deposition particles and PV panels, and analyze the charge–mass ratios of polydisperse dust particles that fall from different heights and collide with tilted PV glass panels. In addition,the corresponding physical model is established to discuss the electrostatic force of dust on the surface of electrified PV panels. The results show that the dust particles colliding with the PV glass plate will carry a large number of static charges,and the number of charges increases to different degrees with the increasing of the impact velocity and the inclination angle of the PV panel. Besides, a larger particle size and a higher impact velocity can significantly increase the electrostatic force exerted on particles,which is even higher than the gravity and the van der Waals force. In addition,the electrostatic force is relatively large in the plate center,and distributed in an oscillatory manner at different positions. On the whole, the electrostatic force caused by the collision of PV glass plates and deposited particles may enhance the deposition of moving particles on the surface of the PV panel and show a non-uniform distribution, which possibly has more complex implications for PV cells.[45,46]Therefore, an anti-static transparent material should be considered for the PV panel that serves in the severe wind-sand environment,for example,the solar powered devices of the Mars explorer. The results of this paper facilitate the understanding of the deposition mechanism of dust particles on the PV panels in dusty weather,and provide some theoretical support for the removing of dust particles deposited on the PV panel in the desert environment.