Analysis of natural frequency for imaging interface in liquid lens
Na Xie(謝娜)
College of Electronic and Optical Engineering and College of Microelectronics,Nanjing University of Posts and Telecommunications,Nanjing 210023,China
Keywords: natural frequency,liquid–liquid interface,capillary wave,liquid lens
1. Introduction
Since electrowetting liquid lens was innovated, it has been received increased attention across a number of scientific inquiries in recent years,[1–12]such as the imaging of portable lens,[4,5]realizing the bionic compound eyes,[6]composing array displays,[7]enhancement of scanning microscopes,[8,9]and construction of holographic display systems.[10]There were also interesting studies of the liquid–liquid (L–L) interface in the lens for interference imaging,[11]which can be used to enhance the encryption randomness of phase mask in optical communication systems to prevent confrontational attacks.[12]
In all kinds of applications,the rapid response of milliseconds is a major advantage for the liquid lens.[13]The response time mainly depends on the time difference between the applying of voltage signal and the stabilization of the L–L interface. Due to the instant electrical field establishment, the response time is mainly the interval between the changes of liquid–liquid–solid three-phase angle on the side wall to the stabilization of the L–L interface. In essence, the response characteristics of the surface wave on the interface is determined in a closed vessel,which is a capillary hydrodynamics problem as it is in capillary scale.
To date, previous studies have investigated the dynamic response of liquid lens based mainly on the experimental observations.[5,14–16]Some researchers used transparent cylinder wall for investigating the interface profiles,[5]and some employed the beam imaging to reflect the fluctuation characteristics of the lens indirectly.[15]Obviously,prior studies have not been able to convincingly show the theoretical basis of the liquid lens imaging interface fluctuation.[17]
In the last few decades,due to the aerospace and nuclear technology boom,there were extensive studies on the surface wave in vessels such as the fuel storage containers.[18–21]But as far as we know,there was no special study about the capillary wave on L–L interface in a closed container. In general,the electrowetting liquid lens is at the size around the capillary constant,which for water is 0.39 cm at 20°.The gravity can be neglected because the difference of the pressure due to gravity is zero at the L–L interface when the density of the liquids is as the same.
Recent developments in liquid lens have heightened the need for the theoretical basis of the lens. In this study, the hydrodynamic analysis of the L–L interface fluctuation based on the equations of Euler and fluid continuity is proposed,and the natural frequencies of capillary wave of modes 0 and 1 are obtained. The analytical results in our research are in a good consistent with the experiments documented in the literature. The influences of the radius, the height ratio and the height-to-diameter ratio of the double layer cylinder on natural frequencies are also studied. It is hoped that this research will contribute to a deeper understanding of the interface dynamics in the liquid lens and provide a basis for the precise control of the interface for beam modulation.
2. Research methods
2.1. Liquid lens model
With the same density,different viscosities and refractive indexes,the conductive ion water and insulating oil are encapsulated in a cylindrical container. The spherical L–L interface between the two liquids can modulate the beam spatially,and the diopter of the interface can be controlled by the applied voltage.
A simple model of the electrowetting liquid lens is shown in Fig. 1(a). The upper liquid is ion solution with heighth′,while the lower is oil with heighth,and both are encapsulated in a cylindrical container with radiusa. When no voltage applied, the three-phase angleαis obtuse at the internal wall where coated a thin hydrophobic layer,and it is a concave lens as the refractive index of the oil is larger. When the voltage is applied,according to Young’s equation,[3]the contact angleαbecomes smaller and the curvature of the interface changes accordingly,so the focal length changes.
In our previous studies,[22]it was found that the natural frequency of the interface decreases with the decrease of the interface curvature. Therefore,the natural frequency of the interface is affected apparently by the contact angle. To simplify the mathematical problem, here we focus on the fluctuation characteristics of a capillary wave on a flat interface, that is,the contact angle is equal to 90°, and the curvature of the interface is infinity. In this case, it is accurate to establish a mathematical model using cylindrical coordinates. Otherwise,the interface is spherical when the contact angle is not equal to 90°. The spherical coordinates are more suitable to solve the problem,but the theoretical analysis will be more complicated.

Fig. 1. (a)A liquid lens in a cylinder container with upper liquid ion water and lower oil. (b)The cylindrical coordinates of the lens.
2.2. Fluid dynamics equations
In accordance with the general assumptions of fluid dynamics, we assume that the upper water and lower oil are incompressible and irrotational fluids.[17]The fluctuation amplitude of the L–L interface is supposed to be small compared with the radius of the cylinder,so the linear surface wave approximation is established. The cylindrical coordinates are shown in Fig. 1(b), where the L–L interface is a plane and the origin is set on it. According to the hydrodynamics, the velocity potentialφof oil andφ′of water should satisfy the Laplace equations,respectively,which are By using the trigonometric function formula, the natural frequency can be written as


3. Results and discussion
3.1. Comparison with experiments
In order to compare with the experimental data of commercial lens Varioptic 39N0, the model is set with parameters similar to 39N0 in scale as follows:σ=0.0445 N·m?1,ρ=1×103kg·m?3,h=1.3×10?3m,andh′=8.5×10?4m.Compared with natural frequencies of four modes obtained accurately by Strauch Met al.,[11]where they observed all the frequencies except 17.95 Hz of mode(1,1)and 209.25 Hz of mode(0,3),the frequenciesf1–f4of the rest four modes have a good match with our analysis and the error is no more than 4.90%,as shown in Table 1.
When the frequency is low,the transmission beam cannot form interference superposition at the interface with a discontinuous standing wave, so the interference fringes cannot be observed. When the frequency is higher than 200 Hz,the liquid surface no longer vibrates conspicuously due to the inertia of the liquid, and the interference fringes cannot be formed either.
The errors in Table 1 may be caused as follows. Firstly,the cavity of commercial Varioptic 39N0 liquid lens is actually in the shape of a conical frustum,which is designed not only to increase the range of contact angle variation,but also to minimize the center deviation of the L–L interface while enhance its imaging stability. For the conical frustum model,spherical coordinates are more accurate than the cylinder coordinates.Secondly,in order to improve the response speed,the viscosity of the oil solution is modulated generally to make the oscillation of the interface near critical damping. Moreover,the viscosity dissipation of the interface and the friction at the side wall both have effects on the interface fluctuation.For simplicity of analysis,all those effects are ignored here. Therefore,to obtain more accurate results,hydrodynamic analysis should be carried out in spherical coordinate system under the influence of viscous damping and side wall friction.
In addition,the linear wave condition is no longer applicable when the amplitude of the wave is large at low frequencies. The condition that the amplitude is much smaller than the wavelength cannot be satisfied,and the nonlinear theory is needed.

Table 1. Comparison with the experiments in four modes.
3.2. Simulation analysis
3.2.1. Influence of lens radius on eigenfrequency
Curves in Fig. 2 are natural frequencies of each mode plotted with the lens radius according to Eq. (14). As the lens radius increases, the natural frequencies of modes 0 and 1 decrease,which means the smaller the lens is,the higher the natural frequencies are. Theoretically, the higher frequency modes are difficult to be measured due to the influence of inertia of the liquid,while the resonant modes of them at lower frequencies can be observed easily. Compared with the experimental results,curves in Fig.2 can be observed easily except mode(0,3)with the highest eigenfrequencies and mode(1,1)with the lowest eigenfrequencies.
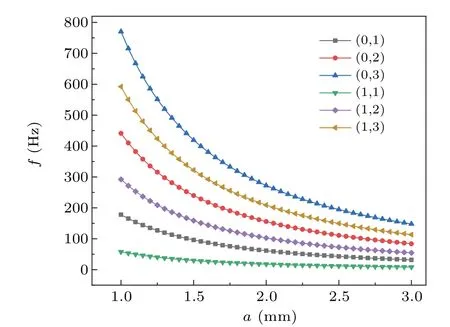
Fig.2. Natural frequencies of modes 0 and 1 changing with radius a.
3.2.2. Influence of liquid height ratio on eigenfrequency
The radius of the lens is fixed asa=1.95×10?3m,and the height of the lens is fixed asH=h+h′=3×10?3m,which is set to be a little larger than the actual height of 39N0 for larger range of variation.We take the ratio of ionic solution height to total heighth′/Has the variable,and each of the first three intrinsic frequencies inm=0 andm=1 are shown in
Fig.3. With the increase of the height of the ion solution,the natural frequencies increase and tend to be constant when the ratioh′/His close to 0.5.If the range of the horizontal axis extends to 1 in Fig.3,we will get symmetrical arch curves with the central symmetry point 0.5,as can be seen from Eq.(14).
Because we ignore the viscosity of the oil, and the two liquids have the same density, the height of the ion waterh′and the height of the oilhhave the same effect on the eigenfrequency of the lens, which can be seen from Eq. (14). So when the variable is set to beh/H, the curves are exactly as the same as Fig.3.When either of the liquid is lower,its height will have more effect on the natural frequencies.

Fig.3. Natural frequencies of modes 0 and 1 changing with ratio h′/H.
3.2.3. Influence of height-to-diameter ratio on eigenfrequency
If the two liquids have the same height,h′=h, and we take the height-to-diameter ratioh′/aas the variable, each of the first three intrinsic frequencies in modes 0 and 1 are analyzed,as shown in Fig.4. With the increase of the ratioh′/a,the natural frequencies increase and tend to be constant when the ratio exceeds 0.5. In other words, the flatter the cylinder is, the effect of the liquid height on the eigenfrequencies is greater. As the same as before, if the variable set to beh/a,the curves are the same as those shown in Fig.4.

Fig.4. Natural frequencies of modes 0 and 1 changing with ratio h′/a.
In conclusion,for a liquid lens of a flat cylinder with twolayer, the larger the radius is, the lower the intrinsic frequencies are; the larger the height difference of the two liquids is,the lower the eigenfrequencies are;and the smaller the heightto-diameter ratio of the lens is,the lower the intrinsic frequencies are.
4. Conclusion
An approximate model of a commercial electrowetting liquid lens is established,and the analysis of the capillary wave in the lens is carried out. Based on hydrodynamics,the analytical expression for the natural frequency of the lens has been derived in cylindrical coordinates. The results are in good agreement with the experiments in previous literature. This study provides a basis for the use of dynamic response of the lens,such as response time optimization,optical space modulation,optical communication encryption and many other applications.
- Chinese Physics B的其它文章
- Physical properties of relativistic electron beam during long-range propagation in space plasma environment?
- Heterogeneous traffic flow modeling with drivers’timid and aggressive characteristics?
- Optimized monogamy and polygamy inequalities for multipartite qubit entanglement?
- CO2 emission control in new CM car-following model with feedback control of the optimal estimation of velocity difference under V2X environment?
- Non-peripherally octaalkyl-substituted nickel phthalocyanines used as non-dopant hole transport materials in perovskite solar cells?
- Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study?

