考慮連接性的三明治阻尼復合結構拓撲優化設計
張 橫 丁曉紅 沈 磊 徐世鵬
上海理工大學機械工程學院,上海,200093
0 引言
航天航空、航海等工程裝備日益向高速重載方向發展,三明治結構由于具有多功能性的特點被廣泛應用于這些工程裝備中。這些工程裝備在工作中經常承受動態載荷,容易引發結構振動噪聲問題,如潛艇的隱身性能與艦體的振動噪聲息息相關,減小艦體的振動噪聲可以有效提高潛艇的隱身性能。為保證這些裝備能夠正常有效工作,通常要將結構的振動水平控制在某一范圍內。結構振動控制通常采用主動控制和被動控制方法。被動控制方法由于其可靠性高、可控頻帶寬等優點,成為結構振動噪聲控制的有效方法,其中在結構上施加阻尼材料,通過提高結構阻尼來達到減振目的是一種行之有效的措施。另外,結構還需要保證高剛度特性,以滿足承受載荷的需求。
三明治阻尼復合結構的宏觀性能與中間阻尼層材料的性能息息相關,針對高剛度高阻尼的設計要求,有效且直接的方法是設計阻尼復合材料的微結構。為了實現高剛度高阻尼,阻尼復合材料在微觀結構上可由兩相材料組成,一相為剛度較大的材料,用于保證結構的剛度,另一相為阻尼較大的材料,用于提高結構的阻尼。通過對這兩相具有競爭性的材料進行拓撲優化設計,可以得到高剛度高阻尼的三明治阻尼復合結構。
針對材料微結構設計問題,SIGMUND[1-2]提出了基于逆均勻化方法的材料微結構設計方法,實現了材料特定剛度和負泊松比設計。對于阻尼復合材料的設計,YI等[3-4]研究表明,微觀拓撲形態的改變可以提高黏彈性復合結構的剛度和阻尼性能,并通過將逆均勻化方法[1-2]應用于阻尼復合材料的設計中,實現了以提高阻尼復合材料剛度和阻尼性能為目標的微結構設計。ANDREASSEN等[5]針對阻尼復合材料不同的微結構形式對材料的帶隙特性的影響進行了研究。CHEN等[6]對阻尼材料剪切模量和阻尼因子之間的關系進行了研究,并通過對剪切模量進行優化設計,來提高結構阻尼。ANDREASEN等[7]以提高結構阻尼性能為目標對黏彈性復合材料的微結構進行了優化設計。HUANG等[8]研究了阻尼復合材料設計中目標問題,對比了分別以剛度和阻尼為設計目標時微結構的構型問題。
針對以結構宏觀性能為目標的微結構設計問題,CHEN等[9]分別以結構第一階阻尼比、第二階阻尼比、第三階阻尼比和前三階加權阻尼比加權和為目標對約束阻尼層結構的微結構問題進行設計研究,結果表明,在這4種設計目標下,當體積分數為0.4和0.5時微結構的構型基本相同。YUN等[10]針對動態載荷作用下三明治阻尼復合結構中的阻尼層進行了微結構優化設計研究,設計結果表明,進行微結構設計后整體結構的振動響應大幅減小。LIU等[11]在考慮結構頻率約束情況下對阻尼復合結構的微結構進行了設計,優化后結構的振動響應相較于經驗設計明顯減小。ZHANG等[12]研究了阻尼復合結構的多尺度設計問題,研究表明阻尼復合材料可以有效提高結構阻尼、減小振動響應。
盡管對阻尼復合材料進行微結構設計可以有效提高材料阻尼性能,達到減振的目的,但是通常以阻尼為目標的阻尼復合結構設計中[4-5,7-8,12],都是阻尼較大相材料保持連接性,剛度相被分割為孤島,這主要是因為阻尼相連接能保證結構的虛部較大、實部較小,從而可以有效提高結構的阻尼,但是這種結構不利于后續的加工制造。ANDREASEN等[5]研究發現,通過剛度約束并不能保證微結構的連接性。HUANG等[8]研究表明,以阻尼因子為目標可以有效提高材料阻尼性能,微結構中阻尼材料保持連接性;而以剛度為目標可以保證微結構中剛度相材料保持連接,但是微結構的阻尼性能較差。
為了提高結構的可制造性,需要研究考慮制造約束的三明治阻尼復合結構的設計方法。針對連接性設計問題,ZHOU等[13]采用強制性連接約束法、虛載荷法和非線性擴散法針對單相材料進行了設計和比較,由于是單相材料,微結構構型的連接性變化對設計目標的影響較小;對于由性能相反的兩相材料構成的微結構而言,材料的構型變化對目標函數和設計約束有很大的影響,無法直接采用上述方法解決微結構的連接性約束設計問題。本文提出通過組合強制性約束法和非線性擴散法的新方法,來實現具有剛度相連接的兩相材料阻尼復合結構的最大阻尼設計。
1 三明治阻尼復合結構計算模型
為實現三明治阻尼復合結構的連接性優化設計,需要首先建立三明治阻尼復合結構的計算模型,并進行有限元分析。
1.1 三明治阻尼復合結構
為了確保結構的可加工性要求,需要對結構中易加工相材料進行連接性約束設計。兩相材料分別為鋁合金和環氧樹脂,在三明治阻尼復合結構制造中,可事先將鋁合金部分通過3D打印或者其他方式加工出來,然后將另外一相澆筑進去,即可得到最終的三明治阻尼復合結構。圖1a所示為三明治結構,其中,中間層為阻尼層,上下層為金屬層。對阻尼層進行微結構設計,使微結構中剛度相材料與上下表層相連接,這樣可以整體打印出上下表層及阻尼層的剛度相材料,最終得到圖1b所示的連結性結構。

(a)三明治結構

(b)連接性剛度相材料圖1 三明治結構及其連接性描述Fig.1 Sandwich structures with connectivephase material
1.2 結構模態阻尼比的計算
阻尼材料的阻尼特性使用復模量表示,公式如下(本文不考慮阻尼材料性能隨溫度和頻率而改變特性的情況):
E=E′+jE″=E′(1+jη)
(1)
式中,E′、E″和η分別為黏彈性材料的儲能模量、損耗模量和材料損耗因子;j為虛數單位。
結構自由振動的運動微分方程為
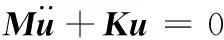
(2)
其中,u為位移向量,M和K分別是結構質量矩陣和剛度矩陣,由于阻尼材料模量的復數形式,可知K為復剛度矩陣,表達式為
K=Kp+Kv=KR+jKI
(3)
這里,Kp和Kv分別為上下金屬層和阻尼層的剛度矩陣。上角標“p”和“v”分別代表金屬層和阻尼層。KR和KI分別為復剛度矩陣的實部和虛部,其表達式分別如下:
KR=Kp+ReKv
(4)
KI=ImKv
(5)
基于模態應變能法[14]計算結構的第k階模態阻尼比可表達為
(6)
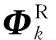
2 優化數學模型及靈敏度分析
2.1 連接性約束
以阻尼為目標的設計通常都會得到高阻尼材料相互連接的結構,但是這樣的結構很難制造。考慮到微結構中剛度相材料的連接性,通過組合強制性連接約束法和非線性擴散法實現。強制性連接約束通過選定部分非設計域來實現,三明治結構上下表層與阻尼層中剛度相材料連接,考慮將單胞的四角點作為強制性連接約束的非設計域,如圖2所示。
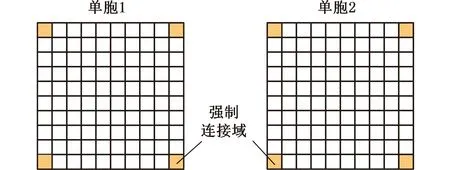
圖2 強制性連接約束示意圖Fig.2 Schematic of kinematical connectiveconstraints method
非線性擴散可以有效抑制棋盤模式和模糊邊界,確保適當的拓撲互連。從理論上講,密度梯度發生在材料交界處,因此,最小化密度梯度的范數可以有效避免非連接的發生。非線性擴散方程可以表示為
?tx=div(D×x)
(7)
式中,D為擴散張量;x為對應的質量濃度,也就是材料密度;t為尺度參數,如時間系數。
擴散過程的性質由擴散張量決定,當D為單位矩陣時,擴散過程沿四周均勻進行,如熱傳導方程;當D是結構密度差分的函數形式時,就形成了非線性擴散:
?tx=div(g(|x|2)x)
(8)
其中,g(│x│2)為擴散函數,引入一個勢函數,使其梯度與擴散函數有如下關系:
φ(|x|)=g(|x|2)x
(9)
在變分法中,非線性擴散可以被描述為能量的形式,因此,形成非線性擴散方程的能量泛函最小化可以表示為
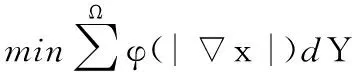
(10)
其中,Y為微結構的設計域。為使結構內部連續性良好,應滿足內部材料單元密度梯度│x│盡可能小,盡量接近線性擴散;同時,為了保證結構邊界清晰,應滿足密度擴散沿著邊界的切向進行,而避免沿著法向穿過邊界擴散。因此,需選用合適的φ(│x│),根據上述要求,本文中選取φ(s) =s/(1+s2)。
2.2 優化數學模型
為了最大化結構的阻尼性能,考慮以結構的模態阻尼因子為目標對結構進行優化設計;同時為了考慮微結構中剛度相材料的連接性,基于非線性擴散法,將結構整體密度梯度的能量泛函加權至模型目標函數中,得到優化設計的數學模型:
findX(xi)
(11)
(12)
(13)
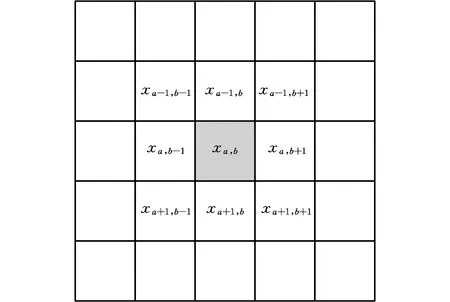
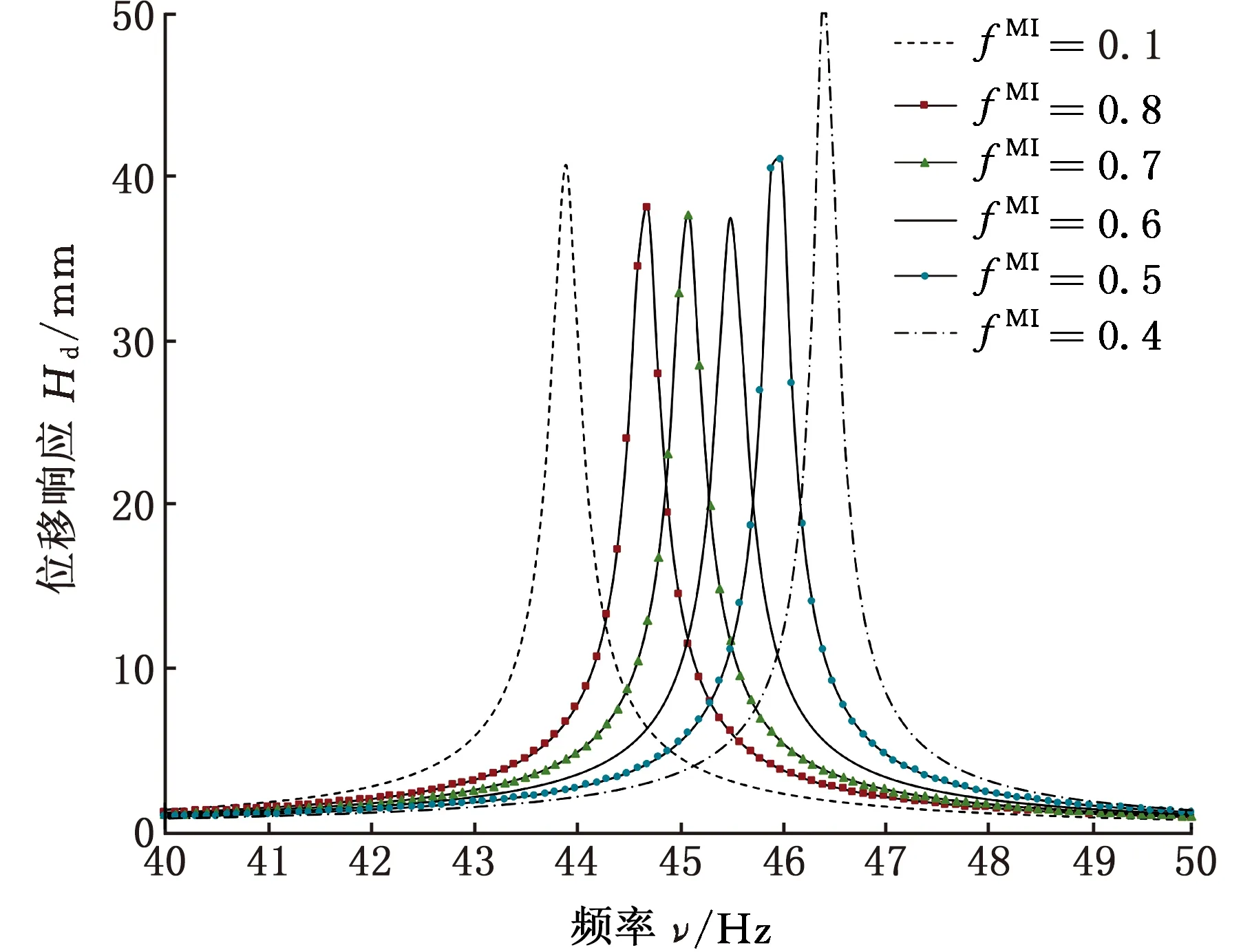
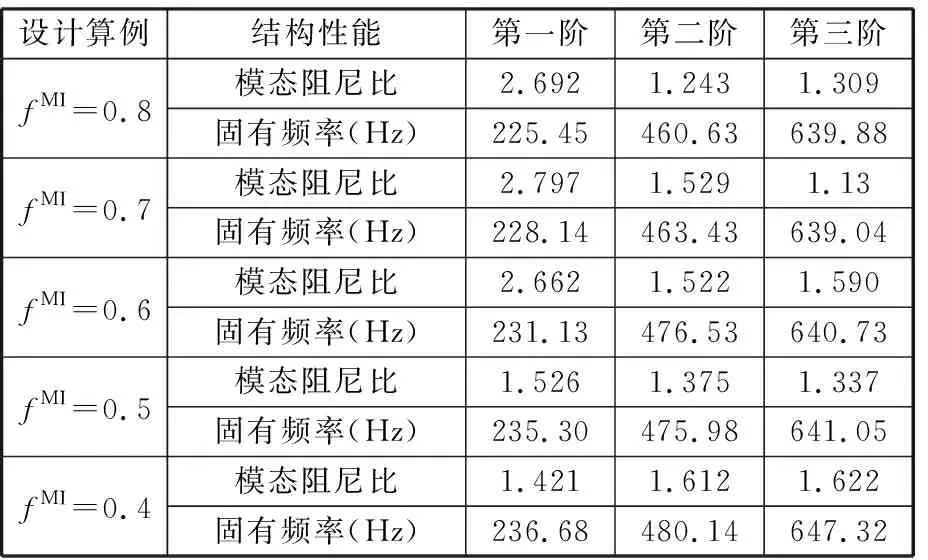
0 (14) 其中,X是設計變量,即復合阻尼材料微結構設計變量xi。式(12)為目標函數,第一項為結構阻尼目標函數,wk為第k階模態阻尼比的權重,當kmin=kmax時, 僅對結構第k階模態阻尼比進行優化,當kmin 在以結構宏觀性能為目標的微結構設計模型中,對微結構單元的靈敏度分析要建立在對結構宏觀性能分析的基礎上。在宏觀尺度上對結構進行有限元分析,計算出整體結構的性能,然后通過將宏觀性能目標對微結構設計變量求導,即可得到微結構設計單元的靈敏度。阻尼復合材料微結構單胞的等效彈性矩陣DH為 (15) 式中,ui為微結構中第i個單元的位移場;│Y│為微結構單胞的體積;Y為微結構的設計域,Yi為單胞上第i個單元的體積;I為單位矩陣;b為應變位移矩陣;DMI為微結構上第i個單元的彈性矩陣。 為了獲得清晰的設計結果,基于SIMP插值方法,微結構上第i個單元彈性矩陣的插值模型為 (16) 式中,p為懲罰系數,本文中p=3;D1和D2分別為剛度相材料和阻尼相材料的彈性矩陣。 根據式(15)和式(16),可得優化過程中復合阻尼材料的等效復彈性矩陣DH為 (17) 對于式(12)目標函數的靈敏度分析,可分別對兩項進行求導再相加。第一項對設計變量靈敏度可通過式(6)對設計變量xi求導得到 (18) 其中,剛度矩陣Kv為 (19) 式中,B應變位移矩陣;n為結構阻尼層劃分的單元數;Ω為單元體積。 通過式(19),可得式(18)中Kv的虛部和實部對設計變量xi的靈敏度分別為 (20) (21) 等效彈性矩陣對設計變量xi為 (22) (23) 將式(22)和式(23)分別代入式(20)和式(21),復合阻尼材料剛度矩陣虛部和實部對設計變量的靈敏度分別為 (24) (25) 將式(24)和式(25)代入式(18),可得到結構第k階模態阻尼因子對微觀結構設計變量的靈敏度。 目標函數第二項對設計變量的靈敏度為 (26) 當對設計域劃分單元后,設xi在總體結構中的位置為圖3所示的xa,b位置,則與其相鄰的單元分別為xa-1,b、xa+1,b、xa,b-1、xa,b+1,如圖3所示。根據散度的定義可得 圖3 鄰接單元示意圖Fig.3 Adjacent element div(g(|xi|2)xi)=w1xa-1,b+w2xa+1,b+ (27) (28) (29) (30) (31) 將式(27)代入式(26)即可得到目標函數中第二項對設計變量的靈敏度。 考慮連接性的三明治阻尼復合結構拓撲優化設計方法的主要設計步驟如圖4所示,包括如下幾個設計步驟: 圖4 優化設計流程Fig.4 Flowchart of the proposed topologyoptimization procedure (1)初始模型的建立。建立優化的幾何模型,阻尼層設置為可設計域,其他為非設計域。 (2)微結構的有限元分析。對復合阻尼材料微結構進行網格劃分,建立有限元模型,除四角點外所有單元設置為設計變量。通過式(17)計算單胞的等效復彈性矩陣DH。 (3)結構宏觀性能有限元分析。使用步驟(2)得到的復合阻尼材料的等效復彈性矩陣DH計算整體結構的性能。 (4)靈敏度分析。使用式(18)和式(26)計算設計變量xi的靈敏度。 (5)使用移動漸近線法[15](method of moving asymptotes,MMA)更新設計變量。MMA方法是一種基于梯度的迭代尋優算法,通過引入移動漸近線,將隱式的優化問題轉化成一系列顯式的、可分離的、嚴格凸的近似子優化問題。每一步迭代中,通過用梯度類算法求解凸近似子問題來更新設計變量,適于處理目標函數復雜且具有多約束的拓撲優化問題。 (6)收斂判斷。如果優化迭代的目標函數連續兩次的差值小于收斂容差,或者迭代次數到達設定的最大值N,則退出循環,否則返回繼續迭代,直到達到收斂條件。 為了驗證所提設計方法的有效性,對兩個不同邊界條件的三明治阻尼復合結構進行拓撲優化設計,第一個為懸臂結構,第二個為兩邊固支結構。材料具體參數如表1所示。微結構優化中選取圖5所示的構型,初始密度為微結構中體積分數設定值,四角點初始密度設置為0.001(鋁合金),且迭代過程中保持不變,作為強制性連接約束。微結構劃分為40×40個單元。 圖5 初始微結構構型Fig.5 Initial guess microstructure 表1 材料屬性 懸臂結構如圖6所示,長1500 mm,總厚度為100 mm,上下表層厚度分別為25 mm,阻尼層厚度50mm。基板和阻尼材料參數如表1所示,結構左側固定約束,構成懸臂板。 圖6 懸臂結構Fig.6 A cantilever structure 為了研究阻尼材料在微結構中所占的體積分數對設計結果的影響,以結構前三階模態阻尼比加權最大為目標,通過設置不同的體積約束條件對懸臂結構進行拓撲優化設計。圖7所示為微結構不同阻尼材料體積分數約束下的設計結果,可以看出,不同體積分數下微結構的構型形態相似,都是“1”字形,隨著體積分數的增大,阻尼材料的分布逐漸變寬,微結構等效彈性模量的實部和虛部都逐漸減小。表2所示為不同體積分數設計結果的模態頻率和模態阻尼的對比,從表中可知,隨著阻尼材料體積分數的增大,結構的頻率逐漸減小,同時結構的阻尼逐漸增大,但是阻尼增大的幅度越來越小。圖8所示為不同體積分數設計結果在第一階模態頻率處的頻率響應對比,激勵點和響應點都為懸臂結構右上角點。從圖中頻率響應曲線可得,結構的頻率響應隨著阻尼材料體積分數的增加先是逐漸減小,當fMI=0.6時達到最小值后,隨體積分數的增大響應逐漸變大。由此可得,當微結構種阻尼材料的體積分數為0.6時結構的性能最優。 表2 不同體積分數設計結果性能對比 (a)fMI=0.4時設計結果 (b)fMI=0.5時設計結果 (c)fMI=0.7時設計結果 (d)fMI=0.8時設計結果圖7 不同微結構體積分數設計結果Fig.7 Design results with different volume fractions 因為目標函數中加權了密度梯度的能量,所以設計問題已不再是純粹的以阻尼比最大為目標的設計問題。文中以第k階模態阻尼比為目標時并不會使設計結果的第k階模態阻尼比是最優的,因此可認為設計結果性能的優劣對目標函數中模態阻尼比階次的選取相關性較小。 圖8 不同體積分數設計結果頻率響應對比Fig.8 The simulated frequency response of thedifferent design result 為了進一步驗證本文所提方法的有效性,對設計結果進行實驗驗證。考慮到成本以及測試精度,采用縮小的比例模型對三明治結構進行實驗,長度和寬度方向縮放比例為1∶10,厚度方向為5 mm(易于粘貼加速度傳感器的最小尺寸)。采用3D打印技術,分別打印阻尼材料體積分數為0.4、0.5、0.6、0.7和0.8的模型,打印后結構的尺寸為165 mm(長) ×6 mm(寬) ×10 mm (高),如圖9所示。三明治阻尼復合結構的制造過程如下:首先通過3D打印技術打印出具有連接性的鋁合金相結構,然后將環氧樹脂填充于打印好的金屬結構中,即可完成三明治阻尼復合結構的制造。 (a)三明治阻尼復合結構試件 (b)圖a局部放大圖(c)單胞示意圖圖9 制作的三明治阻尼復合結構試件Fig.9 The 3D printed sandwich composite structures 采用對比試驗方法,在相同的實驗條件下對不同的試件進行測試,以此來對比不同結構性能的優劣,圖10為實驗布置圖,具體測試流程如下: (1)邊界條件的施加。通過夾具將結構一端夾持來模擬懸臂結構。 (2)實驗測試。通過錘擊法對結構進行模態實驗,錘擊點如圖10中箭頭所指的點所示,拾取自由端響應。通過測試得到試件的模態頻率和模態阻尼比,如表3所示。表3與表2的結果有所不同,主要原因在于對算例進行優化設計時使用的是平面應力單元,結構的厚度為1 mm,由于厚度較小,制作的試件很難粘貼傳感器進行測試,因此在厚度方向上加大了結構尺寸;同時結構尺寸較大,不便于制作,采用模型實驗對結構進行測試,盡管樣件與仿真算例有所不同,但是實驗都是在相同的條件下進行的,實驗結果仍能夠反映優化設計結果的性能。從表3中可知,隨著阻尼材料體積分數的減小,結構的前三階頻率逐漸增大,結構的前三階模態阻尼逐漸減小,這與表2所示的仿真結果趨勢相同。試件在第一階模態處的頻率響應如圖11所示,由圖可知,隨著微結構阻尼相體積分數的增大,結構的頻率響應隨微結構阻尼相體積分數呈現非線性變化,隨著體積分數增大,結構在第一階模態處的頻率響應依次為32.42g/N、29.40g/N、20.64g/N、21.22g/N、23.27g/N,結構響應首先逐漸減小,當體積分數為0.6時響應值最小,隨后隨著體積分數的增大,結構的響應逐漸增大。這主要是因為結構的頻率響應與結構的剛度和阻尼同時相關,以犧牲結構剛度為代價獲得更大的阻尼并不能有效減小結構的響應。對于復合結構而言,存在一個最優的剛度和阻尼使得結構的響應最小。 圖10 實驗布置圖Fig.10 Experimental setup 表3 不同試件實驗測試結果 圖11 實驗測試頻響函數Fig.11 The experimental frequency response of thedifferent design result (1)本文提出了一種考慮連接性的三明治阻尼復合結構拓撲優化設計方法,通過組合強制性連接約束和非線性擴散法,實現了對阻尼復合結構的連接性設計,并結合3D打印技術實現了三明治阻尼復合結構的材料-結構-設計-制造協同優化。優化后的結構阻尼變大,結構的頻率響應變小。 (2)在考慮微結構連接性時,因在阻尼目標函數中加權了密度梯度的泛函,所以不同阻尼比目標函數下得到的設計結果的性能差異較小,目標函數的選擇對設計結果的影響很小。 不同體積分數的仿真和實驗結果表明,在微結構上存在最優的阻尼材料體積分數使優化后的結構頻率響應最小。2.3 靈敏度分析

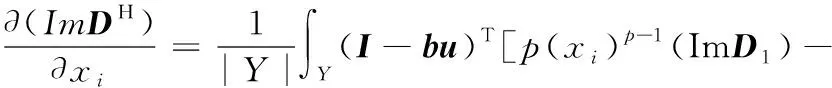
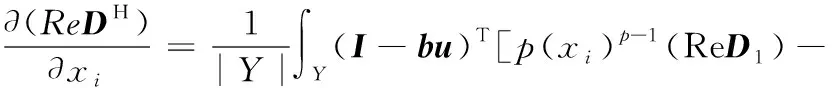
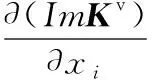
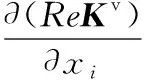
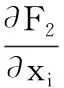
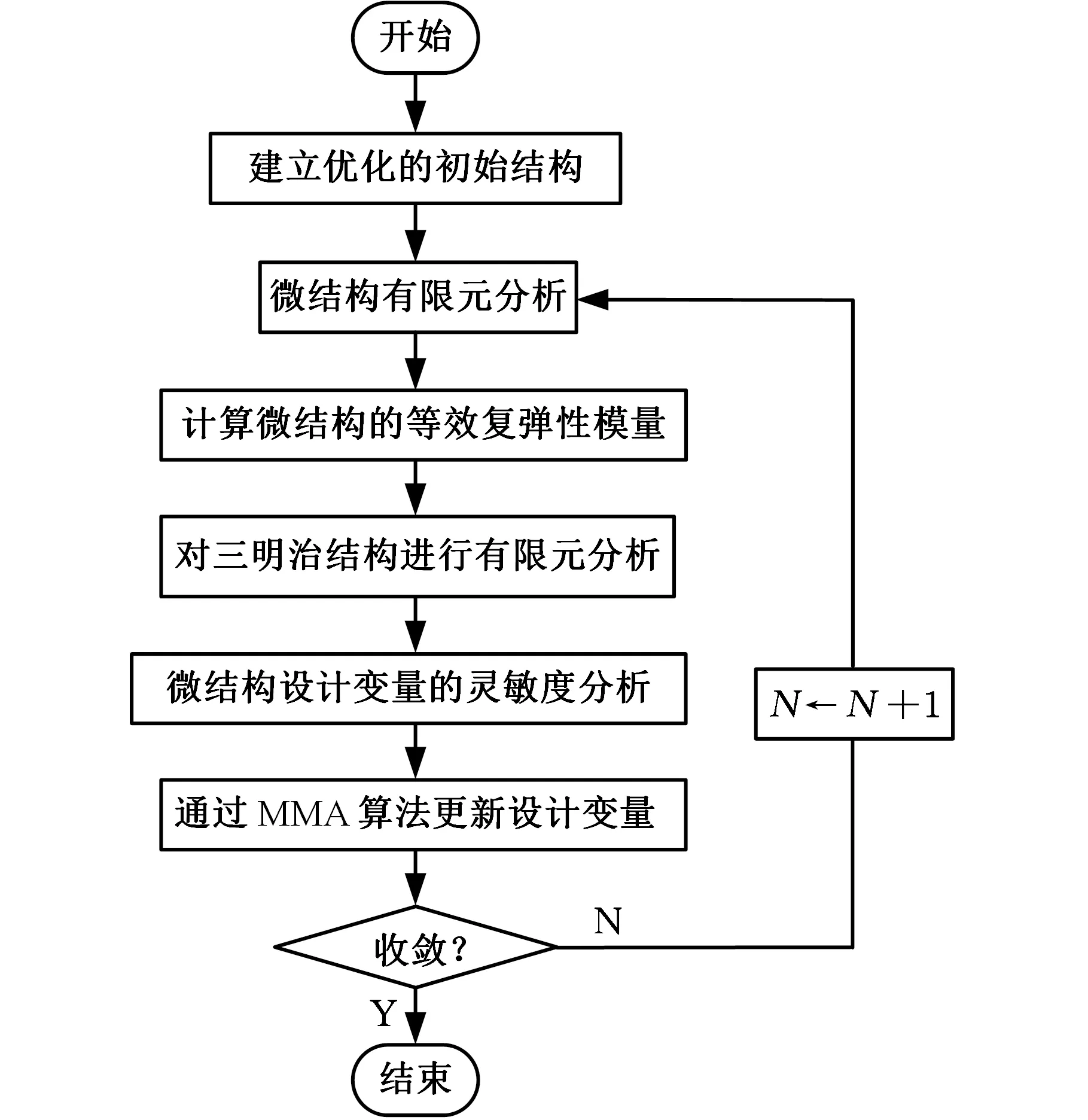
2.4 優化設計流程
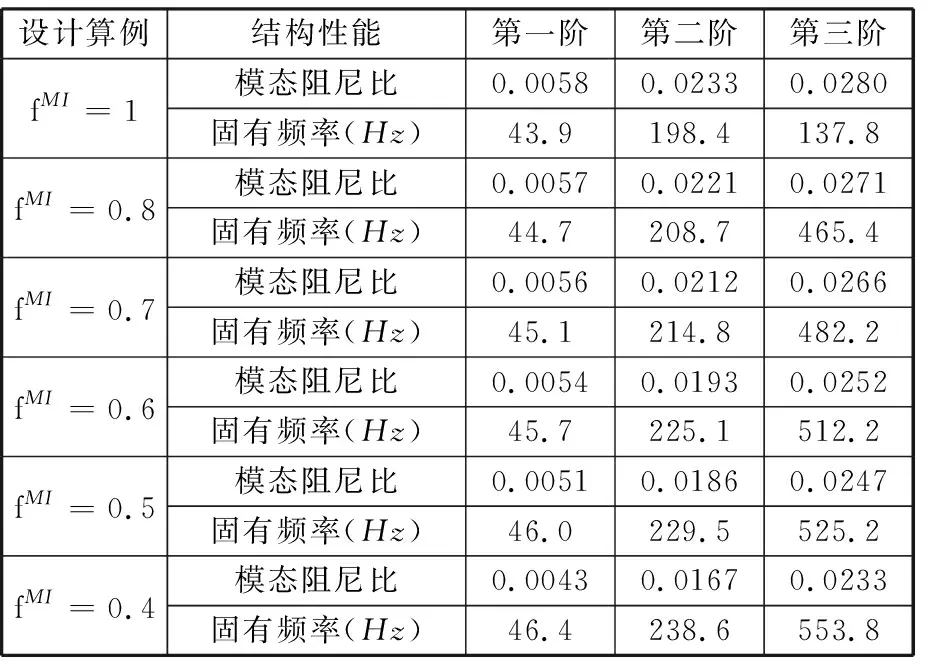
3 數值算例







4 實驗驗證



5 結論

