動態加權條件互信息的特征選擇算法

張 俐 陳小波

①(江蘇理工學院計算機工程學院 常州 213001)

②(北京郵電大學可信分布式計算與服務教育部重點實驗室 北京 100876)

③(中國人民銀行常州市中心支行 常州 213001)

1 引言

在過去幾十年里，新型計算機和互聯網技術正在以前所未有的速度產生著大量高維數據[1,2]。在這些高維數據中包含著許多無關和冗余特征。因為不相關和冗余特征不僅會增加模型訓練時間而且也使得模型的可解釋變得很差。如何處理這些不相關和冗余特征是數據分析和知識發現中所面臨的重大挑戰。特征選擇不同于其他數據降維技術(如特征提取)[3]，它可以刪除無關和冗余特征，保留相關原始物理特征，從而降低數據維數。這樣有利于提高數據質量和分類性能，并使得模型的訓練時間大幅縮小而且也使得模型的可解釋性變得更強[4,5]。

通常特征選擇技術又分為分類依賴型[6](包裝器方法和嵌入式方法)和分類器無關型(過濾式方法)。基于信息論的過濾式特征選擇方法優點[7–11]為：(1)它可以直接從數據中提取有價值的知識，而且這些知識對于問題真正的解決又起到至關重要作用。(2)它的計算成本低且與具體分類器無關。(3)目前該方法應用領域廣泛，包括基因表達數據、文本分類和網絡入侵檢測等多個領域。因此基于信息論的過濾式特征選擇方法逐漸成為特征選擇技術的研究熱點[12–16]。

常見基于信息論的特征選擇算法[5,17–19]可分為兩類。最小化冗余特征的算法(maxMIFS[8]，MRMR[20]，CIFE[8]，CMIM[8]和JMI[10]等)和最大化新分類信息的算法(DCSF[12]和JMIM[16])。maxMIFS和MRMR通過去除特征之間冗余特征來提高最優特征子集(S)整體識別質量。但是它們卻忽視兩個特征與類標簽之間的冗余性問題。因此，產生許多經典的多信息去除冗余性的算法，例如JMI,CIFE和CMIM等。然而它們卻忽視最大化新分類信息來提高S集合整體識別的質量。隨著特征選擇算法的發展，如何將減少冗余的特征選擇算法和最大化新分類信息的特征選擇算法進行融合逐漸成為研究的新熱點。代表性的算法有MRI[13],CFR[14]和DISR[21]等。以上這些算法都是基于信息論特征選擇框架[7]的具體實現。Brown等人[7]認為選擇不同的參數就是選擇不同的特征選擇算法。它們存在的問題是參數設置過大還是過小都會對特征選擇過程造成影響，即存在對無關特征和冗余特征的忽略與誤判。

在大數據環境下，針對數據多樣性和高維性的特點，尋找一種動態的非預先設置參數的特征選擇方法就成為目前需要解決的問題。本文提出一種新的過濾式特征選擇算法(Weighted Maximum Relevance and maximum Independence,WMRI)。本文主要貢獻為：(1)利用條件互信息衡量特征與類標簽之間的相關性以及特征之間冗余性；(2)提出通過均值和標準差來動態調節新分類信息和保留類別信息的權重與平衡問題；(3)通過對10個基準數據集進行實驗對比，實驗結果表明，該算法(WMRI)優于其他特征選擇算法(DCSF,MRI,CFR,IG-RFE[15]和JMIM)。

2 WMRI算法的提出

Brown等人[7]提出基于信息論特征選擇框架，具體為

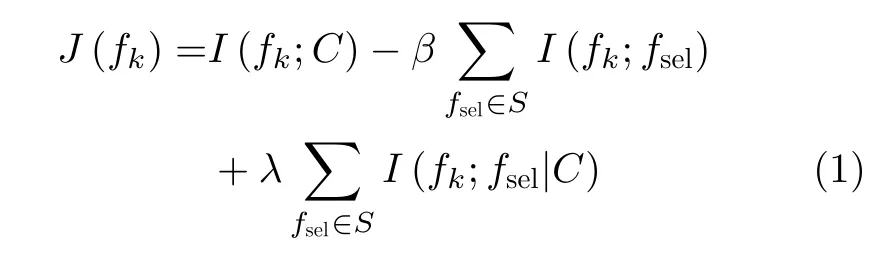
其中，設F是原始特征集合，|S|是最優特征子集數，S ?F,J(·)代表評估標準，fk表示候選特征，fsel表示已選特征，fsel∈S,fk∈F-S,C表示類標簽集合，|C|是類標簽數。

Wang等人[13]在Brown的研究基礎上提出MRI算法，具體評估標準為

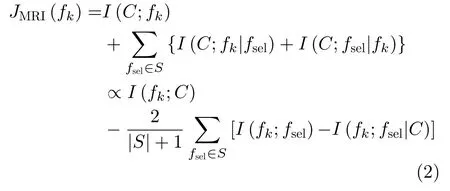
從式(2)中可知，在MRI算法中，獨立分類信息由新分類信息項I(C;fk|fsel)與保留類別信息項I(C;fsel|fk)構成，并且這兩種分類信息同等重要，存在問題是在實際中I(C;fk|fsel)與I(C;fsel|fk)之間存在差異性。同時，結合式(1)和式(2)又可知該算法存在預先設置參數β和λ的問題，即λ=。

那么，如何在不增加計算量和復雜度的情況下，動態區分新分類信息和保留類別信息之間的重要程度。以適應在大數據環境下，數據多樣性和高維性的特點，并提高S集合整體數據的質量，就成為目前在特征選擇領域中需要研究的一個問題。

本文提出一種新的過濾式特征選擇算法(WMRI)。該方法通過引入標準差方法來分別計算I(C;fk|fsel)與I(C;fsel|fk)之間的權重。因為標準差[2]是一種常見的測量系統穩定程度的度量方法。標準差值越高，表示分散度越高；反之亦然。因此，通過標準差可以動態平衡新分類信息項與保留類別信息項之間的重要程度。WMRI算法評估標準具體為

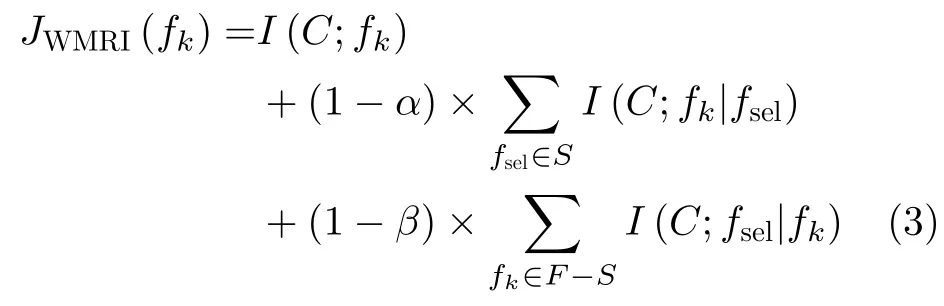
從式(3)可以得出，α和β可以分別動態測量新分類信息項I(C;fk|fsel)與 保留類別信息項I(C;fsel|fk)的重要程度。通過這樣，WMRI算法可以解決I(C;fk|fsel)項與I(C;fsel|fk)項之間平衡和權重問題。其中，式(3)中α和β分別由式(5)和式(7)表示，它的偽代碼如表1所示。

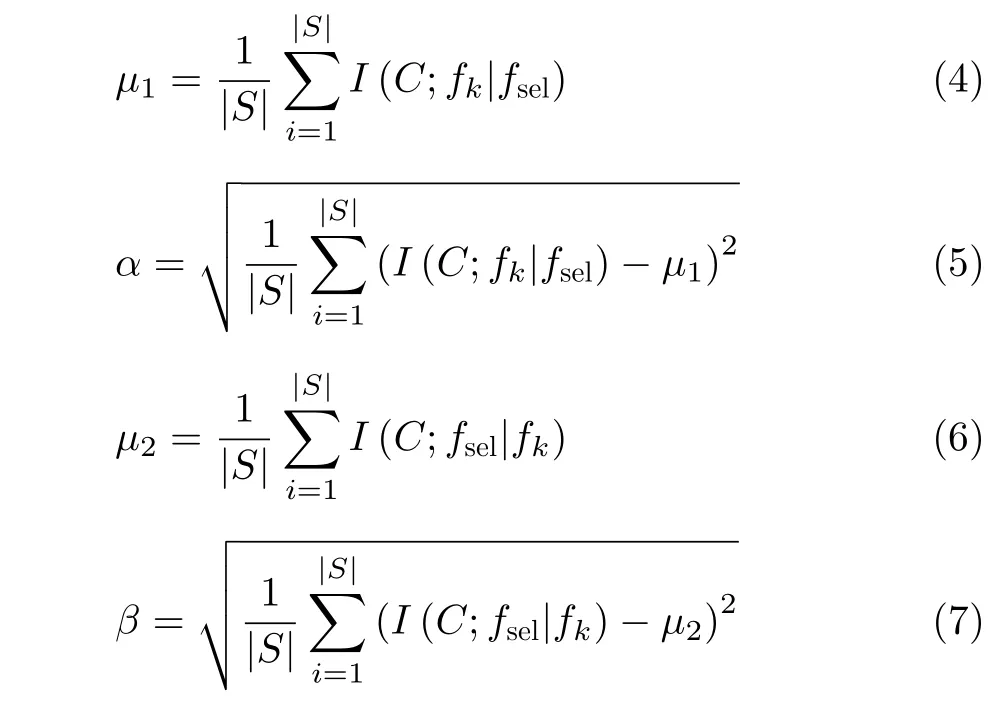
從式(3)可以知道，WMRI算法與MRI算法相類似，都采用前向順序搜索特征子集。通過表1可知，WMRI算法主要分為3部分。第1部分(第(1)～(6)行)主要包括：(1)初始化S集合和計數器k；(2)計算集合F中每個特征的互信息，選擇出最大的特征fk，將該特征fk從F集合中刪除，并將特征fk加入S集合，這時候選特征fk變成已選特征fsel。第2部分(第(7)～(15)行)主要是分別計算I(C;fk|fsel),I(C;fsel|fk),μ1,α,μ2和β的值。在第3部分(第(16)～(20)行)，根據式(3)的選擇標準，選擇出最大JWMRI(fk)值所對應的特征fk，并將該特征fk存入S并從F中刪除該特征fk，然后一直循環到用戶指定的閾值K就停止循環。

表1 WMRI算法的偽代碼

WMRI算法包括2個“ for”循環和1個“while”循環。因此，WMRI算法的時間復雜性是O(Kmn)(K代表已選特征數，n代表所有特征數，m代表所有樣本數，K?n)。WMRI算法復雜性高于MRI算法，IG-RFE算法，CFR算法，JMIM算法和DCSF算法。主要原因在于WMRI算法還需計算μ1,α,μ2和β的值。

3 實驗分析與討論

3.1 數據集描述

為了驗證所提出WMRI算法的有效性，在實驗中使用10個不同數據集進行驗證。這些數據集來自不同的領域，同時它們可以在UCI[13]和ASU[19]中找到。這些數據集包括手寫數字數據(Semeion和Mfeat-kar)、文字數據(CANE-9)、語音數據(Isolet)、圖像數據(COIL20和USPS)、生物學數據(WPBC和ALLAML)和其他類數據(Madelon和Musk2)。更詳細的描述可以在表2中找到。

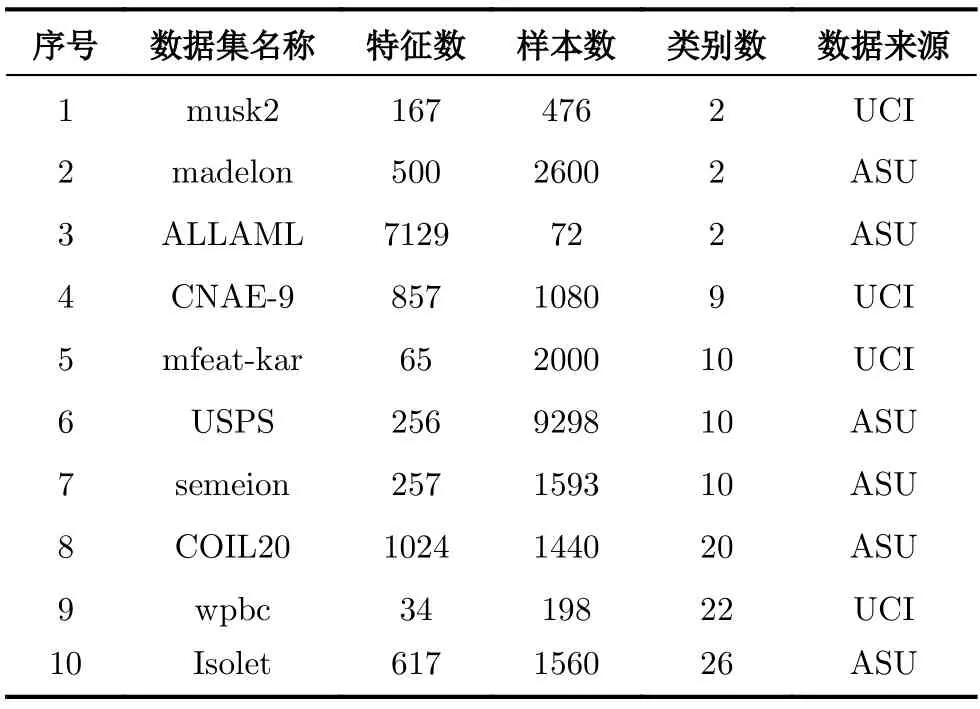
表2 數據集描述

3.2 實驗環境設置

在實驗中，使用K近鄰(KNN)[19]、決策樹(C4.5)[13]和隨機森林(RandomForest)[22]來評估不同的特征選擇算法。本文的實驗環境是Intel-i7處理器，使用8 GB內存，仿真軟件是Python2.7。

實驗由3個部分組成。第1部分是數據預處理。為保證實驗的公正性，整個實驗過程采用6折交叉驗證方法進行驗證，就是將實驗數據集均勻分成6等份，5份作為訓練數據集，1份作為測試數據集。第2部分是特征子集的生成。在實驗中，采用不同特征選擇方法生成特征子集。特征子集的規模設為30。第3部分是特征子集評價。在這個部分中，用fmi來評估分類器在特征子集上的分類準確率。分類準確率是指正確分類的樣本數占樣本總數的比例。設TP(True Positive)指正類判定為正類的個數；FP(False Positive)指負類判定為正類的個數；TN(True Negative)指負類判定為負類的個數；FN(False Negative)指正類判定為負類的個數。sen,prc和fmi定義分別為

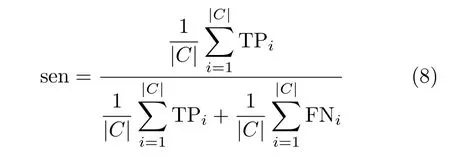
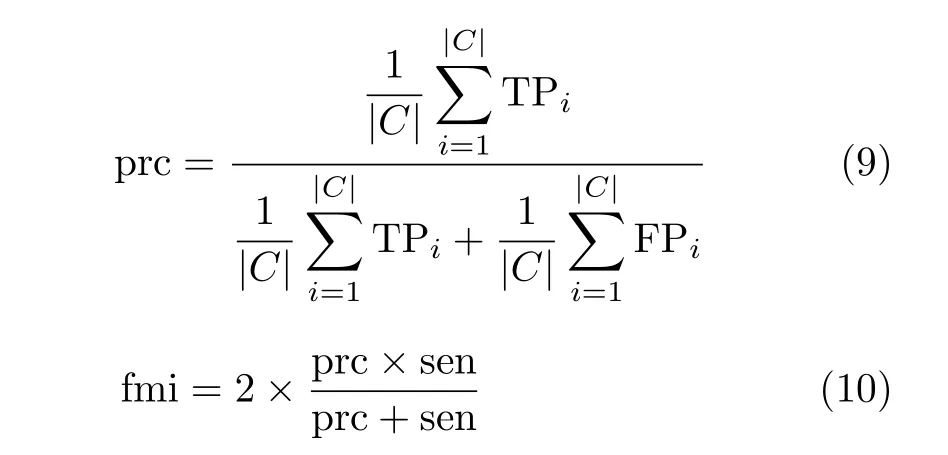
3.3 實驗結果與討論

表3—表5分別選擇KNN，C4.5和Random Forest這3種分類器，同時以fmi分類準確率作為評價指標對WMRI，IG-RFE，CFR，JMIM，DCSF和MRI進行統計分析。表中每行中最大值用黑體字標識。命名為“平均值”的所在行表示平均fmi值。通過使用“+”，“=”和“–”表示WMRI算法分別“優于”、“等于”和“差于”其他特征選擇算法。命名為“W/T/L”的所在行，分別表示WMRI算法與其他特征選擇算法的勝/平/負的次數。

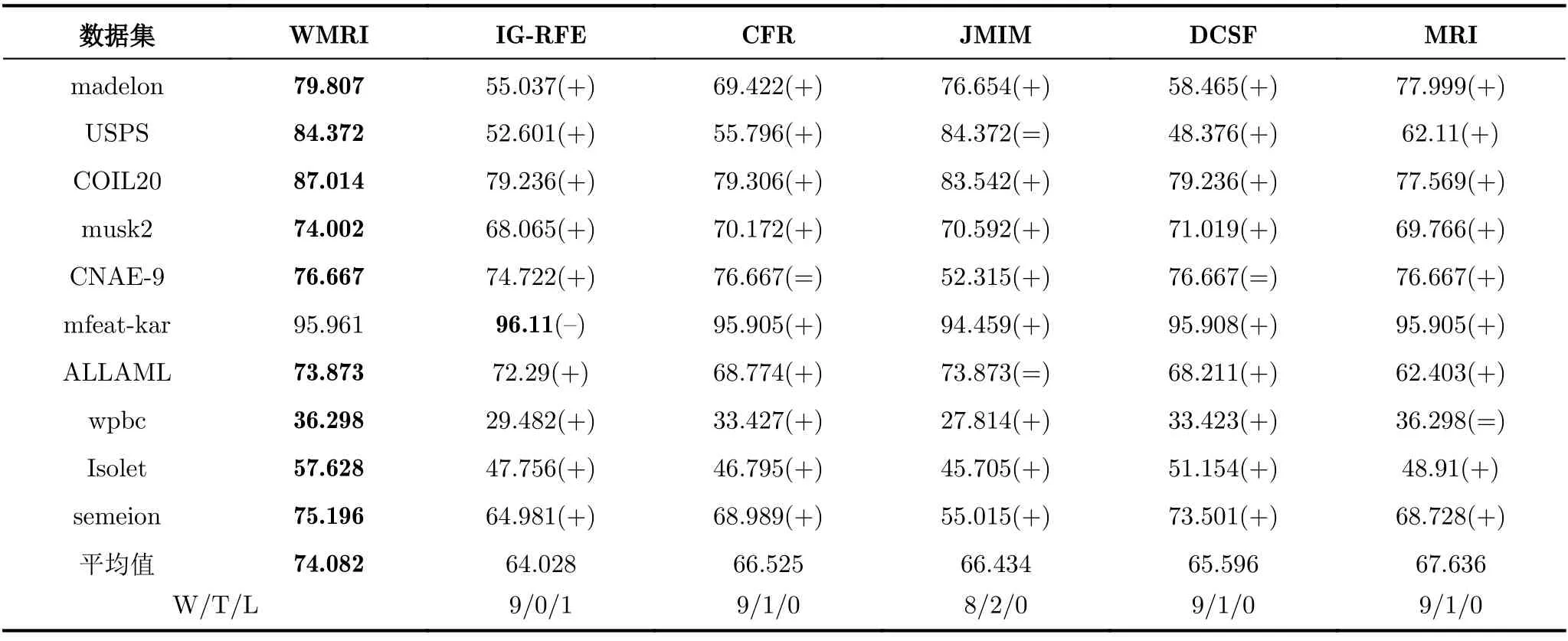
表3 KNN分類器的平均分類準確率fmi(%)

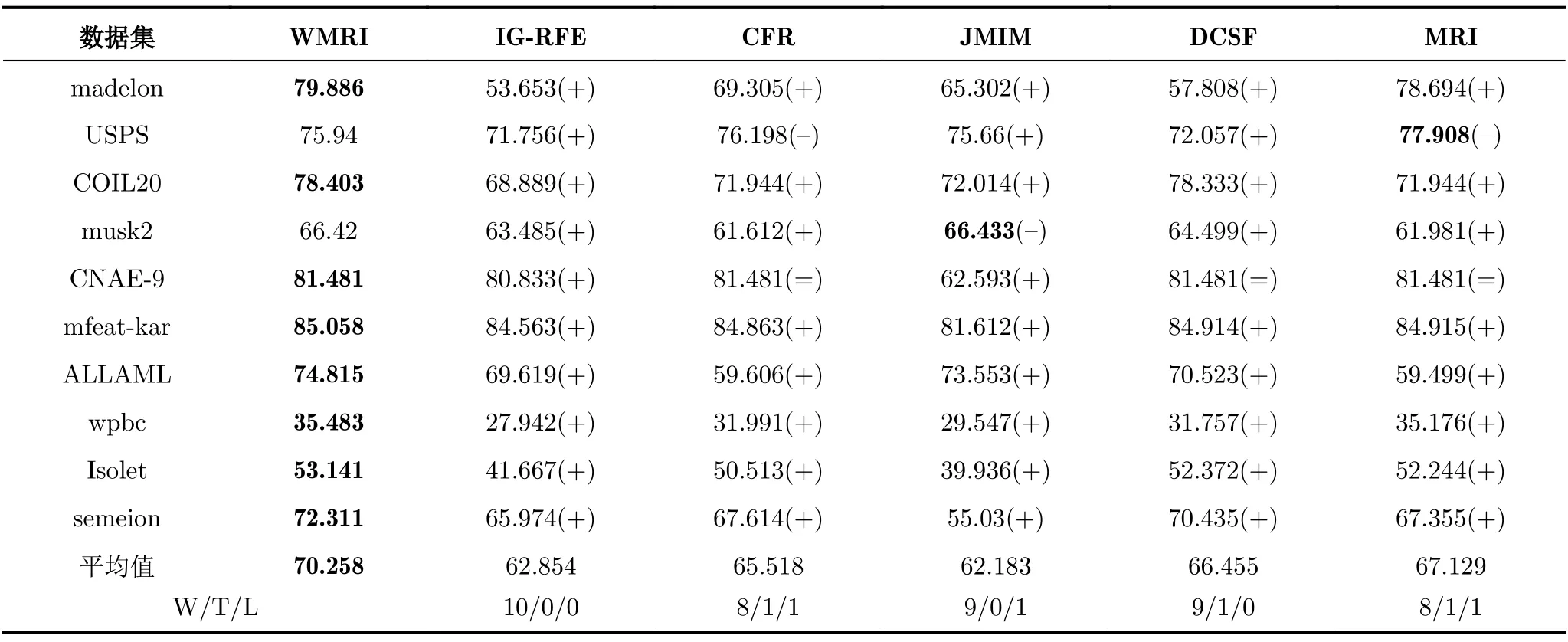
表4 C4.5分類器的平均分類準確率fmi(%)

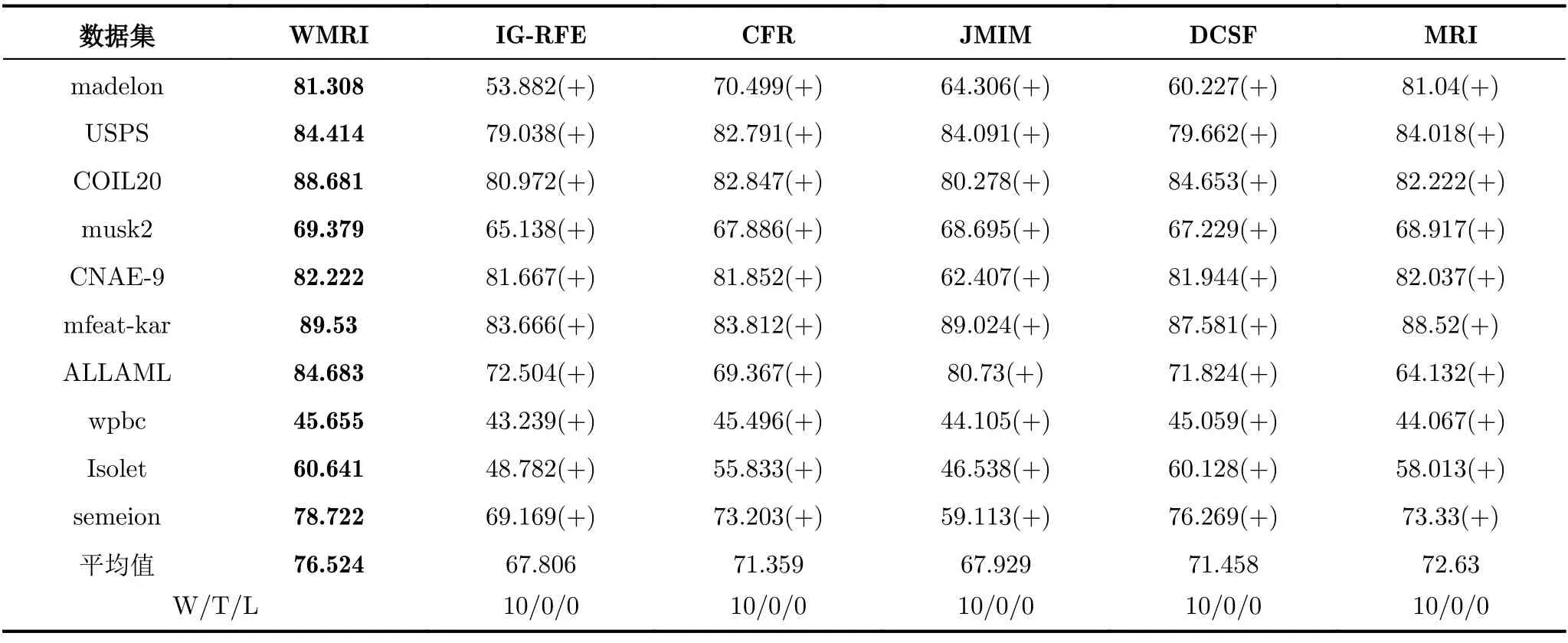
表5 Random Forest分類器的平均分類準確率fmi(%)

從表3可以得出，WMRI算法在10個數據集的平均fmi值是最高(74.082%)。同時，WMRI分別優IG-RFE,CFR,JMIM,DCSF和MRI為9,9,8,9和9次。在表4中，WMRI算法在10個數據集的平均fmi值也是最高(70.258%)。同時，WMRI分別優IG-RFE,CFR,JMIM,DCSF和MRI為10,8,9,9和8次。在表5中，WMRI算法在10個數據集的平均fmi值也是最高(76.524%)。同時，WMRI分別優IG-RFE,CFR,JMIM,DCSF和MRI為10,10,10,10和10次。

通過對表3—表5分析可以得出，不同分類器表現出的分類結果也不相同。但是，WMRI算法的平均fmi值都是最高。這說明WMRI算法優于其他特征選擇算法(IG-RFE,CFR,JMIM,DCSF和MRI)。

為了進一步觀察特征子集對fmi值的影響，圖1，圖2和圖3分別給出部分不同數據集的fmi性能比較。從圖1、圖2和圖3可以看出，當數據的維數不斷增加時，由于WMRI算法通過平均值和標準差動態調整新分類信息項I(C;fk|fsel)與保留類別信息項I(C;fsel|fk)的重要程度。結果顯示，WMRI算法明顯優于MRI算法。例如在圖1(b)和圖2(b)中，JMIM算法優于MRI算法，而WMRI算法優于JMIM算法。圖3(a)和圖3(b)，DCSF算法優于MRI算法，而WMRI算法優于DCSF算法。這些充分說明WMRI算法對分類效果的提升非常明顯。并且，WMRI明顯優于IG-RFE,CFR,JMIM,DCSF和MRI。

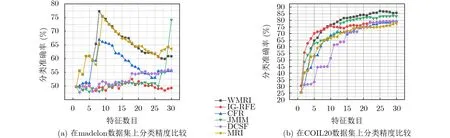
圖1 KNN在高維數據集上的性能比較

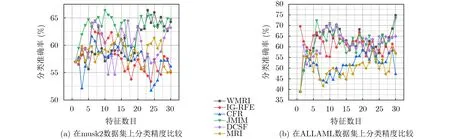
圖2 C4.5在高維數據集上的性能比較

圖3 Random Forest在高維數據集上的性能比較

4 結束語

本文提出一種基于過濾式的特征選擇方法：動態加權的最大相關和最大獨立分類特征選擇算法(WMRI)。該算法旨在解決新分類信息和保留類別信息不同重要度的問題并提高特征子集的數據質量。為了全面驗證WMRI算法的有效性，實驗在10個數據集上進行。通過使用分類器(KNN,C4.5和Random Forest)和分類準確率指標(fmi)全面評估所選特征子集的質量。實驗結果證明WMRI明顯優于MRI,CFR,JMIM,DCSF和IG-RFE等5種特征選擇算法，但WMRI算法有時也會導致特征選擇的結果不理想。未來的工作包括進一步改進新分類信息項和保留類別信息項的動態平衡問題并優化WMRI算法，同時在更廣泛的領域中驗證所提出的方法。