連續時間下政企共同運作基建的博弈分析

中國農業銀行福建省分行 余潤堃

一、研究背景

PPP是近年來我國新興的基礎設施建設模式，該項目的特點是政府與企業通力合作，通過資源互補實現共同提供公共產品。該運作模式的主要優勢在于政府的資金短缺問題可以得到有效解決，極大地減輕地方政府的財政壓力。但是，政企共同運作基建時也存在資源浪費、偷工減料引發的巨大損失，最終都需要社會公眾為損失買單。

在研究政企共同運作基建時，國外學者一致認為，政府在共同運作中要扮演好管理者的角色，盡到公共管理人的職責。薩瓦斯認為，PPP項目是政府通過合同承包、特許經營與補助等形式與企業共同參與公共服務的生產與安排過程。Samii認為PPP是政府和企業為實現可持續利益輸出的創新型合作伙伴關系。Spielman 和 Von Grebmer指 出，PPP項目是政府與企業通過優勢互補的手段，應用特定技術協同提供公共產品或服務以達到特定目標的一種合作制度。Ahmed認為，在PPP項目的實際分工當中，政府扮演維護公共利益并對企業進行監管的角色，企業負責提供公共產品與服務。Sabry的研究結果表明，PPP項目的績效提高依賴于政府辦事效率及監管水平的提高，在這種情況下，企業的投資水平也會隨之增長。

二、模型假設

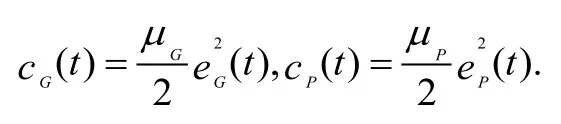
其中，μG和μP分別表示政府和企業在維護社會公眾福利過程中付出成本的系數。在現實背景下，政府與企業的成本不為負數，故μG和μP的取值范圍是(0,+∞)，則函數cG(t)和cP(t)都是關于各自努力水平的凸函數。

本文探討的政府與企業的合作基礎是社會公眾福利W，其原因在于政府代表公眾利益，其參與共同運作的出發點必然是社會福利，企業在參與共同運作時必須適當考慮社會公眾福利，完全忽視社會福利將導致共同運作的失敗[2]。故設變量W(t)∈(0,+∞)代表社會公眾福利，采用隨機微分方程刻畫公眾福利W(t)隨時間變化的趨勢：

上述福利函數中，Gλ和Pλ分別表示政府和企業的努力水平對社會公眾福利的貢獻程度，Gλ和Pλ的取值范圍是(-∞,+∞)。δ表示社會公眾福利的衰減程度，其取值范圍是(0,+∞)。在應用隨機微分方程刻畫公眾福利變化趨勢時，本文出于共同運作的實際情形，重點探討政府與企業對社會福利的增益水平。考慮到實際政企的基建合作是以招投標的形式進行，且對企業的準入門檻要求較高，則資源過度競爭導致的社會公眾福利衰減不適用本文所討論的情景，因此將社會福利的損失一般歸責于企業的不作為或者是投機行為。

假定πG(t)表示政府在t時刻的收益，πP(t)表示企業在t時刻的收益，π(t)表示政府與企業在t時刻創造的社會總收益：

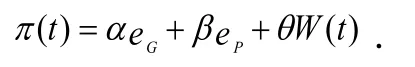
在上述函數中，α,,βθ均為大于0的常數，它們分別代表政府努力水平、企業努力水平、社會公眾福利增益對整個PPP項目運營收益的影響水平。本文模型中的收益函數π(t)由eG、eP、W(t)三部分構成，是參考文獻模型的演化。

TπG(t)表示政府在全部時間內的收益，TπP(t)表示企業在全部時間內的收益,PPP項目運營績效在政府與企業之間分配，政府預先約定的分配比例為σ,其取值范圍是(0,1)，則企業的分配比例為1-σ。η是控制變量，用來描述政府對企業的激勵，其取值范圍是(0,1)。政府與企業的貼現率r相同且為正。雙方的意圖都是在未來的無限時間內尋找使得自身利益實現最大化的最優努力策略，可將政府在無限時間內收益的目標函數表示為:

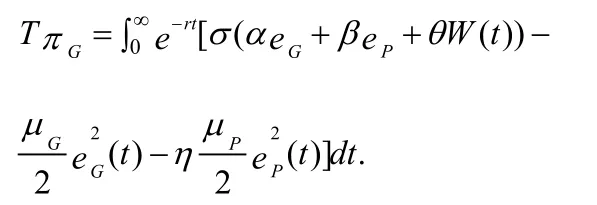
企業在無限時間內收益的目標函數表示為：

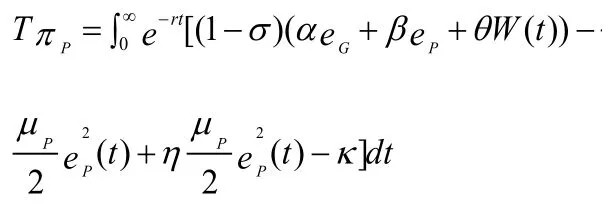
κ表示企業從金融機構拆借資金的成本，是結合本文背景考慮到企業在實際運作中可能出現的資金運作困難向金融機構拆借資金的情形，為本文對參考文獻模型的改進。

在現行的政企共同運作基建的合作中，通常呈現以政府為主導的共同運作機制，政府一般在與企業的合作中扮演領導者的角色，企業也通常會根據政府的行動采取下一步策略。本文研究政府與企業由于地位不對等帶來的決策次序不對等的情形，通過建立斯塔克爾伯格模型求解政府作為領導者情形下的雙方最優努力水平與最佳收益。在得出最優努力水平與收益后進行算例仿真分析。

三、最優收益

子博弈是指在動態博弈中，所有參與人先后采取了一次行動后所構成的一組新的博弈，這組博弈中的每個策略組合都稱為“子博弈”。當參與人在子博弈系列中的每一個子博弈都構成納什均衡時，該情形稱作子博弈精煉納什均衡。在政府與企業的共同運作中，當政府采取對抗或是協作的策略時，企業會根據政府的行為作出相應的策略反應，此時雙方的策略組合構成子博弈。為使每個子博弈都達成納什均衡，需要進行策略的倒推演算。

政府將首先選擇自有的努力付出水平及對企業的激勵因子，企業在觀察到政府的行為并且接收到其釋放的訊號后，選擇有利于自身的行為決策及資本結構。雙方的博弈過程完全符合主從博弈的邏輯及過程。政府是博弈行為的領導者，企業是博弈行為的跟隨者。為了得出斯塔克爾伯格模型的均衡結果，需要運用逆向分析法求解。

政府與企業的收益是關于時間的函數，且該函數與社會公眾福利變量W(t)相關無法直接求解，結合參考文獻用動態規劃原理構造優化問題進行求解。

企業的連續有界微分最優收益函數對所有的W≥0滿足優化問題：

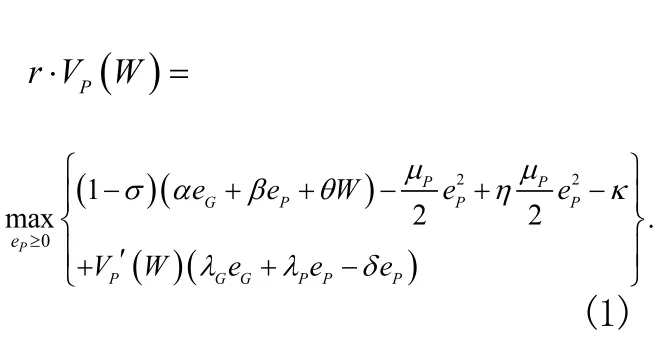
政府的連續有界微分最優收益函數對所有的W≥0滿足優化問題：

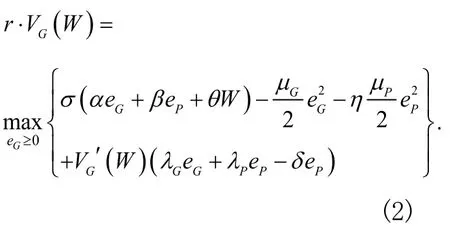
首先求解企業的最佳收益，對上述等式的右端部分求其對eP的一階偏導數并令其為0，得如下結果：

得到政府和企業最優收益函數，分別對W求導后得到的導數代入即可得政府和企業最優努力水平、政府最優激勵系數如下：

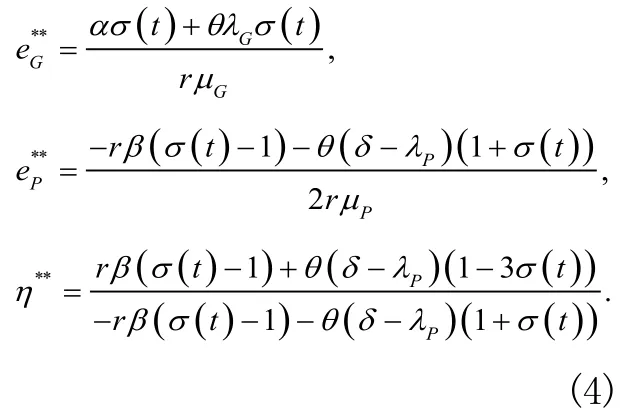
在實際的政企合作中，企業的收益顯著受到政府對其好感程度的制約，同時也受到政府所關心的社會公眾福利的制約。

四、數值仿真

以政府收益分配比例為自變量，最優收益為因變量，其他參數取定值作比較分析圖。可設定時間t=1，衰減率δ=0.1，貼現率r=0.1，激勵系數η=0.2，政府與企業付出的成本系數μG=1,μP=2，政府與企業的努力對社會公眾福利的影響系數λG=1,λP=2，企業從金融機構拆借資金的成本κ=0.05，政企在時刻t=1組成的總收益系數θ=1,α=2,β=3。由上述參數設定值可以得到政企同時行動下政府最優收益、企業最優收益、社會最優收益關于政府收益分配比例的函數圖像（見圖1），其中σ∈(0,1)。

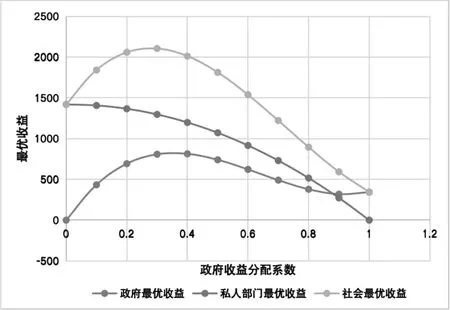
圖1 最優收益關于政府收益分配比例函數圖

以時間t為自變量，最優收益為因變量，其他參數取定值作比較分析圖。可設定分配比例σ=0.4，衰減率δ=0.1，貼現率r=0.1，激勵系數η=0.2，政府與企業付出的成本系數μG=1,μP=2，政府與企業的努力對社會公眾福利的影響系數λG=1,λP=2，企業從金融機構拆借資金的成本κ=0.05，政企在t時刻組成的總收益系數θ=1,α=2,β=3。由上述參數設定值可以得到政企同時行動下政府最優收益、企業最優收益、社會最優收益關于時間t的函數（見圖2），其中t∈(0,+∞)。

圖2 最優收益關于時間函數圖

五、管理啟示

在主從博弈初期，政府的收益分配系數的高低與否對社會總體收益的增減幾乎不產生影響，政府需要注意制定合理的收益分配系數，協調自身與企業的利益，使收益分配在遵循公平原則的同時能滿足雙方的需求。在項目長期運營的情況下，政府主導項目控制權的優勢將顯著顯現出來，提示政府在實務中積極參與項目規則的制定，主動引導企業遵循規則并維護公眾福利。企業在主從博弈下盡管在項目初期受到政府的管制較多，但從長期來看，與政府的關系將逐漸緩和，在長期共同運作下，企業要注意在遵守規則的同時適當發揮主觀能動性，以創造更大的項目價值。