基坑吊腳墻支護中鎖腳錨索的設計方法探討
陳富強,楊光華, ,周沛棟,李支令,喬國龍
(1.廣東省水利水電科學研究院,廣州 510635; 2.廣東省巖土工程技術研究中心,廣州 510635;3. 華南理工大學土木與交通學院,廣州 510640;4.廣東省水利電力勘測設計研究院有限公司,廣州 510635;5.廣東粵海珠三角供水有限公司,廣州 511458)
1 概述
一般情況下,基坑工程中的擋土結構(地連墻或樁)的嵌固深度需要滿足整體穩定性驗算、抗隆起驗算、抗傾覆(踢腳破壞)穩定性驗算和嵌固段基坑內側土反力驗算的要求,當坑底以下為軟土時,其嵌固深度還需要滿足繞最下層支點為軸心的圓弧滑動穩定性的要求。然而,當遇到上覆土層,下部巖層埋藏淺且強度很高的土巖組合地質條件,或者當基坑開挖很深,基坑底面已處于中風化甚至微風化的硬巖層中時,在基坑支護設計時,綜合考慮到支護的經濟性、工期和施工的難度等因素,通常采用“吊腳墻(樁)”支護。廣東省地質條件多樣性,決定了某深基坑工程支護形式的多樣性,各種支護形式都在應用[1],其中吊腳式支護結構在高層建筑(如廣州東塔)、城市地鐵(如廣州地鐵、東莞地鐵)等的基坑工程中廣泛應用[2-10],但是其設計計算理論卻還不成熟,國家和地方的基坑規范規程尚未有相關的設計條文。吊腳式支護的通常做法,為了保證“吊腳墻(樁)”墻(樁)腳的安全,在墻(樁)入巖面以下預留一定寬度的巖肩固定墻(樁)腳。但由于施工爆破等方面的影響,預留巖肩可能會被破壞,損失了對墻(樁)腳的支撐作用,此時,為了防止腳根不穩,導致造成墻底塌方,產生危險,往往會在吊腳墻(樁)底增加鎖腳錨索來固住墻(樁)腳,可見,鎖腳錨索的設計在吊腳墻(樁)支護設計中是至關重要的。李棟[11]等采用強度折減法研究了吊腳支護,指出護樁彎矩隨工況的變化趨勢,表明在基巖垂直開挖后,需重點關注鎖腳錨桿軸力和預留巖肩的完整程度對二元巖土基坑穩定性的控制作用。
在吊腳墻(樁)設計計算的研究方面,劉建偉[12]根據吊腳樁支護體系受力原理和分步開挖工況,提出系統的“吊腳樁”支護體系計算模型,上部樁錨結構按“零嵌固”排樁模型計算,鎖腳錨索通過抗踢腳穩定性計算其承載力,下部巖層基坑分別按復合土釘墻模型進行圓弧穩定性驗算和巖質邊坡模型進行平面穩定性驗算。徐濤[13]等介紹了吊腳樁在廣州地鐵中的應用,將“吊腳樁”組合圍護體系分成兩部分,分別采用彈性增量法計算分析。從已有資料來看,若鎖腳錨索的設計拉力通過極限平衡分析(如抗踢腳穩定)確定尚不合理,因為未考慮施工過程的影響,若以巖肩頂面處作為分界線,按“零嵌固”彈性支點法計算錨索拉力,則可能導致計算的錨索拉力偏小。因此,為了保證吊腳式支護結構的安全穩定,進一步完善鎖腳錨索的設計方法是非常必要的。為此,本文對吊腳墻支護中鎖腳錨索的設計方法進行了研究,提出了符合施工過程的設計計算方法,可供設計人員參考使用。
2 鎖腳錨索設計計算原理
根據增量法的計算原理,在多支撐支護結構中,支撐或錨桿都是先開挖后支撐的,即支撐前結構已變形,且不同過程中其計算的力學體系也是不同的,為此,對多支撐的支護結構的受力,采用增量法進行計算才符合實際[14-15]。
為了分析方便起見,以圖1的吊腳式支護體系為例,說明鎖腳錨索的設計計算原理。與通常的做法一樣,將吊腳式支護體系分成上、下兩部分進行分析計算,為了分析鎖腳錨索拉力的計算,取上部結構進行分析,計算模型如圖2所示,即取巖肩頂面處的標高作為基坑的底面標高,支護墻(樁)按實際長度,計算模型中不加鎖腳錨索,根據施工過程,用增量法計算至基坑底面,采用等效替代思想,此時基坑開挖面以下,巖層對支護墻(樁)坑底以下的抗力之和即為鎖腳錨索需要提供的水平向拉力之和,可以理解為后期由于巖肩內側的開挖,原本由巖肩對支護墻(樁)提供的抗力轉移至了鎖腳錨索,即力的轉移,不考慮巖肩對支護墻(樁)的有利作用,將其作為安全儲備考慮,設計計算的鎖腳錨索的拉力是偏大的,故設計方案是偏安全,因此,采用此方法計算,可以避免判斷按極限平衡分析確定的錨索拉力是否安全可靠的問題,避開了采用極限分析方法的缺點,且設計計算的錨索拉力是考慮了施工過程影響的,更符合基坑的受力和變形實際。
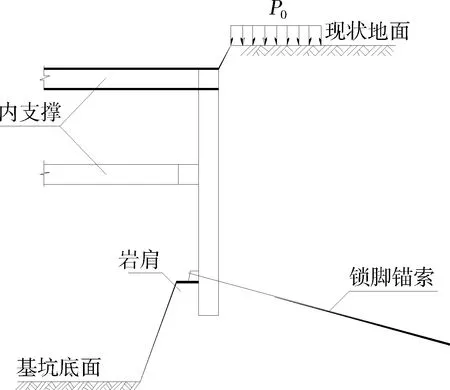
圖1 吊腳式支護結構示意
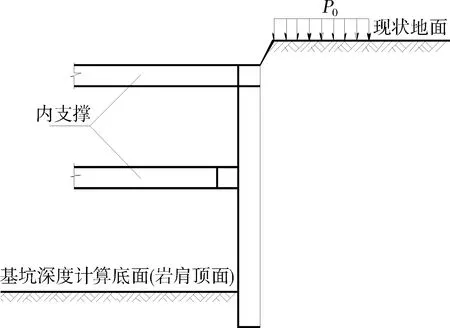
圖2 吊腳式支護結構(上部結構)示意
可見,由水平方向的靜力平衡條件,作用在擋土構件嵌固段上的基坑內側土反力合力=錨索的水平分向的合力,然后根據錨索的傾角,可以求得軸力計算值(見圖3):
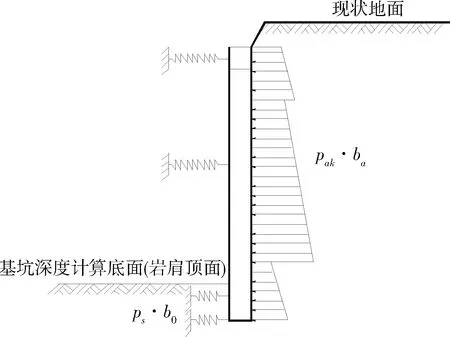
圖3 吊腳式支護結構簡化計算模型示意
T=∑Psb0
(1)
式中:
T——錨索的水平分向的合力,kN;
Ps——作用在擋土構件嵌固段上的基坑內側的分布土反力,kPa;
b0——擋土結構的土反力計算寬度,m。
3 案例分析
以珠江三角洲水資源配置工程SL01#盾構工作井基坑支護為例。SL01#工作井外徑為34.3 m圓形豎井,地面平整高程為44.0 m,基坑底高程為-4.88 m,開挖深度為48.88 m。采用地下連續墻+砼內襯墻及錨桿支護方案,地連墻墻厚為1 m,土層襯砌后內徑為29.9 m,巖層襯砌后內徑為26.8 m。上部采用地下連續墻和逆作法鋼筋砼內襯墻支護,下部弱風化變質巖段井身采用預應力錨桿和逆作法鋼筋砼內襯墻支護。其具體的基坑支護結構設計為:上部連續墻采用吊腳式,墻厚為 1.0 m,墻底嵌入弱風化巖不小于3.5 m,底部采用兩層預應力錨索鎖腳,錨索(5Φs15.2)單根長L=11 m,傾角為15°,布置間距為2.0 m×2.0 m;下部弱風化巖段錨桿(1Φ25)單根長L=6 m,傾角為15°,布置間距為1.5 m×1.2 m,并采用掛鋼筋網噴砼(厚度250 mm)護面,平面和剖面示意如圖4和圖5所示。
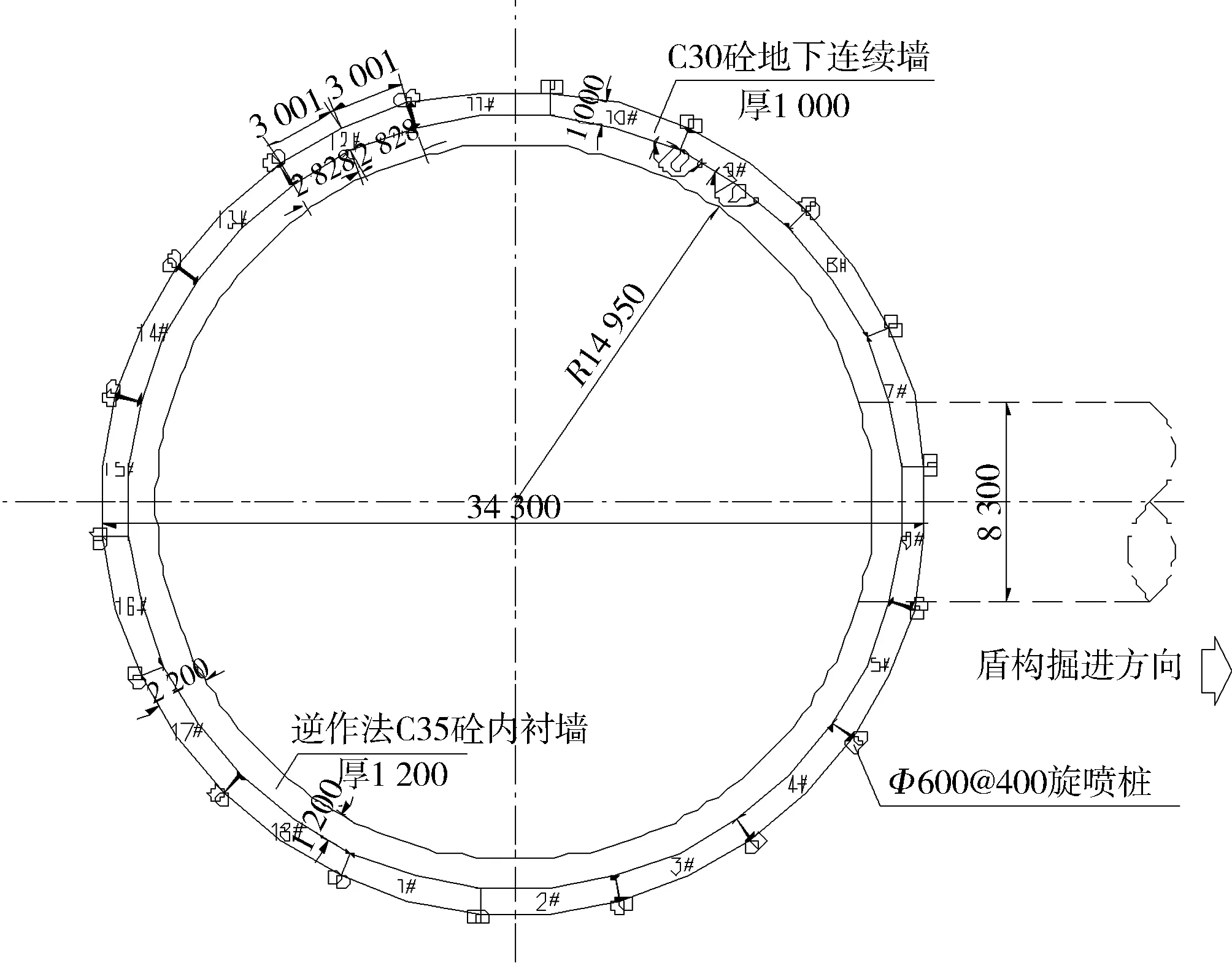
圖4 SL01#工作井平面示意(單位:mm)
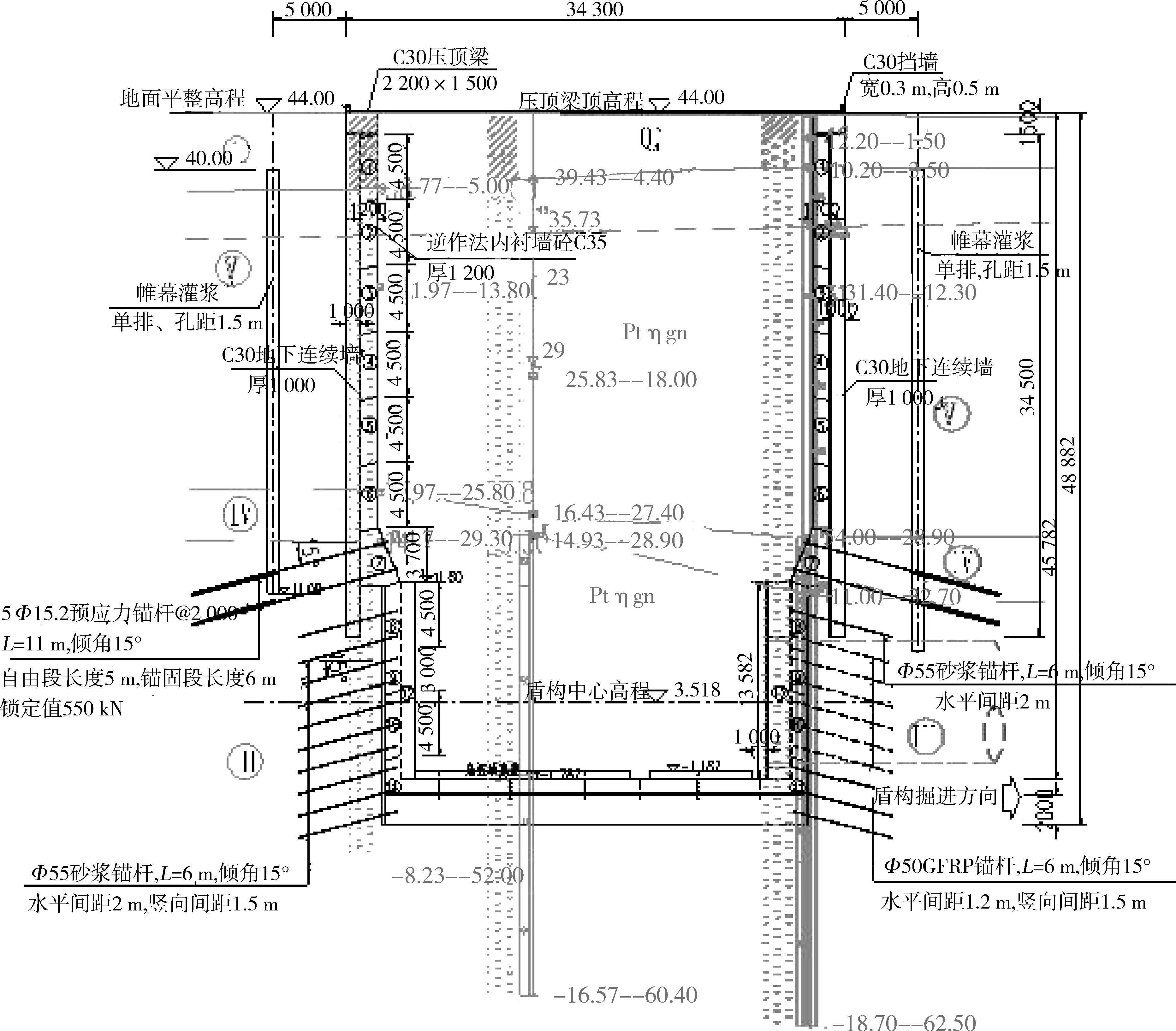
圖5 SL01#工作井剖面示意(單位:尺寸mm,高程m)
基坑圍護結構側壁安全等級為1級,結構重要性系數為 1.1。始發井基坑周邊施工超載按35 kPa控制,盾構機吊裝布置于端頭洞門側,地面超載按70 kPa考慮;根據鉆孔揭露,巖土層依次為人工填土,松散狀填土,壓縮性高,自穩能力差;坡積土,由泥質砂礫等組成,透水性較大,雜亂,壓縮性高,易沖刷破壞;全風化變質巖,呈砂礫質粉質黏土狀,黏粒含量低,韌性較差,干強度一般;強風化變質巖,強風化巖風化劇烈,巖體呈碎裂結構,夾有全風化夾層,整體穩定性差;弱風化變質巖,弱風化巖體為塊狀~整體狀結構,巖質堅硬,完整性好。各層土的物理力學參數建議值見表1。
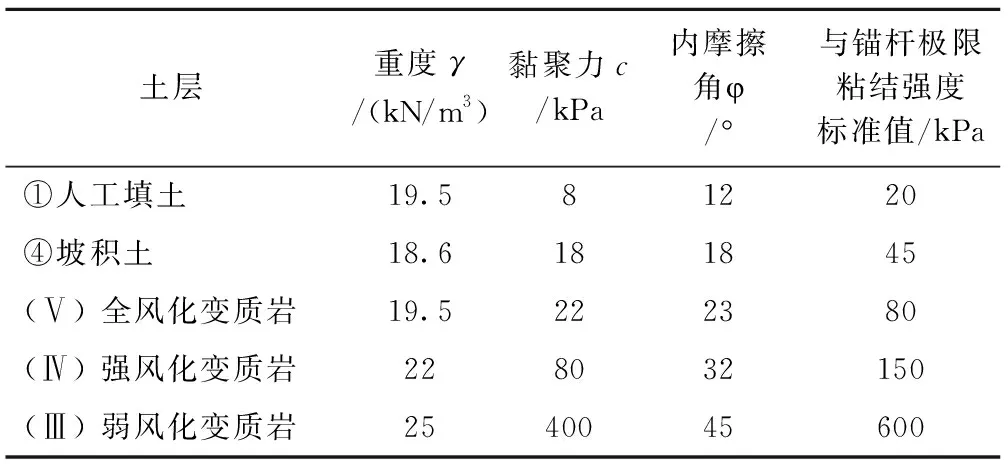
表1 各土層物理力學參數建議值
根據《港口工程地下連續墻結構設計與施工規程》(JTJ 303—2003)中圓形支護地下連續墻結構設計的有關規定。圓形支護地下連續墻結構宜按空間結構計算,也可按軸對稱結構取單位寬度的墻體作為豎向彈性地基梁計算。墻體和環梁的環向效應,可按軸對稱結構簡化為等效彈性支撐。
當圓形支護地下連續墻結構利用環梁作支撐時,可將環梁的作用以等效支撐彈簧來替代(如圖6所示)。單位寬度墻體上環梁的等效彈性支撐系數可按式(2)計算:
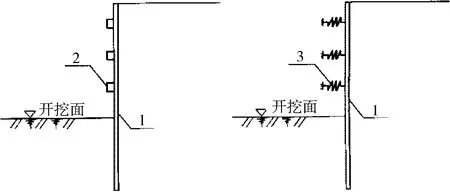
a 環梁支撐 b 等效支撐彈簧
(2)
式中:
Kh——環梁的等效彈性支撐系數,kN/m2;
Eh——環梁材料的彈性模量,kN/m2;
Ah——環梁截面面積,m2;
Rh0——環梁中心線初始半徑,m。
圓形支護墻體的環向效應可采用分布的支撐彈簧來替代(如圖7所示)。單位寬度地下連續墻墻體的等效分布彈性支撐系數可按式(3)計算:
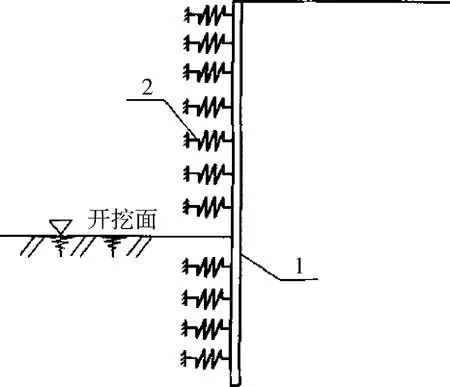
1-地下連續墻墻體;2-等效分布支撐彈簧
(3)
式中:
Kd——墻體的等效分布彈性支撐系數,kN/m3;
Ed——地下連續墻環向綜合壓縮模量,kN/m2,Ed=αE,E為地下連續墻混凝土彈性模量,kN/m2,α=0.5~0.7,本次分析中取α=0.5,當R0較大,或槽段數較多時取小值;
b——地下連續墻的墻體厚度,m;
R0——墻體中心線半徑,m。
采用北京理正深基坑軟件增量法計算,計算深度取32.5 m,即鎖腳錨索所在的內襯墻底面,嵌固深度為3.5 m,計算結果如圖8所示。
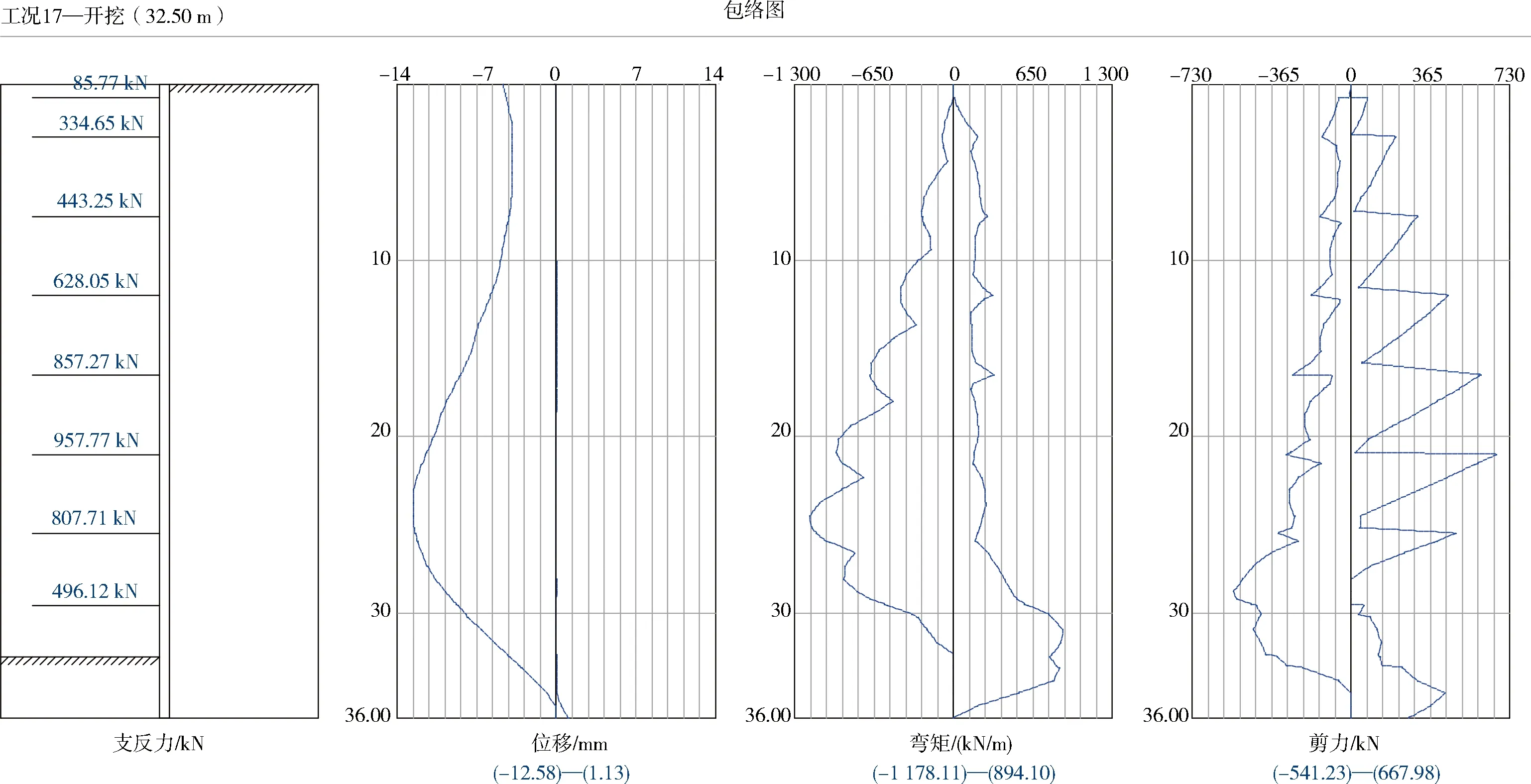
圖8 增量法計算結果示意
計算至開挖底時,作用在擋土構件嵌固段上的基坑內側土反力合力∑Psb0=529 kN/m(如圖9所示),設計了兩排錨索,錨索(5Φs15.2)單根長L=11 m,傾角為15°,水平間距為2 m,根據前面的鎖腳錨索的計算方法,則每根錨索的軸力T=529 kN/m×2 m÷2根÷cos15°=548 kN,根據施工圖,設計的錨索鎖定值為550 kN。由于現場沒有布置鎖腳錨索的拉力監測,但從現場測斜監測數據來看,實測的最大水平位移為8.68 mm(如圖10所示),小于計算的最大位移為12.58 mm,可見,錨索的設計還是合理、可靠的。
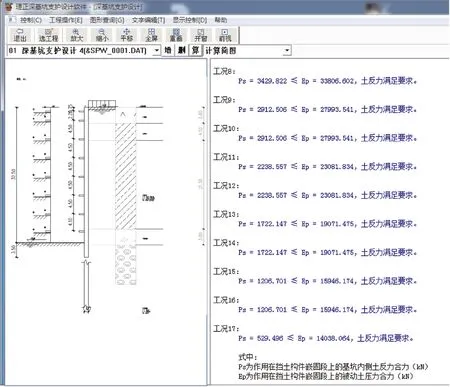
圖9 各工況下基坑內側土反力合力計算結果示意
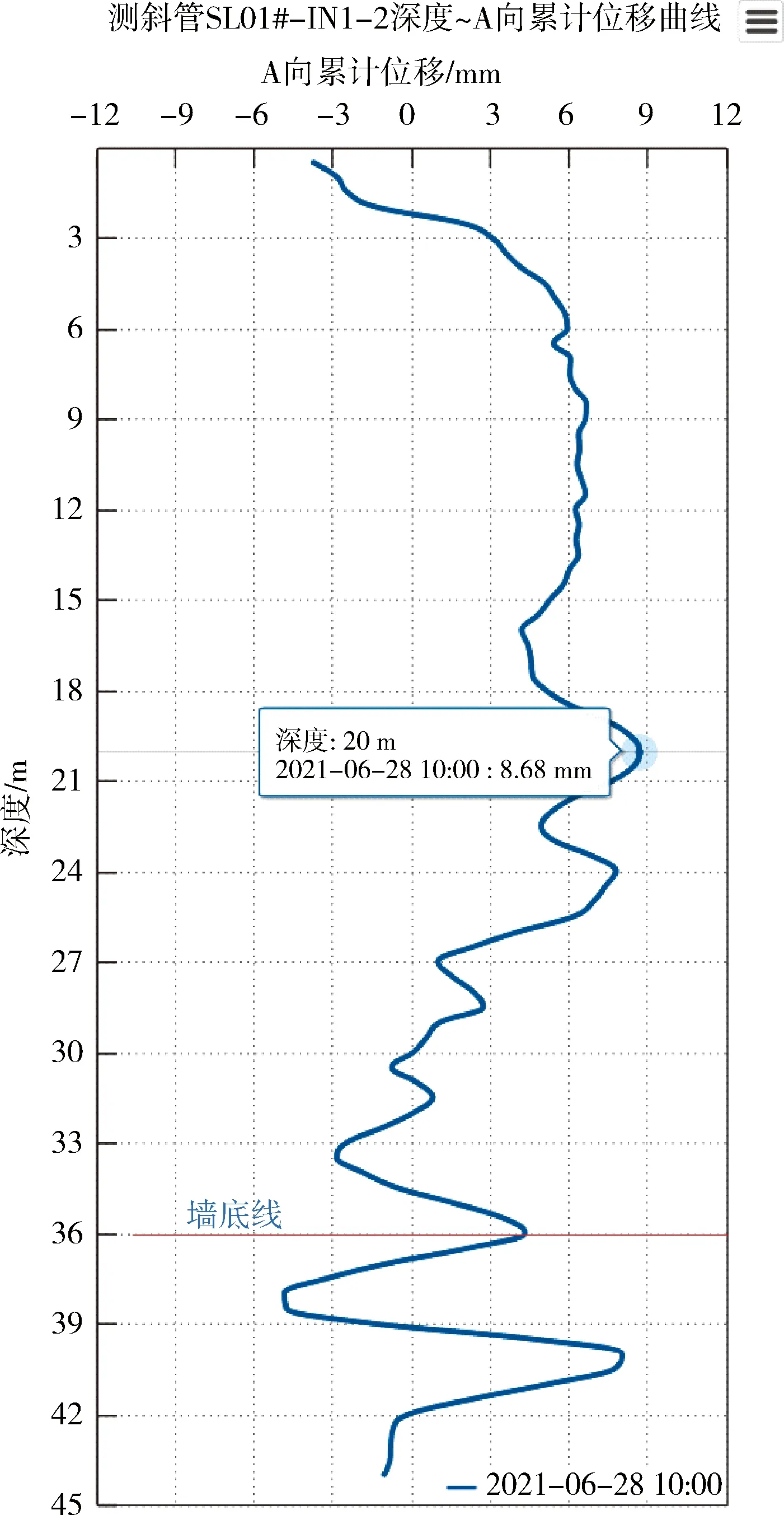
圖10 現場監測測斜累計位移示意
3 結語
針對目前吊腳式支護中鎖腳錨索拉力設計方法尚缺少有效計算方法的現實問題,本文從吊腳式支護結構受力的實際出發,分析了鎖腳錨索的受力過程,從力的轉移的角度,提出了將坑底以下基坑內側土反力合力等效為鎖腳錨索的水平拉力之和,并以一個實際工程的鎖腳錨索設計為例,分析了計算過程,通過監測數據對比,初步驗證了方法的可行性。本文提出的鎖腳錨索的計算方法是考慮了施工過程影響,由此計算的基坑支護的受力和變形更符合工程實際,是一種比較可靠的計算方法,可供類似工程設計參考。

