二輪自平衡機器人系統(tǒng)設(shè)計
彭小丹 劉金溢

DOI:10.19850/j.cnki.2096-4706.2021.09.037
摘? 要:二輪自平衡移動機器人在狹小空間中具有較高的適用性,是一種典型的欠驅(qū)動系統(tǒng)。文章研究了二輪自平衡機器人的動力學(xué)建模方法,完成了控制系統(tǒng)設(shè)計,基于Simulink實現(xiàn)了二輪自平衡機器人仿真和控制程序一體化設(shè)計,縮短了開發(fā)周期。設(shè)計了以STM32單片機為核心的二輪自平衡機器人控制器,基于Simulink編程方式實現(xiàn)了機器人的直立和行進控制。經(jīng)仿真和實際測試表明,該二輪自平衡機器人能夠較好地控制車體保持平衡狀態(tài),具有較強的穩(wěn)定性。
關(guān)鍵詞:Simulink;PID控制;二輪自平衡機器人;STM32
中圖分類號:TP242.6;TP273 文獻標(biāo)識碼:A 文章編號:2096-4706(2021)09-0141-04
The System Design of Two-Wheeled Self-Balancing Robot
PENG Xiaodan,LIU Jinyi
(North China University of Technology,Beijing? 100144,China)
Abstract:Two-wheeled self-balancing robot has a high applicability in a confined space,which is a typical underactuated system. This paper researched the method of dynamic modelling for the two-wheeled self-balancing robot and finished the design of control system. Based on Simulink,the integrated design of simulation and control program of two-wheeled self-balancing robot is realized,which shortens the development cycle. A two-wheeled self-balancing robot controller based on STM32 single chip microcomputer is designed. The vertical and moving control of the robot is realized based on Simulink programming. The simulation and actual test show that the two-wheeled self-balancing robot can better control the vehicle body to maintain the balance state and has strong stability.
Keywords:Simulink;PID control;two-wheeled self-balancing robot;STM32
0? 引? 言
二輪自平衡移動機器人具有體積小、靈活度高、可應(yīng)用于狹小作業(yè)空間的優(yōu)點。二輪自平衡機器人系統(tǒng)是一個高階次、不穩(wěn)定、多變量、非線性、強耦合的系統(tǒng)[1]。該類機器人的控制器開發(fā)通常先完成理論仿真驗證控制系統(tǒng)設(shè)計的可行性再開發(fā)實際控制器,開發(fā)過程耗費時間較長。而基于模型設(shè)計的方法可實現(xiàn)仿真與實際控制器一體化開發(fā),能夠提高開發(fā)效率。
作為控制理論算法實踐平臺之一的二輪自平衡機器人,眾學(xué)者對其系統(tǒng)設(shè)計展開了大量研究。史策通過MATLAB對模糊滑模控制器和卡爾曼濾波器進行仿真,利用Keil5集成開發(fā)環(huán)境完成編寫程序代碼和調(diào)試工作[2]。朱年華對二輪自平衡機器人建立動力學(xué)模型,并通過MATLAB設(shè)計控制算法進行仿真,在KEIL平臺下實現(xiàn)程序設(shè)計[3]。錢慶文通過調(diào)動動態(tài)鏈接庫,采用MATLAB和VC++混合編程的方式實現(xiàn)對機器人的控制,降低了開發(fā)成本[4]。目前現(xiàn)有開發(fā)方式多數(shù)通過MATLAB平臺進行算法仿真,利用KEIL集成開發(fā)環(huán)境編寫程序代碼的方式分步開發(fā),多平臺多次編程的開發(fā)方式開發(fā)周期較長。
本系統(tǒng)設(shè)計利用模型化開發(fā)方式,基于Simulink軟件平臺的快速控制原型方法,采用將建模、仿真與實際代碼編寫一體化的開發(fā)方式,提高開發(fā)效率。本系統(tǒng)設(shè)計以STM32F4系列微處理器為控制核心,采用HI229姿態(tài)測量傳感器,通過PID控制算法實現(xiàn)平衡車的直立和行走。Simulink軟件設(shè)計開發(fā)平臺通過模塊化的方式搭建控制算法,具有可視性高,易于模塊化管理的特點。經(jīng)仿真和實例驗證,本文設(shè)計的系統(tǒng)具有較高的可行性和實用性。
1? 理論模型及仿真
1.1? 動力學(xué)建模
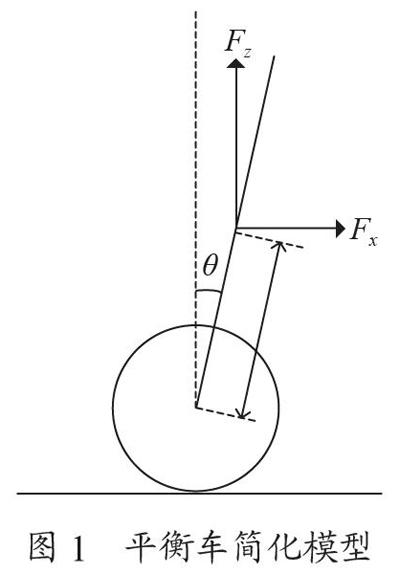
二輪自平衡機器人通過電機轉(zhuǎn)矩改變車體運動姿態(tài),當(dāng)機器人車體發(fā)生傾斜時,電機驅(qū)動車輪產(chǎn)生與車體傾斜方向相同的加速度進行補償,以達到保持平衡的目的。由于二輪自平衡機器人系統(tǒng)控制輸入為電機扭矩,因此二輪自平衡機器人系統(tǒng)是一個非線性系統(tǒng),其數(shù)學(xué)模型較為復(fù)雜。結(jié)合實際與理論推導(dǎo)需求,本文假設(shè)該二輪自平衡機器人系統(tǒng)結(jié)構(gòu)對稱,左右輪參數(shù)相同,從而可將系統(tǒng)簡化為如圖1所示的模型[5]。
圖1中,θ表示車體與垂直方向的偏角,l表示車體質(zhì)心到車輪軸的距離,mt和mw分別為車體和車輪質(zhì)量。將二輪自平衡機器人分解成車體和車輪兩部分分別采用牛頓力學(xué)分析法對系統(tǒng)進行分析,從而推導(dǎo)出系統(tǒng)輸入量電機扭矩與輸出量二輪自平衡機器人車體偏角和整體速度之間的關(guān)系。
車體在水平方向的位移xd可表示為車輪在水平方向的位移x與車體相對車輪在水平方向上位移之和:
xd=x+lsinθ
即車體在水平方向上的加速度為:
姿態(tài)發(fā)生變化,通過反饋控制實現(xiàn)系統(tǒng)閉環(huán)。
二輪自平衡機器人主要通過角度環(huán)控制保持直立穩(wěn)定狀態(tài),采用PD控制算法實現(xiàn)。當(dāng)平衡車朝某個方向倒下時,車體實際角度會與期望角度產(chǎn)生偏差,通過比例(P)環(huán)節(jié)控制減小偏差。當(dāng)比例系數(shù)Kpa較大時,系統(tǒng)會發(fā)生振蕩,通過微分(D)環(huán)節(jié)預(yù)測偏差信號的變化趨勢,降低系統(tǒng)超調(diào)。為了使二輪自平衡機器人能夠保持穩(wěn)定,還需加入速度環(huán)控制。利用積分環(huán)節(jié)消除靜差,采用PI控制算法使二輪自平衡機器人以給定速度移動。角度環(huán)控制是二輪自平衡機器人保持平衡的主要控制方法,速度環(huán)控制相對其而言屬于干擾信號,為了減小二輪自平衡機器人速度對角度環(huán)的干擾,對速度進行一階濾波,減緩速度差值。
仿真過程中,假設(shè)二輪自平衡機器人初始狀態(tài)x0=[0? 0? 0.1? 0]T,即車體初始角度為5.73°。根據(jù)圖3角度變化曲線可知,系統(tǒng)調(diào)節(jié)時間約為47 ms,超調(diào)角度為0.2°左右,系統(tǒng)超調(diào)量約為3.5%。根據(jù)仿真結(jié)果可以推測,角度環(huán)PD控制和速度環(huán)PI控制能夠使二輪自平衡機器人保持平衡,且具有較好的穩(wěn)定性、準(zhǔn)確性和快速性。
2? 控制系統(tǒng)設(shè)計
二輪自平衡機器人控制系統(tǒng)是一個閉環(huán)系統(tǒng),通過霍爾編碼器和姿態(tài)傳感器獲取車體實時姿態(tài)運動信息,將采集的數(shù)據(jù)與期望值輸入控制器進行實時控制,并作用于電機實現(xiàn)二輪自平衡機器人的運動控制。本系統(tǒng)采用GM37直流電機,該電機通過霍爾編碼器來實現(xiàn)位置信息反饋。根據(jù)AB兩相信號輸出高低電平的先后順序來確定電機的正反向運動,通過單位周期內(nèi)脈沖數(shù)量得到電機轉(zhuǎn)速。姿態(tài)傳感器通過串口通信將獲取的角速度和歐拉角等姿態(tài)信息發(fā)送給上位機。控制器具有較高的運算能力,能夠?qū)@取的外部信息進行融合處理,利用各類控制算法進行控制,通過定時器輸出通道輸出PWM控制電機,設(shè)置輸出端口高低電平實現(xiàn)電機正反轉(zhuǎn)控制,從而使二輪自平衡機器人姿態(tài)發(fā)生改變,控制系統(tǒng)結(jié)構(gòu)圖如圖4所示。
結(jié)合二輪自平衡機器人平衡狀態(tài)下各個方向上運動速度慢和角度信息反饋精確等特點,該硬件系統(tǒng)采用HI229姿態(tài)測量模塊,其集成了三軸加速度計、三軸陀螺儀和一款微控制器,可以通過串口通信的方式向上位機發(fā)送姿態(tài)信息,滿足系統(tǒng)姿態(tài)信息獲取需要。其最大幀數(shù)輸出速率為200 Hz,符合控制器每5 ms更新一次數(shù)據(jù)的要求。TB6612FNG驅(qū)動模塊可以提升單片機I/O引腳的帶載能力,可使微控制器同時控制2個直流電機。GM37電機配備正交編碼器,可以通過TB6612FNG驅(qū)動模塊直接獲取電機方向標(biāo)志位和編碼值到控制器,并根據(jù)定時器設(shè)置的數(shù)據(jù)采集頻率,解算得到電機轉(zhuǎn)速。硬件系統(tǒng)框圖如圖5所示。
3? 實例驗證
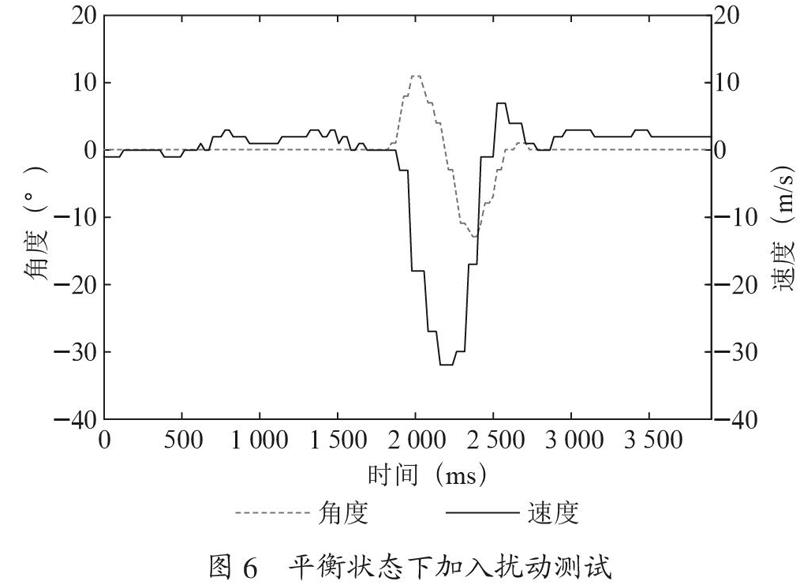
根據(jù)仿真結(jié)果的可行性,對實際系統(tǒng)進行控制,通過Simulink在仿真模型的基礎(chǔ)上實現(xiàn)I/O口、定時器、串口等功能完成實際控制系統(tǒng)模型搭建,將模型編譯生成C代碼,在Keil5下進行在線調(diào)試,實時記錄平衡車角度和速度的變化。在平衡車保持直立穩(wěn)定的狀態(tài)下,輸入一個擾動信號,觀察系統(tǒng)響應(yīng)過程和特性。二輪自平衡機器人的角度和速度變化如圖6所示,橫坐標(biāo)為時間軸(ms),縱坐標(biāo)為角度值(°)和速度值(m/s)。
如圖6所示,車體受到擾動后最大偏角為-13°,系統(tǒng)經(jīng)0.8 s左右達到穩(wěn)定狀態(tài),車體瞬時速度最高達到-32 m/s。在上電前將二輪自平衡車傾斜20°,通過觀察二輪自平衡車的角度和速度變化檢測平衡車的控制性能,如圖7所示。
上電后,車體角度迅速向當(dāng)前傾斜角度的反方向擺動,上升時間約為0.1 s,峰值時間約為0.2 s,約0.9 s后系統(tǒng)達到穩(wěn)定狀態(tài),響應(yīng)速度較快,系統(tǒng)超調(diào)量大約為25%。根據(jù)圖6、7測試結(jié)果可知,本系統(tǒng)設(shè)計具有較好的穩(wěn)定性和可行性。
4? 結(jié)? 論
本文首先對二輪自平衡機器人進行動力學(xué)分析,建立狀態(tài)空間方程,通過Simulink搭建被控對象模型以及PID控制算法,經(jīng)仿真驗證本系統(tǒng)設(shè)計可行。通過分析系統(tǒng)性能需求,本系統(tǒng)設(shè)計采用STM32F4系列微處理器為控制核心,利用HI229姿態(tài)測量傳感器獲取車體姿態(tài)信息,通過PID控制算法實現(xiàn)閉環(huán)控制。根據(jù)仿真結(jié)果的可行性,通過Simulink對實際控制系統(tǒng)進行設(shè)計,經(jīng)實際測試本系統(tǒng)設(shè)計具有較好的穩(wěn)定性和可行性。后期將以本文設(shè)計系統(tǒng)為搭載平臺,對各類控制算法進行研究。
參考文獻:
[1] 王恒,桑元俊.基于新型慣性傳感器的兩輪自平衡車的設(shè)計 [J].現(xiàn)代電子技術(shù),2017,40(18):49-54.
[2] 史策.模糊滑模控制在兩輪自平衡小車中的應(yīng)用研究 [D].馬鞍山:安徽工業(yè)大學(xué),2019.
[3] 朱年華.兩輪自平衡電動車控制系統(tǒng)設(shè)計與研究 [D].南昌:華東交通大學(xué),2016.
[4] 錢慶文.兩輪自平衡車擺機器人建模與控制方法的研究 [D].哈爾濱:哈爾濱理工大學(xué),2019.
[5] 姜立標(biāo),何家壽.兩輪自平衡代步車控制策略及動力學(xué)仿真 [J].華南理工大學(xué)學(xué)報(自然科學(xué)版),2016,44(1):9-15.
[6] 趙磊.兩輪平衡車建模與系統(tǒng)設(shè)計 [D].成都:西南交通大學(xué),2013.
作者簡介:彭小丹(2000—),女,漢族,安徽合肥人,本科在讀,研究方向:智能機器人控制
收稿日期:2021-04-14

