基于艏艉全參數建模及自航計算的線型優化

陸琛亮， 楊 博， 張淇鑫

(上海船舶研究設計院， 上海 201203)

0 引 言

船舶線型設計與船舶的各項重要指標(油耗、航速、載重量和艙容等)有著密不可分的關系。常規的船舶線型優化設計通常采用軟件手工修改與自動變換相結合的方式進行，通過計算流體力學(Computational Fluid Dynamics，CFD)計算優化減小船體的興波阻力和黏壓阻力，而由于設計周期和計算時間等因素的限制，帶螺旋槳的自航計算一般會省略，取而代之的是通過比較艉部伴流優選多個阻力較小的方案，以期在優選出小阻力線型的同時，提升螺旋槳的工作效率。

本文以一艘低速肥大型散貨船為例進行分析，此類船型的快速性優化往往不能局限于對興波阻力和黏壓阻力進行優化，不同的艉部設計往往會有不同的螺旋槳效率表現，有時甚至有較大的差異。因此，通過自航計算優化降低螺旋槳的收到功率非常必要。本文詳細介紹艏部和艉部全參數建模變換與自航計算相結合的優化方法，最終優化得到螺旋槳收到功率最小的船體線型。

1 目標船基本情況

本文優化的目標船是一艘20萬噸級散貨船，總長約310 m，弗勞德數約為0.139，興波阻力占比較小，此時優化興波阻力對總阻力優化的收效較小，黏性阻力占比較大，且艉部設計不同會導致螺旋槳效率存在較大差異，對于此類船型的優化而言，應對船體總阻力和螺旋槳效率進行綜合優化。

2 船體建模方法

首先需對目標船的艏部和艉部進行參數化建模，建模工具為德國FRIENDSHIP SYSTEMS公司開發的軟件CAESES。該船采用的建模方法同樣適用于集裝箱船和油船等單艉鰭船型。

參數化建模是指通過一系列參數建立船體曲面，這種建模方法的優勢是能通過個別參數的變化迅速變化出具有不同特征的線型，并能直接用于CFD計算，大大增加優化方案的數量，提高優化的效率和效果。

船體建模分為艏部、艉部和舯部(平行中體)等3部分，下面具體介紹參數化建模方法。

2.1 艏部建模

2.1.1 艏部主要參數的名稱及數值

艏部主要參數的名稱和數值：xFp為垂線間長；beam為船寬；draft為吃水；height為型深；bowOverang為球艏長度；xPeak為船體最前端

x

值，等于xFp+bowOverang；xMainFrame為艏部最大橫剖面

x

位置；bilgeHeight為舭部高度；bilgeWidth為舭部寬度；relXFwdBase為平底線前端位置系數；xFwdBase為平底線前端位置，等于xMainFrame+relXFwdBase×(xFp-xMainFrame)。

2.1.2 艏部最大橫剖面的定義

根據上面定義的舭部高度bilgeHeight、舭部寬度bilgeWidth和舭龍骨的豐滿度系數Coeffbilge生成舭部曲線bilge curve，目標船的Coeffbilge取0.805。

2.1.3 艏部各特征曲線的定義

艏部各特征曲線的分類及命名：deck為甲板線；dwl為設計水線；flareAtDeck為甲板處的外飄角分布曲線；flareAtDwl為水線處的外飄角分布曲線；fob為平底線；fos為平邊線；sac為橫剖面面積曲線；stem為艏柱。各曲線形式見圖1。

圖1 艏部初始特征曲線

2.1.4 艏部各曲面的定義

船體曲面構成的原理為：首先通過上述各特征曲線生成CAESES軟件中稱為curve engine曲線的特征函數，然后通過此curve engine沿船長方向生成一條條橫剖線，最后通過CAESES特有的曲面形式MetaSurface連接成光順曲面。這樣所得船體曲面必然滿足上述特征曲線的要求。

但是，由于船舶曲面的復雜性，不可能從最大橫剖面至球艏只用1個特征函數(即curve engine)生成橫剖線，因此按特征曲線的分布，將船體表面分成10個曲面，10個曲面光順過渡連接之后才能形成一個完整的艏部曲面。10個曲面的分類及命名：mid2FosEmerge為從最大橫剖面至設計水線平邊線相交處的曲面；fosEmerge2Fwd為從設計水線平邊線相交處至平邊線最前端的曲面；fosFwd2Base為從平邊線最前端至平底線最前端的曲面；base2Fp為從平底線最前端至艏垂線處，設計水線以上的曲面；fillet為從平底線最前端至艏垂線處，設計水線以下的曲面；topFillet為base2Fp與fillet之間的填充曲面；stem為艏柱附近的曲面；tube為base2Fp與stem之間的填充曲面；bulb1為從艏垂線至其前端1.4 m處的曲面；bulb2為從艏垂線往前1.4 m至球艏最前端的曲面。各曲面形式見圖2。

圖2 目標船各曲面形式

2.2 艉部建模

艉部建模的原理為：首先單獨創建一個不含艉鰭的裸船體，然后建一個艉鰭與裸船體光順過渡，最后去掉裸船體與艉鰭相交處裸船體上多余的部分，形成一個完整的艉部模型。

2.2.1 裸船體艉部主要參數的名稱及數值

裸船體艉部主要參數的名稱及數值：xAftBase為平底線趨勢線后端；xBilgeAft為平底線趨勢線前端，取0.5倍的xMainFrame；xMainFrame為艉部最大橫剖面

x

位置；xTransom為艉封板尾端

x

位置；zTransom為艉封板尾端高度。

2.2.2 裸船體艉部最大橫剖面的定義

最大橫剖面定義與艏部一致，而艉部最大橫剖面所在

x

的位置不同。

2.2.3 裸船體艉部各特征曲線的定義

裸船體艉部各特征曲線的分類及命名：keel為船底基線；fos為平邊線，分前后2段；fob為平底線，分前后2段；deck為甲板邊線，分前后2段；fos_tangent為平邊線進入角，最大為90，分前后2段；bilge_fullness為橫剖線豐滿度，分前后2段。裸船體艉部各特征曲線見圖3和圖4。

圖3 裸船體艉部各特征曲線側視圖

圖4 裸船體艉部各特征曲線俯視圖

2.2.4 艉鰭各特征曲線的定義

就合作學習而言，主要是通過組織開展合作的方式，學習相關知識。新時期，開展語文教學，需要通過分工合作的形式，共同完成學習任務。要運用這種新型的合作學習的教育方式，需要教師對此共同作出努力。在進行合作學習的過程中，要求教師端正自身的態度，采用科學的學習方法，充分應用傳統教學的優點，然后將其與合作學習相結合。不僅要關注學生的學習成績，還要關注其成長過程中出現的一些問題，促使學生在參與合作學習的過程中，學到更多有用的知識。如在大課間的時候，可以組織學生玩“成語接龍”“你比我猜”等游戲，既豐富了學生的課外活動，又能從中學到很多文化知識，增強了學生合作能力，讓其更具有團隊合作意識。

艉鰭各特征曲線的分類及命名：boundary為艉鰭與船體的相交線；intermediate為艉鰭與艉鰭出口端邊線之間的過渡線；boss為艉鰭出口端邊線。艉鰭各特征曲線見圖5。

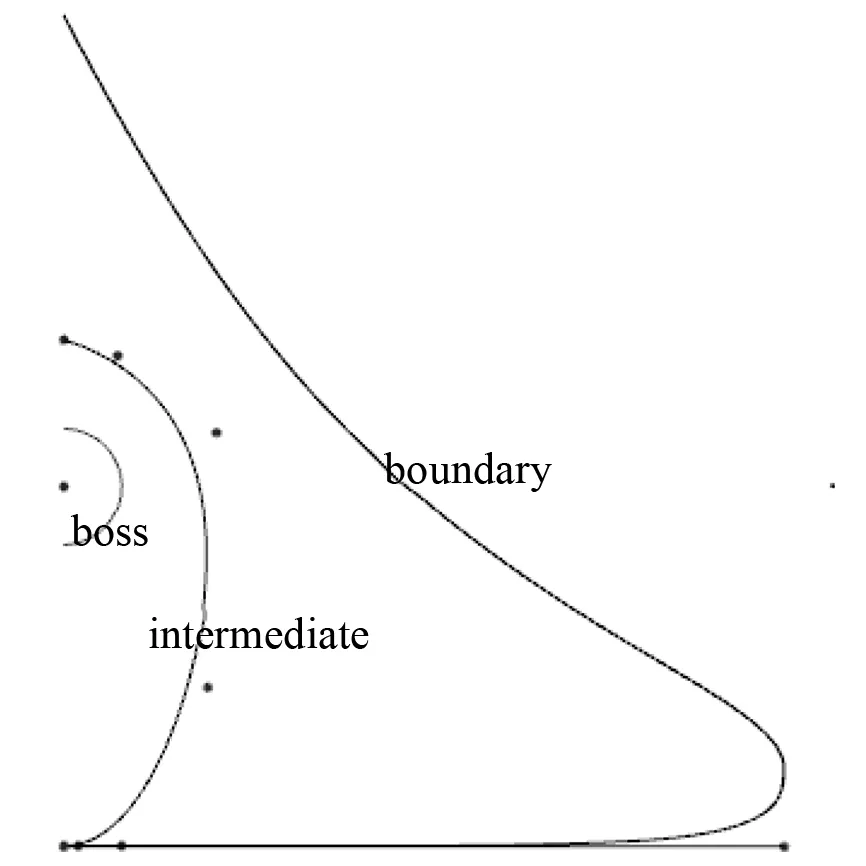
圖5 艉鰭各特征曲線

2.2.5 艉部各曲面的定義

艉部建模得到的2個面見圖6，其中：hull為裸船體；skeg為艉鰭。

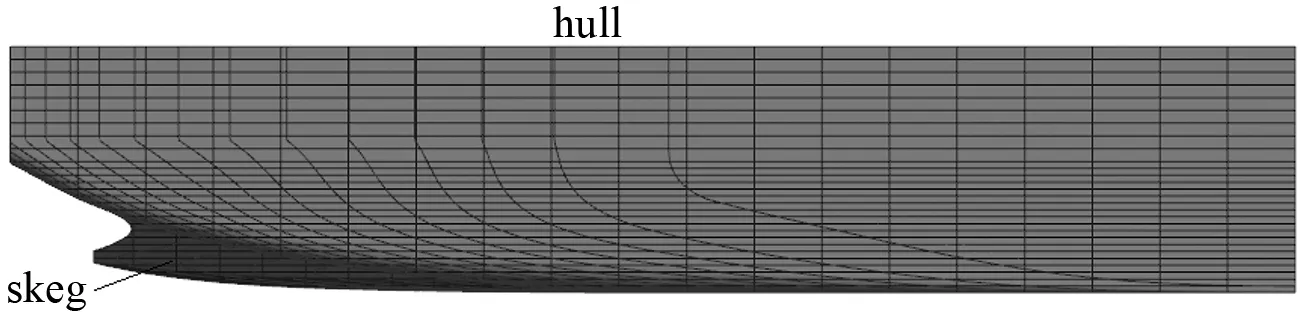
圖6 目標船各曲面的形式

裸船體與艉鰭相交內的裸船體表面需要刪除，從而組成一個完整的帶艉鰭的船體，局部刪除之后的裸船體根據相對于艉鰭的位置分成4個面，其中：behindSkeg為艉鰭后的面；besideSkegAft為艉鰭邊的面(后)；besideSkegFore為艉鰭邊的面(前)；beforeSkeg為艉鰭前的面。最終形成的船體見圖7。

圖7 最終形成的船體

2.3 平行中體建模

平行中體的建模較為簡單，將艏部與艉部最大橫剖面之間的間隙填上即可。

3 全參數優化

3.1 參數變量優化

用于生成船體的參數變量非常多，其中影響船體快速性能的參數變量同樣非常多，因此為提高線型優化的效果和效率，需根據設計者的經驗選取有限的優化變量。

3.1.1 整體參數變量

船體整體變化采用Lakenby變換的方法實現，該方法用于改變橫剖面面積曲線，從而優化浮心縱向位置、排水體積、水線進水角和出水角等重要的線型實現參數。

3.1.2 艏部參數變量

3.1.3 艉部參數變量

艉部優化對于目標船來說至關重要，因此選取較多的參數變量，涉及艉鰭的豐滿度、橫剖面UV度、縱剖線斜度和艉封板尺度等重要船體艉部線型特征。在這些參數中：aft_bilge_fullness_mid為橫剖面最大豐滿度；aft_bilge_fullness_part1為后橫剖面最大豐滿度曲線的豐滿度；aft_cpc2_fullness為船底基線的豐滿度；aft_dk_part1_fullness為后甲板邊線的豐滿度；aft_dk_part1_tangent為后甲板邊線的艉端進入角；aft_fos_tangent_part1為后平邊線的進入角；aft_skeg_width為艉鰭上邊界寬度；aft_width_Factor為艉鰭中間過渡線寬度系數；aft_boundary_fullness為艉鰭上邊界豐滿度；aft_xdeckmax為甲板最大船寬處

x

的最小值；aft_xTransom為艉封板末端的

x

值；aft_yTransom為艉封板末端的半寬值；aft_zTransom為艉封板末端的最小高度。

3.2 船體限制條件

為使優化得到的線型滿足實際的總體及輪機等設計要求，需給定一些限制條件，本文所述目標船主要有以下2個限制條件：

1) 排水體積和浮心位置，通過艏艉模型參數和全局橫剖面面積曲線的Lakenby變換調整；

2) 2個限制點，分別位于主機和貨艙位置，分別在2站和19站位置，通過限制點到船體曲面的最小距離進行判斷，若該距離小于零，則說明限制點在船體曲面之外，即不滿足設計要求。

3.3 優化方法與目標

目標船以設計吃水、15 kn航速為優化點，以降低該狀態下的螺旋槳收到功率

P

為優化目標。優化分2輪進行，其中：第一輪為阻力優化，減小阻力不僅有助于成功實現線型優化，而且能加快阻力計算速度，先進行阻力計算可先對船體進行整體上的優化；第二輪為收到功率優化，即自航計算，2種計算均基于模型尺度進行，模擬水池阻力和自航試驗得到模型尺度下的螺旋槳收到功率

P

，最終優化目標是使螺旋槳收到功率

P

最小。若時間允許，還可進行第二次迭代優化，進一步優化阻力和功率。

用于計算的軟件是FLOWTECH公司的CFD軟件SHIPFLOW，分別包括阻力計算模塊和自航計算模塊。

3.3.1 阻力計算優化

阻力計算采用勢流與黏流相結合的方法，分別采用SHIPFLOW中的XPAN興波阻力計算模塊和XCHAP黏性阻力計算模塊進行計算，目標船的弗勞德數為0.139，模型尺度雷諾數為5.48×10。

由于阻力計算速度較快，黏性計算網格采用global方法生成，網格數相對于自航計算更多，約180萬個。

3.3.2 自航計算優化

自航計算更為耗時，需進行一定的簡化，黏性計算網格采用zonal方法生成，即只對船體后半部分建立黏流計算網格，并進行黏流計算，這樣可大大減少網格數量，縮短黏流計算時間，采用該方法的計算網格數約為50萬個。

SHIPFLOW中的自航計算有3種方法。

1) 固定轉速: 給定轉速計算推力扭矩。

2) 自動：計算阻力，敞水，推力扭曲，尋找推力與阻力的平衡點。

3) 用戶自定義：給定強制力系數，計算速度快。

考慮到僅優化1個速度點的功率，選用第三種方法進行自航計算，設置文件中的Prop命令給定槳盤面的

x

位置、槳軸高度、槳直徑和槳榖直徑，螺旋槳敞水計算采用升力線法，螺旋槳幾何文件需輸入槳葉數、盤面比、0.2～1.0半徑處的螺距比、弦長、厚度和拱度等參數。

3.4 優化算法和優化結果

優化變量的數量較多，艏部變量有5個，艉部變量有13個，變量的組合通過CAESES中自帶的Sobol優化算法生成，針對第3.3節所述的2輪優化，選取不同優化變量和變換范圍，以減少優化方案的計算數量，在進行阻力優化時盡量減少艉部變量的變換范圍，在進行自航優化時減少艏部的變量，把重點放在艉部變量優化上。采用Sobol優化算法生成的變量組合示例見圖8。

圖8 采用Sobol優化算法生成的變量組合示例

進行2輪線型優化之后得到2種線型方案，分別是基于阻力計算優化的線型和基于自航計算優化的線型。

采用SHIPFLOW得到的2種方案的計算結果對比見表1，其中：SHIPFLOW中的興波阻力系數有

C

和

C

2種，

C

由船體表面的壓力得到，

C

通過水面興波得到；

W

為槳盤面處的名義伴流；

C

為摩擦阻力系數；

C

為黏壓阻力系數；

C

為黏性阻力系數，即

C

與

C

之和；

K

為形狀因子；

S

為無因次濕表面積；

P

為螺旋槳收到功率。2種線型方案伴流對比見圖9，線型對比見圖10。

表1 2種方案計算結果對比

圖9 2種線型方案伴流對比

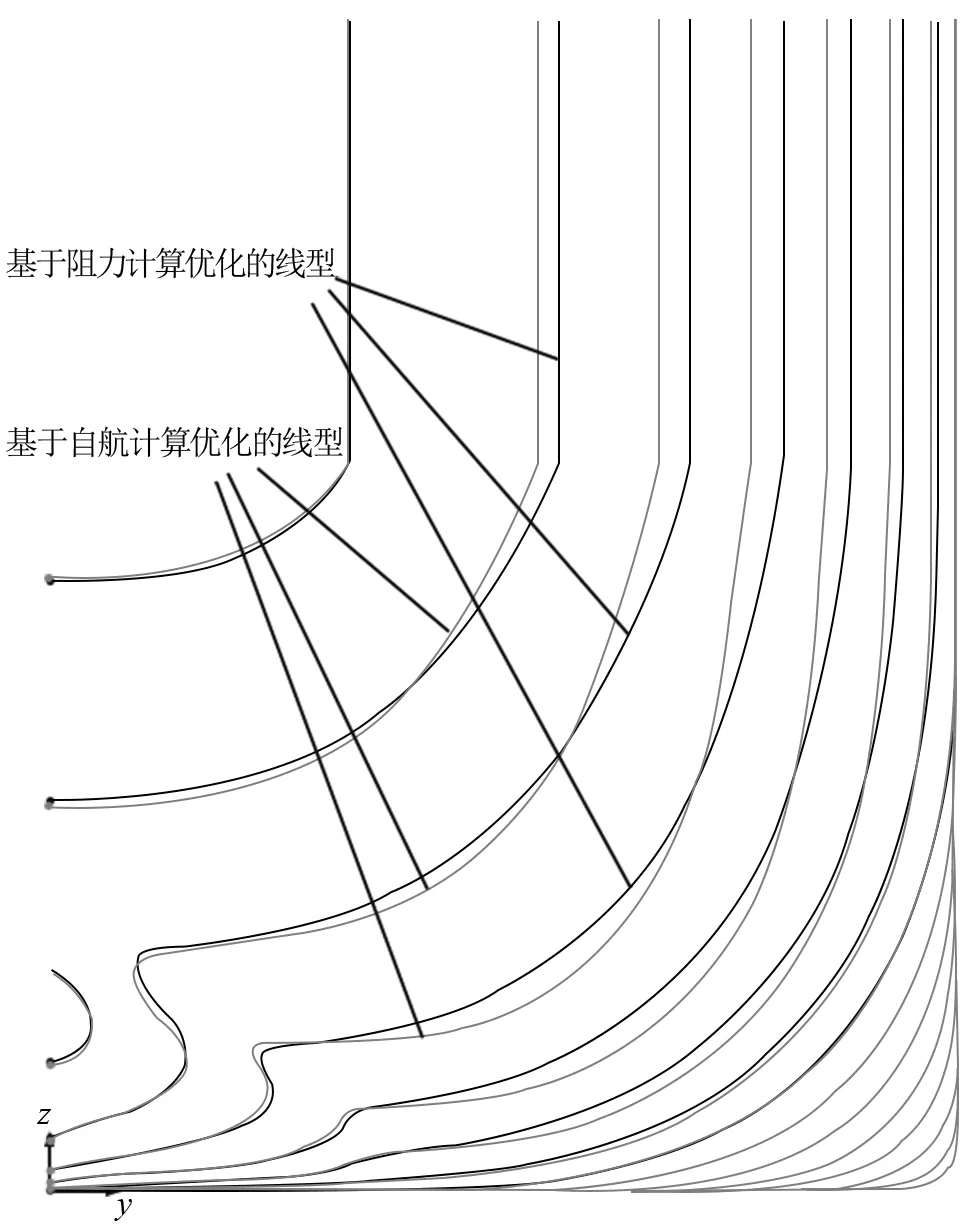
圖10 2種線型方案的線型對比

由計算結果和線型對比分析可知：基于阻力計算優化的線型的黏壓阻力系數比基于自航計算優化的線型的黏壓阻力系數小2.86%，興波阻力系數相當，而基于自航計算優化的線型的艉部外側更為豐滿，伴流稍大，且分布更加均勻，最終的收到功率明顯更小，比基于阻力計算優化的線型小4.2%。由此可知，雖然基于自航計算優化的線型在阻力上并不占優，但由于該線型艉部產生的伴流更有利于螺旋槳推進，使得螺旋槳推進效率較高，最終螺旋槳的收到功率更小，快速性能更優。

4 結 語

船體艏部和艉部全參數建模和變換是進行線型優化的有效方法。阻力計算相對來說速度較快，有利于開展大量方案的優化計算。對經過阻力計算優化的方案進行自航計算優化，目標船的螺旋槳收到功率可進一步減小。同時，參數化變換可設定多種限制條件，從而得到滿足實際使用要求的快速性能更優的模型。