基于模糊單神經元PID 的車載發射裝置隨動控制策略研究

王旭鋒，牛遠征，曾遠帆，殷 翔，姜曉明

（1.南京理工大學 自動化學院，江蘇 南京 210094；2.上海機電工程研究所，上海 201109）

0 引言

隨著現代戰爭模式的迅速變化，戰場上出現越來越多低空、超低空等進攻性武器，這就需要包括車載導彈發射車在內的防空系統具有快速、高精度、準確打擊等能力。作為現代防空體系重要的一環，車載隨動系統的響應速度、跟蹤精度、魯棒性等指標的優劣會直接影響武器系統作戰效能的發揮。

對于發射車的隨動系統而言，由于作戰環境復雜多變，機械摩擦、外部擾動等因素持續存在，動靜態性能也會發生很大變化。在跟蹤目標的過程中，會產生動態滯后，目標速度變化越快，滯后越突出，精確的控制模型往往難以建立。因此，傳統PID 控制已經不能滿足現代戰爭模式的作戰需求［1］。

多年來，許多學者致力于模糊PID、自適應PID、神經網絡PID 等先進PID 控制的研究，用以克服傳統PID 缺陷。其中，模糊PID 控制可以很好地應用于非線性時變系統，但是模型的建立需要大量的經驗，在輸入輸出上受模糊集的影響較大，從而導致系統超調、響應慢等問題［2-4］。自適應PID 控制的好壞，取決于辨識模型的精確度，對于復雜系統是特別困難的［5］。本文提出一種將單神經元與模糊PID 控制相結合的位置隨動控制策略，以兩種控制方法優缺點互補為思路，運用神經網絡控制與模糊控制理論，設計出相應的比例Kp、積分Ki、微分系數Kd的動態調整規則，實現PID 參數的自整定，以此提高系統的快速性、控制精度和干擾能力［6］。

1 車載隨動系統組成及建模

1.1 車載隨動系統組成

車載隨動系統的控制對象為發射裝置，其隨動系統的基本組成如圖1 所示。

圖1 隨動系統的基本組成Fig.1 Basic composition of the follow-up system

伺服計算機是隨動系統的控制中樞，接收來自武控計算機發送的發射裝置方位角、左/右發射架高低角控制指令，經坐標轉換、拉格朗日插值、伺服控制、量綱轉換等步驟，向驅動器發送轉速控制指令［7］。交流（Alternating Current，AC）伺服驅動系統為發射裝置的驅動機構，系統采用三相交流永磁同步電機，用于給發射裝置提供動力力矩。驅動器接收到伺服計算機的轉速控制指令后，經功率放大電路，形成驅動電機的電壓，電機轉動并通過減速器作用于發射裝置。發射裝置的實際位置通過測角裝置發送給伺服計算機，最終形成隨動系統的閉環控制［8］。

1.2 車載隨動系統建模

1.2.1 交流伺服驅動系統建模

交流伺服驅動系統包含有速度環和電流環。速度環為外環，主要用于控制電機轉速。速度環的反饋來自于電機編碼器的旋變信號，經驅動器內部芯片解碼后得到轉速，由驅動器完成速度環的閉環控制。電流環為內環，主要用于控制電機電流，確保電樞電流在啟動瞬間不超過允許值。電流環的反饋來自于驅動器內部安裝在每相的霍爾元件，驅動器采樣電流值后，完成電流環的閉環控制［9］。交流伺服驅動系統工作原理圖如圖2 所示。

圖2 交流伺服驅動系統工作原理Fig.2 Working principle diagram of the AC servo drive system

由于交流永磁電機內部電磁場關系較為復雜，建立數學模型比較困難。因此，在進行隨動仿真時，一般用電樞電壓控制的直流電動機進行。為了簡化電機模型作如下假設：忽略磁場高次諧波影響、電樞回路電感、轉子的繞阻、永磁體的阻尼，以及內部磁場的飽和效應和磁滯帶來的損耗。這樣驅動放大器就可近似成1 個比例環節，執行電機則簡化為一階慣性環節，旋變作為1 個積分環節［10］。由此可得到2 階線性系統模型結構，如圖3所示。

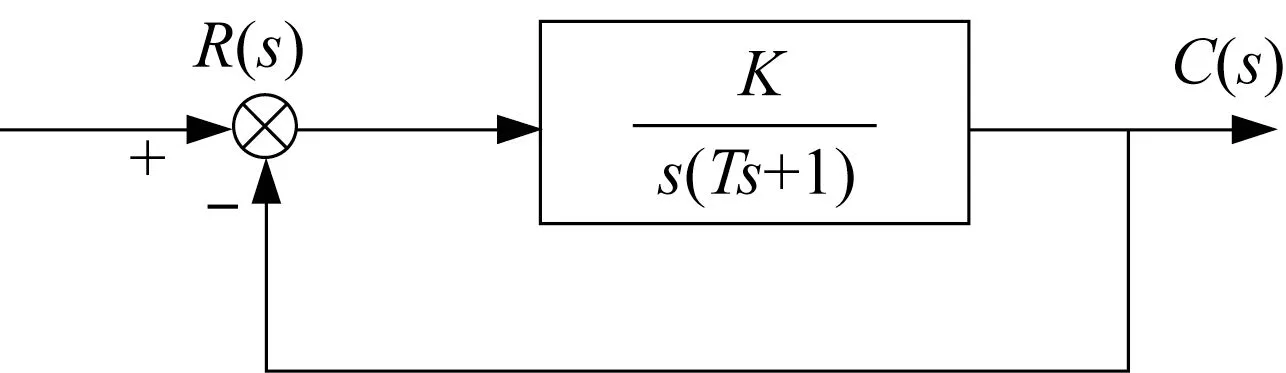
圖3 交流伺服驅動系統等效結構Fig.3 Equivalent structure diagram of the AC servo drive system

圖中，R(s)對應伺服計算機發送的給定轉速，C(s)對應電動機的實際轉速。電機參數、負載慣量以及黏性摩擦系數對參數K、T都有影響。由于參數在工程上難以直接測量和理論計算，一般常采用脈沖響應、階躍響應等方法確定參數數值［11］。本文采用階躍響應法對交流伺服系統進行辨識，即給驅動器發送適當幅值的階躍信號，同時測量電動機的轉速信號，得到速度環響應的超調量σ%和峰值時間tp。根據如下典型2 階系統阻尼比ζ、無阻尼振蕩頻率ωn的公式：

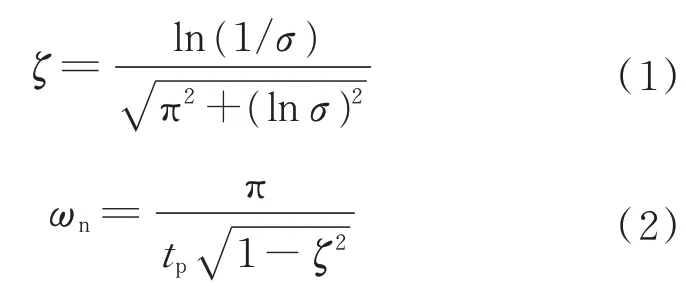
可得到交流伺服驅動系統的傳遞函數為

采用上述方法，以某車載發射車的方位隨動系統為例，多次測得方位隨動系統的超調量與峰值時間，并求均值以后，根據式（1）、式（2）以及傳遞函數公式得到交流伺服驅動系統的傳遞函數為

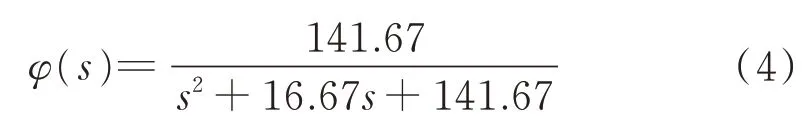
1.2.2 車載隨動系統整體建模

根據車載防空武器隨動系統的組成及工作原理，將隨動系統分為位置環、速度環、電流環，其工作原理圖如圖4 所示。

圖4 車載防空武器隨動系統的工作原理Fig.4 Working principle diagram of the follow-up system for vehicle-borne air defense weapon

以某車載發射車的方位隨動系統為例，減速器是齒輪組合結構，減速比r為120，考慮到角速度單位換算系數100，可得到隨動系統從伺服計算機到轉塔輸出的轉角部分的傳遞函數為

綜上，隨動系統可近似看成1 個含積分環節的3階系統。

2 模糊單神經元PID 控制器

2.1 控制器整體設計

模糊單神經元PID 控制作用于位置環，運行在伺服計算機軟件上。該控制以模糊PID 控制為主體，引入單神經元控制器實時調整參數。然后將兩種算法融合后的kp、ki、kd作用于被控對象，其控制結構如圖5 所示。

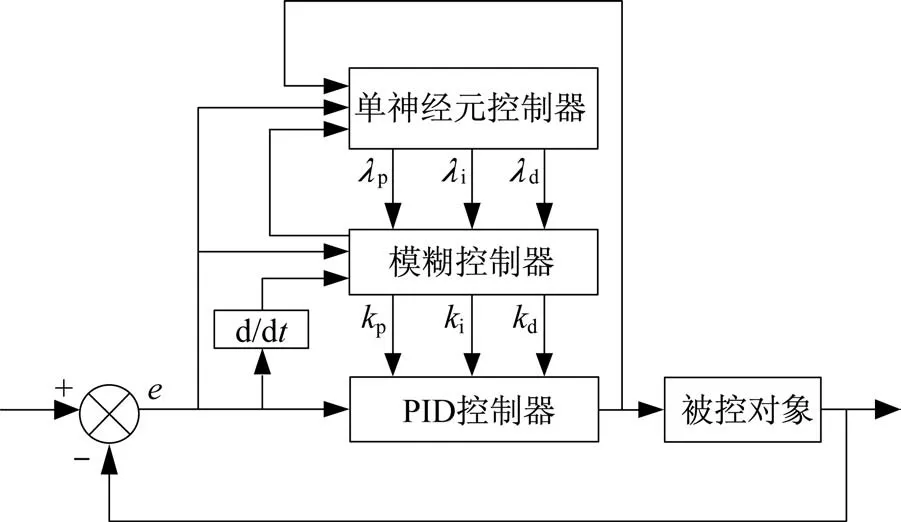
圖5 模糊單神經元PID 控制結構Fig.5 Control structure of the fuzzy single neuron PID

2.2 模糊控制算法

用系統誤差e和誤差變化量ec作為模糊PID 控制輸入，比例系數調節量ΔKp、積分系數調節量ΔKi、微分系數調節量ΔKd作為輸出，利用模糊控制規則在線對PID 參數進行修改，以滿足不同時刻的e和ec對PID 參數自整定要求［12］。

將模糊PID 控制輸入e和ec的變化范圍，定義為模糊集上的論域：e，ec=[-3，3]。其模糊子集為e，ec=[NB，NM，NS，ZE，PS，PM，PB]，子集元素分別代表“負大”“負中”“負小”“零”“正小”“正中”“正大”。對輸入進行尺度變換后，使輸入量映射在設定的論域內，目的是對輸入模糊化。對輸出而言，比例系數調節量ΔKp、積分系數調節量ΔKi、微分系數調節量ΔKd的論域分別設置為[-3，3]、[-1，1]、[-1，1]，ΔKp、ΔKi、ΔKd均服從正態分布。以比例系數調節量ΔKp為例，其隸屬度函數如圖6所示。

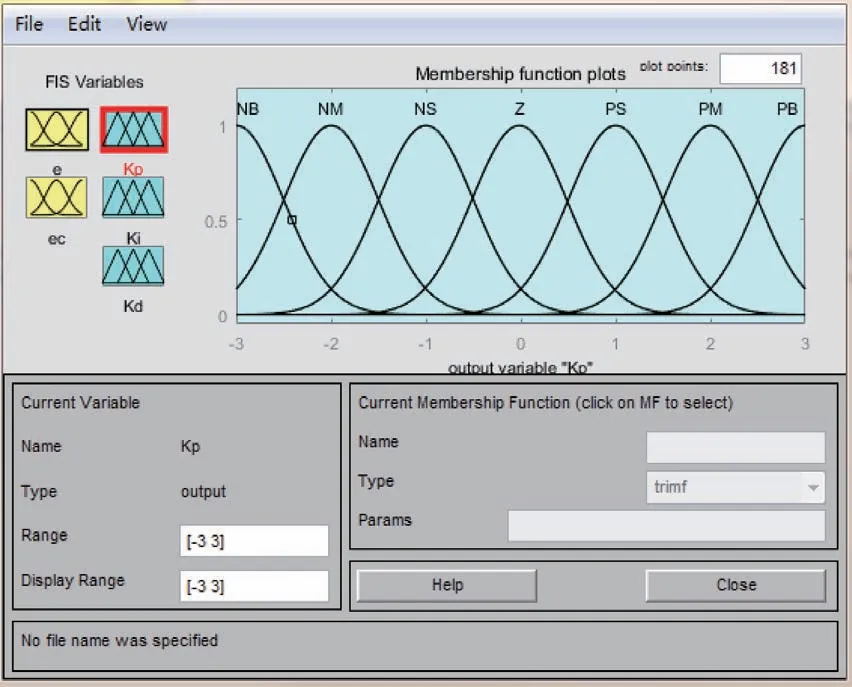
圖6 隸屬度函數設置Fig.6 Setting of membership functions

考慮到不同時刻，3 個參數對系統作用以及3 個參數之間的相互影響，模糊PID 控制在PID 控制的基礎上對輸入模糊化，并根據模糊規則進行模糊推理，查詢模糊矩陣表進行參數調整。制定規則如下：當轉塔執行角度偏轉指令開始，為提高響應速度，增大比例系數，減小微分系數作用；在中后期，增大積分系數，適當減少比例和微分系數的作用［13］。由此建立輸入輸出的模糊規則表，見表1。

表1 模糊規則表Tab.1 Fuzzy rule table

由表1 以及隸屬函數，可得到輸出模糊子集的隸屬度。解模糊的方法有最大隸屬度法、重心法、加權平均法等。本文采用重心法進行反模糊化，使輸出為具體值［14］，計算公式如下：

式中：μi(e)為系統誤差e的隸屬度；μj(Δe)為系統誤差Δe的隸屬度；fij為輸出參數的隸屬度；u為模糊控制器的輸出；μij為所屬的隸屬模糊子集，其值由模糊規則表確定。

模糊輸出參數公式如下：

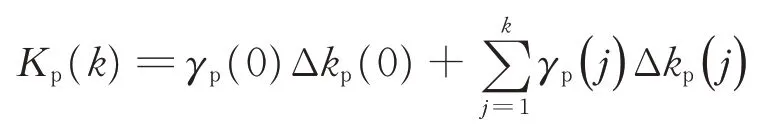
式中：Δkp（0）、Δki（0）、Δkd（0）為PID 控制參數初值；γp（j）、γi（j）、γd（j）為模糊輸出的修正參數的比例系數；γp（0）、γi（0）、γd（0）為比例系數的初值。

2.3 單神經元控制算法

神經網絡模擬是根據人腦的思維方式確定的數學模型，主要用于解決復雜的非線性、不確定系統。根據有監督的Hebb 學習規則，利用輸入和輸出調整神經元之間連接的權值，設計出自適應控制器［15］，其結構如圖7 所示。

圖7 單神經元結構圖Fig.7 Diagram of single neuron structure

具體算法如下：

式中：ηp、ηi和ηd分別為比例P、積分I、微分D 的學習系數；UPID為PID 控制器的輸出。其中，學習系數的制定一般按照經驗選取。

3 仿真試驗及結果分析

通過Matlab/Simulink 工具建立隨動控制系統仿真模型，并加入模糊PID 控制、模糊單神經元PID控制進行仿真對比。對于發射車隨動控制系統的參數，在實際調試過程中，一般運用斜坡信號、正弦信號進行調節［16］。為了驗證模糊單神經元PID 算法的有效性，用函數信號發生器分別產生階躍信號、正弦進行仿真驗證。根據對車載隨動系統的數學建模、模糊單神經元PID 控制器設計，可設計仿真結構如圖8 所示。

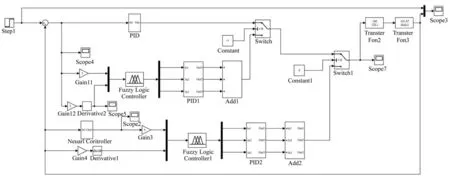
圖8 系統Simulink 仿真結構Fig.8 Simulation structure diagram of the system by Simulink

圖8 中，Fuzzy Logic Controller為模糊邏輯控制器，Neuarl Controller為單神經元控制器，Derivative為微分環節，Transfer Fcn為辨識出來的傳遞函數。通過Switch 控件選擇，分別實現模糊PID 控制與模糊單神經元PID 控制對傳遞函數的仿真，并對兩者的輸出結果進行對比。

在車載發射裝置運動過程中，隨動控制系統一般存在最優路徑選擇，即最大調轉角度為180°。在仿真試驗中，選取初值γp（j）、γi（j）、γd（j）為2.87、0.38、0.19。選取ηp、ηi和ηd學習系數分別為0.35、0.009、0.05。分別設置模擬輸入幅值為90°、180°的階躍信號，幅值為45°，周期為6.28 s 的正弦信號，并查看模糊PID 控制、模糊單神經元PID 控制的仿真結果，仿真結果如圖9～圖11 所示，其中，橫坐標為時間，縱坐標為發射裝置調轉的角度。

圖9 幅值為90°的階躍信號的仿真結果Fig.9 Simulation results of the step signal with amplitude of 90°

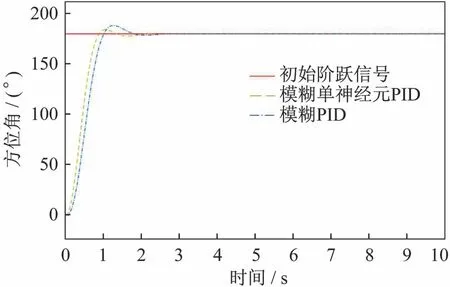
圖10 幅值為180°的階躍信號的仿真結果Fig.10 Simulation results of the step signal with amplitude of 180°

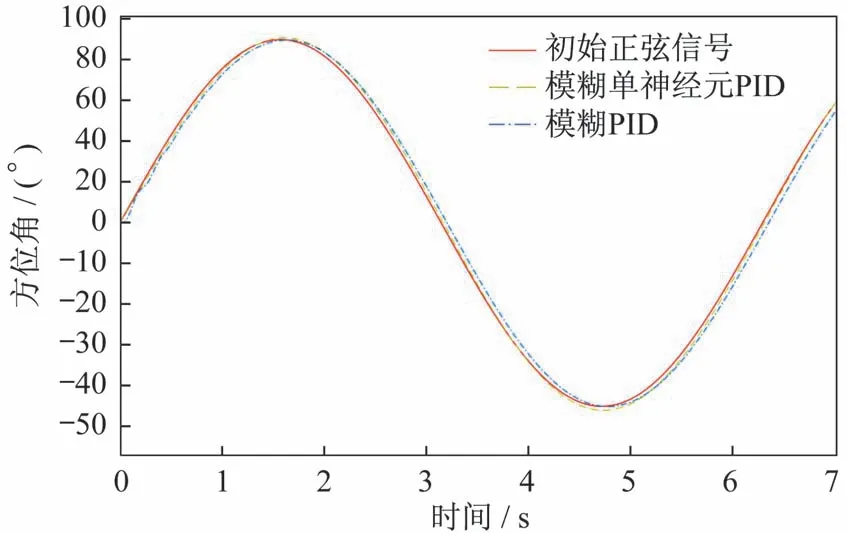
圖11 幅值為45°、周期為6.28 s 的正弦信號的仿真結果Fig.11 Simulation results of the sinusoidal signal with amplitude of 45° and period of 6.28 s

通過分析對比2 個控制器的控制性能，整理結果見表2 和表3。

表2 幅值為90°、180°的階躍信號的控制性能Tab.2 Control performance of the step signal with amplitude of 90° and 180°

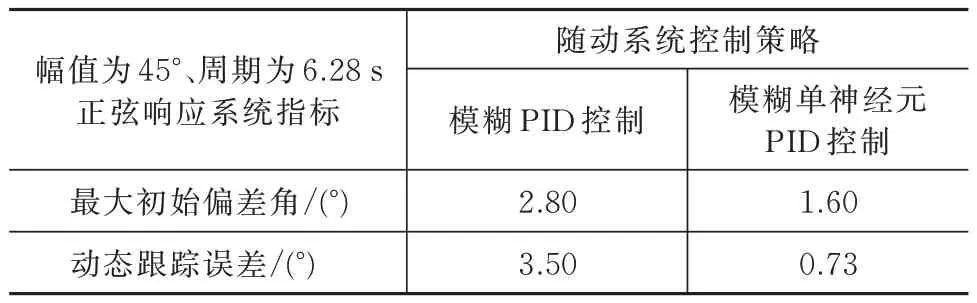
表3 幅值為45°、周期為6.28 s 的正弦信號的控制性能Tab.3 Control performance of the sinusoidal signal with amplitude of 45° and period of 6.28 s

綜合仿真結果和分析得出：對于階躍信號，模糊單神經元PID 控制器相比傳統模糊PID 控制器響應速度要快，且超調量明顯縮小；對于正弦信號，模糊單神經元PID 控制的最大初始偏差角以及動態跟蹤誤差均優于模糊PID 控制。經過對傳統模糊PID 控制的改進，模糊單神經元PID 控制器具有一定的學習能力和自適應能力，使得發射裝置能夠快速、準確、穩定地控制、執行隨動控制指令，各項性能指標均達到系統作戰要求。

4 結束語

本文對發射車隨動系統的控制策略進行研究。首先，根據車載隨動系統的組成及工作原理進行數學建模，并運用系統辨識及理論分析，得到車載隨動系統的傳遞函數；其次，運用神經網絡控制與模糊控制理論，以兩種控制方法優缺點互補為思路，設計了單神經元模糊控制的學習規則，將單神經元與模糊PID 控制相結合的隨動控制；最后，運用Matlab 中的Simulink 進行仿真。仿真結果表明，相比于傳統模糊PID 控制，模糊單神經元PID 控制可以顯著提高發射裝置的靜態、動態跟蹤性能，驗證了該隨動控制策略的可行性。