向量鍵合圖在平面多體系統建模中的應用研究*

單東升，梁 全，牛 彪

(沈陽工業大學機械工程學院，遼寧 沈陽 110870)

0 概述

復雜系統建模和仿真，通常可能涉及到多領域交叉的建模和仿真工作。隨著科技的發展，機械領域的分析與控制變得愈發重要。傳統的機械系統分析方法大多數只是單獨一種能量形式的系統，不能適用于多領域交叉的耦合系統。

鍵合圖是多能域統一建模的一種有效工具，它能統一各種能域，只用一種理論就可以建立完整的機電液混合系統的模型，是實現多領域交叉的復雜耦合系統進行動態分析建模和仿真的有效方法[1]。傳統鍵合圖理論已經發展成熟，在液壓系統、電氣系統、機械系統以及風力發電等領域的建模仿真中都有著不錯的表現[2-5]，然而在對多體系統進行建模時還存在很多問題。

多體系統由數量有限的剛體組成，通過任意關節相互連接。由于多體機械系統存在多剛體相互作用，因此剛體間存在運動幾何約束，使得鍵合圖模型內部存在很多非線性的結型結構。進行運算時需要反復迭代方程，出現微分因果環，所以此時傳統鍵合圖法還不適合在計算機上進行全局動力學分析。許多學者為此提出了一些解決辦法，這些方法在對復雜機械系統的描述過程中，通過標量鍵合圖建立的模型會非常繁瑣、復雜，從而對分析求解模型的過程造成阻礙，容易出錯。多維度的鍵合圖可以彌補標量鍵合圖的不足，并成為了近些年鍵合圖理論的研究熱點，例如針對于雙曲柄六桿壓力機構動力學仿真問題的向量鍵合圖法[6]、圍繞Delta型3D打印機多能域耦合動力學建模的旋量鍵合圖法[7]等。

諸多研究熱點中，向量鍵合圖具有結構簡潔、形式緊湊的優點，但是長期以來國內外對于向量鍵合圖的研究大多數局限于多體系統的圖形表示，應用于模型仿真時需要分解成標量形式，從而再次導致了復雜的圖形模型，失去了其緊湊圖形的優勢。同時關于向量鍵合圖與計算機自動建模仿真相結合的實現，研究空間還很大。本文針對這些不足，對基于向量鍵合圖的多領域復雜系統建模和仿真進行了研究。

本文提出了三種針對平面多體系統進行建模的向量鍵合圖基礎模型：自由剛體的向量鍵合圖模型，兩種速度轉換的向量鍵合圖模型。基于容性元的特性方程得到了各種運動關節的向量鍵合圖模型的搭建方法。由此，分別搭建了單擺模型，雙缸并聯平臺模型，并在20-sim軟件中對模型進行仿真，仿真結果證明建模的合理性。

1 基于向量鍵合圖的基礎模型介紹

基于三維的向量鍵合圖理論，分別建立自由剛體模型及兩種速度轉換模型，共三種基礎模型。通過容性元特性方程限制運動關節的自由度，得到各種運動關節的向量鍵合圖模型。對以上模型進行封裝，模塊化。

1.1 自由剛體模型

自由剛體的表示基于牛頓-歐拉方程，經過變矢量的絕對導數與相對導數定理的轉換，可以得到：

(1)

對應式(1)建立自由剛體的向量鍵合圖模型如圖1所示。

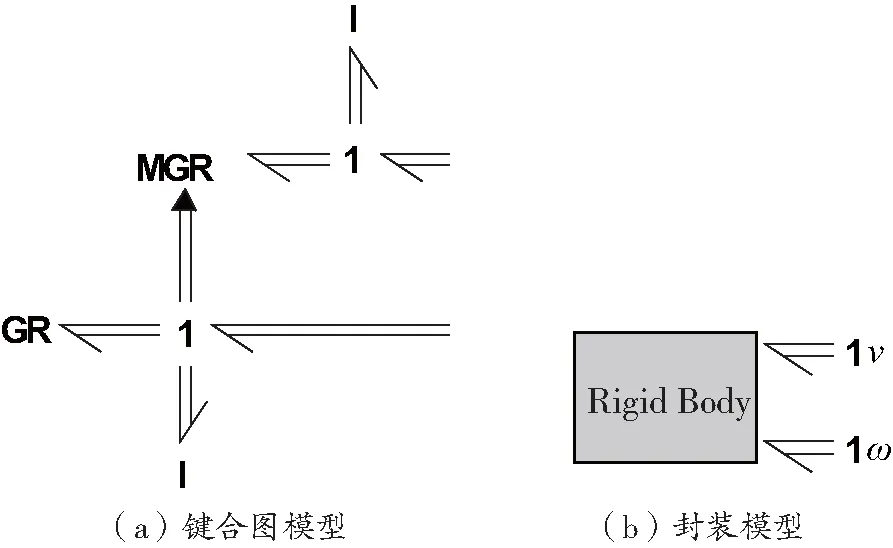
圖1 自由剛體向量鍵合圖模型

較高的共流結代表慣性系中的質心速度向量v，前者連接表示剛體慣性的慣性元；較低的共流結代表質心角速度向量，前者連接表示剛體主軸轉動慣量的慣性元；自制的MGR元件與GR元件的值為：

MGR：ω×(m·v)

(2)

GR：ω×(J·ω)

(3)

1.2 速度矢量轉換模型

速度矢量的轉換分為兩種，一種是剛體內部任一點處速度矢量的轉換，另一種是不同坐標系間的速度矢量轉換。

基于基點法可求得剛體內任一點的速度，因此，勢變量對應的方程為：

M=F×r

Mi=εijkFjrk

(4)

流變量對應的方程為：

v=ω×r

vi=εijkωjrk

(5)

式(4)與式(5)符合變換器形式，因此剛體內的任意兩點A和B的速度矢量轉換的向量鍵合圖模型如圖2所示。

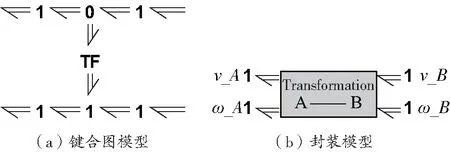
圖2 剛體內部兩點速度矢量轉換

不同坐標系間的速度矢量轉換是指速度矢量在剛體的體固坐標系與運動關節的中間坐標系(各軸與慣性系平行)之間的相互轉換。本文采用歐拉角法實現了這種轉換，如式(6)所示。歐拉角α、β和γ定義了三種連續有序的旋轉：γ是繞z軸旋轉的角度，β是繞y軸旋轉的角度，α是繞x軸旋轉的角度。對體固坐標系中的速度矢量依次左乘α、β、γ三個歐拉角旋轉矩陣便可得到中間坐標系中的速度矢量，三個歐拉角旋轉矩陣相乘可以寫成相應的正交變換矩陣，如式(7)所示。

ωG=Tω

vG=Tv

(6)

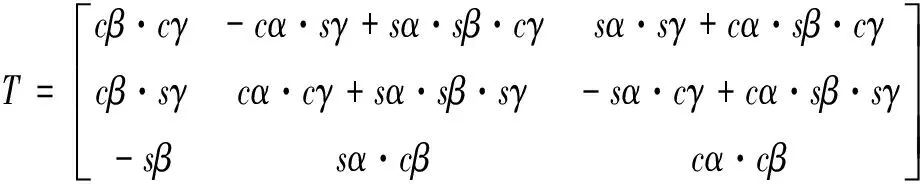
(7)

式中：ωG、vG—中間坐標系的角速度與線速度；ω、v—體固坐標系中的角速度與線速度；c=cos,s=sin。

因此速度矢量從體固坐標系轉換到中間坐標系的向量鍵合圖模型如圖3所示。

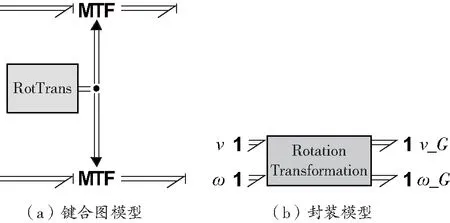
圖3 坐標系轉換模型

圖3中的RotTrans模塊內置正交變換矩陣，輸入信號是經過體固坐標系中角速度調制的歐拉角。

1.3 運動關節的實現

運動關節是剛體間的連接部分，它需要限制了空間中的一些自由度，本文是基于設置容性元來實現的，容性元的特性方程為：

(8)

其中：e(t)—勢變量；q(t)—流變量；C0—線性容度參數。

容性元內置參數設置非常小時，容性元所連接的鍵上勢變量與流變量的值都近似為0，在容性元上鍵接一個共勢結(與共勢結連接的鍵上勢相同，流之和為0)，因此當共勢結與容性元連接的鍵上流近似為0時，與共勢結連接的另兩條鍵上的流數值是近似相等的。通過這樣設置容性元，使得關節具有一定的柔性而不是完全剛性，取越小的容性元參數，運動關節的剛度越大；反之，取越大的容性元參數，運動關節的柔性越大。

以繞x軸轉動的轉動關節為例，轉動關節只有一個方向上轉動的自由度不受限制，其向量鍵合圖模型如圖4所示。

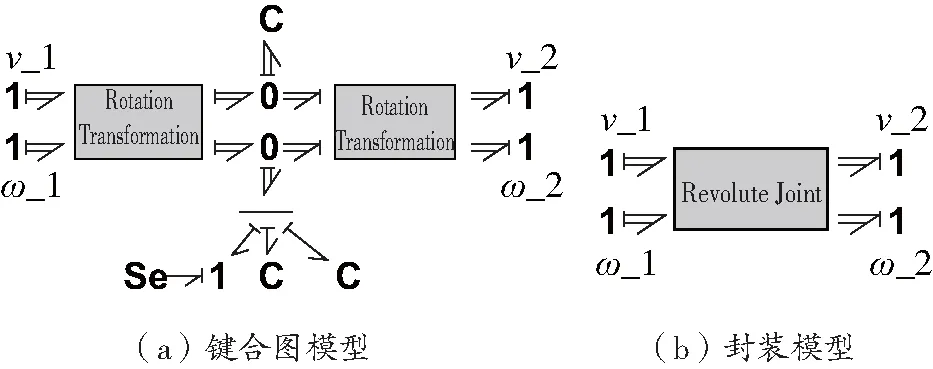
圖4 轉動關節的向量鍵合圖模型

1.4 模型驗證

假設某單擺長為0.1 m，左端點A點固定在坐標原點上，右端點為B點，單擺在YOZ平面內與OY軸成-30°；單擺質量為0.065 kg，轉動慣量為4.4×10-5kg·m2，不計阻尼，在YOZ平面在重力作用下做單擺運動，該單擺模型在Amesim軟件中如圖5(a)所示，其未完全模塊化的向量鍵合圖模型如圖5(b)所示。

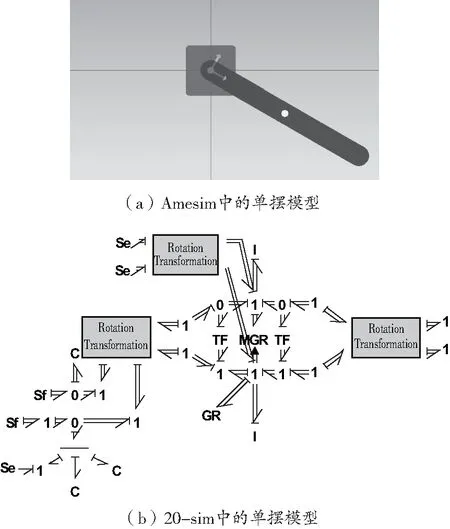
圖5 單擺模型

兩個勢源通過坐標系轉換施加到單擺剛體的質心上，以此模仿重力；單擺左端通過旋轉關節與兩個流源Sf=0連接，起到將單擺左端點與地面固連的作用。

需要對3個坐標系轉換子模型的內置正交變換矩陣右乘一個矩陣：

[1,0,0;0,sqrt(3)/2,0.5;0,-0.5，sqrt(3)/2]

以此對應單擺與OY軸成-30°，在20-sim軟件中輸出仿真曲線如圖6所示。

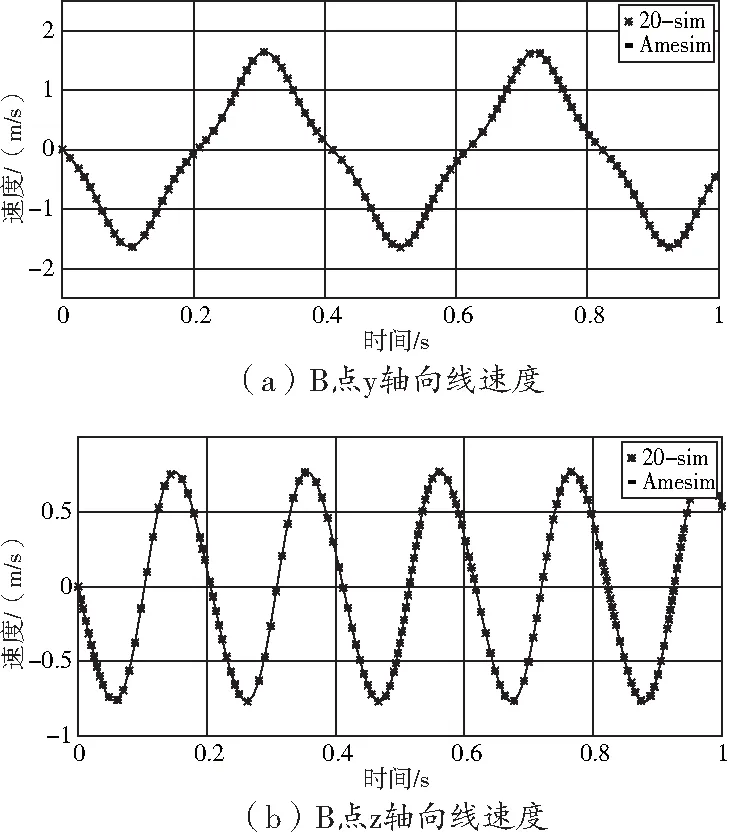
圖6 單擺模型位移輸出曲線

兩個模型的曲線輸出結果一致，驗證了曲柄滑塊的向量鍵合圖模型的正確性。

2 雙缸并聯平臺多能域耦合建模與仿真

2.1 雙缸并聯平臺的向量鍵合圖模型

某雙缸并聯平臺的簡圖如圖7所示，左驅動桿不可以轉動，橫梁長為L，左右驅動桿未伸縮時的自由長度為r，由兩個閥控缸控制平臺的姿態，平臺系統的自由度是2。

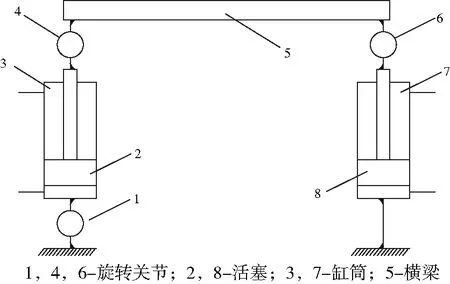
圖7 雙缸系統示意圖

閥控缸通過傳統鍵合圖進行建模，在此不進行詳述[8]，閥控缸的模型與平臺的多體模型通過一個伸縮關節連接，如圖8所示。

圖8 伸縮關節的向量鍵合圖模型

通過容性元限制了3個轉動和2個平動的自由度，允許兩個連接剛體在z軸方向上的兩個極限點之間存在相對移動，圖7中的剛體內部轉換子模型通過液壓缸的極限位置端點進行了調制；勢源在這里代表液壓缸的作用。

輸入期望姿態信號通過自編運動學反解模塊輸出信號到閥控缸，閥控缸采用閉環PID控制；雙缸多體系統按照結構功能進行一次封裝，其一級子模型如圖9(a)所示其子模型命名對應于圖7中編號；通過系統功能進行二次封裝，其主模型如圖9(b)所示，通過逐級封裝，模塊化的雙缸并聯平臺的模型變得非常簡潔。

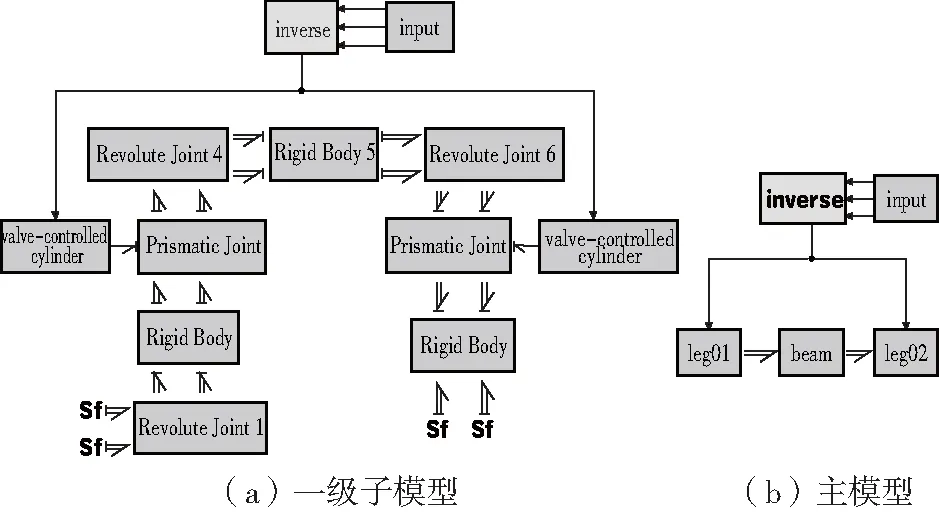
圖9 20-sim中的雙缸并聯平臺

2.2 算例

給定雙缸并聯平臺多體結構部分的尺寸參數：橫梁長及左右驅動桿未伸縮時的自由長度分別為L=5 m，r=3 m，初始位置時兩個驅動桿與橫梁垂直，橫梁負載為5000 kg。輸入期待值alpha=0.2 rad，y=0.05 m，z=0.5 m。

此時平臺質心位姿及雙缸狀態的輸出如圖10所示。

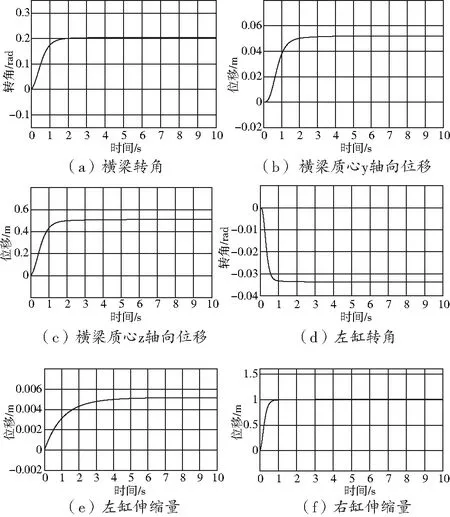
圖10 仿真輸出曲線

平臺質心的輸出曲線穩態值與輸入的期待位姿信號一致，運動學反解算法與平臺模型互相驗證正確，運動學反解模塊輸出信號與雙缸伸縮量一致，說明平臺的多體結構建模正確，對平臺的控制成功。

3 結論

基于向量鍵合圖理論，提出了3種針對多體動力學系統進行建模的基礎模型。文中以單擺模型為例，驗證了3種基礎模型以及通過容性元限制運動關節自由度的正確性；以雙缸并聯平臺為研究對象，實現了多體系統與閥控缸系統相結合的多領域統一建模與仿真。

研究結果表明：

1)提出的向量鍵合圖基礎模型對多體系統的表達意義清晰，輸出正確，可用來表達任何平面多體結構；通過對基礎模型與各種運動關節進行封裝，實現模塊化建模，形式更簡潔。

2)以本文基礎模型搭建的雙缸并聯平臺多體結構的向量鍵合圖模型與閥控缸的傳統鍵合圖模型結合，實現對雙缸并聯平臺系統的建模與仿真驗證。基于本文所述基礎模型，可以與其他傳統的標量鍵合圖模型連接，用統一的方式處理多能域耦合的平面多體系統的動力學分析問題。