基于熱傳遞作用的環空圈閉壓力預測與分析

曾思佳 何 淼，2 周 卓 黃千慧 李金璐 張 更

(1. 長江大學石油工程學院， 武漢 430100；2. 非常規油氣湖北省協同創新中心(長江大學)， 武漢 430100)

深水油氣開發條件嚴苛、地質復雜、安全問題突出，其中由井筒流體熱傳遞導致的環空圈閉壓力上升是深水油氣井鉆采過程中面臨的諸多難題之一[1-2]。在深水油氣田開發過程中，特別是高溫高壓油氣井測試及生產初期，幾乎所有的井都會出現環空帶壓現象。這是由于地層流體溫度高達上百攝氏度，而海床附近溫度很低，熱的地層流體在流經生產管柱時使得井筒溫度場重新分布，熱傳遞作用會引起環空流體即完井液溫度升高，當密閉環空流體受熱膨脹卻又無法釋放壓力時，就形成了環空圈閉壓力[3-4]。圈閉壓力的產生會誘發套管變形，嚴重時甚至導致套管破裂、油氣井報廢[5]。前人針對環空圈閉壓力預測已開展了大量研究工作[6-11]，分析主要集中在溫度及流體特性對圈閉壓力的影響，分析的因素較為局限。因此，根據PVT狀態方程及彈塑性力學理論，建立深水油氣井環空圈閉壓力模型，綜合分析環空圈閉壓力與環空溫度、環空流體膨脹、壓縮系數及套管的泊松比、線性膨脹系數、彈性模量、壁厚之間的關系。研究結果可為深水油氣安全高效開發及其井筒完整性保障提供參考。

1 環空圈閉壓力形成機理

環空是指兩層套管柱之間未被水泥封固的空間。典型的深水鉆井四層套管井筒傳熱示意圖見圖1。A環空為油層套管和生產管柱之間的空間；B環空為油層套管與技術套管之間的空間；C環空為表層套管與技術套管之間的空間[12]。環空圈閉壓力上升主要突出在油氣井生產、測試初期，這段時期環空中的流體溫度迅速增加，同時造成各個環空圈閉壓力不斷升高，當圈閉壓力增加至套管抗外擠或抗內壓強度極限時，就會導致套管損壞或上頂井口，給深水油氣井安全高效生產帶來巨大障礙[13]。在整個過程中，井底儲層產出的高溫流體是井筒溫度上升的源頭，環空流體則是壓力產生的載體。

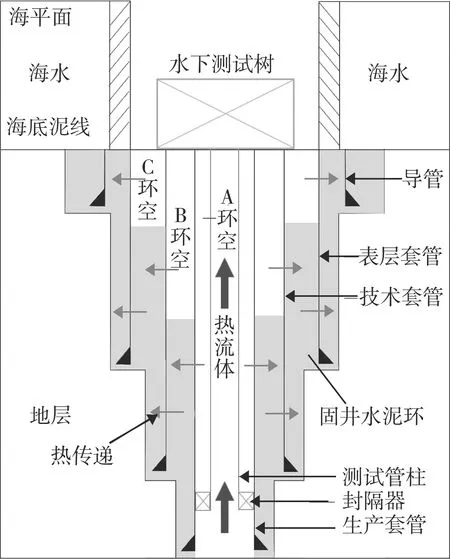
圖1 深水井筒傳熱示意圖

2 環空圈閉壓力模型的建立

環空圈閉壓力模型控制單元示意圖如圖2所示。對長度為L的密閉環空，令向下為正方向，模型控制單元上端為海底泥線，下端為水泥返高。在模型的建立過程中，對模型進行如下假設：

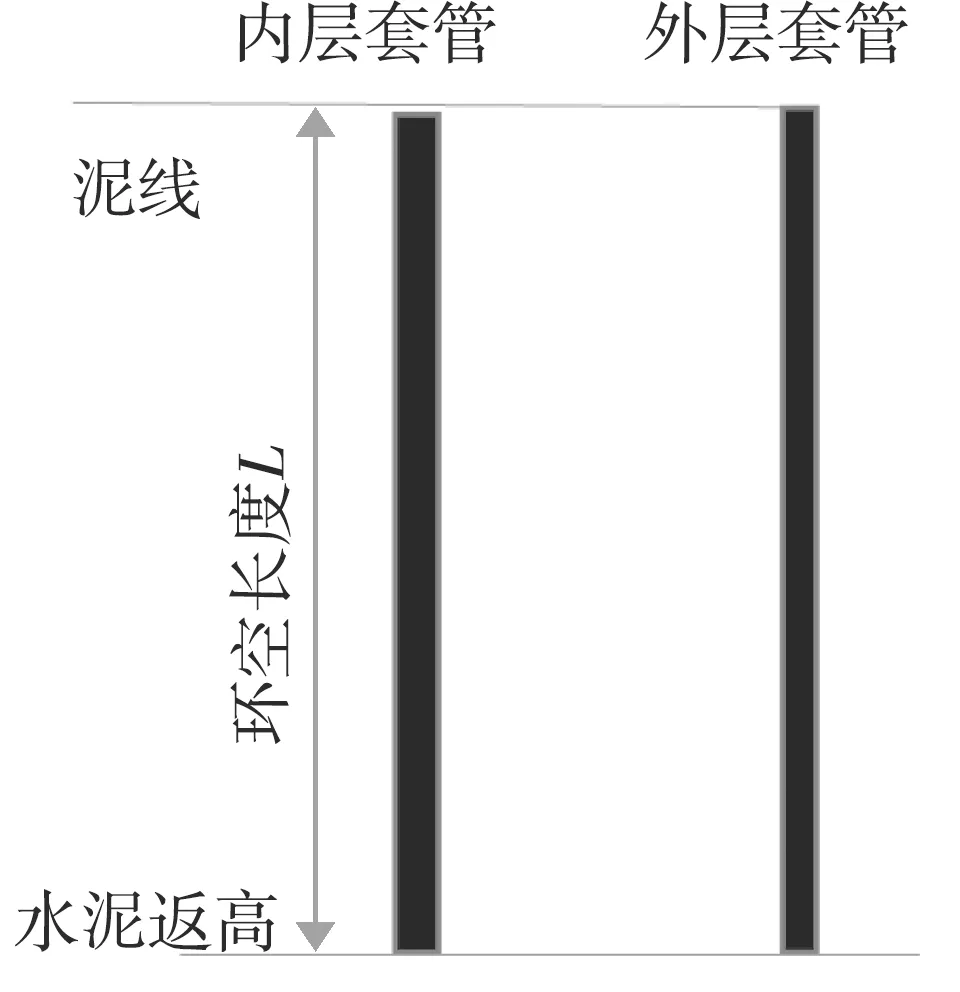
圖2 環空圈閉壓力模型控制單元示意圖

(1) 環空密閉且充滿流體。

(2) 模型只考慮在生產過程中由熱效應引起的環空圈閉壓力上升。

(3) 模型只考慮內層套管的變形。

(4) 套管材質均勻、軸對稱，且物性參數不受時間、溫度的影響。

(5) 深度相同的環空流體溫度變化相同。

環空圈閉壓力上升的原理類似于石油地質學中的“水熱增壓”原理[14]，即井筒中高溫流體的熱量傳遞到環空以后，內外層套管之間的環空和環空流體體積同時發生改變，原本有限的環空體積難以容納受熱體積膨脹的流體。基于體積相容性原則，環空圈閉壓力增加使環空流體受壓縮效應的影響，最終實現流體體積與環空體積相等。由于環空是密閉的且充滿流體，則在生產的過程中環空體積與環空流體的體積始終保持相等，即

ΔVft-ΔVfp=ΔVa

(1)

式中：ΔVft為環空液體受熱膨脹產生的體積變化量，m3；ΔVfp為環空液體受壓收縮產生的體積變化量，m3；ΔVa為環空體積變化量，m3。

環空流體體積的變化主要是受溫度、壓力的影響，分別表示為

ΔVft=αVfΔT

(2)

ΔVfp=kVfΔP

(3)

式中：α為環空流體的等壓膨脹系數，℃-1；k為環空流體的等溫壓縮系數，MPa-1；ΔT為環空中溫度的平均變化量，℃；ΔP為環空中的壓力變化量，MPa；Vf為環空流體的總體積，m3。

將式(2)(3)帶入式(1)中可得

(4)

環空體積變化[15]主要包括：套管熱膨脹的體積變化、套管壓縮的體積變化、環空流體熱膨脹的體積變化、環空流體壓縮的體積變化。

(1)內層套管受熱徑向膨脹導致的環空體積變化量ΔVn1為

(5)

式中：rno為n環空內層套管外徑，m；un1為n環空內層套管受熱膨脹的徑向位移，m；Ln為n環空長度，m；下標n是指A、B、C環空。

其中，內層套管受熱膨脹產生徑向位移un1為

(6)

式中：αs為內層套管線性膨脹系數，℃-1；rni為n環空內層套管內徑，m；μ為內層套管材料泊松比。

(2)內層套管受環空壓力增加導致的環空體積變化量ΔVn2為

ΔVn2=π[(rno+un1)2-

(rno+un1-un2)2]Ln

(7)

其中，內層套管受壓縮產生的位移un2為

(8)

式中：E為內層套管彈性模量，MPa。

(3)環空流體受熱膨脹所引起的體積變化量ΔVn3為

(9)

式中：rmi為n環空外層套管內徑，m。

(4)環空流體受壓縮所引起的體積變化量ΔVn4為

(10)

因此，n環空總的體積變化量ΔVn為

ΔVn=-ΔVn1+ΔVn2+ΔVn3-ΔVn4

(11)

3 環空圈閉壓力模型求解

環空圈閉壓力模型采用迭代的方法，利用MATLAB編程實現環空溫度、體積耦合的圈閉壓力計算。模型計算過程為：首先假設ΔVa=0，利用式(4)計算環空壓力增量ΔP；然后將ΔP代入式(5)～(11)中計算出環空體積變化量ΔV；再將ΔV代入式(4)中，計算出一個新的環空壓力增量ΔPc，將ΔP與ΔPc進行比較，如果滿足精度的要求就輸出結果，反之重復上述的過程，直到滿足要求為止。模型計算流程框圖見圖3。

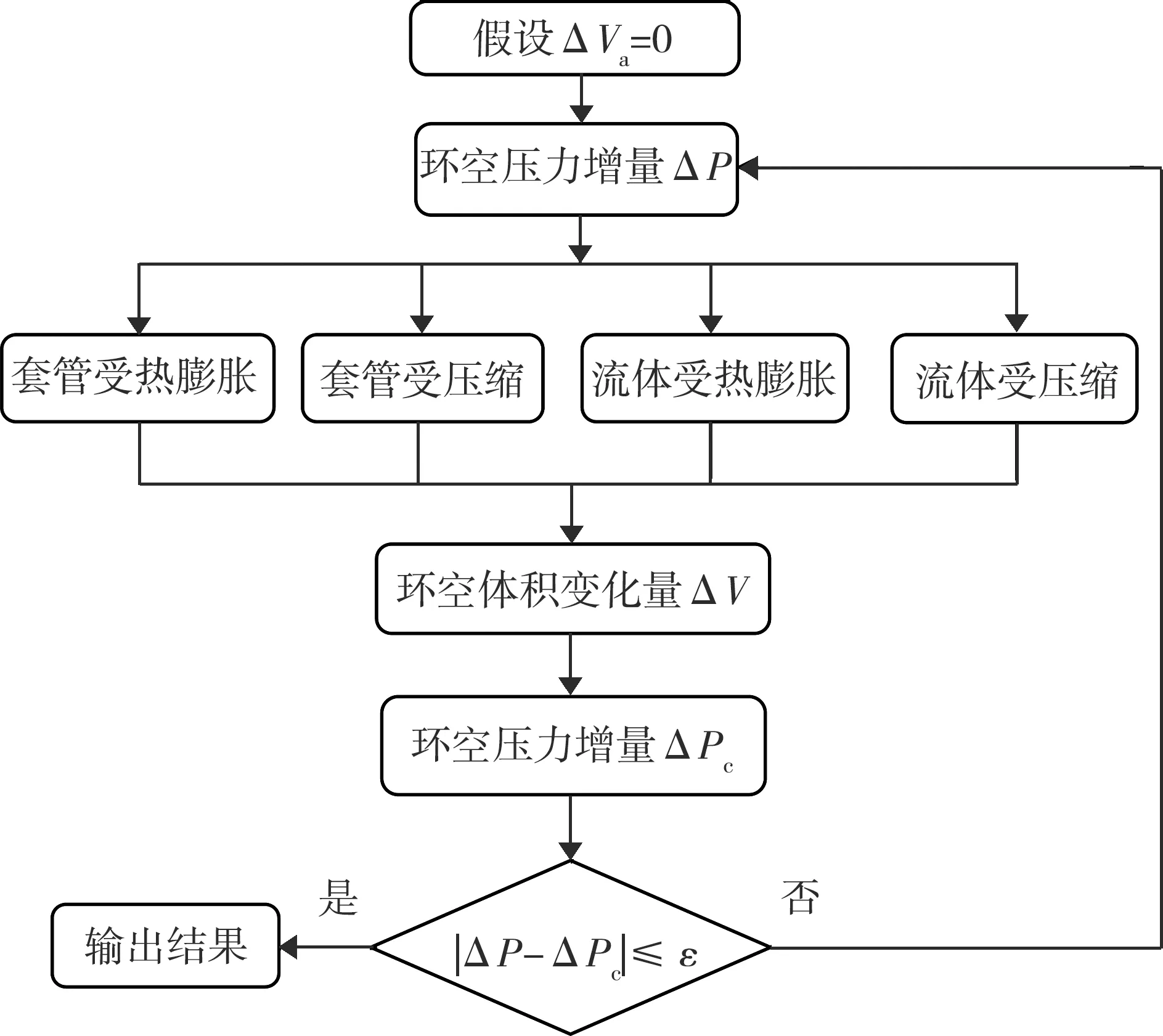
圖3 環空圈閉壓力模型計算流程框圖

4 計算與分析

采用一口典型的深水油氣井進行環空圈閉壓力計算，分析環空溫度增量、環空流體膨脹壓縮系數及套管參數對其的影響。井身結構參數見表1，其余計算所需參數見表2。

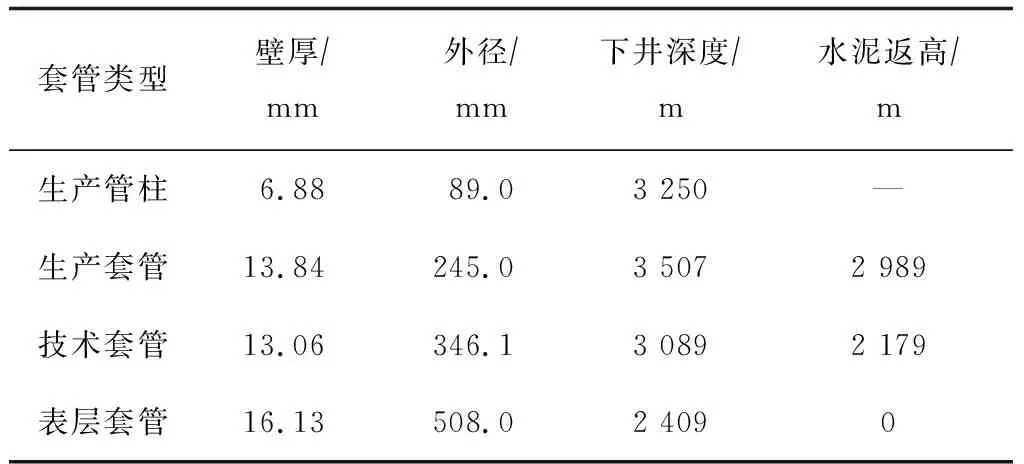
表1 井身結構參數

表2 計算參數

4.1 環空溫度增量對環空圈閉壓力的影響

模擬得到不同的環空溫度增量下的環空圈閉壓力，如圖4所示。從圖中可以看出，環空圈閉壓力隨環空溫度的增加而上升，且B、C環空的圈閉壓力明顯比A環空的圈閉壓力高。當環空溫度每增加10 ℃時，A、B、C環空圈閉壓力分別上升9.9、11.1、11.6 MPa。

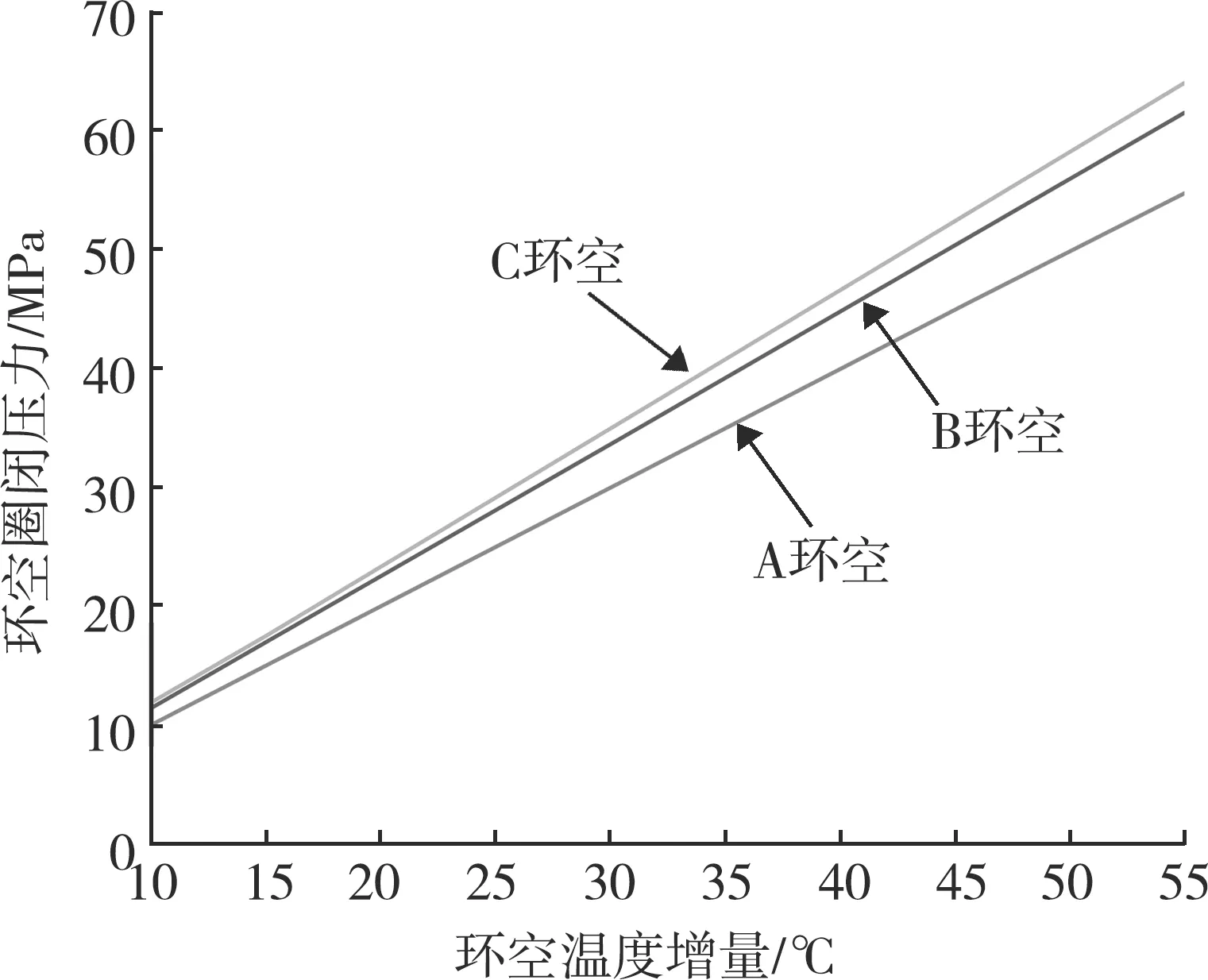
圖4 環空溫度增量與環空圈閉壓力的關系曲線

4.2 環空流體膨脹、壓縮系數對環空圈閉壓力的影響

環空流體受熱膨脹是產生圈閉壓力的主要原因，通過計算得到不同的流體膨脹系數下的環空圈閉壓力，如圖5所示。從圖5可以看出，隨著環空流體膨脹系數的增加，環空圈閉壓力逐漸上升。這是由于流體膨脹系數越大，環空流體受熱膨脹的體積增量就越大，流體受熱膨脹的體積無法釋放，就會在環空中產生圈閉壓力。環空流體膨脹系數對B、C環空的影響要大于A環空。

圖5 環空流體膨脹系數與環空圈閉壓力的關系曲線

環空流體壓縮系數與環空圈閉壓力之間的關系如圖6所示。隨著流體壓縮系數的增加，環空圈閉壓力逐漸降低。這是由于環空流體壓縮系數越大，流體越容易壓縮，環空圈閉壓力越容易釋放。當流體壓縮系數在(2～5)×10-4MPa-1變化時，環空圈閉壓力下降較快，此時流體壓縮系數對環空圈閉壓力影響較大；當流體壓縮系數大于6×10-4MPa-1時，各環空圈閉壓力下降變緩，此時的流體壓縮系數對環空圈閉壓力影響較小。因此，我們在固井作業中可以適當采用壓縮系數高、膨脹系數低的完井液體系。

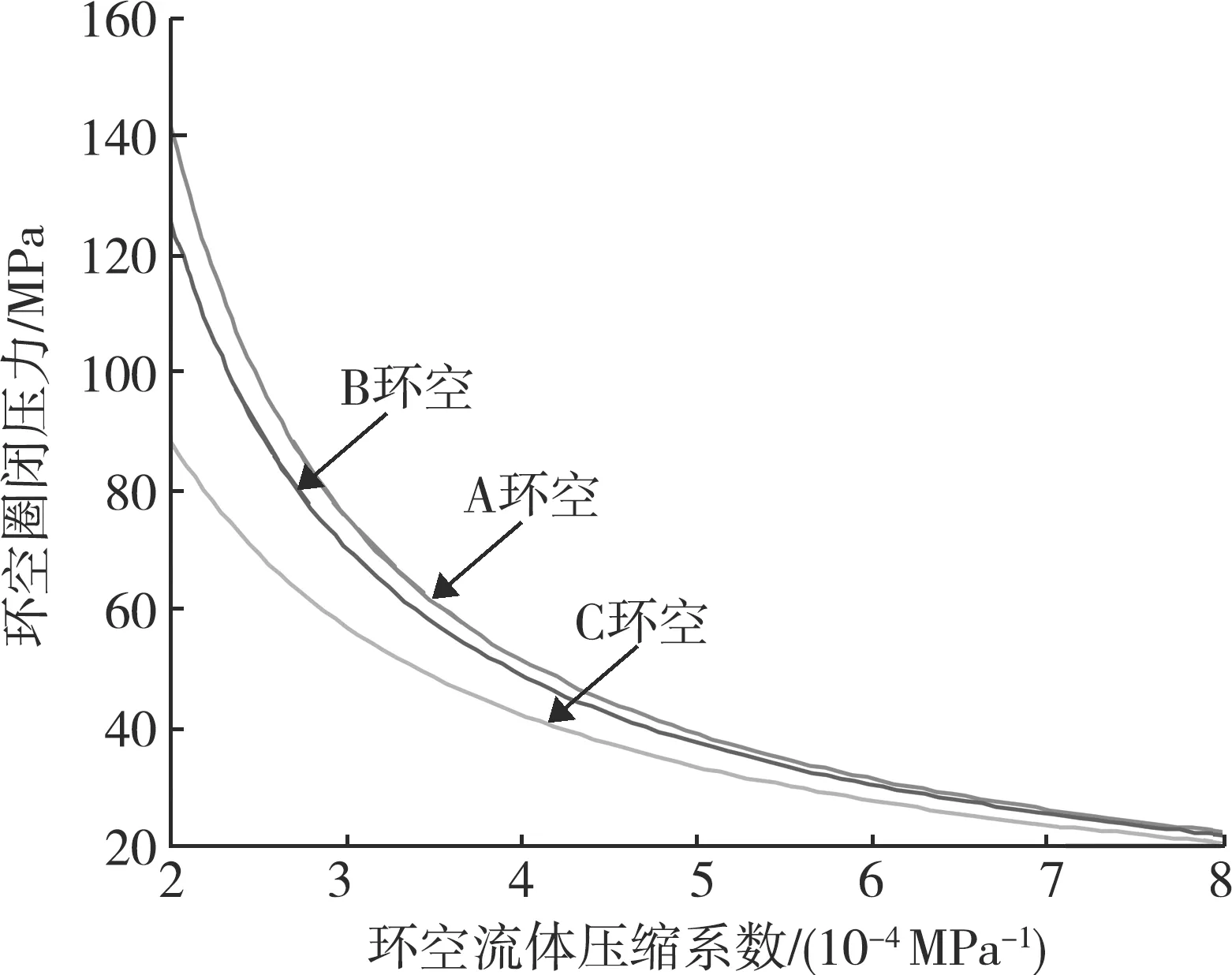
圖6 環空流體壓縮系數與環空圈閉壓力的關系曲線

4.3 套管參數對環空圈閉壓力的影響

計算得到不同的套管泊松比、彈性模量下的環空圈閉壓力，如圖7、8所示。可以看出，環空圈閉壓力隨著套管泊松比和彈性模量的增加而降低。

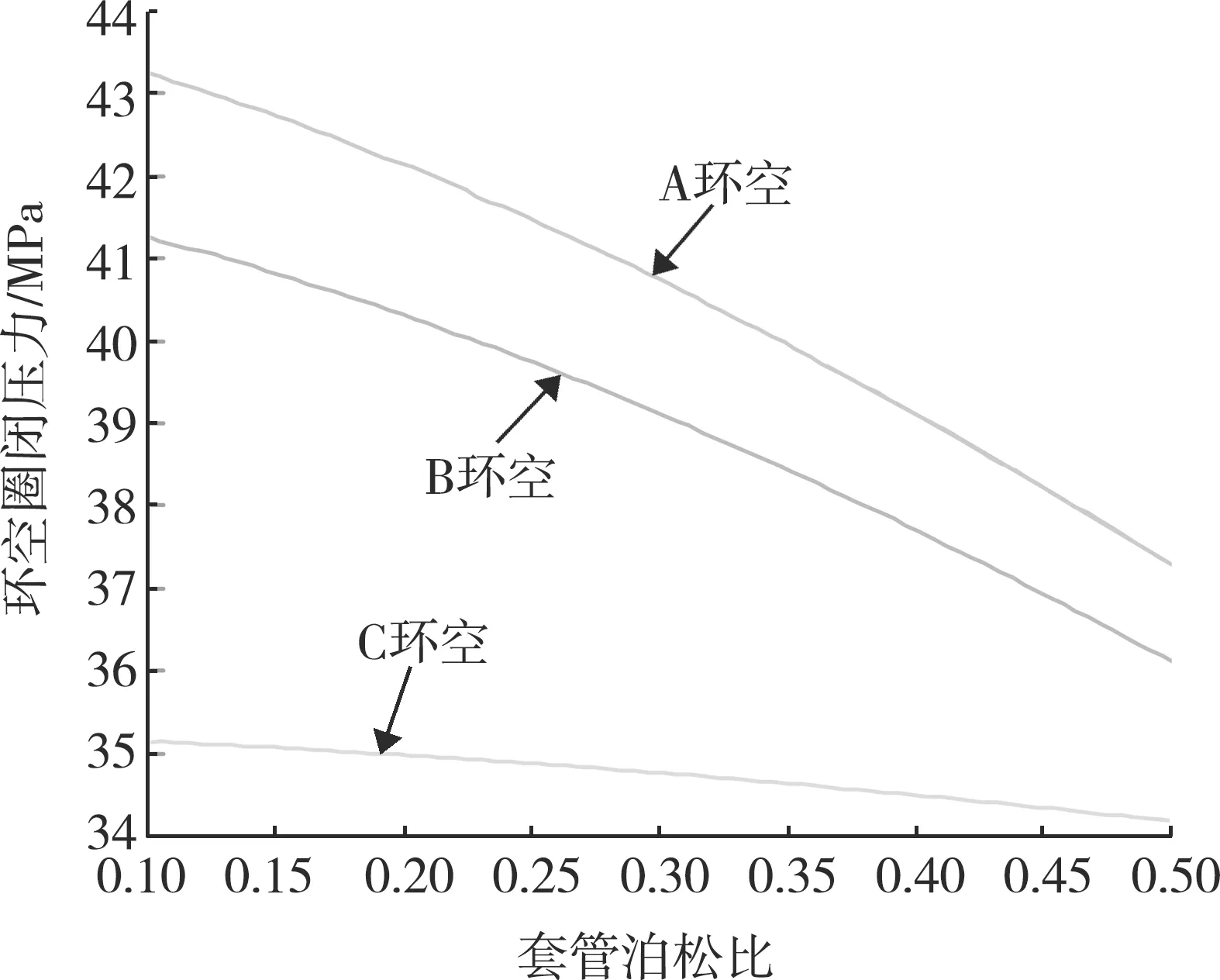
圖7 套管泊松比與環空圈閉壓力的關系曲線

計算得到不同的套管線性膨脹系數、不同壁厚下的環空圈閉壓力，如圖9、10所示。可以看出，隨著套管線性膨脹系數的增加，環空圈閉壓力呈減小趨勢，但總體變化不大。套管線性膨脹系數對A、B、C環空圈閉壓力影響均較小，而套管的壁厚對B、C環空圈閉壓力影響較大，隨著套管壁厚的增加，環空圈閉壓力逐漸增大。

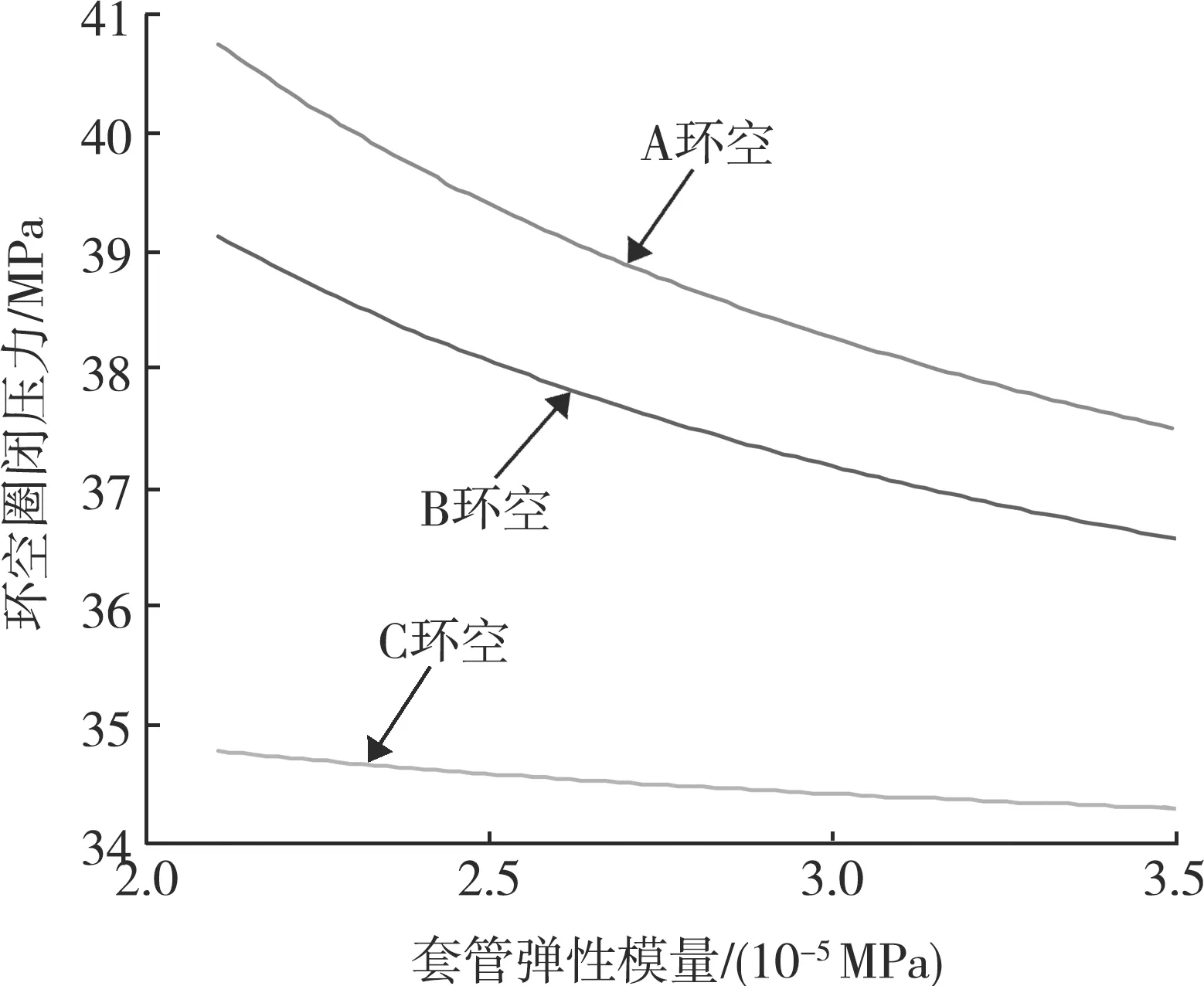
圖8 套管彈性模量與環空圈閉壓力的關系曲線

圖9 套管線性膨脹系數與環空圈閉壓力的關系曲線

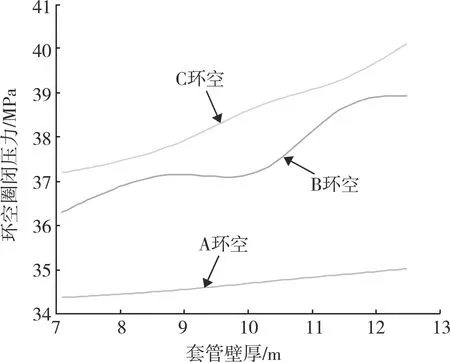
圖10 套管壁厚與環空圈閉壓力的關系曲線

4.4 誤差分析

繪制了在不同的環空溫度增量下的迭代次數與誤差的關系曲線，如圖11所示。這里的誤差是指每次計算的ΔP與上次計算結果的絕對差值。從圖11可以看出，計算誤差是逐漸變小、逐步收斂的。這說明利用迭代的方法進行模型求解是可行的。隨著溫度的增加，迭代次數逐漸增加，收斂變緩。當溫度為30 ℃時，迭代次數為140次；當溫度為40 ℃時，迭代次數為144次。

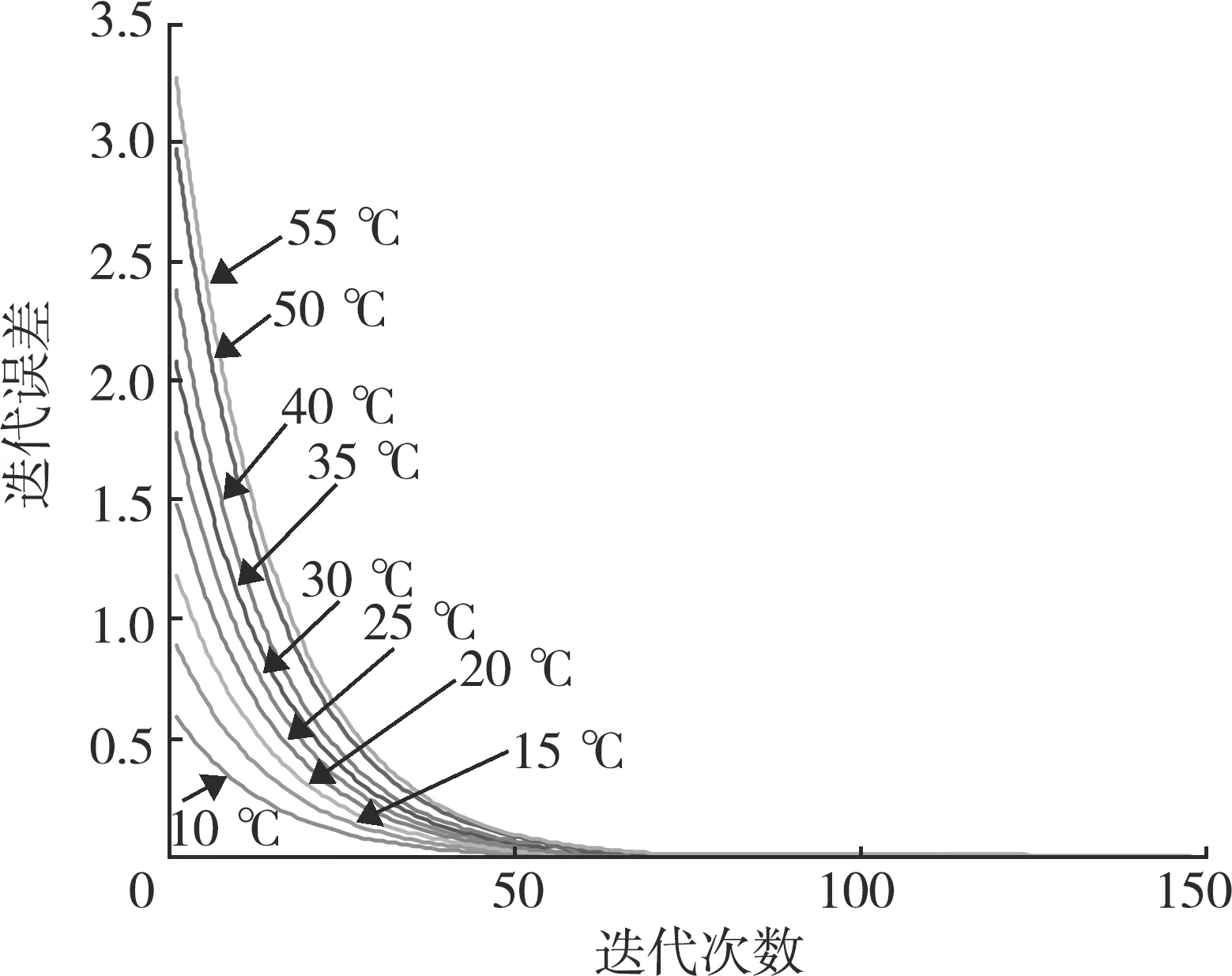
圖11 迭代次數與誤差的關系

采用文獻[16]中的實驗數據進行模型驗證，結果如表3所示。對比發現，模型計算結果與實驗數據平均誤差在6.6%左右。這說明建立的模型的計算結果與測量數據吻合較好，有較高的精度。

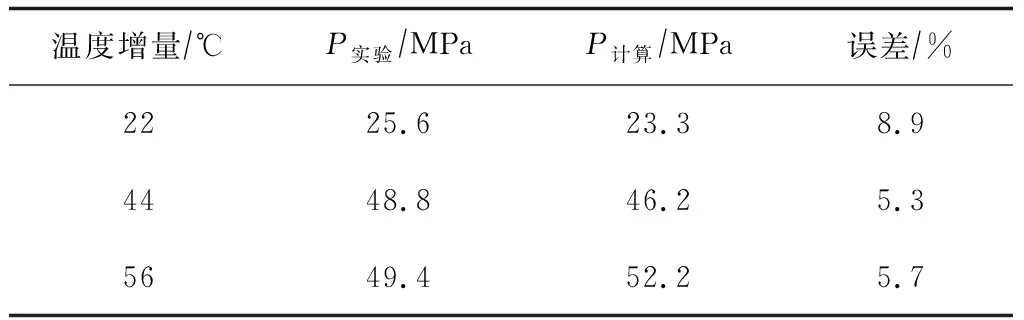
表3 模型計算結果與實驗數據對比

5 結 語

基于PVT狀態方程和彈塑性力學理論，建立了考慮環空溫度、體積耦合變化的環空圈閉壓力預測模型，并采用MATLAB編程和迭代法對模型進行求解。計算結果表明，隨著環空溫度的增加，環空圈閉壓力逐漸升高。分析環空流體的壓縮、膨脹系數對環空圈閉壓力的影響，發現隨著流體壓縮系數的增加，環空圈閉壓力逐漸減小；而隨著流體膨脹系數的增加，環空圈閉壓力逐漸增大。分析套管的基本參數對環空圈閉壓力的影響，發現隨著套管泊松比、彈性模量的增加，環空圈閉壓力逐漸減小；隨著套管壁厚的增加，環空圈閉壓力逐漸增大；線性膨脹系數對環空圈閉壓力的影響較小。進一步開展模型計算過程中迭代誤差分析，發現迭代結果逐步收斂，且隨著溫度的增加，迭代次數也逐漸增加，迭代結果收斂變緩。