地球表面測向交叉定位算法

趙辰乾，王松波，劉益辰

(中國船舶工業系統工程研究院，北京 100094)

0 引 言

目標定位在戰爭中具有重要意義，確定目標位置有助于了解敵方的軍事部署，進而為武器打擊提供引導。電子偵察通過被動接收輻射源目標的電磁信號來確定目標位置，具有作用距離遠、隱蔽接收、不易被敵方察覺的優點。無源定位方法主要有測向交叉定位法和時差定位法。測向交叉定位法無需進行精確的時間同步且只需進行信息級的數據協同，但是定位精度較低。時差定位法需要進行精確的時間同步且需要信號和脈沖級的數據協同，但是定位精度較高。本文主要研究測向交叉定位算法。

測向交叉定位方法已經非常成熟，經典算法有幾何定位法、最小二乘法[1]、離散概率密度法[2]和最大似然法[3]等，但是這些經典算法都基于二維平面場景，沒有考慮地球曲率的影響，在實際應用中，對遠距離目標和高緯度目標的定位誤差過大。目前，眾多學者也提出了許多基于地球表面的交叉定位算法。文獻[4]提出了基于橢球模型的定位算法，該算法計算復雜度低且系統誤差極小，但是只適用于兩站交叉定位場景。文獻[5]提出了基于地球橢球參考平面的定位算法，該方法可以部分消除地球曲率的影響，但是需要額外參考點，且對參考點的選取非常敏感，選取不當的參考點時，定位誤差很大[6]。除此之外，還可以采用迭代法求解非線性定位方程組，但是該方法具有計算量大、存在迭代不收斂情況、無解析解等問題。針對上述問題，本文提出了基于距離誤差最小和地球表面約束的交叉定位算法，算法適用于雙站和多站場景，對于遠距離目標和高緯度目標的系統定位誤差極小，同時具備有解析解、無需迭代等優點。

1 算法原理

本文提出的交叉定位算法基于距離平方和最小準則和地球表面約束，即定位點位于地球表面且距離各偵察站測向面的距離平方和最小。本算法是一種典型的最優化問題，可用拉格朗日乘子法進行求解。

假設共有M(M≥2)個偵察站參與交叉定位，第i個站的經度為Li，緯度為Bi，高度為Hi，測向方位角為φi。

首先，計算各偵察站的地心地固(ECEF)坐標和測向面的法向量，設第i個站的ECEF坐標為(xi,yi,zi)，測向面法向量為fi。

經緯高與ECEF坐標轉換公式如下：

(1)

式中：a為地球橢球的半長軸；b為半短軸；e為偏心率。

偵察站測向面法向量的計算公式為：

f=[sinBcosLsinφ-sinLcosφ,

sinBsinLsinφ+cosLcosφ,-cosBsinφ]T

(2)

然后，利用距離誤差與地球表面約束方程構造拉格朗日函數，求解定位點位置，此部分是算法的核心。

(3)

定位點的地球表面約束方程為：

(4)

利用式(3)和式(4)構造拉格朗日函數：

(5)

將式(5)表示為矩陣形式：

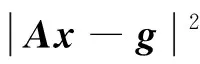
(6)

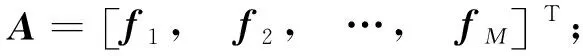
求解拉格朗日函數γ，可得：

(7)

由于地球長短半軸長度非常接近，因此矩陣B可以近似為單位陣，此時式(7)可以近似為：

(8)

忽略地球偏心率，式(4)可以近似為xTx=a2，將式(8)代入其中計算k值，可得：

(9)

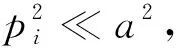
(10)

將式(8)和式(9)代入式(6)可得：

γ=xTATAx-xTATg-gTAx+gTg=

a2λi-2api

(11)

(12)

最后，計算定位點到偵察站的距離，距離較小者為正確定位點，并將其ECEF坐標轉換為經緯高，轉換公式如下：

(13)

2 仿真驗證

本節通過仿真實驗驗證算法在雙站和多站情形下以及有無測向誤差情況下的定位誤差。

(1) 無測向誤差

場景一：雙站測向交叉定位

兩站經緯度分別是(-1°，30°)和(1°，30°)，定位誤差如圖1所示。

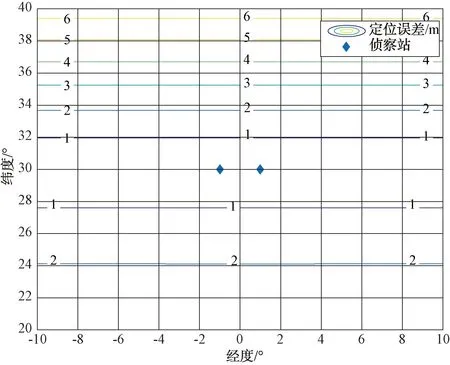
圖1 無測向誤差，雙站定位誤差分布圖

場景二：三站測向交叉定位

三站經緯度分別是(-1°，30°)、(1°，30°)和(0°，31.7°)，定位誤差如圖2所示。

(2) 有測向誤差，測向誤差的標準差為1°，誤差服從零均值正態分布

場景三：雙站測向交叉定位

兩站經緯度分別是(-1°，30°)和(1°，30°)，定位誤差如圖3所示。

場景四：三站測向交叉定位

三站經緯度分別是(-1°，30°)、(1°，30°)和(0°，31.7°)，定位誤差如圖4所示。

結論：算法適用于雙站和多站定位場景。當測向誤差為0時，算法對于1 000 km內目標的系統定位誤差在米級,遠小于測向誤差造成的定位誤差，基本可以忽略。

3 結束語

通過算法原理和仿真結果可知，本算法具有以下三方面優點：

從算法實現角度考慮，本算法的主要計算量是三階實對稱矩陣的特征分解，計算復雜度低，無需迭代，有解析解。

從算法誤差角度考慮，本算法對于1 000 km以內目標的系統定位誤差在米級，遠小于測向誤差造成的定位誤差，滿足實際需要。

從算法適用場景考慮，本算法適用于雙站和多站交叉定位場景。

綜上所述，本算法可以很好地應用于實際工程中。