基于改進粒子群算法的單目相機標定算法?
田少兵 范加利 王 正 段金升
(1.海軍航空大學(青島校區)艦面航空保障與場站管理系 青島 266041)(2.92941部隊 葫蘆島 125000)
1 引言
機器視覺作為實現智能制造的重要技術,近些年來獲得了快速的發展及廣泛應用,單目視覺測量技術是機器視覺的一個重要分支,是指將單目相機中獲取到目標圖像轉化為實際世界坐標系中的信息,常用于距離測量、目標定位等方面。相機標定是進行單目視覺測量和定位的先前步驟,是指利用優化方法獲取從圖像像素坐標系到三維世界坐標系的映射關系,相機標定精度往往影響視覺測量的準確度,因此研究如何準確地標定相機具有重要的意義。
文獻[1]提出了一種基于全參數自適應調節和變異機制的粒子群單目相機內參優化算法,分別給出了基于粒距的自適應學習因子調節策略和設計了基于粒子群平均粒距的自適應變異率,實驗結果表明,該方法具有較好的標定精度和收斂速度。文獻[2]提出了一種利用遺傳算法對相機內外參數進行優化求解的相機標定算法,將張正友標定法得到的參數作為初始值,通過遺傳算法對初始化參數迭代優化求解,實驗結果表明,改進后的標定算法提高了相機的標定精度。
本文提出了一種基于改進粒子群算法的相機標定算法,首先采用張正友相機標定法得到相機內參的初始值,再結合基于動態慣性權重系數的粒子群算法對得到的初始值進行迭代優化,得到最終的相機內參,實驗表明,本文算法優化后的相機內參準確性更高,算法收斂速度更快。
2 相機成像模型
相機模型成像始于三維世界,止于圖像像素點。相機成像模型是由像素坐標系、圖像坐標系、相機坐標系、世界坐標系等四個坐標系之間相互轉換建立的,具體是指圖像像素坐標點與三維世界空間點的一種映射關系[3~8]。

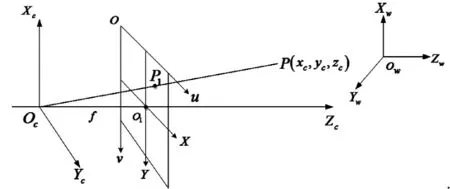
圖1 相機成像模型
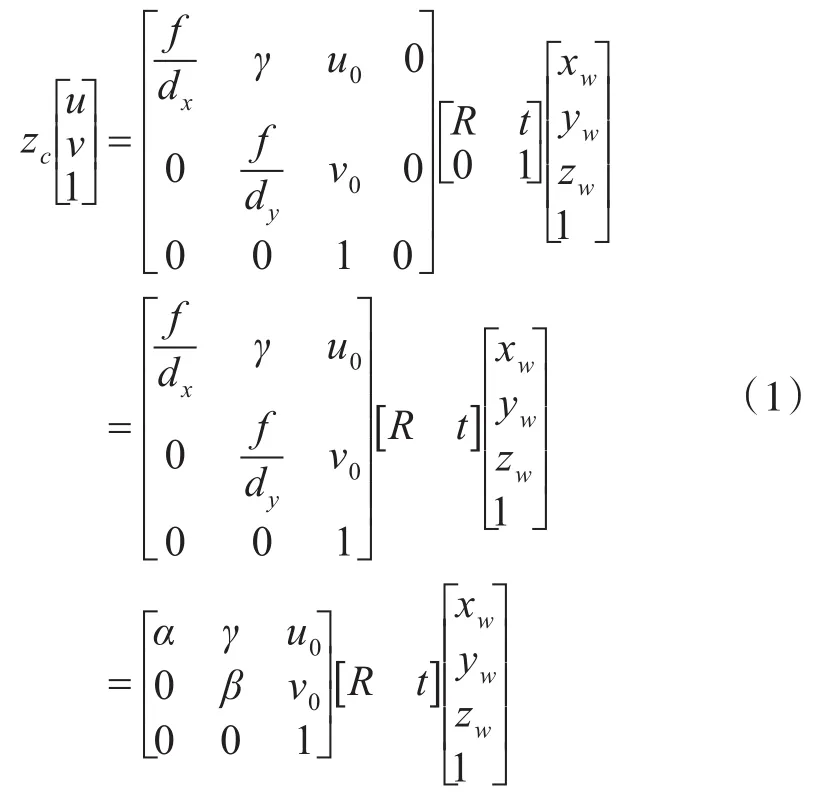
其中,(u0,v0)是像素坐標系中的原點,γ為傾斜因子,一般可取值為0。dx、dy分別表示像素在圖像坐標系x軸和 y軸方向上的物理尺寸,α=f/dx、β=f/dy分別表示像素坐標系中的u軸和v軸上的尺度因子,R和t分別表示相機外參的旋轉矩陣和平移矩陣。
上述的相機成像模型是在沒有受到外界干擾情況下的理想狀態的成像模型,實際當中,相機制造、安裝等過程中會造成各種各樣的誤差,導致相機通常會存在多種非線性畸變,為了使相機能夠獲得更加準確的標定結果,在相機標定時應該考慮加入相機的非線性畸變因素,以修正理想的相機成像模型。相機鏡頭畸變主要分為徑向畸變和切向畸變,則考慮加入徑向畸變和切向畸變的影響后的相機成像表達式為
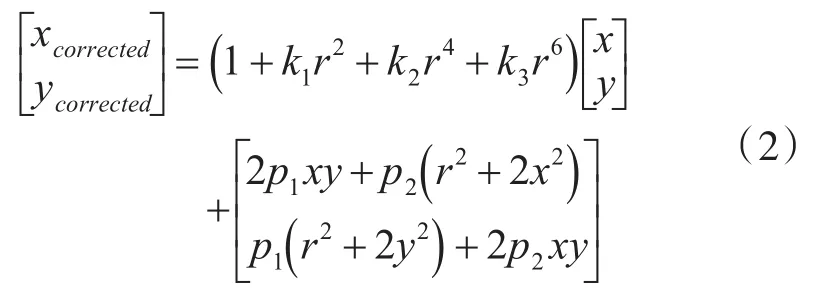
其中,(x,y)表示圖像畸變點的位置,(xcorrected,ycorrected)表示矯正后的新位置,式中r=x2+y2。k1、k2、k3為徑向畸變系數,p1、p2為切向畸變系數。
3 張正友相機標定法
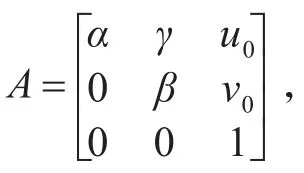

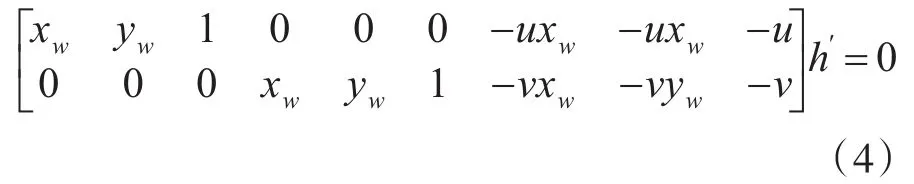
由于H中含有八個未知數,因此需要八個方程聯合對H矩陣進行求解[9]。棋盤標定板上面每個角點能提供兩個等式方程,則需要四個角點就可以計算圖像像素坐標系到世界坐標系的單應映射關系H。
由于式(3)中的單應性矩陣H是一個齊次矩陣,因此與真實的H之間相差一個比例因子λ,則有

其中r1、r2為單位正交向量,則有以下約束:

式6可進一步轉換為
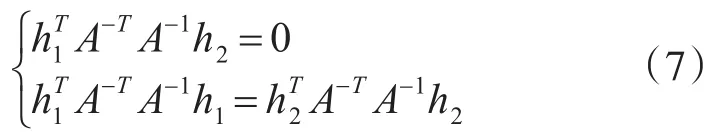
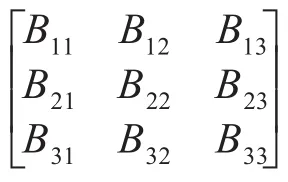

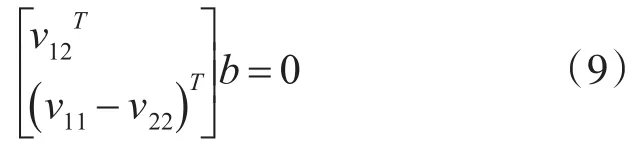
可利用最小二乘算法求解矩陣b,進而求解相機內參矩陣A的初始值。
4 改進粒子群算法的相機內參優化算法
粒子群算法(Particle Swarm Optimization,PSO)模擬鳥群隨機搜索食物的社會行為,其本質是一種全局搜索算法,對非線性、多目標等優化問題具有較強的全局搜索能力。PSO初始化為一群隨機粒子(隨機解),然后通過迭代找到最優解,在每次迭代期間,粒子通過跟蹤兩個“極值”來更新自身。一種稱為粒子個體極值,是自身找到的最優解,另一種稱為粒子全局極值,是全局粒子群的最優解[10~12]。
然而在上述過程中,如果某個粒子發現當前搜索區域的最優位置,則其他粒子會向這個位置快速靠攏,如果這個位置為局部最優解的位置,則迭代算法容易陷入早熟。在粒子群算法中,慣性權重是最重要的參數,增大其值可以提高算法的全局搜索能力,減小其值可以提高算法的局部搜索能力,因此設置合理的慣性權重,是避免陷入局部最優并高效的搜索的關鍵。
本文在原PSO算法的基礎上,根據算法運行時粒子目標值的分散程度來調整慣性權重,設置的動態慣性權重系數如式(10)所示
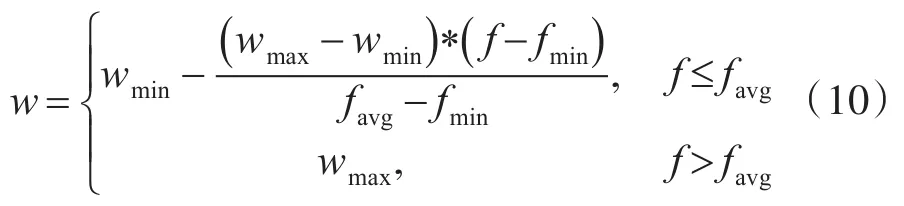
其中,f表示當前粒子實時的目標函數值,favg和fmin分別表示當前所有粒子目標函數值的平均值和最小值,最小慣性權重wmin設置為0.4,最大慣性權重wmax設置為1.0。
設置適應度函數如下:
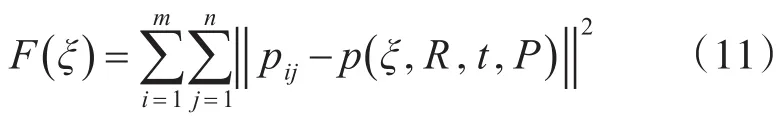
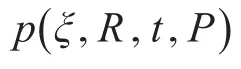
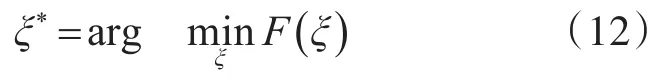
基于動態慣性權重系數的粒子群優化算法優化相機內參的總體步驟如下。
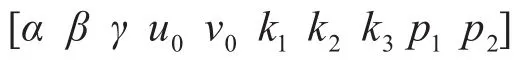
2)計算每個粒子的適應度值,并將每個粒子的當前位置作為個體最優位置,將其對應的適應度值作為當前粒子的個體最優值;對所有粒子的適應度值取最小值,作為全局最優值,并將其對應的粒子位置作為全局最優位置。
3)更新粒子的位置和速度:

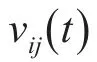
4)計算各粒子更新后的適應度值,并計算所有粒子的平均適應度值 favg,按照式(10)所示方法更新慣性權重w。
5)將每個粒子當前的適應度值與其個體最優值進行比較,若小于個體最優值,則將當前適應度值和對應的粒子位置作為該粒子更新后的個體最優值;計算所有粒子個體最優值的最小值,并與全局最優值進行比較,若小于全局最優值,則更新全局最優值。
6)判斷算法是否達到迭代完成條件,若未完成,返回執行步驟3),若完成,執行步驟7)。
7)算法執行結束,輸出結果。
5 實驗與分析
將棋盤標定板放置在平面上進行圖像采集,對采集到的棋盤標定圖像依次進行角點檢測、相機內參初始值計算、誤差分析等步驟。誤差分析是指利用計算出來的相機內參將實際世界平面坐標系中的坐標映射為棋盤上的角點像素坐標,然后與角點檢測算法檢測出的真實角點像素坐標求誤差。圖2展示了棋盤方格角點檢測的結果。

圖2 角點檢測結果
相機內參初始值確定之后,采用本文改進的粒子群算法對內參值進行優化,最終確定出準確的內參值。
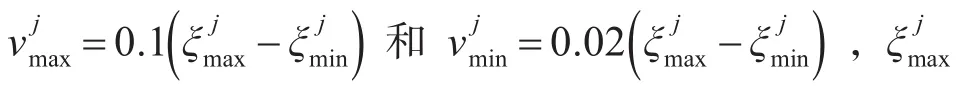

表1 粒子取值范圍
算法迭代500次之后,得到優化后的內參結果,分別與張正友相機標定法標定的投影誤差、原粒子群算法優化后的投影誤差進行比較。圖3為張正友標定算法的投影誤差,圖4為原粒子群算法優化后的投影誤差,圖5為本文改進粒子群算法優化后的投影誤差。
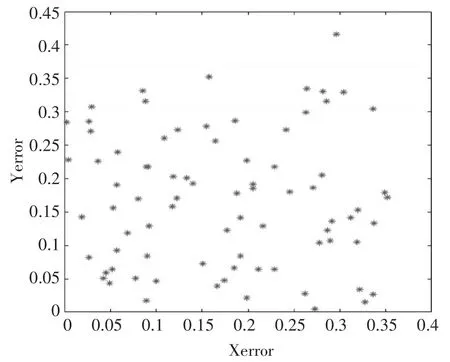
圖3 張正友相機標定法投影誤差

圖4 原粒子群算法優化后投影誤差

圖5 本文改進粒子群算法優化后投影誤差
結合圖3、4、5可知,相比于張正友相機標定法的投影誤差和原粒子群優化后的相機內參投影誤差,本文算法的投影誤差得到了很大的改善,表明本文算法的標定精度更高。
圖6和圖7分別反映了原粒子群算法迭代優化曲線和本文改進粒子群優化曲線,即適應度值隨著迭代次數變化的趨勢。

圖6 原粒子群算法迭代優化
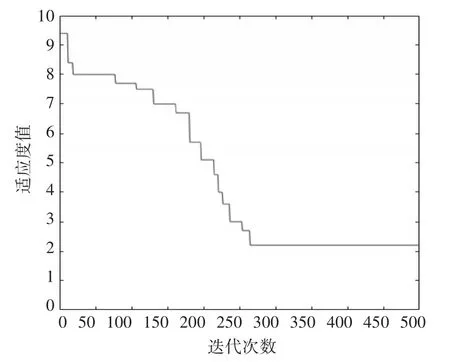
圖7 本文改進粒子群算法迭代優化
結合圖6、7可知,本文改進后的粒子群算法相對于原算法優化后的適應度值更低,比原算法的結果更優,同時,算法的收斂速度也更快。
6 結語
針對單目相機內參標定問題,本文在張正友相機標定算法計算出相機內參值的基礎上,加入基于動態慣性權重系數的粒子群優化算法進行進一步優化。實驗結果表明,本文提出的算法標定準確度更高,算法進行優化時收斂速度更快,有效地克服了陷入局部最優解的問題。

