擴大斜切式緩沖結構對時速400 km鐵路隧道口微氣壓波緩解研究

王田天，胡 沖，龔彥峰，楊明智，熊小慧，蹤敬良，陸意斌，*

(1. 中南大學 交通運輸工程學院，軌道交通安全教育部重點實驗室，長沙 410075；2. 湖南大學 機械與運載工程學院，長沙 410082；3. 中鐵第四勘察設計院集團有限公司，武漢 430063；4. 水下隧道技術國家地方聯合工程研究中心，武漢 430063)

0 引言

隨著高速鐵路的不斷發展，中國高鐵的最高運營速度已達350 km/h，但由于旅客出行需求和列車運行能力的矛盾依然突出，國家已開始研發設計時速400 km的高速列車。由于我國地形復雜，山地占國土面積的2/3，在高速鐵路建設的過程中需修建大量鐵路隧道，而車速的提高不可避免地會加劇車-隧耦合氣動效應[1-2]。如圖1所示，高速列車鼻尖進入隧道的瞬間，會在車前產生初始壓縮波，該壓縮波以聲速沿著隧道長度方向傳播并不斷激化，到達出口時會以脈沖形式從隧道出口向外輻射，形成脈沖狀的壓力波，稱之為隧道口微氣壓波或簡稱為微氣壓波[3-5]。微氣壓波幅值隨著列車速度的增加而顯著增大，當列車以時速小于250 km通過短隧道時，微氣壓波幅值基本與列車速度的三次方成正比[6]；而隨著車速和隧道長度的增加，微氣壓波幅值可與3倍以上的車速成正比[7]。過大的脈沖狀壓力不僅對隧道口附近的環境產生不利的影響，同時也會嚴重影響附近居民的正常生活[8-9]。因此，有效緩解時速400 km高速鐵路隧道口微氣壓波對于鐵路隧道的建設以及保障隧道口周圍環境和居民安全具有重要的意義。

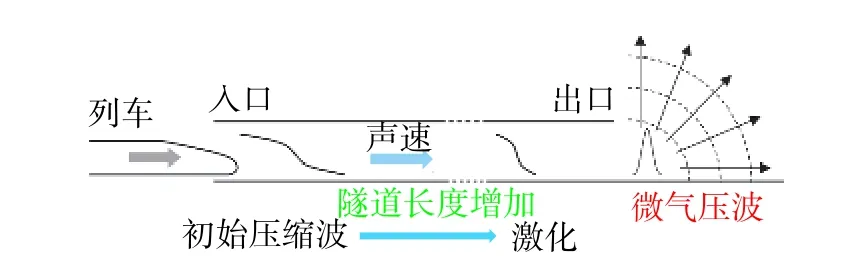
圖1 微氣壓波產生示意圖Fig. 1 Schematic diagram of the generation of the micro-pressure wave

在近幾十年間，國內外對緩解微氣壓波的方法進行了大量研究。降低微氣壓波的基本思路是在壓縮波形成和傳播階段減小其壓力梯度，現有的緩解方法主要分為兩類，一是改變隧道結構（比如在隧道口加設緩沖結構或增大隧道斷面面積或修建輔助坑道等）[6]；二是改變列車頭部形狀（增加列車頭部流線型長度和改變列車斷面面積），從而達到減小初始壓縮波最大壓力梯度的效果[10]。Yamamoto[11]構建了一個稱為“輻射立體角模型”（RSA模型）的預測模型，利用隧道出口周圍的立體角來預測地形對微氣壓波的影響，后來Miyachi[12]擴展了山本的RSA模型，生成了微氣壓波的聲學模型，該模型同時考慮了二階聲源和隧道口周圍地形的聲學效應。Nagai[13]和Sanetoshi[14]通過數值模擬和動模型試驗研究了緩沖結構形式以及優化緩沖結構斷面對壓力梯度的影響，結果發現優化后能顯著降低初始壓縮波的壓力梯度。賀旭洲等[15]利用數值模擬對斜切式洞門緩沖結構開口率進行了優化分析，并給出了不同車速下的最優開口率。Zhang等[16]使用1/20比例的動模型試驗研究了傾斜的隧道口對微氣壓波的影響。Wang等[17]研究了改變隧道斷面參數對壓力波動的影響。此外，有學者對緩沖結構緩解微氣壓波的機理進行研究。周丹[18]認為等截面擴大段緩沖結構使列車前空氣在進入隧道前提前被壓縮，從而增大了壓力上升到最大值的時間；且緩沖結構將壓力上升分為了兩個或三個階段，從而壓力梯度峰值得到減小。鄭長青[19]和牛紀強[20]等認為開口式緩沖結構對初始壓縮波幅值基本沒有緩解效果，但是可以增加壓力上升的時間，從而降低壓力梯度達到緩解微氣壓波的效果。

近幾年開始有學者對更高速度下列車隧道空氣動力學問題進行研究。吳劍等[21]開展了時速 300 km至350 km高速鐵路雙線隧道微氣壓波激化作用及緩解措施研究。范勝利等[22]研究了一種帶有排氣管的擴大等截面式的新型緩沖結構，且給出了排氣管的參數限制，認為排氣管的長度應小于壓縮波前長度的一半；單個排氣管的斷面積不宜超過緩沖結構斷面面積的20%；并可以針對不同的車速調節排氣管的長度或改變排氣開孔的位置或數量以達到有效減緩微氣壓波的目的，但此新型緩沖結構是在車速360 km/h下進行的研究，其對更高車速下微氣壓波的緩解效果的普適性需進行深入研究，而本研究車速為400 km/h，且緩沖結構帶有斜切和開孔，氣動效應也更為復雜。魏雨生等[23]對高速列車以時速400 km通過隧道時的列車和隧道壓力變化進行了數值模擬，發現車體表面和隧道壁面最大壓力變化幅值比300 km時分別提升了90.4%和65.3%，但未對隧道口的微氣壓波進行研究。

綜上，目前國內外針對高速列車以時速400 km通過隧道時的微氣壓波的緩解方法研究較少，存在較大空缺。故本文以時速400 km高速列車經過隧道引發的微氣壓波問題為導向，對隧道長度、緩沖結構長度和緩沖結構開孔個數等多個參數展開耦合研究，以期為緩解時速400 km高速鐵路隧道口微氣壓波的緩沖結構設計提供參考。

1 數值計算方法

1.1 數值計算模型

高速列車模型如圖2所示，由于微氣壓波主要與車頭的形狀相關，故選用2車編組（頭車 + 尾車）的復興號高速列車組（型號：復興號400-AF）為研究對象，同時對轉向架、受電弓、門窗等基本不影響計算準確性的結構進行簡化，保留列車的典型氣動外形。我國現有運營速度350 km/h的高速列車，主要在京滬、京張等線路上運行，其隧道選用斷面積為100 m2的典型高鐵雙線隧道，兩列車的線間距為5 m[24]，如圖3所示。本文選取此隧道斷面進行研究。由于相關研究表明緩沖結構斜切角為30°、擴大段面積與隧道斷面積比約為2∶1時，對微氣壓波有較好的緩解效果[16]。故本文選取了斜切角為30°的等截面擴大段（擴大段面積S擴= 200 m2）的緩沖結構為研究對象，分析其長度和開孔率對時速400 km高速鐵路隧道口微氣壓波的緩解效果。如圖4所示，緩沖結構斜切部分的長度為22.56 m，有研究表明列車以一定速度通過隧道，當等截面緩沖結構的長度超過4倍的隧道等效水力直徑時，微氣壓波幅值不再隨緩沖結構長度的增加而變化[18]。本文模型隧道的等效水力直徑為11.6 m，且緩沖結構帶有斜切和開孔，列車速度更高，所以本研究緩沖結構的總長度L在本研究中設置4種，分別為68.56 m、78.56 m、88.56 m和98.56 m；每個開孔的面積為6 m × 4 m，兩孔間間隔均為4 m，不同開孔數的工況設置為：1個開孔時為序號①開孔，2個開孔時為①②開孔，3個開孔時為①②③開孔，4個開孔時為①②③④開孔，5開孔時為①②③④⑤開孔。

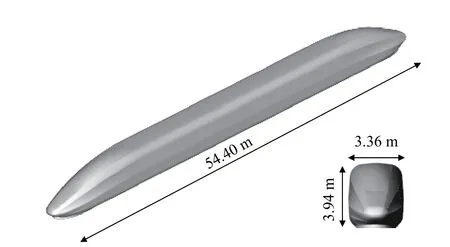
圖2 兩車編組高速列車模型Fig. 2 High-speed train model of a two-car marshalling

圖3 100 m2雙線隧道斷面Fig. 3 Cross-section of a 100 m2 double-track tunnel

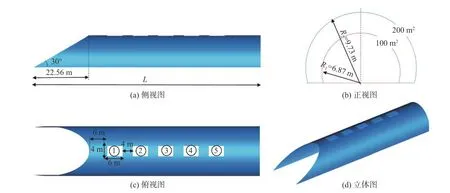
圖4 研究緩沖結構長度和開孔個數影響時所采用的幾何模型（S隧 = 100 m2，S擴 = 200 m2）Fig. 4 Geometric model used to study the influence of the tunnel-hood length and the number of opening holes (S隧 = 100 m2，S擴 = 200 m2)

1.2 計算區域和邊界條件

計算區域如圖5所示，分為靜止區域和滑移區域2個部分，靜止區域又包含列車進口大氣區域、隧道（長度L0因工況而定）和列車出口大氣區域。考慮到流場和尾流擾動的充分發展，從隧道的兩端分別向兩側各延伸450 m。計算域中列車進口大氣區域的地面和與隧道接觸的面定義為無滑移壁面，其他邊界定義為壓力出口；在列車出口大氣區域中，地面和與隧道接觸的面定義為無滑移壁面，其余邊界均設置為壓力遠場邊界；隧道和列車均設置為壁面邊界條件[25]；包含列車的滑移區域的兩端分別定義為壓力入口和壓力出口邊界，且在滑移區域和靜止區域之間設置交換面以實現數據交換。另外，值得注意的是，由于本文中的流動為三維可壓縮氣體的不等熵流動，故所有壁面邊界條件均為絕熱壁面，所有邊界初始溫度均設置為300 K。

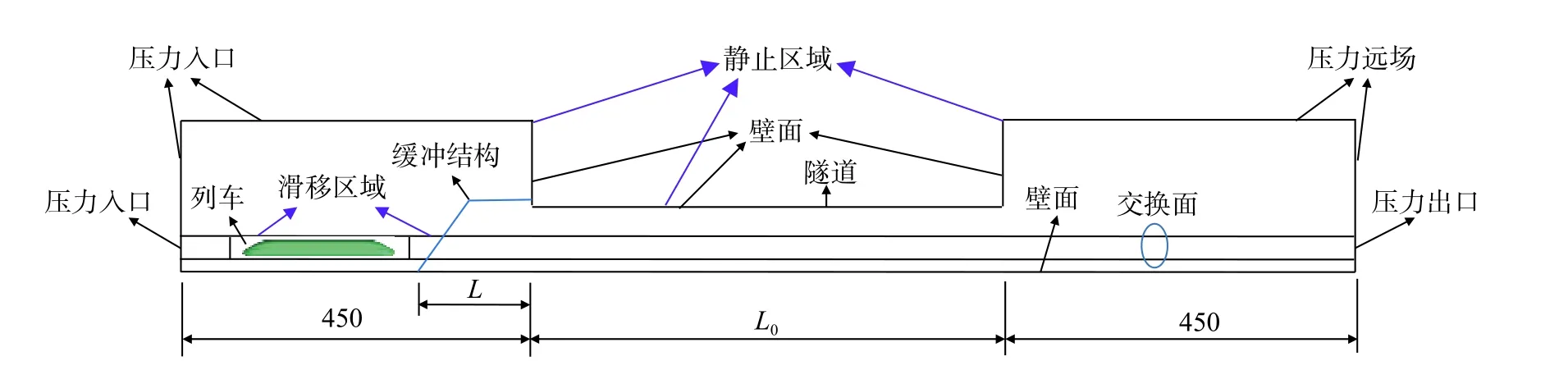
圖5 計算區域和邊界條件(單位：m)Fig. 5 Computational domain and boundary conditions (unit: m)

1.3 網格劃分

如圖6所示，本研究采用的高速列車外形復雜，且在隧道口設置了帶斜切的緩沖結構，因此選擇混合網格對計算域進行離散。列車周圍區域及斜切緩沖結構的部分區域離散為非結構化網格，其余部分離散為結構化網格，列車表面上的最小網格尺寸為0.05 m，隧道表面最小網格尺寸為0.15 m。為了對網格的無關性進行檢驗，按上述的方法調整網格參數，將下文2.1節中的動模型試驗的列車和隧道劃分為粗、中、細三種網格（其中中網格劃分策略與本文選用的網格劃分策略一致），網格單元總數分別為4.32×106、9.74×106、1.728×107。選取列車中部測點和隧道中部測點的壓力峰-峰值與實驗結果進行比較，三種網格的網格密度和壓力峰-峰值的偏差結果列于表1。由表1可知，粗網格計算得到的列車表面和隧道壁面的壓力峰-峰值較實驗的偏差分別為?2.9%和?3.6%，而中等數量網格的列車和隧道的偏差分別為1.2%和?1.6%，細網格的偏差與中等網格基本一致，可以看出粗網格計算的結果與對比實驗偏差較大。進一步細分網格，當網格數量超過9.74×106時，計算結果隨網格數量增加變化較小，證明網格已經收斂，同時說明9.74×106的中等數量的網格可以同時滿足計算精度和計算效率兩方面的要求，所以本文選取中等網格劃分策略進行研究。

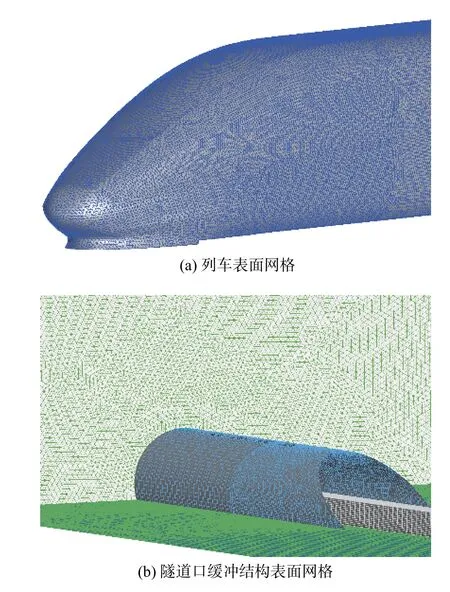
圖6 計算網格分布Fig. 6 Computational grid distribution

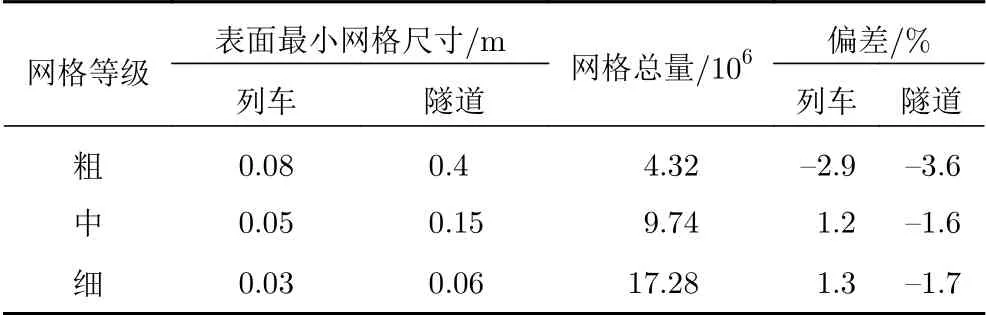
表1 網格密度及峰-峰值的偏差Table 1 Grid density and the peak-to-peak value deviation

1.4 計算方法及求解設置

本研究選用的求解軟件為基于有限體積法的ANSYS FLUENT求解器。高速列車通過隧道時，由于空氣受到隧道和車體壁面的束縛，需考慮空氣的壓縮性[26-27]。因此，本文選用基于可壓縮 N-S方程的RNGk-ε湍流模型，并采用滑移網格技術，對高速列車通過隧道時的復雜空氣流場進行求解[28-29]。速度和壓力的耦合方式選用SIMPLE 算法，基于格林高斯的單元法來控制梯度變化，時間離散采用二階隱式格式，空間離散采用二階迎風格式[10]。時間步長設置為0.0075 s，并設置50次內部迭代[16]。

1.5 測點布置

因我國對微氣壓波的評判標準為：距隧道口20 m處的微氣壓波要小于50 Pa，距隧道口50 m處的微氣壓波要小于20 Pa[30]。故隧道口微氣壓波測點分布如圖7所示，在距離隧道口20 m、50 m的隧道中線兩側分別對稱布置2個測點，靠近列車一側的測點編號為1和2，遠離車一側的測點編號為3和4，所有測點距離軌面高為1 m。

圖7 微氣壓波測點的布置Fig. 7 Layout of the micro-pressure wave measurement points

2 數值方法驗證

2.1 動模型實驗

本次動模型試驗在中南大學軌道交通安全教育部重點試驗室的動模型試驗平臺進行，該平臺可用于單軌試驗和雙軌試驗，主要由三部分組成，分別用于加速、測試和制動[31]。該平臺擁有先進的列車穿越隧道和列車交會實驗模擬研究系統，并獲得CNAS國際認證（注冊號CNAS L 10220）和CMA中國國家檢測資質認證（證書號170021002479），能夠對本文所采用的數值計算方法進行可靠性評價。

如圖8，動模型試驗采用1∶20縮比模型，列車模型長度為2585 mm，高度為194.5 mm，寬度為163.3 mm；隧道模型對應的實際凈空面積為100 m2，長164 m，線間距0.25 m。本次動模型試驗的速度為400 km/h，在此平臺上一共進行了15次彈射，其中發射速度不在目標速度1%以內的工況不被選用。為記錄列車過隧道的產生的壓力變化，如圖9，在隧道壁面上布置5個測點分別記為S1-S5，其中S3為靠近列車一側的測點；列車表面布置5個測點，記為T1-T5，如圖10。

圖8 動模型試驗平臺Fig. 8 Moving model test platform

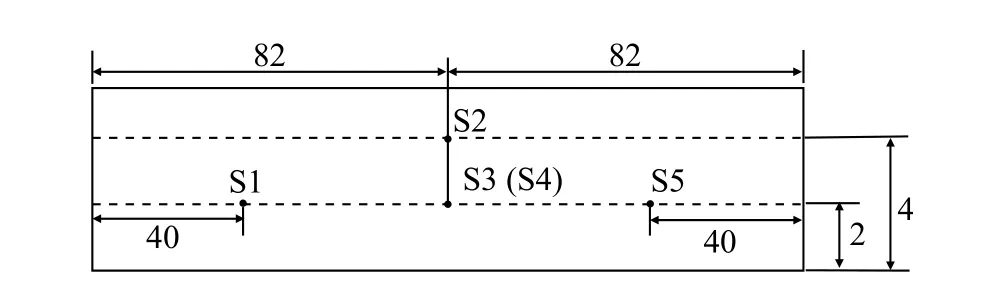
圖9 隧道壁面測點(單位：m)Fig. 9 Measurement points on the tunnel surface (unit: m)

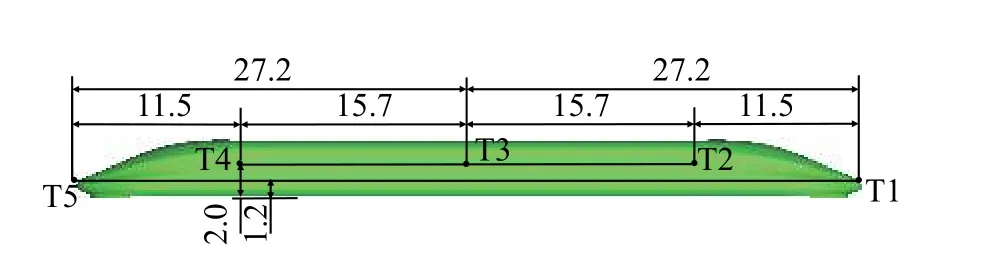
圖10 列車表面測點(單位：m)Fig. 10 Measurement points on the train surface (unit: m)

2.2 結果分析對比

按照上文的數值方法對試驗模型進行網格劃分和模擬計算。由于動模型試驗采用的是1∶20的比例，所以試驗時間要進行相應轉換，同時由于雷諾數大于3.6×105，模型尺寸對列車周圍的流場影響很小，因此試驗測點的壓力值可以代表全尺寸模型的壓力值[32]。圖11（a）和圖11（b）分別為隧道壁面測點S3和列車表面測點T1的壓力時程曲線，發現與動模型試驗相比，兩測點的壓力峰-峰值的偏差分別為?1.4% 和1.1%，證明本文的數值方法能夠正確反映壓力極值的變化規律。圖11（c）為圖11（a）中隧道壁面測點初始壓縮波的壓力梯度時程曲線，可以看出數值模擬和動模型試驗的初始壓縮波梯度曲線吻合較好，且兩者壓力梯度最大值的偏差僅為1.2%。由式（1）可知微氣壓波的壓力幅值Δpw與初始壓縮波的最大壓力梯度成正比[1]，所以可以得出數值模擬與動模型試驗的微氣壓波幅值的偏差也為1.2%，這證明本文采用的數值方法具有較高的精度。

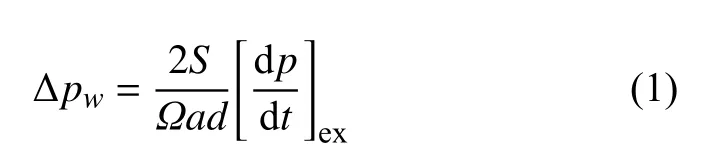
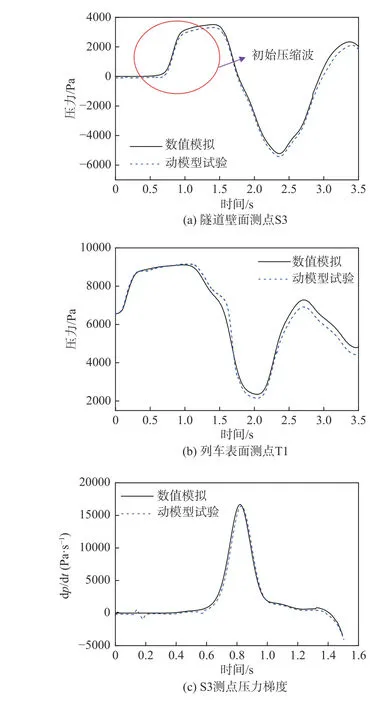
圖11 動模型實驗和數值模擬所得壓力時程曲線對比Fig. 11 Pressure time history comparison between the moving model test and the numerical simulation

3 計算結果和討論

3.1 無緩沖結構的隧道長度對微氣壓波的影響

截至2020年底，中國已投入運營的高速鐵路隧道共3631座，總長約 6003 km，其中10 km以上的特長隧道只有87座[33]，且趙勇等2017的調查結果顯示中國高速鐵路隧道長度在3 km以下的數量占高速鐵路隧道總數的80%以上[34]。可見我國高速鐵路隧道絕大多數都在3 km以內，5 km以上的隧道大部分位于群山峻嶺，且對應的列車設計時速較小。因此本文選取1 km、2 km和5 km的隧道長度進行研究。

圖12為時速400 km高速列車通過長度1 km隧道時，距隧道口20 m處同一截面上對稱的兩個測點（測點1和測點3）和距隧道口50 m處截面上對稱的兩個測點（測點2和測點4）的微氣壓波曲線圖，可以發現同一截面上對稱的兩測點曲線基本吻合，這說明微氣壓波在同一截面上相同高度的強度相同。所以本文選取靠近列車一側的測點1（距隧道口20 m）和測點2（距隧道口50 m）進行分析。

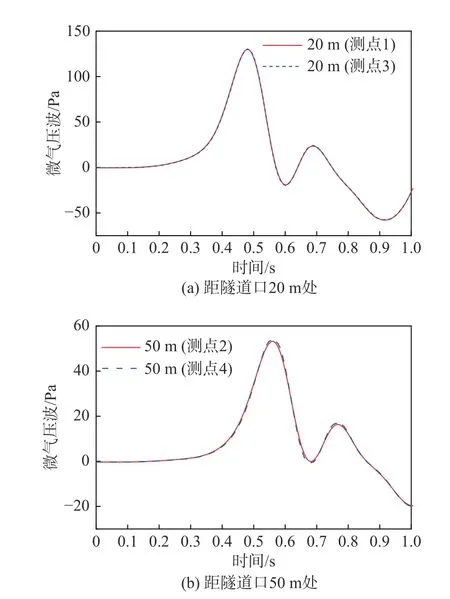
圖12 隧道口微氣壓波曲線圖Fig. 12 Micro-pressure wave curves at the tunnel exit

圖13（a、b）為高速列車以時速400 km通過長度（L0）為1 km、2 km、5 km的無緩沖結構隧道時，測點1和測點2的微氣壓波隨時間變化的曲線圖。可以發現隧道長度在5 km以內時，微氣壓波幅值隨著隧道長度的增加而增大，這是因為初始壓縮波在隧道內傳播時，由于擠壓和摩擦效應，空氣密度和溫度隨之增加，引起聲速的提高，使初始壓縮波后部比前端傳播的更快進而使其激化所導致。

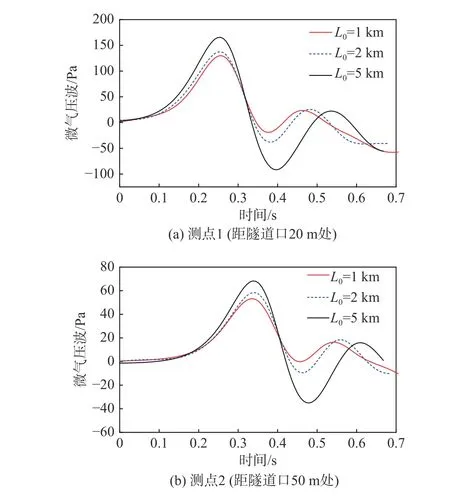
圖13 不同隧道長度下微氣壓波曲線圖Fig. 13 Micro-pressure wave curves for different tunnel lengths

表2和表3分別為高速列車通過不同長度隧道時，測點1和測點2的微氣壓波幅值及相對1 km隧道的增長率。可以發現，在每個測點隧道長5 km的微氣壓波幅值及相對隧道長1 km的增長率都為最大，測點1和測點2微氣壓波幅值分別為165.7 Pa和68.3 Pa，微氣壓波幅值最大增長率分別為27.4%和28.4%，均超過國家相關標準。故下文開展斜切（30°）等截面擴大段式緩沖結構對微氣壓波的緩解研究，分析其長度和開孔數對微氣壓波的影響。

表2 不同隧道長度下測點1微氣壓波幅值及增長率Table 2 Amplitude and growth rate of the micro-pressure wave at measurement point 1 for different tunnel lengths

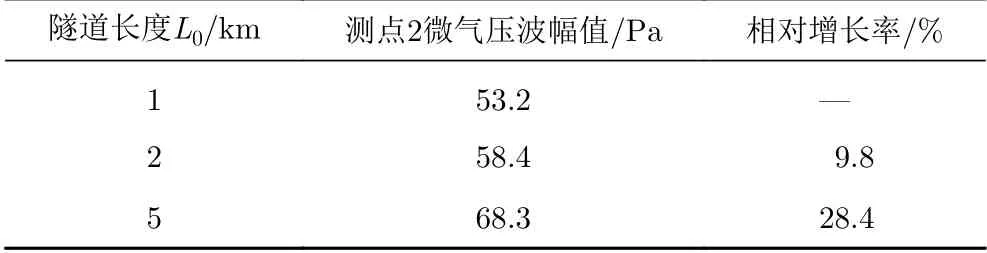
表3 不同隧道長度下測點2微氣壓波幅值及相對增長率Table 3 Amplitude and growth rate of the micro-pressure wave at measurement point 2 for different tunnel lengths

3.2 帶斜切（30°）的緩沖結構長度對微氣壓波的影響

圖14（a、b）為高速列車以時速400 km/h通過不同長度的緩沖結構隧道（隧道長1 km）時，測點1和測點2的微氣壓波隨時間的變化曲線，其中緩沖結構長度L分別為68.56 m、78.56 m、88.56 m、98.56 m，且選用無緩沖結構的工況作為對比。可以發現與無緩沖結構相比，每個長度的緩沖結構對微氣壓波都有較好的緩解效果，最優緩沖結構長度為88.56 m。表4和表5分別為測點1和測點2在不同長度緩沖結構下微氣壓波幅值及其相對無緩沖結構的緩解率，可見緩沖結構長88.56 m時，測點1和測點2的微氣壓波幅值的最大緩解率分別為59.2%和56.0%。圖15為兩個測點微氣壓波幅值隨緩沖結構長度變化的曲線，可以看出微氣壓波幅值隨著緩沖結構長度的增加先減小后又略微增大。

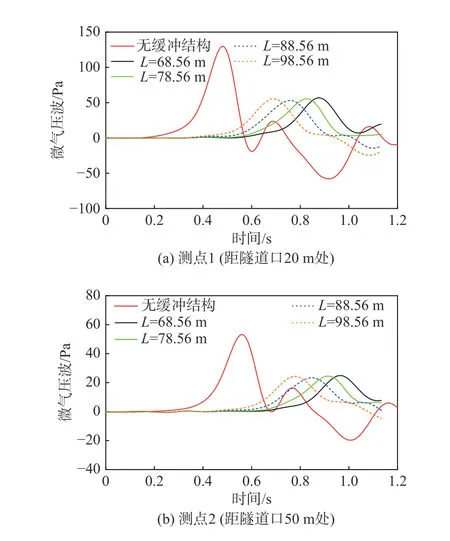
圖14 不同緩沖結構長度下隧道口微氣壓波曲線圖Fig. 14 Micro-pressure wave curves at the tunnel exit for different tunnel-hood lengths

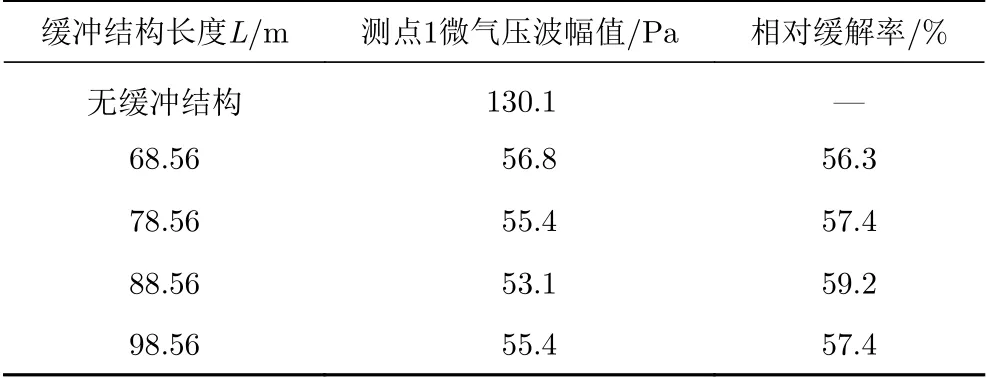
表4 不同緩沖結構長度下測點1微氣壓波幅值及相對緩解率Table 4 Amplitude and alleviative rate of the micro-pressure wave at measurement point 1 for different tunnel-hood lengths

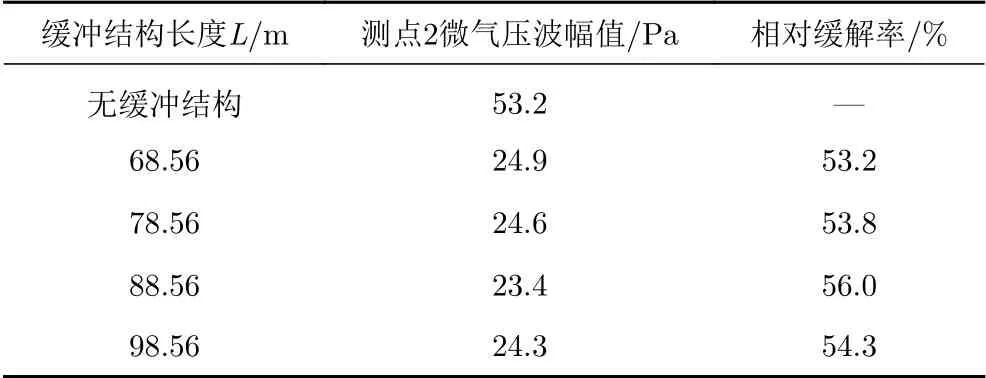
表5 不同緩沖結構長度下測點2微氣壓波幅值及相對緩解率Table 5 Amplitude and alleviative rate of the micro-pressure wave at measurement point 2 for different tunnel-hood lengths

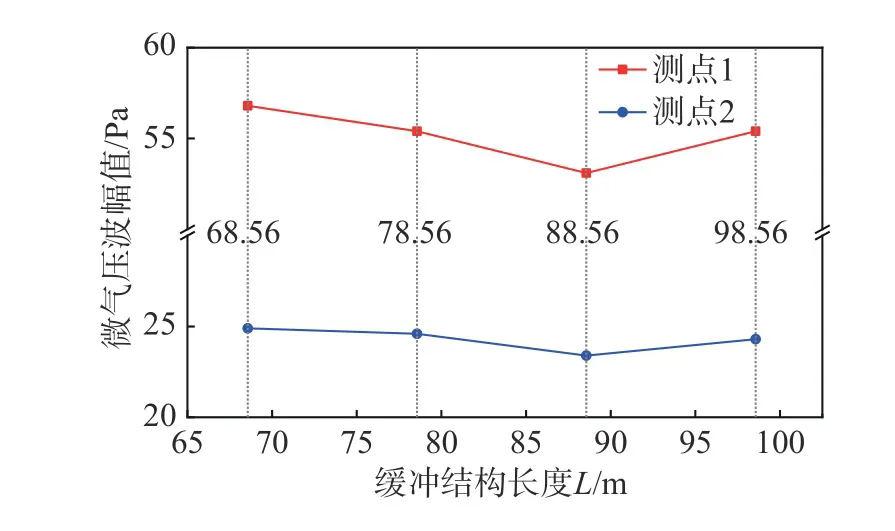
圖15 微氣壓波幅值隨緩沖結構長度的變化Fig. 15 Variation of the amplitude of the micro-pressure wave with the tunnel-hood length

分析其原因，在周丹[18]的研究中可知：當緩沖結構長度在一定倍數的隧道等效水力直徑之內時，微氣壓波幅值隨緩沖結構長度的增加而減小；當其長度超過一定倍數的隧道等效水力直徑后，微氣壓波基本不變，此長度定為臨界長度Lh。其研究也發現了不同的車速對應不同的Lh，當緩沖結構長度超過各自速度對應的Lh時，速度越大，在該長度之后對應的微氣壓波增大的越明顯，這與本文結果相符。在最優長度的緩沖結構下（88.56 m），測點1和測點2的微氣壓波幅值分別為53.1 Pa和23.4 Pa，仍不滿足國家標準，故需進一步對微氣壓波進行緩解。

3.3 緩沖結構開孔個數對微氣壓波的影響

由上文知隧道長1 km時，不開口緩沖結構長為88.56 m對微氣壓波緩解效果最好，但仍不能達到標準要求，所以下文研究隧道長1 km時，斜切（30°）緩沖結構（L= 88.56 m）的開孔率對微氣壓波的影響，以尋求更好的緩解效果。

圖16為高速列車以時速400 km通過不同開孔數的緩沖結構隧道時，測點1和測點2的微氣壓波隨時間的變化曲線，可以發現相對于0開孔的緩沖結構，開1孔和開2孔可以使微氣壓波幅值減小，開3、4、5孔會使微氣壓波幅值增大，且微氣壓波曲線中的第一個峰值隨著開孔數的增加向后移動。這是因為開孔的位置是沿著列車運行方向縱向排列的，隨著列車的運行，開孔處發生泄氣，延長了初始壓縮波形成的時間，從而引起微氣壓波達到幅值的滯后。

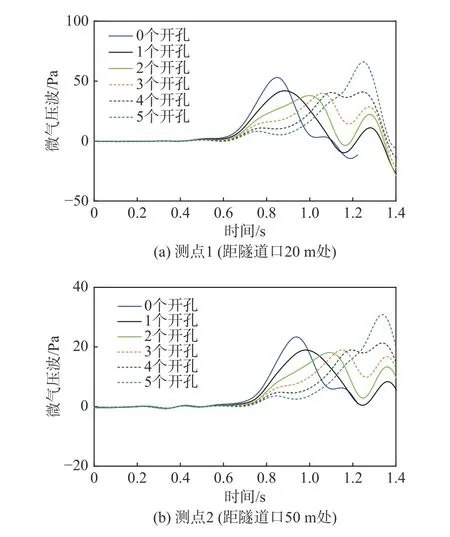
圖16 不同開口數的緩沖結構下微氣壓波曲線圖Fig. 16 Micro-pressure wave curves for tunnel-hoods with different numbers of opening holes

表6和表7分別為測點1和測點2在不同開孔數的緩沖結構下微氣壓波幅值和相對無緩沖結構的緩解率。可見測點1和測點2具有相同的變化規律：微氣壓波幅值隨開孔數的增加先減小后增大，在開孔數為2時微氣壓波幅值最小，這與Liu[35]等發現的“微氣壓波幅值隨緩沖結構開孔率的增加先減小后增大”的規律基本相符，但其研究的最優開孔率為0.018，本文兩個開孔對應的開孔率為0.0213，這主要是因為本研究的車速為400 km/h，緩沖結構帶有斜切，且緩沖結構長度面積、隧道長度面積等都與文獻[35]研究的不同，但整體變化規律是一致的。下面分析此變化規律的原因：孔①②③④⑤沿緩沖結構長度方向縱向排列，當開孔數較少時（2個開孔以內），列車進入緩沖結構被壓縮的空氣會在開孔處發生泄氣，延長了初始壓縮波最大值形成的時間，從而初始壓縮波的最大壓力梯度下降，且2個開孔時泄氣量大于1個開孔，所以2開孔的初始壓縮波最大壓力梯度小于1開孔；當開孔數大于2時，因為①②開孔已經分散了大部分壓縮氣體，隨著列車的運動，在開孔處會有進氣和出氣的復合作用，且在開孔處和擴大段與隧道交接處產生的復雜小波會相互疊加，在上述因素的共同作用下，相對于2開孔時，初始壓縮波的最大壓力梯度會增大。測點1和測點2微氣壓波幅值分別為37.9 Pa和18.1 Pa，相對無緩沖結構時的緩解率分別為70.9%和66.0%，都已滿足標準要求。

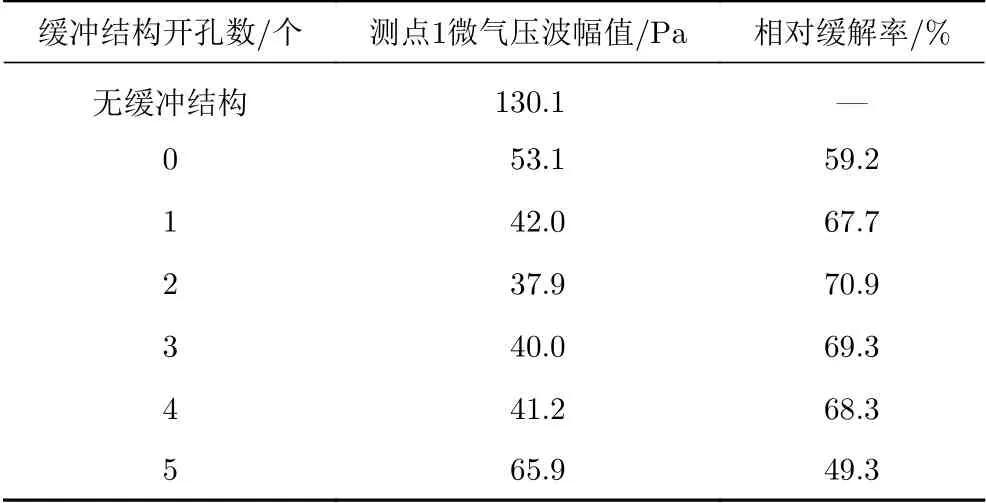
表6 不同開孔數的緩沖結構下測點1微氣壓波幅值及相對緩解率Table 6 Amplitude and alleviative rate of the micro-pressure wave at measurement point 1 for tunnel-hoods with different number of opening holes

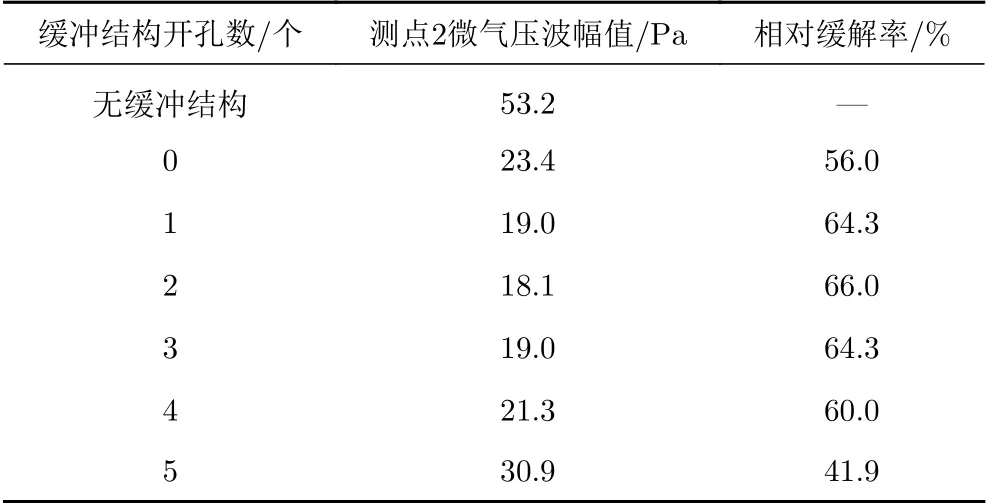
表7 不同開孔數的緩沖結構下測點2微氣壓波幅值及相對緩解率Table 7 Amplitude and alleviative rate of the micro-pressure wave at measurement point 2 for tunnel-hoods with different numbers of opening holes

圖17（a）為采用斜切30°長88.56 m開2孔的等截面擴大段緩沖結構，隧道長分別為1 km、2 km、5 km時壓縮波變化的曲線，圖17（b）為對應壓力梯度的變化。可以看出，壓力幅值和壓力梯度的幅值都受到了隧道在長度方向的激化，隨隧道長度的增加而增加，這與3.1節中得到的微氣壓波受隧道長度的激化的規律一致。另外，Yamamoto[36]利用遠場和低頻的近似方法得到了微氣壓波幅值與壓縮波的最大壓力梯度成正比的關系，所以微氣壓波幅值與壓力梯度幅值變化規律具有一致性。同時，本文旨在研究400 km時速下的隧道口微氣壓波的緩解措施，以使微氣壓波達到相關標準，所以直接監測隧道口的微氣壓波是可取的。

圖17 不同隧道長度下壓縮波及壓力梯度的變化Fig. 17 Variation of the compression wave and pressure gradient for different tunnel lengths

圖18為隧道長1 km、2 km、5 km時，采用斜切30°長88.56 m開2孔的等截面擴大段緩沖結構，在測點1和測點2的微氣壓波幅值的曲線，表8是對應的微氣壓波幅值。可見采用上述緩沖結構可將長1 km、2 km、5 km隧道的微氣壓波幅值都降到標準以下。故本文提出的斜切角為30°、擴大段長度為88.56 m、開2孔的緩沖結構能使長為5 km及以下長度的時速400 km高速鐵路隧道口微氣壓波緩解達到國家相關標準。

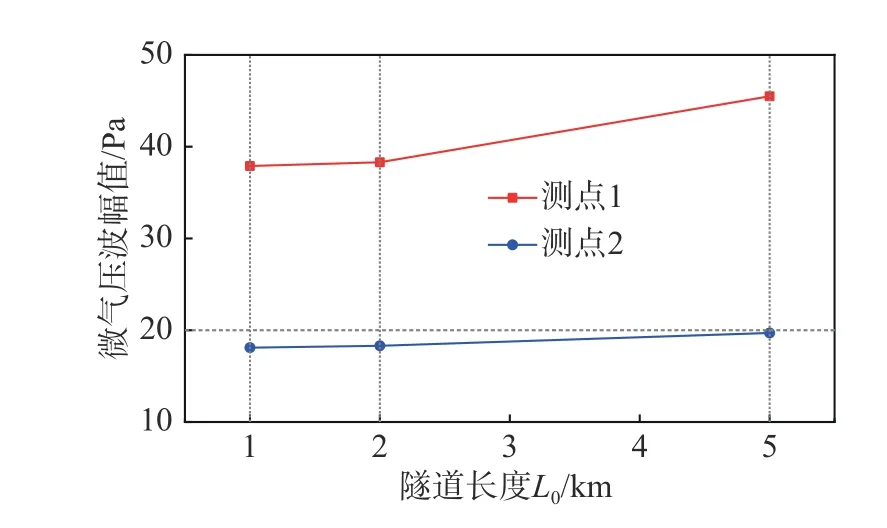
圖18 緩沖結構開2孔時微氣壓波幅值隨隧道長度的變化Fig. 18 Variation of the amplitude of the micro-pressure wave with the tunnel length for the tunnel-hood with 2 opening holes

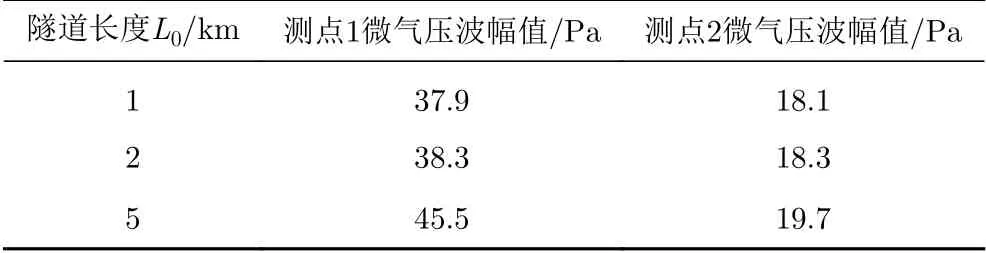
表8 緩沖結構開2孔時不同隧道長度的微氣壓波幅值Table 8 Amplitude of the micro-pressure wave for different tunnel lengths with 2 opening holes on the tunnel-hood

4 結論

本文通過數值模擬和動模型實驗，對時速400 km高速鐵路隧道口微氣壓波進行分析，研究隧道長度、斜切角為30°的緩沖結構長度和開孔數對微氣壓波的影響。主要結論如下：

1）隧道長度在5 km以內時，微氣壓波幅值隨著隧道長度的增加而增大，其中隧道長5 km與1 km相比，在距隧道口20 m和50 m處微氣壓波幅值分別增大了27.4%和28.4%；

2）微氣壓波幅值隨著緩沖結構長度的增加先減小后又增大，隨著緩沖結構開孔數的增加微氣壓波幅值先減小后增大，存在最優的緩沖結構長度和開孔數，最優長度為88.56 m，最優開孔數為2開孔；

3）最優長度與最優開孔數組合的緩沖結構，能使隧道長為1 km的微氣壓波幅值在距隧道口20 m和50 m處分別緩解70.9%和66.0%；并能使長為5 km及以下長度的時速400 km高速鐵路隧道口微氣壓波緩解達到國家相關標準。