一種仿蝗蟲腿空間緩沖吸附機構緩沖參數研究

李 龍，葛澤宇，田應仲，張 泉

(1. 上海大學機電工程與自動化學院，上海 201900；2. 上海市智能制造及機器人重點實驗室，上海 201900；3. 上海大學人工智能研究院，上海 201900)

0 引 言

隨著人類對太空探索的逐步深入，大量航天器被送入太空軌道。當這些航天器由于各種復雜的原因發生故障或損壞時，需要利用小型的緩沖器附著在航天器的表面對其進行故障診斷、故障維修、故障監控或通信檢查等。高速運動的小型緩沖器接觸到目標航天器時會不可避免地發生回彈現象，因此如何研制出一種可靠性高、緩沖性能好且具有粘附性能的空間緩沖吸附機構已迫在眉睫。同時，傳統的機械設計已經無法滿足日益深入的深空探索需要，而隨著仿生機器人的日漸成熟，將仿生機構應用于太空環境中是未來深空探索的趨勢。

針對仿生緩沖機構，國內外很多學者都開展過相關研究。早在21世紀初期，早稻田大學Hyon等[1]設計了一種仿狗后腿的單腿彈跳機器人“Kenken”，它通過彈簧將機器人跳躍的動能轉變成彈性勢能，從而實現動能的吸收和自身的緩沖；美國俄亥俄州立大學Palmer等[2]設計出一種仿生四腿機器人“Kolt”，其腿部包括大腿、小腿、彈簧和連桿四部分，該機構成功實現了前進時受到較小的沖擊，儲存了部分能量，并且降低了慣性力。到2011年，美國密執安州立大學Zhao等[3]設計出一款仿生彈跳機器人，該機構有三條腿，實現緩沖功能的是一條跳躍腿，另外兩條腿是支撐輔助腿，輔助腿的作用是為了防止機構著陸時發生側翻。國內方面，2013年北京航空航天大學的陳殿生團隊[4]，根據蝗蟲的生理特征和運動特性，研制出一種仿蝗蟲跳躍機構。其腿部由柔性連桿、彈簧、關節和機體組成。該團體對此機構建立了動力學模型，并進行了理論分析[5]，同時利用腿桿抗沖擊法和能量分配法對此機構著陸緩沖時的腿部能量進行分配[6]，最終得到此機構的著陸姿態和腿部能量分配關系的模型[7]。2016年，上海交通大學趙言正團隊[8]研制出一種仿昆蟲六足爬壁機器人，該機器人6條腿徑向對稱，每條腿上有3個電機驅動機器人移動，并配備了吸盤、電磁閥以及真空泵用于機器人的吸附運動。2017年，南京航空航天大學的楊斌[9]設計了一種空間仿壁虎機器人，該機器人利用三維傳感器定量分析仿壁虎機器人的姿態并對其進行姿態調整，在機器人的足墊出黏附基底材料以增加腿部的黏附力，但沒有對機器人的緩沖能力和動力學進行建模分析。

針對空間機器人碰撞方面，清華大學郭聞昊等[10]對空間機器人抓捕目標星的碰撞進行研究，并利用粒子群算法對機器人構型進行了優化；南京航空航天大學岳帥等[11]設計了一種油液-鋁蜂窩緩沖器，以翻倒極限著陸工況為基礎重點研究了多級緩沖器緩沖參數對著陸穩定性能的影響，實現了較好的著陸器緩沖性能；之后，賈山等[12]提出了一種緩沖/行走一體化六足著陸器，重點對其運動學和步態進行了規劃研究，設計出了較好的步態。

對上述文獻分析發現，文獻[1-3]其研究的重點在于機器人的起跳、緩沖能的釋放與回收以及腿部的減震效果，而對機器人的緩沖及吸附過程未涉及過多的研究。而文獻[4-7]重點研究的是機器人或仿生機構的緩沖性能，并沒有實現對目標物表面的黏附功能。文獻[8-9]重點研究的是機器人的吸附狀態，分別使用了吸盤和黏附基地材料增加吸附性能，但對于仿生機構的動力學理論尚未做分析。文獻[10-11]的研究重點在于利用算法和鋁蜂窩材料實現緩沖作用，而對于應用機械腿式結構實現緩沖未做研究。文獻[12]重點研究的是著陸器的運動學和步態分析，而對于著陸器著陸緩沖的關鍵動力學分析未進行介紹與研究。

本文將以蝗蟲的生理結構和運動特征為靈感，設計一種仿蝗蟲腿的空間緩沖吸附機構；并對其進行動力學分析和簡化模型后的碰撞動力學分析；最后結合機構實際緩沖狀態求得其關鍵緩沖參數，從而有效減小機構所受碰撞力且保證其不發生回彈。

1 空間緩沖吸附機構模型的建立

1.1 蝗蟲結構和運動機理

蝗蟲的后腿較為發達，其彈跳運動和著陸緩沖主要依賴于后腿。如圖1所示，蝗蟲的后腿由脛節、關節、伸肌鍵、股節、曲肌腱、伸肌和曲肌共七部分組成。脛節和股節由轉動關節連接，并通過股節肌肉與軀干連接。

圖1 蝗蟲后腿內部生理結構圖Fig.1 Internal physiology of hind legs of locusts

蝗蟲的運動過程包括三個階段，即起跳、騰空和著陸。起跳時，蝗蟲的后腿向地面施壓，腿部肌肉形成彎曲和折疊狀，當蓄力完成后突然釋放肌肉，從而完成跳躍。此過程腿部肌肉包括儲存能量和能量釋放兩個過程，對應的運動為后腿的折疊和伸展兩個運動。后腿折疊時，腿內的曲肌收縮帶動曲肌腱；后腿伸展時，伸肌收縮帶動伸肌鍵。蝗蟲彈跳的能量除了部分存儲在肌肉中外，還有部分存儲在半月結構中，如圖2所示。蝗蟲后腿的脛節和股節通過彈簧狀的半月結構相連，起跳前，蝗蟲的腿部肌肉會帶動半月板；起跳時，半月板瞬間釋放能量促使蝗蟲腿部脛節向后運動，從而完成整個蹬地的動作[13]。

圖2 蝗蟲后腿能量存儲結構示意圖Fig.2 Schematic diagram of energy storage structure of hind legs of grasshoppers

蝗蟲在落地階段，其足部先著地，腿部關節向下緩沖至自身速度降為零。后足的股節和脛節由伸直狀態轉換為褶皺狀態，形成類似彈簧的緩沖效果，從而產生穩定的落地動作。此時，腿部股節的縱向肌肉由自由狀態轉變為拉直狀態，部分動能和勢能轉化為彈性能，存儲在肌肉和半月結構中。在整個跳躍過程中，蝗蟲能有效地進行能量的轉化并保持自身的平衡。

1.2 空間緩沖吸附機構原理圖與樣機設計

根據上文蝗蟲生理結構與功能仿生原理，設計機構腿部為彈性多腿式構型，如圖3所示，其與蝗蟲腿部結構形成仿生映射。其中，關節1和關節2為轉動副，用于機構的緩沖和壓縮；關節間安裝扭簧，用于將機構接觸碰撞時的動能轉化為彈性勢能；關節3為球副，用于適應接觸目標物表面的構型。

圖3 彈性多腿式構型原理Fig.3 Schematic diagram of elastic multi-leg configuration

通過以上構型原理設計的空間緩沖吸附機構的實驗樣機如圖4所示，圖中標有具體零部件。原理樣機腿部呈圓周陣列分布，通過單向軸承驅動關節壓縮，足墊底部黏附有干性粘合劑[14]。

圖4 空間緩沖吸附機構原理樣機Fig.4 Cushion mechanismprincipled sample machine

2 空間緩沖吸附機構受力分析

2.1 空間緩沖吸附機構單腿受力分析

首先建立空間緩沖吸附機構單腿的力學模型。第i條腿的受力分析示意圖如圖5所示。

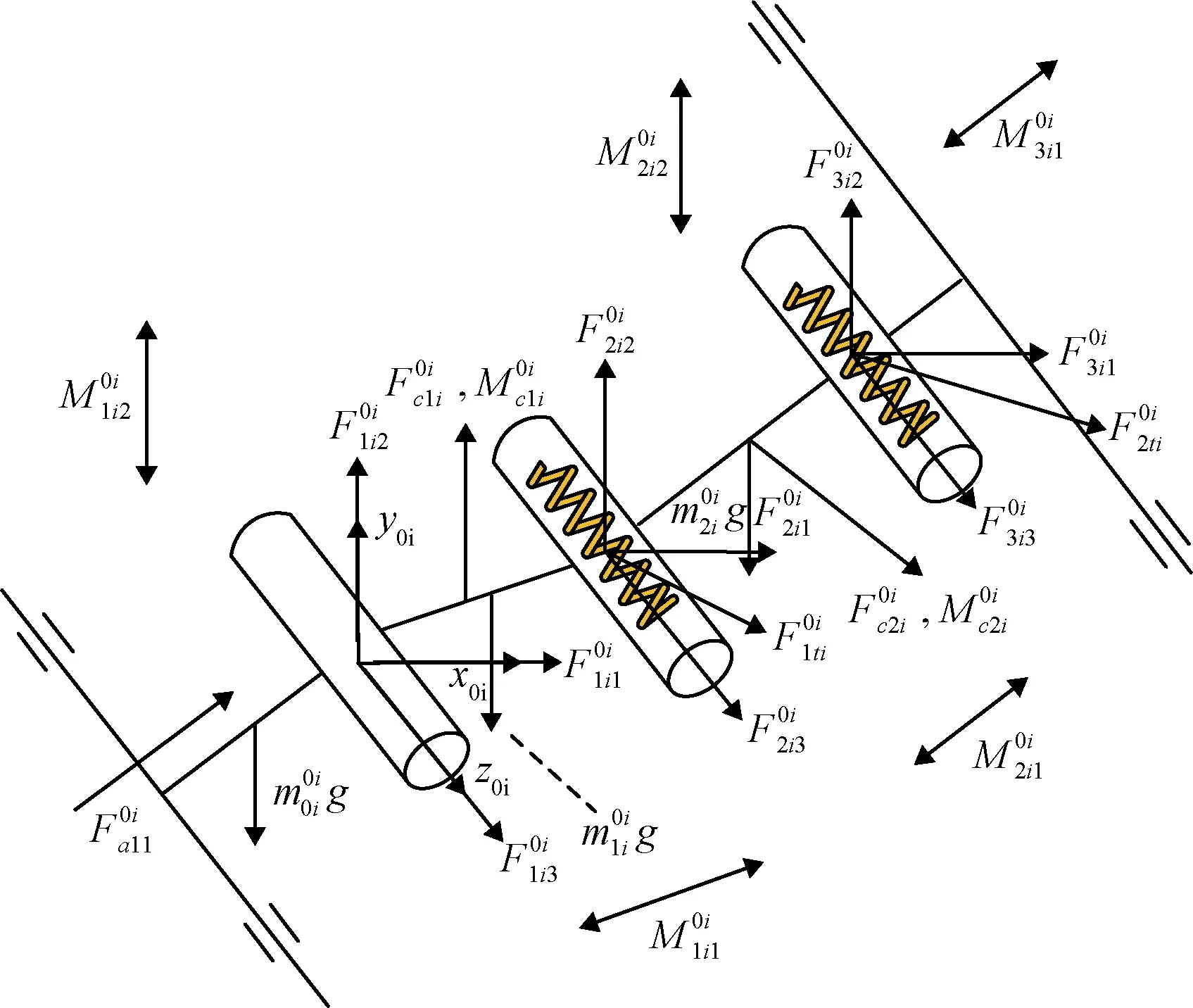
圖5 空間緩沖吸附機構單腿受力分析圖Fig.5 Force analysis diagram of single leg of buffer mechanism

(1)

(2)

將式(2)中脛節和股節的力平衡方程轉化為關于基盤的平衡方程，表達式如下：

(3)

將式(3)分別代入脛節和股節的力矩平衡方程中，得到股節連桿相對于基盤關于y0i的力，這個力是關于空間緩沖吸附機構緩沖距離、緩沖速度和緩沖加速度的函數，表達形式如下:

(4)

2.2 空間緩沖吸附機構整機受力分析

和上文對空間緩沖吸附機構第i條腿的受力分析類似，建立空間緩沖吸附機構整機動力學模型。當機構六腿同時著陸緩沖時，空間緩沖吸附機構整機受力分析圖如圖6所示。

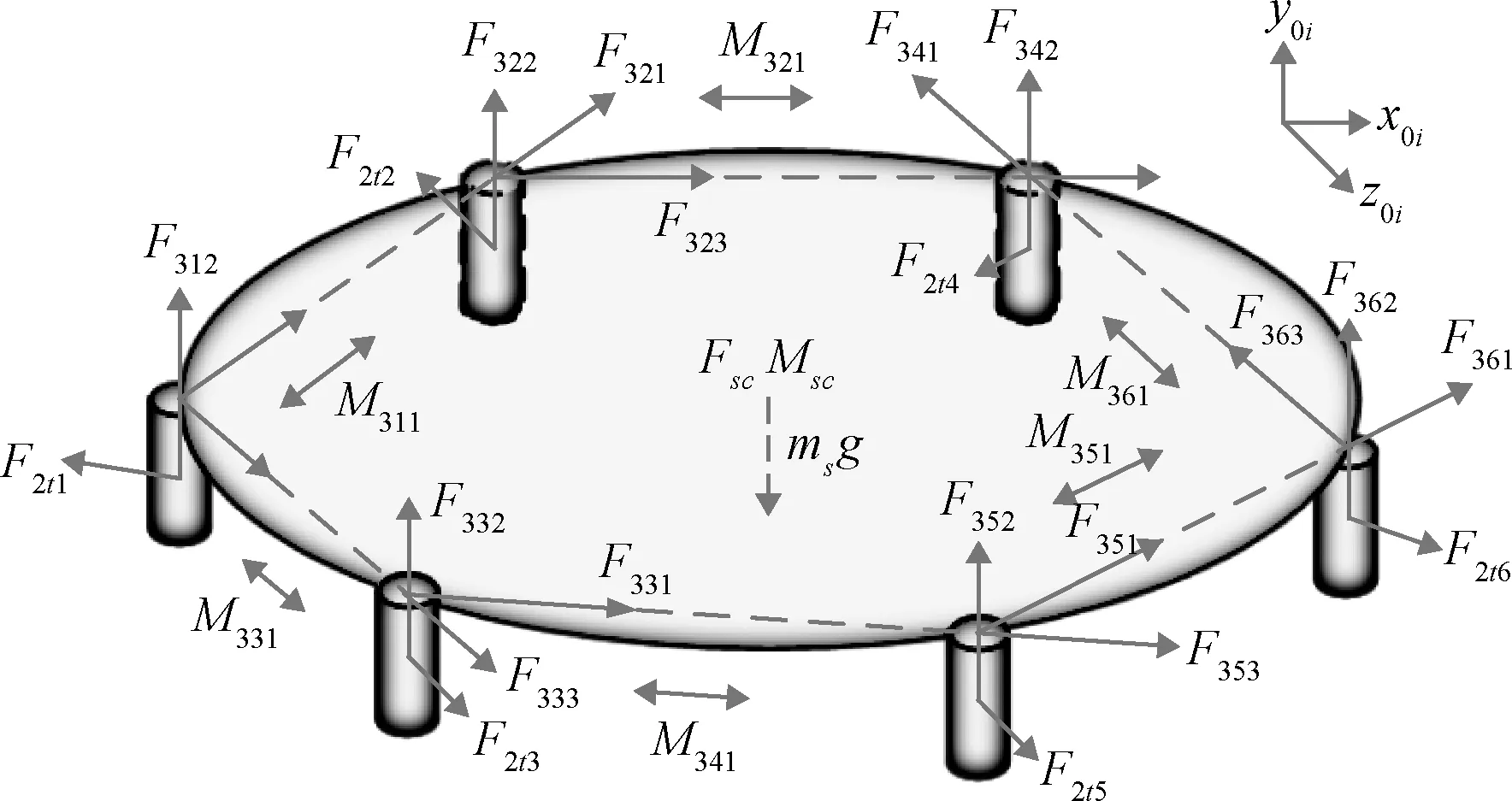
圖6 空間緩沖吸附機構整機受力分析圖Fig.6 Buffer mechanism force analysis diagram

(5)

3 空間緩沖吸附機構碰撞動力學和緩沖參數設計

3.1 空間緩沖吸附機構碰撞動力學建模分析

由于空間緩沖吸附機構的動力學狀態復雜，不宜數學求解，故本文通過建立碰撞動力學模型對機構的運動狀態進行分析。首先需要對機構緩沖碰撞進行如下假設[15]：

1)目標物表面的剛度為無限大；

2)太空微重力環境下重力加速度為0；

3)碰撞接觸力為連續的等效彈簧阻尼力；

4)空間緩沖吸附機構與目標物的碰撞形式為線性質量彈簧阻尼系統；

5)碰撞產生的頻率遠大于空間緩沖吸附機構內部的頻率；

6)目標物的質量遠大于空間緩沖吸附機構的質量；

7)碰撞內所有接觸都為點接觸。

根據以上假設，建立空間緩沖吸附機構碰撞黏附目標物原理圖以及碰撞動力學模型，如圖7所示。

圖7 空間緩沖吸附機構碰撞粘附目標物原理圖Fig.7 Schematic diagram of space adsorption mechanism colliding and adhering target objects

在空間碰撞過程中，系統主要的參數是剛度系數和阻尼系數，剛度系數和阻尼系數對應的計算參數是接觸時間和恢復系數，簡化模型后可以用空間緩沖吸附機構的剛度系數和阻尼系數來代替。其中，接觸時間是指空間緩沖吸附機構和目標物碰撞的時間，恢復系數是指碰撞后空間緩沖吸附機構和目標物的相對速度比上碰撞前空間緩沖吸附機構和目標物的相對速度，恢復系數越小則機構碰撞后反彈越小，為0時表示空間緩沖吸附機構和目標物共同運動。

(6)

式中：kc和cc分別是空間緩沖吸附機構腿部末端足墊碰撞目標物表面的剛度系數和阻尼系數，xt和xf分別表示目標物mt和空間緩沖吸附機構腿部末端足墊mf的位置,mt是空間目標物的等效質量,mf是空間緩沖吸附機構末端足墊的等效質量。根據式(6)，可得圖7中各質量體的動力學方程為：

(7)

假設圖7所示模型不存在阻尼，即恢復系數為0，則空間緩沖吸附機構碰撞的頻率可以表示為:

(8)

式中：ωf,ωc和σ分別表示為:

(9)

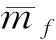
(10)

根據建模假設條件(5)，碰撞產生的頻率遠大于空間緩沖吸附機構內部的頻率，即ωf?ωc；根據建模假設條件(6)，目標物的質量遠大于空間緩沖吸附機構的質量，即mf?ms,ms?mt，因此，可得：

σ≈1

以上分析情況為機構不存在阻尼，而在實際碰撞的情況下，機構必然存在一定的阻尼。本文已假設碰撞產生的頻率遠大于空間緩沖吸附機構內部的頻率，所以在實際情況下，碰撞面接觸產生的頻率會比空間緩沖吸附機構自身產生的振動頻率衰減的更快。所示上式可以用空間緩沖吸附機構的振動頻率來等效替代：

(11)

式中：ωf表示為：

(12)

(13)

圖8 空間緩沖吸附機構碰撞目標物動力學簡化模型圖Fig.8 A simplified kinetic model diagram of a space adsorption mechanism impacting a target

此時，碰撞動力學方程可以表示為:

(14)

式中：y表示為空間緩沖吸附機構彈簧的位移量。

3.2 空間緩沖吸附機構緩沖參數的設計

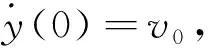
(15)

式(15)表示空間緩沖吸附機構碰撞目標物表面后機構的振動方程。式中:ω表示空間緩沖吸附機構的固有頻率，表示為：

(16)

式中:γ表示碰撞時的阻尼系數，表示為：

(17)

由式(15)，可得空間緩沖吸附機構的碰撞時間為振動頻率周期的一半，表示為：

(18)

由上式可得，阻尼系數的取值范圍為0≤γ≤1。

如果當阻尼系數大于1時，根據公式(18)，則表示空間緩沖吸附機構與目標物平面的碰撞時間為無窮大。根據求得的接觸時間，可以求得空間緩沖吸附機構碰撞時的剛度系數，即等效為求解空間緩沖吸附機構的恢復系數ε，通過式(18)可得：

2.2 測定方法 用卷尺測定樹高、冠幅、干高，用角度尺測量枝條開張角度；處理組和對照組骨干枝上選取飽滿度一致的側芽134個，調查萌發率、抽生新梢類型；處理組和對照組各選取134條中短枝，調查頂花芽數量；全樹采果測定產量。

(19)

式中:阻尼系數取值范圍同樣為0≤γ≤1，當阻尼系數大于1時，此時碰撞恢復系數方程不成立，即恢復系數為0，表示空間緩沖吸附機構和目標物粘合后一起運動。

根據機構的設計要求，本文設計的空間緩沖吸附機構要求機構碰撞目標物后粘附在目標物的表面，即機構不發生反彈或反彈概率極小，所以這里以碰撞恢復系數為0的理論值代入公式進行設計，即阻尼系數大于1的情況。根據原理樣機的實際質量為1.3488 kg，且目標物的質量遠大于空間緩沖吸附機構的質量，設定目標物的質量為10000 kg，碰撞時空間緩沖吸附機構與目標物平面接觸的是機構腿部的足墊，根據假設，其質量又遠小于空間緩沖吸附機構的質量，為0.0192 kg，可求解得：

1.3486 kg

空間緩沖吸附機構的恢復系數方程如式(17)，將質量系數代入式(17)中，等式兩邊平方,可得關系式

(20)

令碰撞恢復系數方程為1.01，得

(21)

此時，取空間緩沖吸附機構扭簧的總剛度系數為0.8 N/mm，得阻尼系數為6.635×10-2N·s/mm。

3.3 仿真校驗

利用ADAMS動力學軟件對上述緩沖參數進行仿真校驗。將機構緩沖參數分別設置為不同的剛度系數和阻尼系數模擬碰撞的過程，空間緩沖吸附機構的接觸速度為0.6 m/s。仿真校驗的參數根據緩沖參數大于1和小于1進行設置，同時根據空間緩沖吸附機構的回彈情況，參數序列1、2、4為緩沖參數大于1的情況，即空間緩沖吸附機構不發生回彈；序列3為緩沖參數小于1的情況，即空間緩沖吸附機構發生回彈。序列1、2、4通過控制系數法進行參數設置，其中序列2是未計算優化前的機構緩沖參數。如圖9所示是空間緩沖吸附機構仿真碰撞前后狀態的示意圖。通過仿真得到如圖10所示的碰撞力結果曲線圖和如表1所示的仿真結果集。

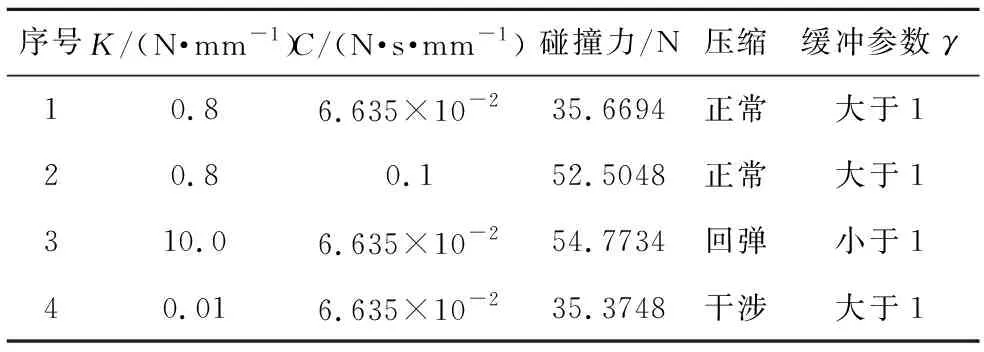
表1 ADAMS仿真結果集Table 1 ADAMS simulation results

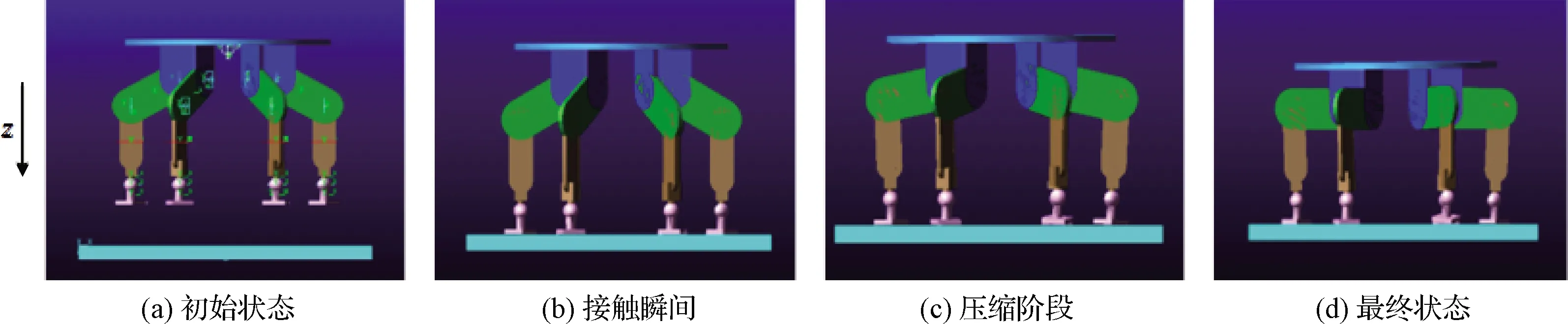
圖9 空間緩沖吸附機構仿真碰撞前后示意圖Fig.9 Buffer mechanism simulation collision diagram

圖10 ADAMS仿真結果曲線圖Fig.10 Diagram of ADAMS simulation results

通過仿真結果可知，在機構不發生回彈的情況下，當空間緩沖吸附機構扭簧的剛度系數一定時，阻尼系數越大，空間緩沖吸附機構所受碰撞力越大，對機構緩沖不利；當阻尼系數一定時，扭簧的剛度系數越小，機構所受碰撞力相差不大，但由于扭簧剛度不夠，此時空間緩沖吸附機構腿部與上端圓形承載臺發生了內部碰撞。當阻尼系數一定時，扭簧的剛度系數越大，機構所受的碰撞力越大，同時空間緩沖吸附機構發生了回彈，導致碰撞時間變長，不符合機構實際的功能需求。

表1中，“正常”是指空間緩沖吸附機構壓縮過程正常，具體是關節正常壓縮、未發生回彈且沒有發生其余碰撞等現象；“回彈”是指空間緩沖吸附機構碰撞后由于緩沖參數設置的原因導致機構發生了回彈，具體是空間緩沖吸附機構碰撞目標物后彈起再落下；“干涉”是指空間緩沖吸附機構壓縮后關節和圓形承載臺發生了內部碰撞，具體是腿部關節碰撞到圓形承載臺的下方。通過仿真校驗分析，驗證了本文緩沖參數設計的合理性和正確性。

4 結 論

1)本文設計了一種新型仿蝗蟲腿的非合作空間緩沖吸附機構，并且提出了空間緩沖吸附機構緩沖碰撞過程的動力學模型。采用連續性碰撞方程進行研究，將空間緩沖吸附機構等效為線性彈簧阻尼結構。再結合實際緩沖碰撞模型參數設計了空間緩沖吸附機構的緩沖參數。

2)仿真結果相較于未計算優化的剛度系數和阻尼系數，機構所受碰撞力已大幅度減小約32%(序列1與2對比)，且未發生回彈和干涉現象。表明該方法的合理性和正確性。本文對于空間緩沖吸附機構一次性著陸緩沖具有一定的理論意義和工程應用價值，適用范圍為可等效為彈簧阻尼結構的腿式緩沖器與結構。