關于冪等差型水仙花數的研究
韋佳玉,楊健,蔣劍軍
(銅陵學院數學與計算機學院,銅陵 244061)
0 引言
水仙花數是一類廣為人知的正整數。最初的水仙花數是指一個3位數,它各位數字的立方和等于該數自身[1]。例如,153就是一個水仙花數,因為153=13+53+33。眾所周知,3位水仙花數有4個:153、370、371和407。
水仙花數是如此的有趣,以致在眾多的科普學者中口口相傳,也成為編程愛好者推崇的經典案例。比如,談祥柏在文獻[2]中對水仙花數、黑洞與振蕩方面的知識做了科普;馬麗燕等在文獻[3]中以水仙花數為例介紹了Python的程序設計方法;史婉玉等則在文獻[4]中介紹了水仙花數在Java程序設計中的應用。有些學者則從水仙花數挖掘編程的內涵[5]或編程課程對學習習慣的培養[6]。水仙花數甚至滲透到了高中信息技術的學習中[7]。
3位水仙花數是程序設計中的優秀案例。不僅如此,它也是理論探索的一個源泉。林宣治[8]將水仙花數推廣到高位的情況。所謂高位水仙花數,是指一個n位正整數,它各位數字的n次方和等于該數自身。衛洪春[9]則設計了基于C語言動態數組的快速求解算法計算出了所有的高位水仙花數。
近期,楊健在文獻[10]中將水仙花數從高位情形推廣到指數位移情形。所謂位移水仙花數,是指一個n位正整數,它能表示為它各位數字的n+d次冪之和,即:
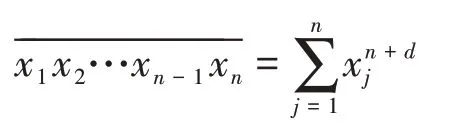
其中d(≥-1)為整數,稱為位移。
本文將經典水仙花數[1]、高位水仙花數[8]及位移水仙花數[10]統稱為齊次水仙花數。
繼3位水仙花數之后,尋找齊次水仙花數成為編程進階的優秀案例,有著獨特的意義。一方面是計算機程序設計教學中典型的程序設計范例,因為尋找水仙花數包含著基礎編程所必需掌握的選擇結構與循環結構;另一方面又是整數理論中一類具有獨特魅力的整數,引出了齊次水仙花數型的不定方程,即形如
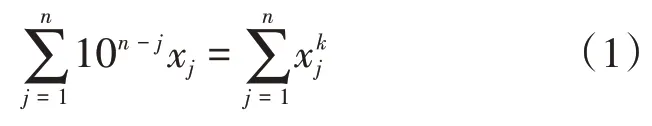
的不定方程,其中xi(i=1,…,n)都是介于0到9的整數,且x1≠0,k為待定次數。文獻[10]提出了關于齊次水仙花數和不定方程(1)的兩個公開問題。
本文將齊次水仙花數的概念做進一步的推廣,提出冪等差型水仙花數。首先給出冪等差型水仙花數的定義,然后討論了冪等差型水仙花數的性質,最后設計了基于Matlab的快速求解算法。
1 冪等差型水仙花數
1.1 定義
設b和d為兩個整數,且b≥0。若一個n位正整數,能表示為它各位數字的如下形式的冪之和:
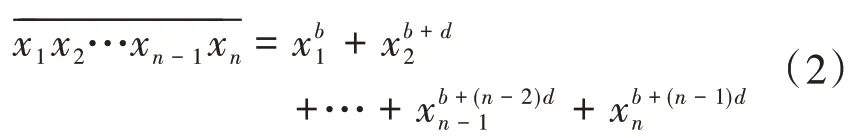
則稱該n位正整數為基數為b公差為d的冪等差型水仙花數。b稱為指數序列的基數;d稱為指數序列的公差。
式(2)中 當d≤0時,令c=-d≥0,a=b+(n-1)d≥0,則(2)式變為:
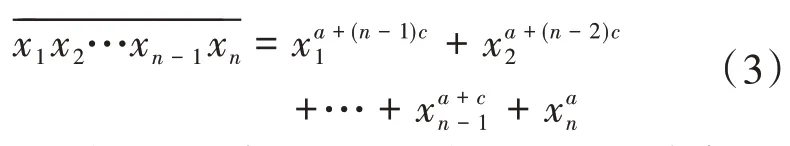
所以,式(2)中當d≥0時稱為冪增型水仙花數,當d≤0式稱為冪減型水仙花數。式(3)正是冪減型水仙花數的直觀形式。
當d=0時的冪等差水仙花數正是齊次水仙花數,所以文獻[10]研究的位移水仙花數是本文的一個特例。
通過計算知,598=51+92+83是基為b=1公差為d=1的冪增數;332=35+34+23是基為b=3公差為d=-1的冪減數;153=13+53+33是b=3的齊次數。
因為位上數字可能有1、0或重復等情形,整數的冪等差表示可能不唯一,比如
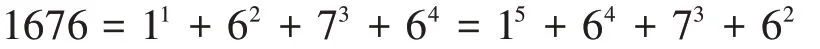
所以1676既是冪增數又是冪減數,原因在于位上數字出現了1和二重數字6。
1.2 性質
因為冪等差水仙花數有兩個參數:數b和d,所以具有比齊次水仙花數更豐富和更復雜從而更難以揭秘的內蘊性質。
性質1有限性條件。設b和d為兩個給定整數且b≥0。則當|d|≤1時,基為b公差為d的冪等差型水仙花數是有限的。
證明設是基數為b公差為d的冪等差數,則式(2)成立。分三種情形證明在題設條件下冪等差數的有限性。
情形1:d=0。已由文獻[10]證明。
情形2:d>0。則式(2)右端可放大為:
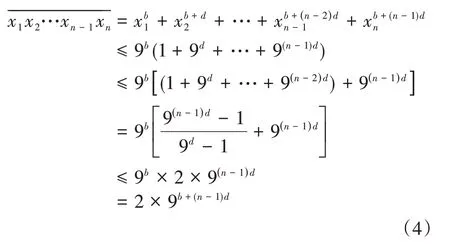
由式(4)進而得:
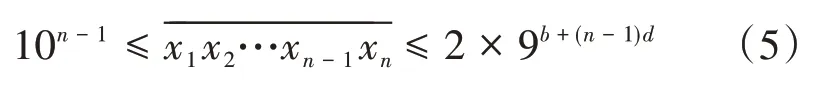
式(5)首尾兩端取以10為底的對數,得:
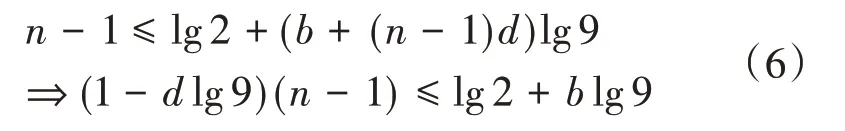
式(6)表明,當d≤1,即d=1時,有:
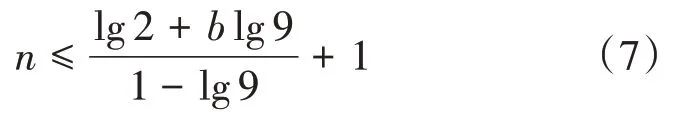
情形3:d<0。則令c=-d≥0,a=b-(n+1)c≥0,由式(2)變為式(3);對式(3)右端進行如式(4)一樣的放大,得到:
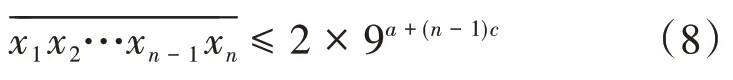
進而得到c=1及與式(7)一致的表達式
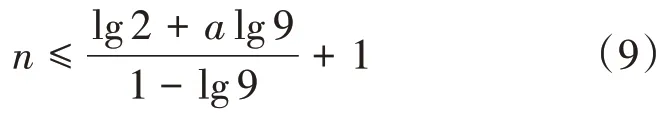
注:性質1表明,對于給定的b(≥1),||d≤1是“基為b公差為d的冪等差水仙花數是有限的”的充分條件。由于式(4)右端放得過大,|d|≤1不可能成為有限性的必要條件。因為公差|d|>1的冪等差數是存在的,比如,463=41+63+35是公差為d=2的冪增數,所以下面兩個問題是自然而然的:
(1)冪等差數的公差d是否隨著位數n的變化而有界?
(2)對于任意給定的兩個整數b(≥1)和d,基為b公差為d的冪等差數是否有限?
性質2n與b和d的關系性質。當||d≤1時,冪等差型水仙花數的位數n與基b和公差d之間滿足如下關系式:

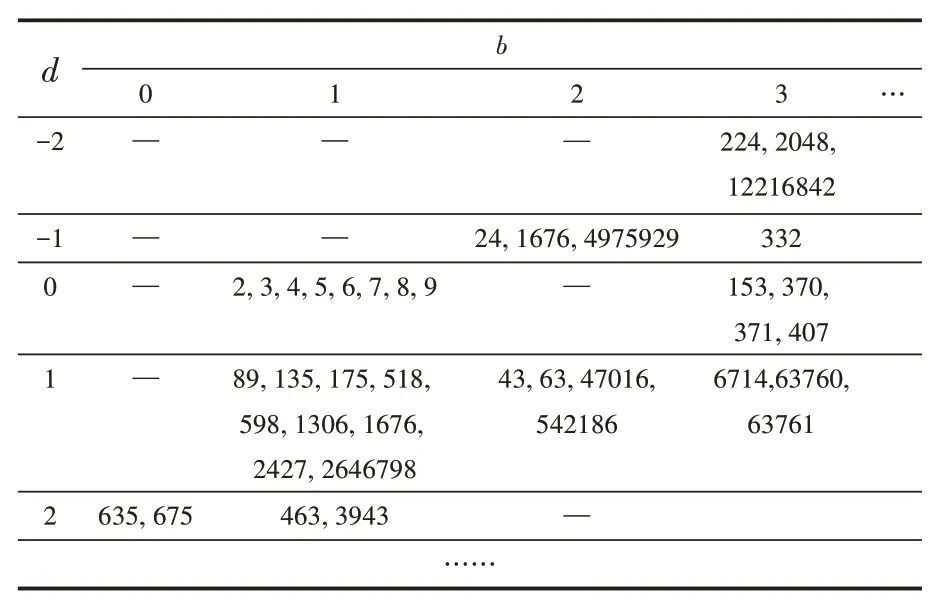
d值0±1關系式n-lg n-1 lg 9 證明(10)式已由文獻[10]給出,(11)式由式(7)給出。 應用性質2的關系式,由Matlab編程計算給定d,b對應的n值的范圍如表1和表2所示: 表1 d=0時n隨b變化的下界和上界 表2 d=±1時n隨b變化的上界 注:應用式(10)和式(11)得到的n的上界和下界,并非n的上確界和下確界。 性質3位異性。假設是 基 數為b公差為d的冪等差型水仙花數,則 (1)位上的數字必有不同于0或1的數字; 證明:反證法先證明(1)。 設n位由0和1構成的正整數是基數為b公差為d的冪等差數,則 又易知,當且僅當n=1,時, 再反證法證明(2)。 設n位正整數是基數為b公差為d的冪等差數。則m是1到9的自然數,由上述1的證明可知,m一定不為1。 于是,有: 又 結合上式,得到: 故 可知當且僅當b=d=1,m=10時,等式成立。與m是2到9的自然數矛盾。故至少有兩個位上的數字不同。 計算冪等差型水仙花數,計算量超大是其典型的特點。文獻[9]設計了高位水仙花數的C語言快速求解算法。本文設計基于Matlab的快速計算泛水仙花數的算法。在設計基于Matlab實現的算法時,須充分考慮Matlab的計算特點。眾所周知,Matlab計算特點是數據以矩陣為單元,循環效率相對較低。所以在設計算法時必須將輸入、輸出和存儲數據都矩陣化,降低對循環的依賴,以提高效率。 算法的核心思想就是基于Matlab以矩陣為計算單元,矩陣化中間計算數據。 (1)將位數為n的所有整數矩陣化,放在變量allnumbers中,即: 在Matlab中這是一個行向量。 所有n位數有k=9*10n-1個。 (2)用Matlab命令套裝num2str、str2num及reshape提取allnumbers中所有n位整數各個位上的數字,構成一個n×k矩陣,放在變量bitsMa?trix中,即: 上述三個語句,第一個語句得到的a是一個字符串行向量,長度為k(n+2)-2;第二個語句是將第一個語句的結果轉置后轉化為整數,所得結果b是一個長度為nk的列向量;第三個語句是將b轉換為n×k矩陣,該矩陣的第j列就是提取出來的第j個n位整數各位上的數字。 (3)將指數序列base+d,…,base+nd轉化為n×k矩陣,放在變量e中,實現語句如下 通過上述語句,即得n×k指數矩陣e。 (4)計算矩陣bitsMatrix的e次冪,并按列求和,結果放在變量esum中,實現語句為: (5)判斷向量allnumbers與esum中對應位置的數是否相等:若相等,是冪等差數;若不等,則不是冪等差水仙花數。 由于9位數以上的數據利用Matlab運算時間過長,我們在這里只計算了9位數以內的冪增型泛水仙花數。 9位數以內的基數為b的冪增型泛水仙花數,且顯然位數為1時只有1是泛水仙花數,故不再計算位數為1的情況。 給定位數n,計算8位數以內的所有冪增型泛水仙花數需要7141.182828秒即約為119分鐘的時間。表3列出了108以內的冪等差水仙花數。 表3 108以內的冪等差數 本文將林宣治、楊健等研究的齊次水仙花數推廣為更一般的冪等差型水仙花數,使得齊次水仙花數成為我們研究范疇的一個特例,并對冪等差型水仙花數的性質進行了研究。 在對冪等差型水仙花數研究的過程中,不禁產生了一些疑惑,其中最大的疑惑就是: 問題1是否存在任意公差的冪等差型水仙花數? 顯然,無論計算機技術發展到什么程度都無法從計算的角度解決上述問題。于是,我們把上述問題等價地轉化為如下數學問題: 問題2下述關于(n;b,d,x1,x2,…,xn)的不定方程 的解是否是有限的?其中0≤xk≤9,k=1,2,…,n,且xn≠0。 期待數學工作者給出問題2的解答。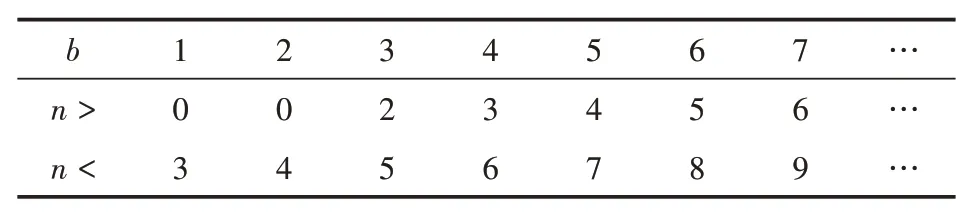

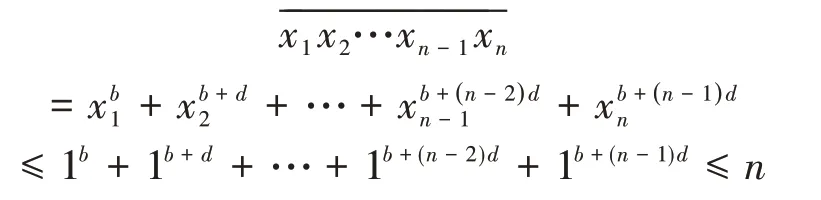
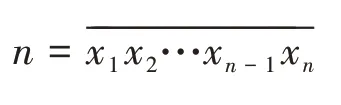
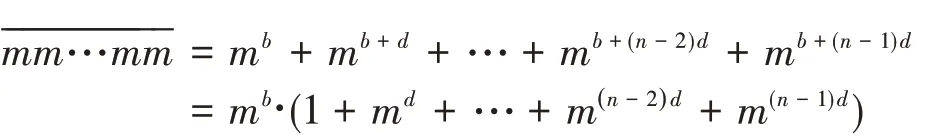
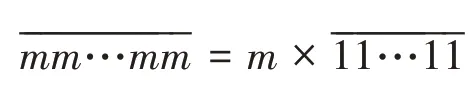
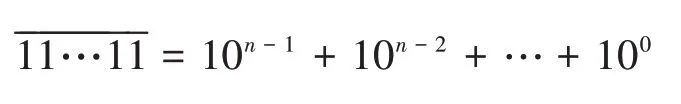
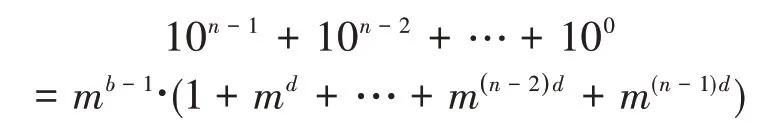
2 冪等差型水仙花數的快速求解算法
2.1 算法描述
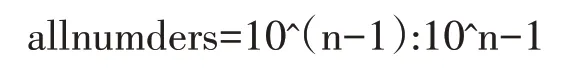


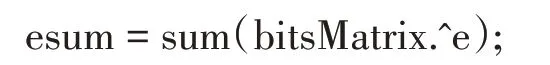
2.2 計算結果
3 結語


