自承式給水鋼管橋鞍式支座的計算方法探討

雷晗 許大鵬

上海市政工程設計研究總院（集團）有限公司 200092

引言

給水鋼管跨越河道、溝渠等障礙物時通常采用自承式鋼管橋結構，其構造簡單，受力明確，能避免水下施工，造價較低且維修方便，因此在我國南方地區得到了廣泛應用。

自承式給水鋼管橋的支座形式有很多，常用的基本形式有滑動式、滾動式和擺動式三類，其中滑動式支座又分為鞍式支座和環式支座兩類。鞍式支座的包角為90°～180°，其結構形式簡單，但與管道之間的摩擦力大，支承部位受力不均勻，一般用于直徑不大于1m的鋼管，鞍式支座的簡圖如圖1所示。環式支座是在支座處的管身四周加剛性支承環，其摩擦力小，支承部位受力較均勻，一般用于直徑不大于2m的鋼管。在這幾種支座形式中，鞍式支座的施工最為方便，因此在自承式給水鋼管橋結構中得到了普遍應用，雖然相關文獻中注明這種支座形式僅適用于直徑不大于1m的鋼管，但在目前已實施的工程案例中，采用鞍式支座的鋼管橋最大管徑已達到DN2200，遠超相關文獻建議值。且在實際工程應用中，根據現有規范理論公式計算得出的管道彎矩相比經驗值往往偏大［1］，從而導致在設計中選用較大的鋼管壁厚而造成工程浪費。

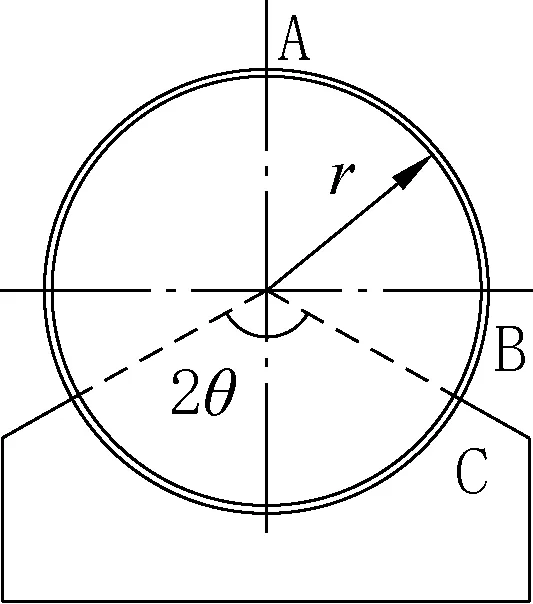
圖1 鞍式支座簡圖Fig.1 Diagram of saddle support

本文對國內外鞍式支座的計算方法進行調研總結，并針對在實際工程應用廣泛的新型支座形式給出理論計算公式，為鋼管橋的結構設計優化提供參考。

1 國內相關研究

《自承式給水鋼管跨越結構設計規程》（CECS214—2006）［2］（以下簡稱《規程》）中對于鞍式支座給出了支承處管壁環向最大彎矩可按下式計算：

式中：κ為鞍式支座處管壁的環向彎矩系數，各極點處的值見表1；R為支承寬度范圍內的豎向反力（N）；r為鋼管內半徑（mm）。

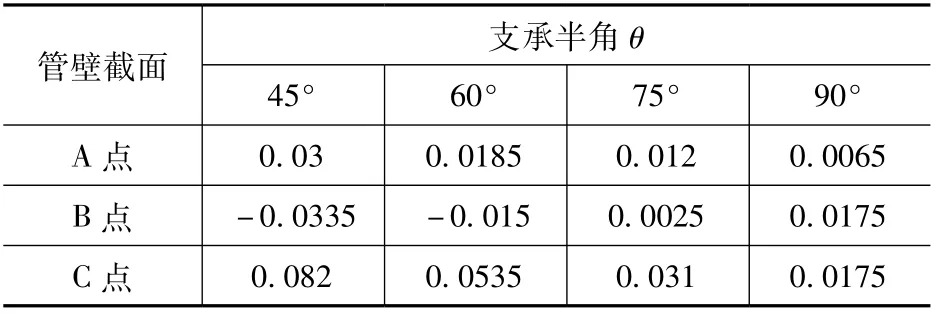
表1 鞍式支座管壁環向彎矩系數κTab.1 Annular bending moment coefficient κ of pipe with saddle support

根據式（1），管壁環向彎矩最不利點為鞍式支座的邊緣處。

該規程6.1.3條文說明中指出，內力計算公式及內力系數表均引自《壓力鋼管》［3］所提供的公式、附圖、附表。

《壓力鋼管》［3］中指出，鞍式支座的優點是簡單，但是其摩擦力較大，鋼管與鞍座不易保證都完全為圓弧緊密貼合，在鞍座邊緣處，鋼管中也產生較大的彎矩，所以不適用于大型管道。該文獻中采用圖表的方式列出了常用鞍式支座管道的彎矩系數曲線。

《倒虹吸管》［4］中提到，地面明管在布置上，多為支墩或非連續支承，淺埋式暗管則為連續管座支承。支墩有鞍座式和滾動式及擺柱式幾種形式，小型鋼管多用鞍座式，包角一般為120°。在管壁與支墩接觸點，焊有加強鋼板，為保證鋼管的軸向伸縮，在加強板與支墩間加有潤滑劑。這種支座當管身產生軸向位移時摩擦力較大，鋼管在支墩處承載能力有限，故只能用于直徑不大于1m的鋼管，支墩間距取5m～8m為宜。該文獻中指出，管底支承反力的分布規律與管道鋪設方式、管道剛度及地基土質有關，對于管底支承反力采用文克勒假定。

2 國外相關研究

日本的地下鋼管實測資料反映［5］：將鋼管鋪設于90°凹圓的土基內，其管底支承反力呈拋物線分布規律。若在硬基上直接鋪管，由于接觸面極窄，管底反力會產生應力集中現象；如果采用包角為90°的混凝土管座，其最大應力將不出現在管頂或管底，而發生在管殼側面，這說明不但基礎形式對管殼應力產生影響，而且基礎剛度也會對管殼應力發生作用。

美國土木工程師學會ASCE《Steel Penstocks》［6］中對鞍式支座進行了如下規定：鞍式支座一般用于管徑和跨度較小（6m～8m）的情況，支承角度一般為120°～180°，角度越小，則管道應力越大，管道的應力分布如圖2所示。規范中給出了管道環向最大彎矩點出現在鞍式支座的邊緣處，其公式為：

圖2 ASCE中鞍式支座的管道應力分布Fig.2 Annular stress of pipe with saddle support in ASCE

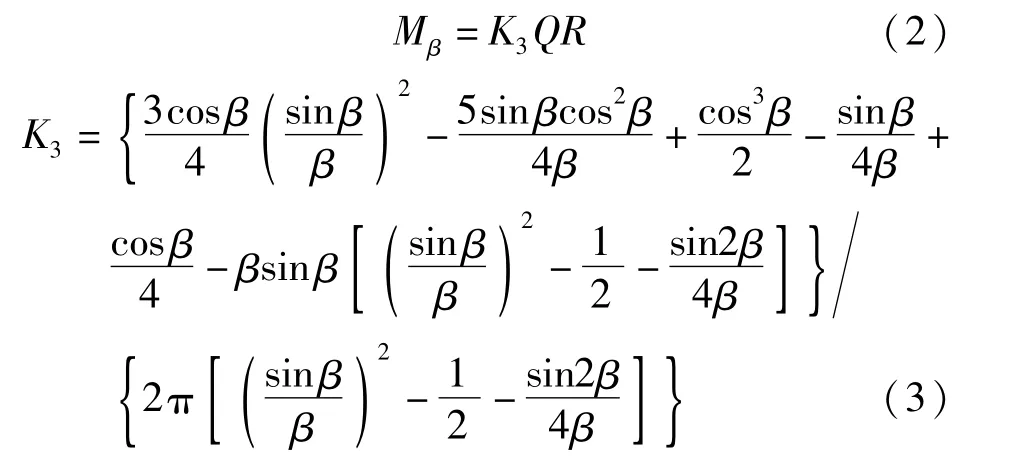
式中：Q為支座處的反力（N）；R為管道半徑（m）；β＝π-θ/2，θ為支承角（°）。

美國水工協會《A guide for design and installation》（AWWA M11）［7］是輸水鋼管設計計算的主要參考依據，該指南中對鞍式支座未給出彎矩的計算公式，但是列出了管道在滿水但無內壓時鞍式支座處的最大應力公式如下：

式中：k為支承角影響因子，k＝0.02-0.00012（β-90°）；β為支承角（°）；P為支座反力（N）；r0為管道半徑（m）；t為管道壁厚（m）。

3 鞍式支座計算方法

3.1 邊界條件推導

根據上述調研，國內對鞍式支座管道環向彎矩的理論計算源自《壓力鋼管》［3］，但該文獻中并未注明相關計算假定及管道環向彎矩系數的理論公式。美國行業規范中給出了環向彎矩最大值的理論計算公式，但也未注明相關計算假定。而美國水工協會指南給出的公式則屬于經驗公式。

通過對比國內外的理論計算公式，可以發現它們之間具有很大的相關性：在支承角范圍內，管道與鞍式支座完全貼合，管道環向彎矩為0。即可由此推斷其邊界條件假定為：在鞍式支座邊緣處，管道與支座耦合，鞍式支座邊緣為管道的固定支座。采用彈性中心法計算，管道環向彎矩系數κ的理論公式如下：

式中：β＝π-θ/2，θ為支承角（°）；α為距A點的角度（°）。

管道環向彎矩系數κ與支承角θ之間的相關曲線如圖3所示，該圖與《壓力鋼管》［3］及ASCE《Steel Penstocks》［6］均能吻合。

圖3 鞍式支座的管道環向彎矩系數Fig.3 Annular bending moment coefficient of pipe with saddle support

要滿足上述假定，管道需焊接固定在鞍式支座處，但焊接固定的支座形式不利于管道的檢修和更換，且會破壞管道外防腐層，因此這與部分實際情況不符。

3.2 新型鞍式支座計算方法

隨著鞍式支座構造形式的發展，華東地區目前已實施的數百座鋼管橋中，其鞍式支座均采用鋼管托或鋼筋混凝土管托，如圖4所示，在管道與支座之間設置不小于10mm的橡膠墊，該橡膠墊一方面保證管道與支座貼合，另一方面也對管道起保護作用，防止管道損傷。

圖4 華東地區鞍式支座構造Fig.4 Structural composition of saddle support in East China

《地下管道計算》［5］中提到，與管頂垂直壓力與管側水平壓力一樣，管底的支承反力及分布規律，對管截面應力及變位（柔性管）都影響較大。目前的管道設計中，對管底支撐反力的處理方法有：試驗分析法、文克勒地基解析法、經驗假定法以及彈性理論分析法等。對于位于土基上的柔性管，支承反力在接觸面上按徑向拋物線式分布，對于位于剛性管座上的柔性管，支承反力在接觸面上按徑向均布，如圖5所示。

圖5 管道支承反力分布（文克勒地基假定）Fig.5 Distribution of pipe reaction force（Winkler foundation assumption）

根據文克勒地基假定，采用這種鞍式支座的管道底部可視為剛性管座，支承反力可按徑向均布計算，在橡膠墊的作用下，也可以進一步地將支承反力平均化。相應地，管道環向彎矩系數的理論計算公式如下：

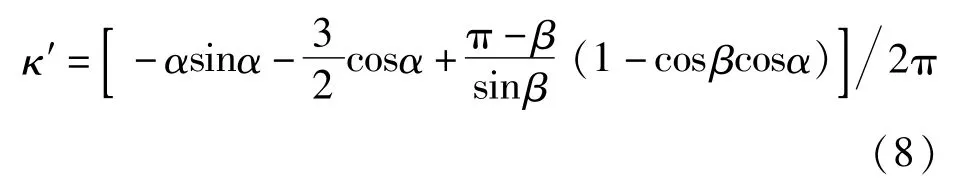
管道環向彎矩系數κ′與支承角θ之間的相關曲線如圖6所示，隨著支承角度的增大，管道環向彎矩系數逐漸變均勻。采用固定支座假定和采用反力徑向均布假定的管道環向彎矩系數最大值對比見表2，在θ＝90°和θ＝150°時兩者的數值基本相近，在θ＝120°和θ＝180°時后者比前者減小較多，尤其對于常用的180°支承角，最大環向彎矩系數減小至約83%，新型支座形式能較大地減小管道內力。

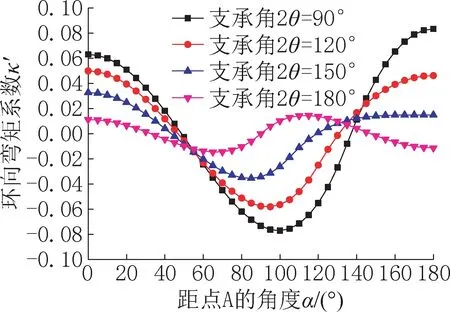
圖6 鞍式支座的管道環向彎矩系數（反力徑向均布）Fig.6 Annular bending moment coefficient of pipe with saddle support（radial uniform counter-force）

表2 鞍式支座管壁環向彎矩系數對比Tab.2 Comparison of annular bending moment coefficient of pipe with saddle support

4 結論

鞍式支座廣泛應用于自承式給水鋼管橋中，通過調研國內外相關研究，并與實際工程案例對比，可得出以下結論：

1.國內外的理論計算公式均假定鞍式支座邊緣為管道的固定支座，在支承角范圍內，管道與鞍式支座完全貼合，管道環向彎矩為0，即管道需焊接固定在鞍式支座處。

2.根據文克勒地基假定，對于底部設置鋼管托或鋼筋混凝土管托的管橋，管道與支座之間設置橡膠墊，管底支承反力在接觸面上可視為按徑向均布。

3.本文中給出了針對新型支座形式的管道環向彎矩系數的理論計算公式，對于常用的180°支承角，管道環向彎矩計算值能顯著減小。