萊比塘銅礦特高品位的識別與處理方法研究
李 健, 任 太 平, 黃 曉 華, 趙 天 雷
(中國水利水電第十工程局有限公司,四川 都江堰 611830)
1 概 述
蒙育瓦萊比塘(Letpadaung)銅礦系特大型露天銅礦,位于緬甸聯邦共和國西北部實皆省(Sagaing)南部,簡稱L礦。L 礦位于兩山包及中間溝谷之下,為隱伏礦床,整體呈一個頂面平整的金元寶型,走向NW,走向長約2 200 m,寬約1 400 m,產狀基本水平。礦體平均厚度約143 m,平均品位為0.37%。L礦Cu邊際品位為0.1%。
目前,該項目已進入生產采剝期,在實際生產過程中,爆區圈定的礦體平均品位對采礦生產和選礦工作起到了重要的指導作用,是控制礦石貧化率和損失率的重要依據。在計算平均品位時,常出現特異的極值品位。這種極值品位若處理不當,常常會影響到爆區平均品位的計算結果,因此,對爆區特高品位處理方法進行研究很有必要。對特高品位的識別與處理方法研究進行了闡述。
2 爆區極值品位的識別與處理
“由于礦石組分的不均勻性和取樣方法、取樣手段及取樣主體的偶然性,在樣品采集過程中偶爾會出現個別樣品的品位值比全部樣品的算術平均值高得多的品位,稱之為特高品位”[1]。但是,忽視這些特高品位的樣品是不恰當的。雖然其在全部樣品值中只占少部分,但它對爆區平均品位值的統計結果影響較大。倘若將特高品位不經處理即直接用于爆區平均品位的計算,尤其在樣品數較少時,將會導致高估金屬量,進而為后續浸出率的計算帶來較大的誤差。因此,有必要對極值品位的樣品處理進行系統的研究。
特高品位的處理方法主要有剔除法和替代法。但為了不損失信息量,不能簡單地使用剔除法將特高品位直接剔除,采用更多的方法是用固定的上限值代替特高品位值。
2.1 目前采用的識別與處理方法
“處理特高品位值常用的方法主要有傳統方法、經典數理統計法、地質統計學法等。傳統方法主要為經驗類比法,其根據礦床類型與礦石品位變化特點,將品位值高于爆區品位算術平均值5~12倍的值定為特高品位,當爆區內品位變化系數大時取上限值;當爆區內品位變化系數小時取下限值。經典數理統計法主要依據樣品均值、3倍標準差、變異系數以及分布密度函數曲線上拐點值識別和處理特高品位值。地質統計學法主要包括估計鄰域法和影響系數法”[2]。
目前萊比塘銅礦項目采用傳統方法確定特高品位下限值,用經驗法取高于整個萊比塘平均品位(0.4%)的10倍(4%)為特高品位的下限值。處理特高品位的方法是用確定的特高品位(4%)下限值代替特高品位。
傳統方法主要是根據人為的經驗識別和處理特高品位,其結果因人而異,這種方法相對簡單,在萊比塘項目的運用也一直被業主所認可。由于有幾條大的構造帶穿過萊比塘礦體,礦體品位受構造和蝕變影響比較明顯,因此,爆區在不同區域品位變化比較明顯。“在低品位爆區運用傳統方法相對比較實用,但是在高品位爆區簡單使用這種方法所取得的計算結果就有待研究”[3]。在萊比塘礦目前開采境界內的L15 m、L30 m臺階北部以及L15 m到L30 m南部已經出現部分爆區硅化特別明顯的情況,其黏土含量很低。銅品位特別高的爆區,如L30-1110爆區,在該爆區采用傳統方法處理特高品位,發現有12個特高品位,用4%代替后得到的平均品位值為1.39%,其計算結果明顯偏低。
2.2 采用影響系數法處理特高品位

最終采用GL代替特高品位值”[4]。
利用影響系數法處理L30-1110爆區數據,將影響系數k設為5%時,得出爆區的平均品位為1.55%,且未發現特高品位。由此可以看出:該爆區整體品位偏高且沒有影響整個爆區平均品位5%以上的單孔品位;如果仍采用傳統特高品位處理方法會造成整個爆區的平均品位值比理論品位值偏低,因此,使用傳統方法處理極值品位不完全適合于所有爆區平均品位值的計算,而影響系數法可以比較科學的處理爆區極值品位,從而得到更接近爆區理論品位值的平均品位值。
影響系數法不適合數據量很多的情況。因為影響系數法需要經過多次掃描才能識別與處理特高品位。根據影響系數法的原理,影響系數法在使用前需要確定影響系數k值,而不同的k值得到的結果亦會不同。為了更加科學的對k值進行選取,需做專門的研究。
2.3 影響系數法k值的選取
對于使用影響系數法進行特高品位的識別和處理,影響系數k值如何選取一直是業內爭論的話題。為了解決k值的選取,本次研究以萊比塘銅礦20個爆區的數據作研究樣本進行研究。基于影響系數法,對不同爆區代入k值進行試算求取爆區平均品位值,其中k值的取值范圍為0.01~0.14,將不同的k值在各個爆區對爆區平均品位的影響繪制成以k值為橫坐標、平均品位為縱坐標的平均品位曲線圖(圖1)。
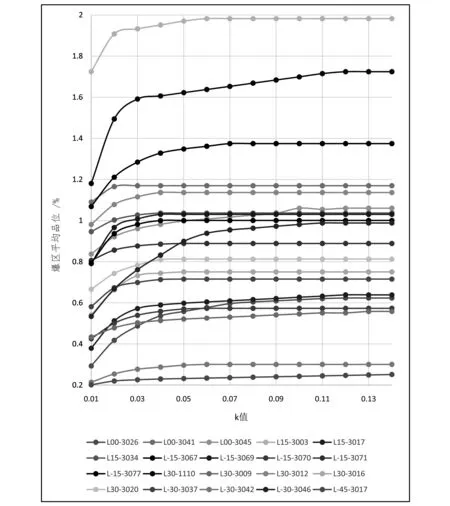
圖1 平均品位曲線圖
對比分析圖1中各個爆區不同k值對爆區平均品位的影響曲線后可以看出:
(1)當0.01≤k<0.06時,絕大部分爆區的品位曲線變化較快,平均品位變化較大。說明k值取在該范圍時,爆區的大部分炮孔品位值被當作了特高品位處理,使爆區平均品位大大降低,這一點明顯不符合特高品位的處理規則。因此,對于爆區特高品位的處理,k值不能小于0.06。
(2)當0.06≤k≤0.1時,大部分爆區品位曲線趨于平緩,平均品位變化不大,僅有少部分爆區品位曲線仍有上升,平均品位有變化。說明k值取在該范圍時,大部分爆區沒有特異值,不需要做特高品位處理,僅有少量爆區存在特異值,需要做特高品位處理。這種情況符合處理特高品位的規則。上述現象在k=0.06時表現的尤為明顯,且礦石品位偏差為2.1%,可以認為k=0.06比較適合萊比塘銅礦的實際情況。
(3)當k>0.1時,僅有極少部分爆區品位曲線有小幅度波動,平均品位基本無變化。說明除極少量爆區的炮孔需要做特高品位處理外,基本爆區不存在有特高品位的炮孔,這顯然不符合實際情況。例如:在L-15-3076爆區中,當k>0.1時,該爆區無特高品位值,故不需要做特高品位處理;當k≤0.1時,該爆區需做特高品位處理。但是,該爆區單孔品位出現的7.13%明顯屬于特高品位值,需要進行處理。因此,當k>0.1時,可能會造成對部分爆區特高品位值的漏處理,從而給平均品位的計算帶來較大誤差。
2.4 3σ準則方法驗證k=0.06的可取性
為了驗證k=0.06的實用性,本次研究通過3σ準則方法加以驗證。“3σ準則方法是一種特高品位處理的方法,它是以爆區平均值加上三倍均方差為特高品位下限值,大于該值的定為特高品位,然后用最大正常值替代特高品位”[5]。通過計算求得的20個爆區平均品位和偏差見表1。
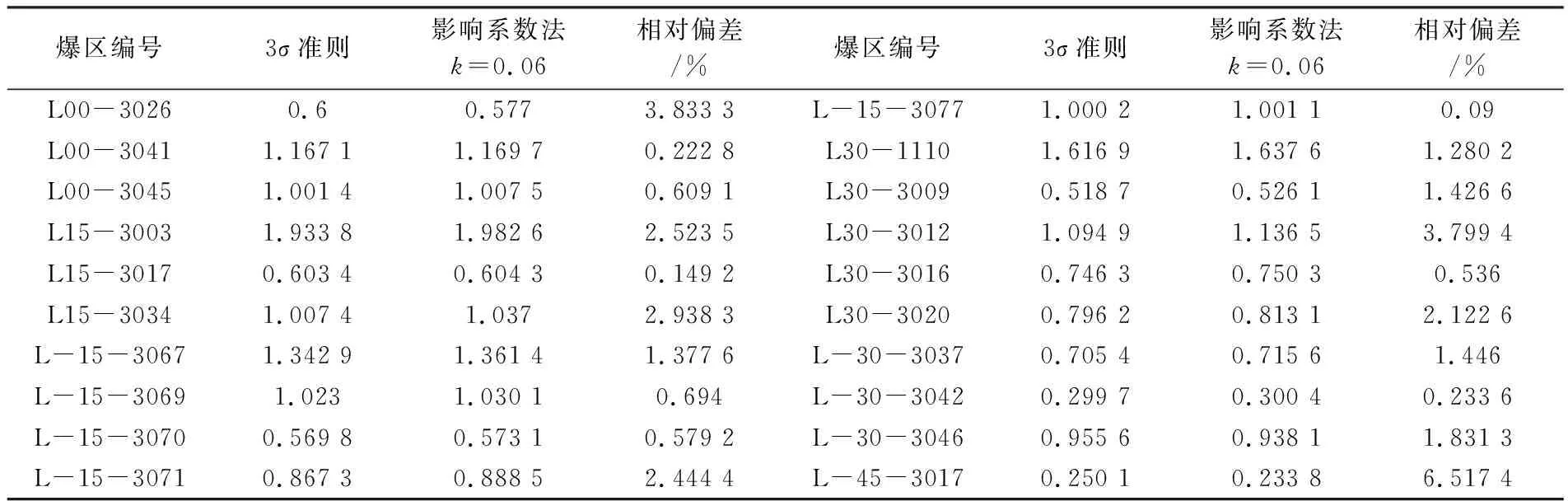
表1 不同方法處理后各爆區平均品位和偏差表
在對比了3σ準則方法處理特高品位和影響系數法處理特高品位后的平均品位,發現在平均品位較高的爆區,兩種方法處理后的平均品位絕對偏差較大:平均品位較低的爆區,兩種方法處理后的平均品位絕對偏差較小。但通過對相對偏差的計算可以看出,兩種方法得到的平均品位值相對偏差不大,基本都控制在5%以內,只有L-45-3017相對偏差為6.52%。通過分析L-45-3017的原始數據得知,該爆區特高品位比普通品位高出約10倍,采用3σ準則和影響系數法的代替值后其有所差別。影響系數法的代替值為0.67,3σ準則的代替值為1.22,二者相差約50%。
將表1中通過兩種不同方法處理特高品位后的平均品位值數據轉化為圖形顯示(圖2)。使用影響系數法,選取k=0.06時,各個爆區進行特高品位處理后的曲線與使用3σ準則方法處理特高品位后的曲線基本吻合,從而驗證了影響系數法在萊比塘銅礦特高品位處理中的可行性與科學性。通過影響系數法處理特高品位后得出的平均品位更接近爆區平均品位真值。故選取k=0.06比較符合萊比塘礦山的實際情況。

圖2 不同方法處理特高品位后的平均品位對比圖
3 結 語
通過研究,得到了以下結論:
(1)在礦體品位受構造和蝕變影響比較明顯的區域,采用傳統方法確定的特高品位值,其計算結果明顯偏低。
(2)當k<0.06時,大部分炮孔的品位將被識別為特高品位并進行處理,從而違背了特高品位的特點,故k值不能小于0.06。當k>0.1時,將會出現爆區特高品位值的漏處理,從而給平均品位的計算帶來較大誤差。當0.06≤k≤0.1時,大部分爆區顯示無特異值,不需要做特高品位處理,僅有少量爆區存在特異值需要做特高品位處理,這一點符合處理特高品位的規則。
(3)通過3σ準則方法加以驗證,影響系數法可以比較科學地處理爆區極值品位,從而得到最接近爆區理論品位值的平均品位值。可以認為:取k值為0.06,比較符合萊比塘礦山目前的情況。

