基于模型預測控制的直升機軌跡跟蹤控制

高莘青，馬 釗，梁穎茜

(航空工業西安飛行自動控制研究所，陜西 西安 710076)

1 引言

實現精準的直升機航跡跟蹤在實際應用中具有重要的意義。然而，直升機氣動特性復雜，各軸(俯仰、滾轉、航向和總距)響應耦合嚴重，操縱較困難[1]。在該背景下，針對軌跡跟蹤問題，近年來提出了眾多的基于非線性理論的控制方法，包括滑模控制[2]，自抗擾控制[3]、反步控制[4]等。大量仿真結果表明上述非線性控制方法能夠保證良好的跟蹤效果。然而，直升機的實際操縱對于系統狀態以及操縱輸入通常具有約束，而非線性控制理論難以同時考慮上述約束，對模型精度要求高，制約了其在工程實施的大規模推廣應用。

模型預測控制(MPC)是工業控制領域應用廣泛的多變量控制算法，并且占據了較大的市場份額[5]。模型預測控制的核心是滾動優化：在每個控制周期內，在已知當前系統狀態以及輸入的前提下，通過預測系統未來的狀態并最小化優化目標，計算系統輸入[5]。利用優化技術計算系統輸入的顯著優勢在于，其能夠融入系統狀態以及輸入的約束，而上述約束在實際應用中通常是需要考慮的關鍵問題。此外，MPC可通過凸優化求解，具有豐富的理論支撐。上述優點保證了MPC在工業界的廣泛應用。

在飛行控制領域，MPC在軌跡跟蹤領域進行了相關研究，可參考相關文獻[6，7]。然而在實施中，需要關注以下關鍵問題。第一，計算代價。理論上，MPC算法可嵌入控制增穩層，也即通過MPC直接計算直升機的周期變距以及總距的控制量。對于工業控制，對象的動態特性比較緩慢，因此MPC的控制周期通常為5s～20s，而 MPC本身的計算代價在實施中并不需要太多關注。然而對于控制增穩回路，控制周期約為10ms，且飛控計算機算力有限，難以實時支撐MPC的在線優化。第二，直升機響應類型限制。理論研究通常忽視了各軸實際的響應類型，影響了MPC的實際可實施性。第三，在實際應用中需要合理地整定MPC參數，保證其對各軸響應類型動態不確定性具有一定的魯棒性。

綜上所述，本文主要工作總結如下。第一，提出了基于分層架構的MPC軌跡控制方法：底層控制增穩回路對直升機的速度以及姿態進行調節，而MPC架設在頂層的制導回路，通過對底層回路的姿態和速度指令進行調度，以期實現直升機軌跡的精確控制。與控制增穩回路相比，制導回路的動態特性更加緩慢，可采用更長的控制周期實施MPC，因此顯著降低計算代價。第二，針對直升機典型的各軸響應類型，設計實用的MPC控制策略，確保各軸操縱符合預期。第三，針對實際對象的非線性特性，用了分段線性的方法，保證滾動優化的全局最優性。第四，針對響應動態的不確定性，采用了基于min-max原則的MPC參數整定法，保證了算法的魯棒性以及在不同飛行條件下的可適用性。

2 直升機模型

本文考慮單旋翼以及帶尾槳的直升機對象。根據歐美坐標系，直升機動力學方程、運動學方程和導航方程為

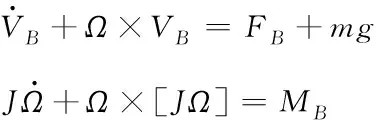
(1)

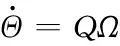
(2)

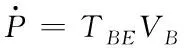
(3)

其中，VB=[VxVyVz]T為機體坐標系下機體線速度，Ω=[pqr]T為機體坐標系下機體角速度，Θ=[θφψ]T為歐拉角向量，P=[xy-h]T為北向、東向坐標和海拔高度，J為直升機的三軸轉動慣量矩陣，Q為歐拉角向量與角速度向量直接的轉換矩陣，TBE為從機體坐標系到地理坐標系的轉換矩陣。FB與MB為機體坐標系下受到的由旋翼以及機體氣動產生的力和力矩

FB=Fmr+Ftr+Ffus

MB=Mmr+Mtr+Mfus

(4)

其中，下標mr、tr、fus分別表示由主旋翼、尾槳和機體產生的力或力矩，詳細的計算方式可參考文獻[8]。直升機主要通過操控主旋翼總距、縱橫向周期變距以及尾槳距，從而改變Fmr、Mmr、Ftr、Mtr，四軸操縱量分別為：縱向周期變距角θ1s，橫向周期變距角θ1c，總槳距角θmr，尾槳槳距角θtr。

3 基于分層結構的MPC軌跡控制策略

3.1 軌跡控制基本架構

對于實際的工程應用，最通用的控制架構是基于時間分離尺度，自底向上依次構建分層次的姿態控制回路、速度控制回路和空間位置控制回路。本文將沿襲上述思路進行軌跡控制回路的搭建。需要注意的是，對于實際直升機控制，需要額外關注直升機的操縱響應類型[9]。由于直升機本身氣動特性特點，飛控系統需要針對不同的飛行狀態設計各軸響應類型。對于軌跡回路的設計，本文主要考慮表1所示的各軸響應類型，說明如下。

表1 直升機各軸操縱響應類型

俯仰通道：帶速度保持的姿態控制響應類型(ACVH)。通過操縱改變機體俯仰角，并通過俯仰角的變化實現機體前向速度的控制。操控回中后，速度保持在當前值上。

滾轉通道：帶姿態保持的姿態控制響應類型(ACAH)。通過操縱控制滾轉角，當操縱結束后，操縱回中，姿態回中。

航向通道：協調轉彎模態(TC)。目標是在機體進行滾轉動作時通過航向軸的控制實現側滑的消除。

總距通道：垂速控制(Rate)。

上述響應類型是直升機在中高速下典型操縱響應類型：縱向操縱直接控制直升機前飛速度，橫向操縱通過改變滾轉控制直升機的偏航角速度，總距操縱直接控制直升機的爬升速度。根據上述的操縱類型，MPC控制架構如圖1所示。MPC架設于頂層的制導回路，通過綜合期望的直升機航跡、位置反饋信息以及對于實際操縱和直升機狀態的約束，實時計算底層回路的前飛速度指令、滾轉角指令以及垂速指令，最終實現直升機軌跡的精確控制。整套控制方案總結如下：通過調整前飛速度指令控制直升機飛行速度，調整滾轉角指令控制直升機的航線方向，調整垂速指令控制直升機飛行高度，而航向通道與滾轉通道進行交聯，在直升機進行滾轉機動時通過調整機頭方向，實現側滑的消除。需要注意的是，盡管直升機的操縱輸入是4自由度，然而對于本文采用的MPC架構，MPC的輸出僅有3自由度，并無航向通道。這是因為內回路航向通道的模態為協調轉彎，其與滾轉回路進行交聯以實現側滑的消除。

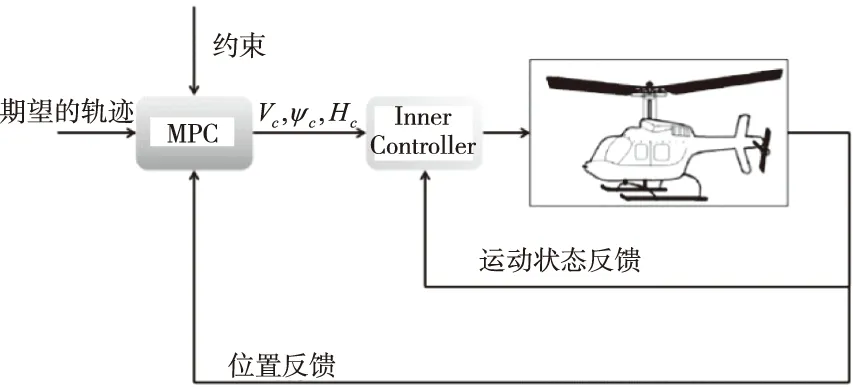
圖1 MPC控制架構

3.2 工程可實施性分析

對于本文采用的控制策略，MPC并未在底層的控制增穩層實施，而是針對各軸實際響應類型，在頂層制導回路架設MPC控制器，通過對內回路指令進行調度，最終實現軌跡的精確控制。盡管MPC作為先進控制算法，理論上可以架設于直升機的控制增穩回路，但是從工程可實施性的角度，本文采取的控制架構具有如下優勢。

第一，有效降低MPC實施的計算成本。直升機內部的控制增穩回路與直升機的穩定性和安全性密切相關，并且由于角速度和加速度響應的快速動態特性，因此需要較短的控制周期。在實際的工程應用中，控制周期在10ms左右。MPC盡管能保證良好的閉環效果，但其核心是優化問題，需要較高的計算代價，而實際飛控計算機算力有限，難以支持MPC的毫秒級的在線實時優化。對于頂層的制導回路而言，其涉及到的響應為速度響應和航向角響應。與角速度和加速度相比，速度響應與航向角響應的動態特性更加緩慢，響應時間通常為秒級。因此，0.1～0.5秒的控制周期通常可以保證制導回路的精準控制。與直接架設在控制增穩回路相比，計算代價至少可以降低90%。

第二，降低了對模型精度的苛刻要求。MPC需要對未來系統的狀態進行預測，因此對模型的精度具有較高要求。直升機動力學具有高度非線性以及強耦合的特點，難以獲取完全精確的模型。在底層通過合理的內回路設計，可以有效地對模型不確定性和耦合進行補償。對于控制增穩回路的設計，PID控制以及模型跟隨控制已經取得了成熟的工程應用[10]。對于本文采用的控制架構，MPC僅需要考慮各軸響應的動態，故建模難度以及模型不確定性將顯著降低。以速度保持和姿態保持為例，內回路通常采用積分器，因此響應模型的增益為1，而響應的動態可基于飛行數據進行估計，因此有效降低了建模過程中的模型不確定性。事實上，閉環響應動態特性的估計是飛行品質評估的核心問題，在工程應用中已有較成熟的解決方案[11]。盡管在不同的飛行狀態下各軸的響應特性具有一定的差異，仍然可以通過整定合理的MPC參數保證閉環控制的穩定性和魯棒性。

4 基于模型預測控制的軌跡跟蹤算法

4.1 MPC優化問題

考慮如下離散形式的系統模型

x(k+1)=Ax(k)+Buu(k)+Bdd(k)+Bww(k)

y(k+1)=Cx(k)+Ddd(k)+Dww(k)

(5)

其中：x(k)為系統狀態向量，y(k)為系統輸出，u(k)為系統輸入，也稱作操作變量，d(k)為干擾變量，其含義為可以測量但是無法直接控制的外擾，MPC通過前饋的機制對其進行補償。w(k)為不可測的高斯噪聲。

在每個控制周期，MPC通過上述系統模型對未來系統狀態進行預測。定義x(k|k-1)為在k-1時刻通過系統模型對k時刻的狀態預測值。在k時刻采集到系統實際狀態，通過如下狀態觀測器對狀態預測值進行修正

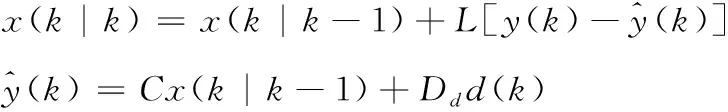
(6)

其中L為誤差反饋矩陣，可采用Kalman濾波理論進行設計。對于預測步長p，系統狀態可根據如下方程預測

X(k)=Γ0x(k|k)+H0u(k-1)+HΔuΔU(k)+HdD(k)

(7)

其中

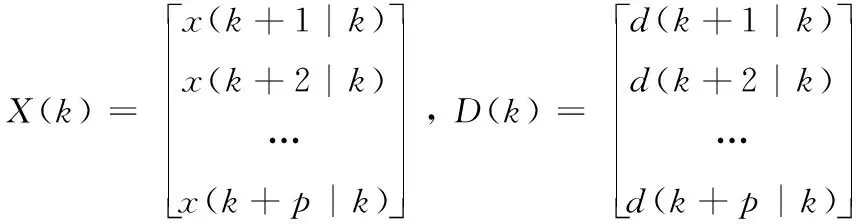
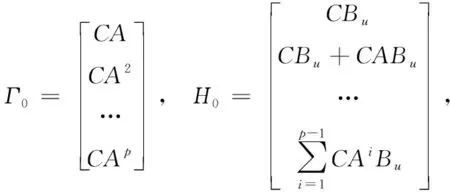
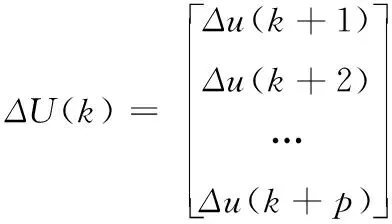
未來時刻系統輸出可根據式(8)進行預測

y(k+i|k)=Cx(k+i|k)+Ddd(k+i|k)

(8)

MPC通過以下帶約束的優化問題計算計算系統輸入[5]

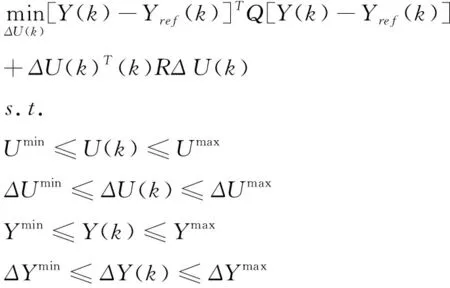
(9)

其中，Y(k)為未來時刻系統輸出預測y(k+i|k)所構成的數據向量，Yref(k)為期望的系統輸出，正定矩陣Q和R為系統誤差加權矩陣。優化目標為最小化跟蹤誤差，并同時保證系統輸入的變化率盡可能平緩。此外，MPC優化考慮了系統輸入和輸出幅值以及變化率幅值的關鍵實際約束。

對于線性系統，MPC問題為凸優化問題，故ΔU(k)對于問題(9)而言是全局最優解。從長期的視角而言，如果模型是完全準確的，且全系統沒有不可測干擾，則ΔU(k)可以保證是系統的最優輸入。然而，由于模型的不確定性或者未知外擾的存在，則系統的預測和真實值存在差異。以長遠的視角，ΔU(k)不能保證長時最優性。故在每一個控制周期內，MPC只實施ΔU(k)頭m個分量，在第m個控制周期之后，通過滾動優化的方式，通過優化問題(9)重新計算系統輸入ΔU(k)并實施前m個分量。通過式(6)狀態觀測器對系統誤差的補償以及滾動優化的形式，保證了MPC的可實施性。

4.2 分段線性MPC

針對第3.1節所述的直升機各軸響應類型，俯仰通道的響應為

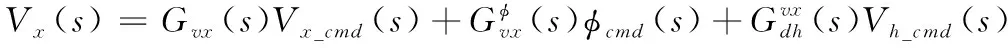
(10)

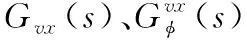
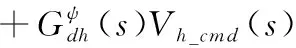
(11)

垂直通道的響應為

+Gh(s)Vh_cmd(s)

(12)

對于MPC的實施，需要對上述傳遞函數進行離散化。對于直升機軌跡跟蹤控制，以地面坐標系為參考。需要注意的是，因為直升機水平面(XY軸)的響應的參考系為機體系，故需要進行坐標轉換:

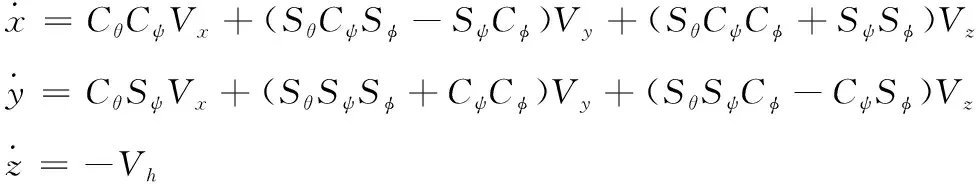
(13)

其中Cθ、Sθ分別表示sinθ和cosθ，[VxVyVz]T和Vh分別為體軸速度和直升機垂直爬升率。

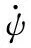
基于上述的MPC控制變量分配，對(13)進行線性化。對于直升機的機動，機體滾轉角和俯仰角在幅值上具有限制，故在線性化的過程中認定SθSφ≈0。線性化的結果為

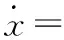
-SCVy-(SCC+SS)Vz

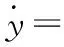
+(SSC-CS)Vz

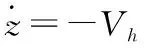
(14)

其中，上標“^”表示在當前控制周期內運動狀態參數的測量值。

5 魯棒MPC的設計

5.1 響應模型形式

基于實際直升機各軸內回路的實際特性，本文采用如下形式的響應模型

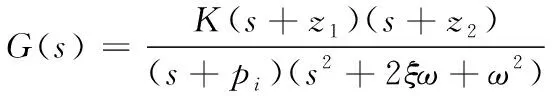
(15)

需要注意到，如果內回路的設計采用了積分器，可先驗獲取模型的穩態增益。在式(10)～(11)中的各軸響應模型中，對角元素的穩態增益為1，故模型參數應滿足如下約束

Kz1z2=piω2

(16)

對于非對角元素可視為其它軸的操縱輸入對本軸響應的干擾，而內回路的積分器可完全消除常值外部干擾，從而模型參數應滿足約束

z1z2=0

(17)

5.2 MPC參數的魯棒設計

內回路的三軸響應模型可利用飛行數據進行辨識，模型獲取的難度相較直升機動力學模型顯著降低。盡管如此，在實際的工程應用中模型仍然存在一定的不確定度。模型不確定性主要來源于兩個方面：

1) 辨識誤差。在進行飛行試驗的過程中，由于測量噪聲或者外擾的存在，導致所辨識的模型存在一定的誤差。

2) 不同飛行條件下響應動態特性的差異，尤其是空速大小的影響較顯著。

對于MPC參數的設計，需要考慮實際的模型不確定性。針對式(15)中的參數形式，本文考慮如下具有參數不確定性的模型：

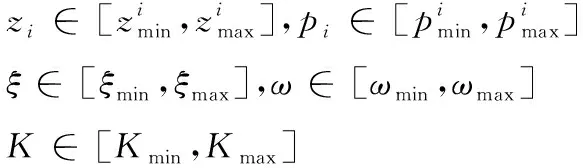
(18)

需要注意，如果內回路采用了積分器，盡管模型具有兩個零點，但是其不確定性僅僅只有1個自由度，因為零點必須滿足約束(16)或者(17)。

影響MPC性能的關鍵參數總結如下：預測步長p、控制步長m、模型輸入輸出權重矩陣Q和R。上述參數通過如下基于min-max準則的優化問題進行優化[12]

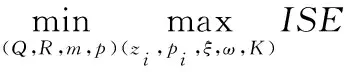
(19)

上述優化問題是雙層優化問題。內層優化變量是響應模型的參數，其目標是對于給定的MPC參數，搜索最壞的控制效果；外層優化變量是MPC參數，其目標是確定最優參數，以保證對于所有可能的響應模型，使得MPC在最壞情況下的控制誤差是最小的，也即最小化最壞情況下的控制誤差。

6 仿真驗證

本節通過數值仿真對提出方法的有效性進行驗證。期望的直升機跟蹤軌跡采用螺旋上升曲線

xref(t)=350sin(2πt/250)+150

yref(t)=350cos(2πt/250)

zref(t)=0.5t

(20)

基于直升機內回路的設計，三軸的指令與響應直接的動態關系見表2。直升機的初始位置坐標為(0，0，0)，偏航角為0rad。基于對各軸內回路動態特性分析，MPC的控制周期設為0.25s。

表2 直升機3軸指令模型

其中，G11(s)～G33(s)傳遞函數為

根據實際直升機的操縱需求，各軸指令應滿足如下約束

-3m/s≤Vx_cmd≤15m/s

|ΔVx_cmd|≤0.6m/s

-1.5m/s≤Vh_cmd≤3m/s

|ΔVh_cmd|≤0.5m/s

(21)

其中，Δ表示變量在相鄰控制周期內的變化量。在確定上述操縱變量的約束后，通過離線優化，預測步長p設置為15，控制步長m設置為1，輸入輸出權重矩陣Q和R分別為diag[1，1，1]和diag[0.115，0.115]，其中符號diag表示對角矩陣。

盡管MPC的控制周期為0.25秒，遠遠高于控制增穩回路的控制周期(10ms)，但是其仍然能夠保證精準的航跡跟蹤效果。MPC操縱變量的求解本質上為凸優化問題，基于已有的快速凸優化技術，在0.25秒內足夠控制步長的求解。

圖2～4展示了3軸的航跡跟蹤結果。由于直升機縱橫的耦合作用，水平面的跟蹤效果與高度軸相比稍差，然而仍然在合理的水平：跟蹤誤差在50秒左右快速收斂到合理的水平，在100秒之后誤差收斂至1.5米以內。

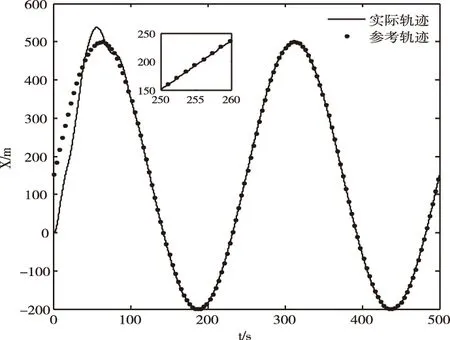
圖2 X軸軌跡跟蹤結果

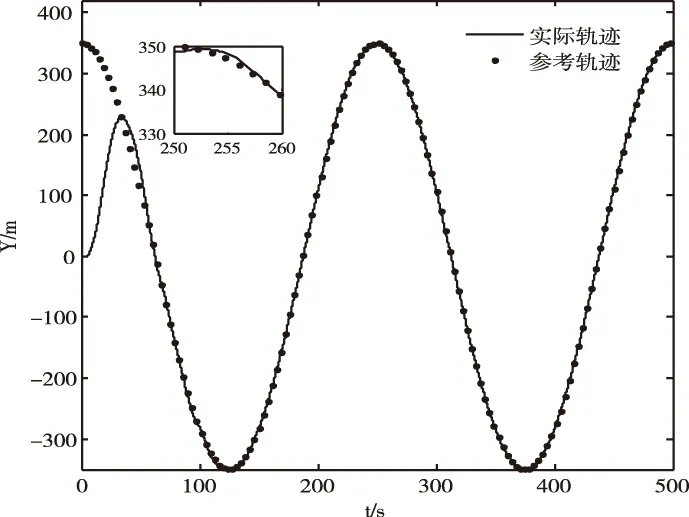
圖3 Y軸軌跡跟蹤結果

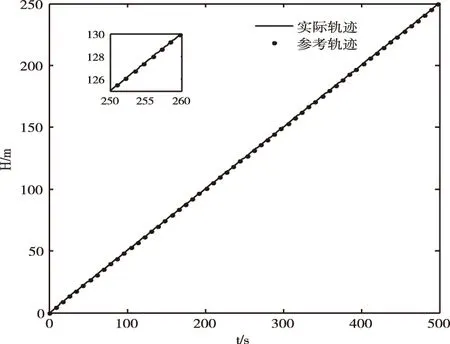
圖4 高度軸軌跡跟蹤結果

圖5展示了3維平面的軌跡跟蹤控制結果：直升機的實際軌跡能夠快速跟蹤參考軌跡，而跟蹤誤差也能快速收斂。上述結果驗證了基于MPC的軌跡控制方法的合理性。

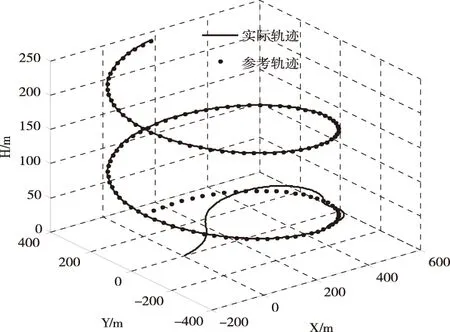
圖5 3維度軌跡跟蹤結果

7 結論

本文提出了基于MPC的直升機軌跡跟蹤控制方法。在工程應用中，直升機具有特定的各軸響應類型。針對實際響應類型的約束，本文提出了基于制導層指令調度的MPC控制架構。一方面，該架構保證了針對不同響應類型的可擴展性，另一方面也能夠確保MPC以更合理的控制周期進行解算，顯著降低了計算成本，保證了工程可實施性。基于分段線性MPC的控制策略擴展了方法對實際非線性過程的適用性。針對實際工程應用中的模型不確定性，采用了依據min-max準則的MPC設計方法，提高了方法的魯棒性。仿真案例驗證對方法的有效性與合理性進行了驗證，結果表明方法控制精度和計算代價合理，具有工程推廣前景。