基于毗域動力學的機身蒙皮疲勞裂紋仿真

王杰鋮，常錦才，祝青鈺

(1. 華北理工大學理學院，河北 唐山 063210；2. 中國航空綜合技術研究所，北京 100028)

1 引言

多部位損傷(MSD，Multiple Site Damage)問題[1]的提出起源于Aloha事故，多裂紋的連通造成了蒙皮結構的破壞。此后，人們發現該問題普遍存在于飛機、火車[2]、橋梁[3]等工程結構中。疲勞裂紋的存在削弱了結構損傷容限特性[4]，嚴重影響了其使用壽命。因此，需要精確的結構健康檢測技術來對結構演變趨勢進行預測分析，以保證結構在設計壽命內的安全性和可靠性，并節約成本。目前，結構損傷模型問題使用最為廣泛的方法是有限元方法(FEM， Finite Element Method)。隋立軍等[5]通過試驗對機身蒙皮試件進行了有限元分析，結果表明了多裂紋的共同作用造成了裂紋擴展速率的增加。學者們在常規有限元方法的基礎上提出了它的改進算法擴展有限元法(XFEM， Extended Finite Element Method)，解決了二次網格劃分問題，節約了計算時間。謝俊杰等[6]利用擴展有限元對滾動軸承內部裂紋擴展問題進行了模擬仿真，計算出裂紋擴展釋放的能量；王綜軼等[7]將擴展有限元法應用于交通信號支撐結構的疲勞壽命預測。這些表征裂紋演變的方法基于物體是連續體這一基本假設，仿真過程對網格具有較強的依賴性。

為實現多部位損傷的機身蒙皮結構裂紋演化仿真，采用毗域動力學方法(PD，Peridynamics)建立疲勞裂紋演化運動方程。該方法摒棄了物體的連續性假設，以離散晶格間的相互作用力形式對宏觀不連續現象進行了重新定義，物體在形變過程中僅需滿足柯西四個基本假設中的能量守恒律，以積分方程的形式來描述選定區域內材料的斷裂情況，避免了導數在不連續處不存在的奇異性。

2 疲勞裂紋仿真原理

毗域動力學最早由Silling提出并得到推廣[8，9]，而后引發了國內學者[10-12]的關注。該方法適用于處理復雜物理模型的建立問題。本質上是對連續性的一種非局部新定義，從微觀角度以積分形式表征宏觀連續現象，避免了在裂紋處求導的困難。

2.1 模型建立

局部思想的裂紋運動方程以Hamilton算子來表征：

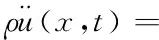
上式的求解需要對應力張量求偏導，在面對復雜物理模型時，方程難以求解。在處理此問題時，以粒子間的相互作用力為出發點，從微觀角度對裂紋進行了重新定義，認為結構上任一點x與該點所視范圍δ內的所有物質點均存在相互作用力，這些完整的力鍵構成了宏觀意義H上的連續，如圖1所示。

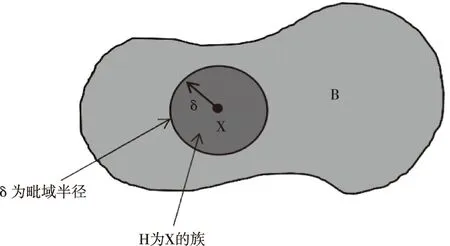
圖1 物質點間的非局部作用

通過對物質點做效果疊加，將裂紋處梯度方程轉換成如下積分運動方程

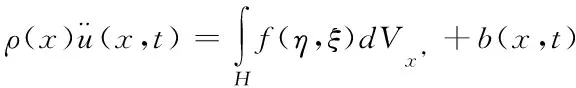
(1)

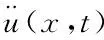
對于彈性材料，點對相互作用f可以由點對間的彈性勢能推出

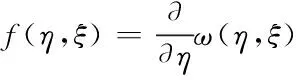
(2)

若材料的拉伸與點對間的彈性勢能呈線性變化趨勢，則

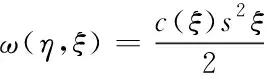
(3)

式中，c(ξ)為微模量函數，表示的是材料點對間鍵的彈性剛度，s是鍵的伸長量

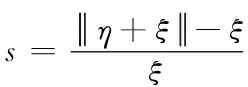
(4)

通過對式(4)積分可以得到毗域范圍內點對的材料斷裂能W

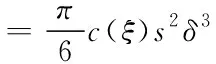
(5)

假設微模量函數c(ξ)=c0是常數，由式(5)與載荷所做的功聯立可得

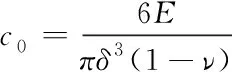
(6)

式中E是材料的楊氏模量，ν是泊松比。

毗域動力學理論中引入了損傷的概念，用于判斷點對間的相互作用效果，當超過了鍵的臨界伸長量s0，則點對間不再存在相互作用，即產生裂紋。對于二維案例，有

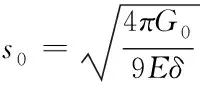
(7)

將式(3)和式(4)帶入式(2)，并聯立式(7)可得點對相互作用力f

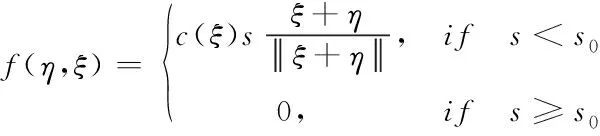
(8)

2.2 模型離散化

根據PD理論將機身蒙皮結構離散成晶格的思想，式(1)可轉換成求解有限和的形式

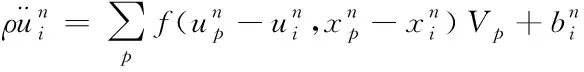
(9)

式中n為時間步長，Vp為節點p處的體積，下表為節點號。

對于線性化模型，有

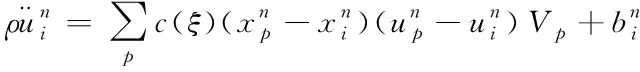
(10)

左邊的加速度場表示為

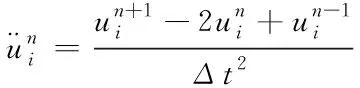
(11)

在式(10)中，為保證方程求解的穩定性，令

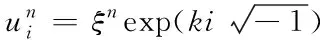
(12)

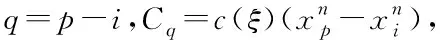
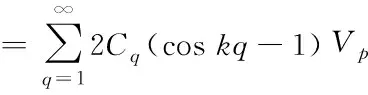
(13)

定義

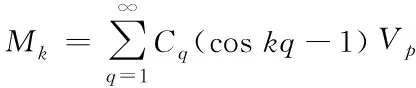
(14)

用式(14)代入(13)求解ξ可得

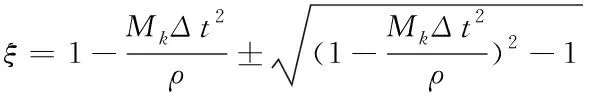
(15)

由于|ξ|≤1，有

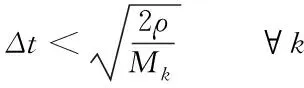
(16)

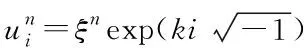
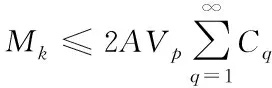
(17)

因此

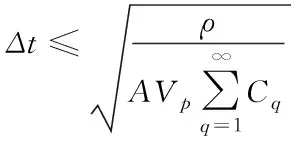
(18)

更加普遍的形式為

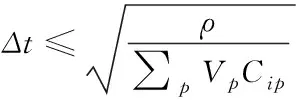
(19)

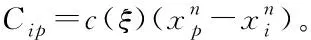
3 仿真實驗

3.1 基于毗域動力學的裂紋演化模擬

以二維含孔機身蒙皮結構為研究對象，假定蒙皮結構是均勻，各向同性的彈脆性材料，蒙皮結構其楊氏模量為192GPa，泊松比為0.3，密度為8000kg/m3，尺寸為長50mm，寬50mm，孔直徑10mm，毗域半徑為δ=3.015Δx，晶格常數Δx為0.5mm，臨界伸長量s0為0.02，節點體積為ΔV=1.25×10-10m3，時間步長Δt=1.0s，時間步數為1000。通過毗域動力學方法模擬裂紋演化結果如圖2所示。

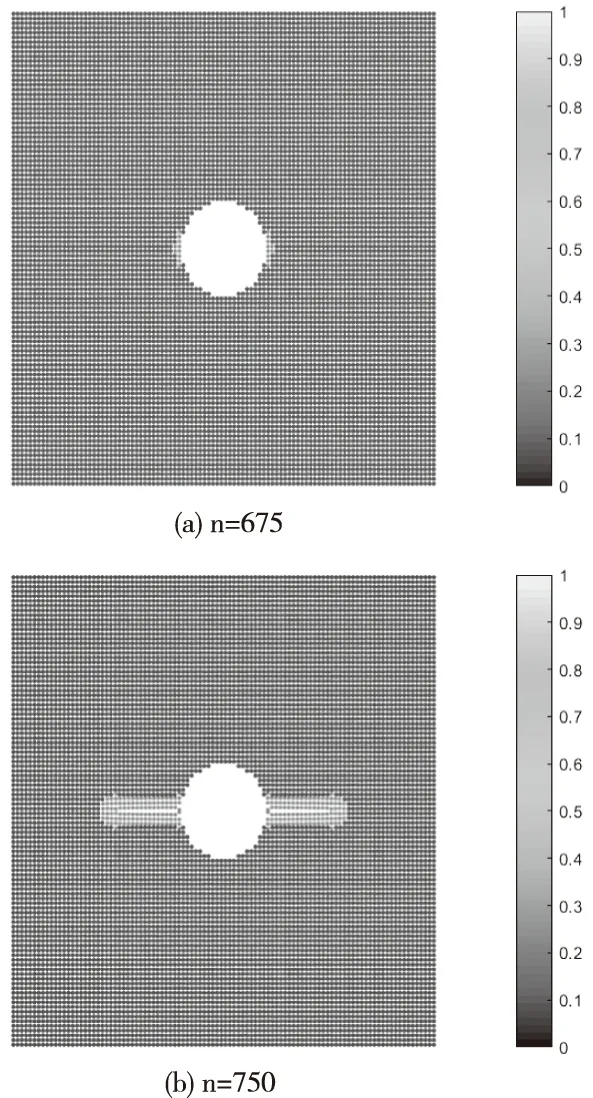
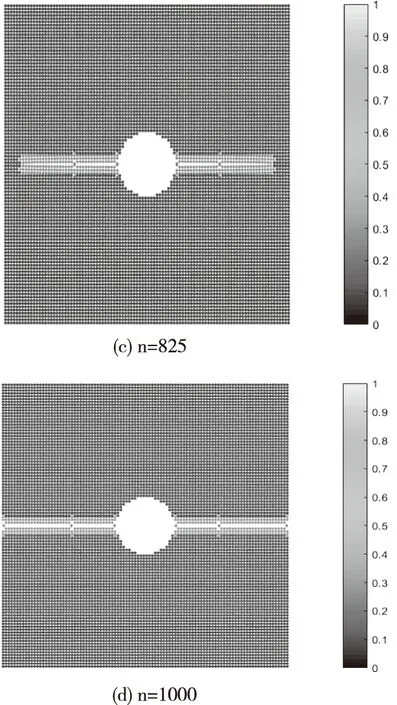
圖2 基于PD的單孔裂紋模擬

如圖2所示，分別對單孔邊裂紋擴展的四個時間步長進行了可視化模擬，在時間步長為675時，孔邊裂紋開始產生，隨著步長的增加，裂紋開始擴展，直至時間步長為1000時，整個機身蒙皮結構破裂。

現行的損傷容限技術考慮的僅是單一裂紋情況，沒有考慮多裂紋的存在，多裂紋連續擴展會產生干涉效應，導致裂紋擴展速率加快、臨界裂紋尺寸減少等現象。因此，多裂紋對工程結構造成的危害遠大于單一裂紋，多裂紋結構剩余壽命預測方法的研究迫在眉睫。針對該問題，采用PD方法對雙孔孔邊裂紋的演化過程進行模擬，結果如圖3所示。

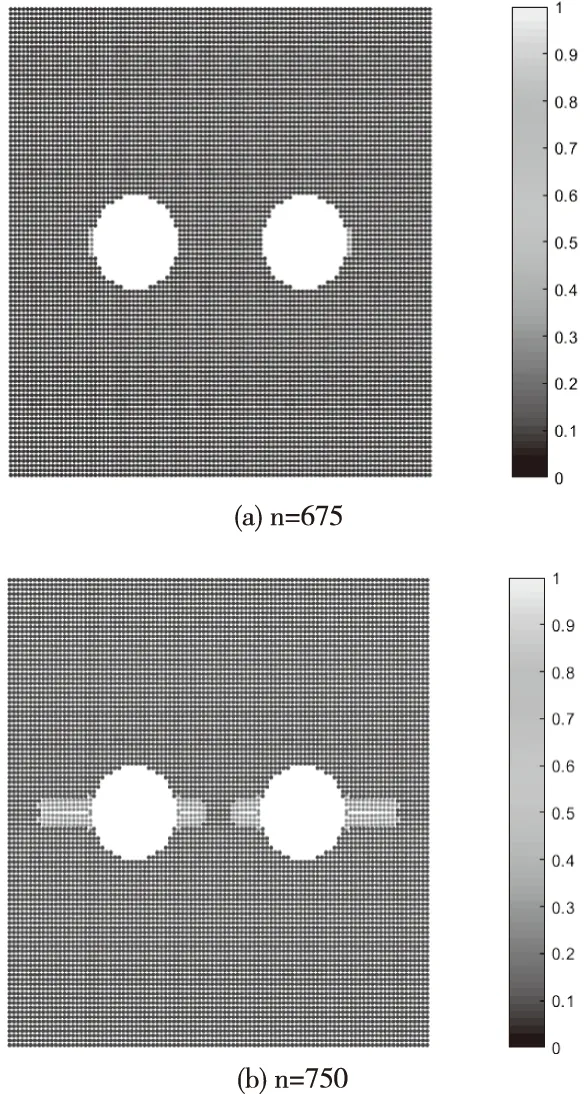
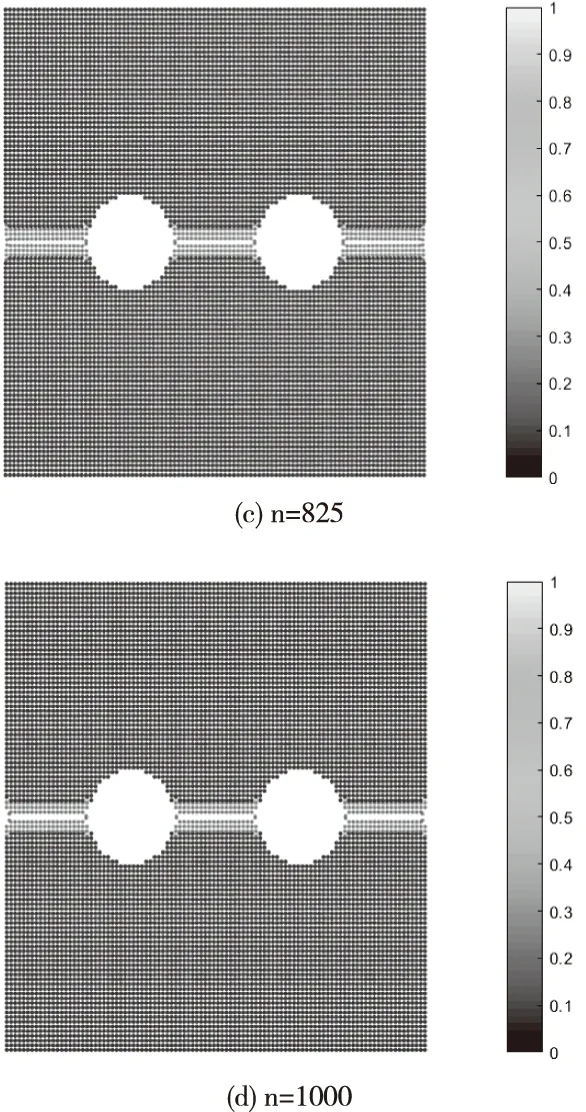
圖3 基于PD的雙孔裂紋模擬

通過圖3雙孔孔邊裂紋演化的模擬可知，在時間步長為675時，雙孔孔邊外側裂紋開始萌生，在時間步長為750時，雙孔內側裂紋擴展長度小于外側，在時間步長為825時，雙孔之間的裂紋已經聯通，整個結構就已基本破裂。驗證了在多裂紋存在的情況下，由于干涉效應的存在，導致了裂紋擴展速率的加快，加速了機身蒙皮結構的破裂。

上述仿真基于理想狀態下進行，離散化的每個粒子在受外力情況下具有相同的初速度，產生了對稱的疲勞裂紋。在通過MTS Landmark電液伺服疲勞試驗機系統對多種金屬結構進行疲勞裂紋試驗中發現，裂紋的開口位置和擴展方向通常不具有對稱性。如圖4-圖6所示。

圖4 MTS Landmark電液伺服疲勞試驗機系統

圖5 機身蒙皮結構

圖6 7050鋁合金HST645-6高鎖栓連接件

實際疲勞試驗中，對物體施加外載荷，離散粒子的運動狀態可以視為流體運動，在運動過程中存在層流現象，各層粒子以不同的速度向前運動，影響疲勞裂紋的擴展速度和方向。根據牛頓粘性定律對離散模型粒子的初始速度進行了修正，速度分布呈拋物線，其仿真結果如圖7所示。

如圖7所示，在時間步長為675時，由于離散粒子初始速度的降低，孔邊疲勞裂紋并沒有產生，表明疲勞裂紋的萌生時間延后了，在時間步為750時，右側孔邊裂紋開始萌發并擴展，時間步為825時，雙孔的疲勞裂紋都已經產生，時間步為1000時，雙孔的疲勞裂紋連通。根據該仿真結果與實際的疲勞裂紋圖片對比可見，兩者之間具有較高的相符度，證明了該方法在處理疲勞裂紋演化問題的優勢。

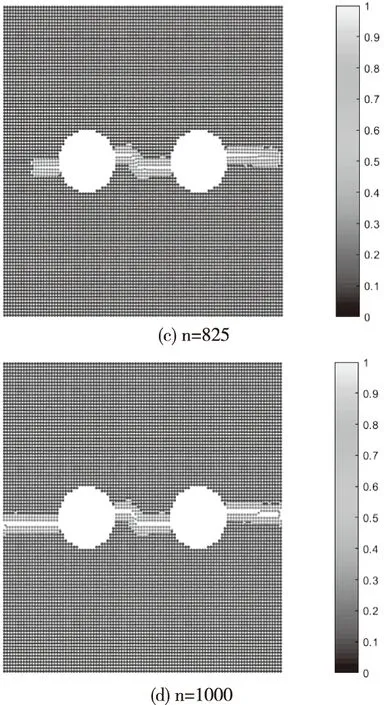
圖7 基于PD的修正雙孔裂紋模擬

3.2 基于擴展有限元方法的裂紋擴展模擬

采用傳統方法中的擴展有限元方法對裂紋演化進行了模擬，其結果如圖8所示:

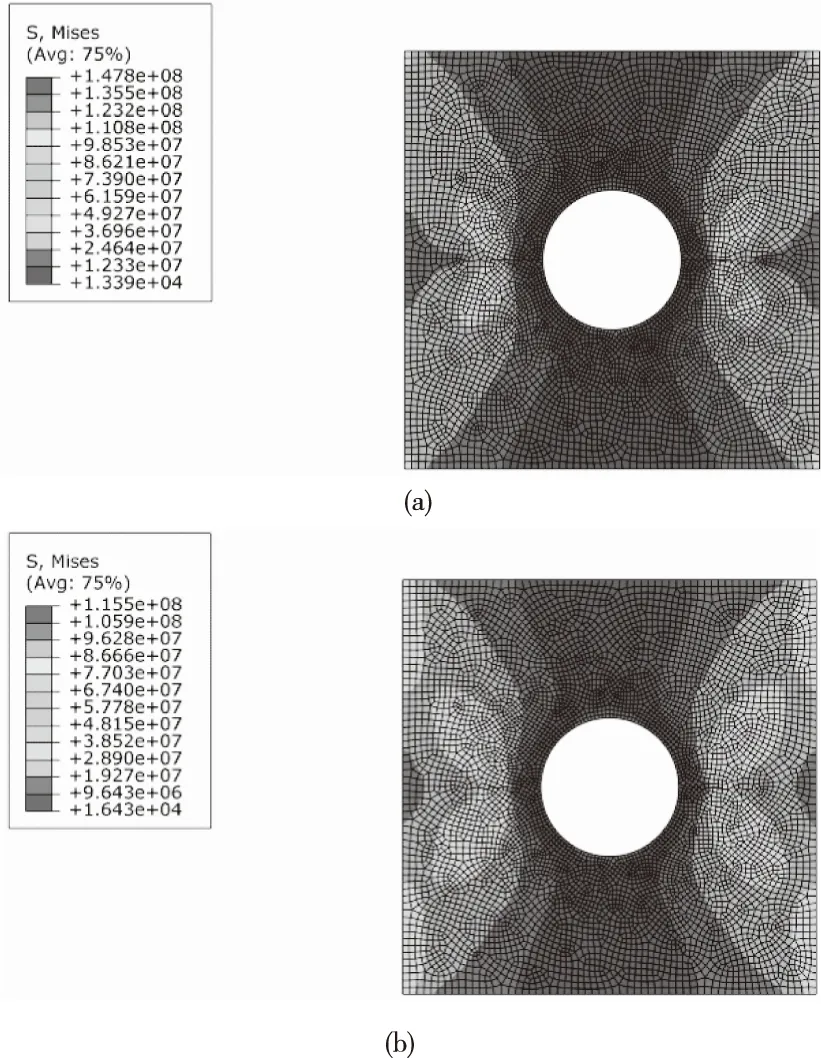
圖8 基于XFEM的單孔裂紋模擬

通過上圖可知，擴展有限元法可以用于單孔裂紋演化過程的模擬，但是其仍需進行網格劃分，對網格具有較強的依賴性，且該方法基于連續性假設，并不能很好地解釋應力尖端的奇異性，自然也不能考慮尖端應力強度因子之間的干涉作用。因此，該方法在雙孔裂紋演化模擬上的應用有待進一步研究。

4 結論與展望

毗域動力學方法提供了一種積分的思想，從非局部的觀點來重新定義裂縫的萌生，生長和擴展，較好地解釋了應力尖端的奇異性，對裂紋路徑形狀、分支模式和傳播速度有較好的預測能力，解決了連續介質力學在遇到含裂紋的材料時，方程求解困難的問題。該方法摒棄了物體變形時仍保持連續性的基本假設，對連續性進行了非局部新定義，以微觀粒子間作用力的表現形式將局部和非局部思想統一在一個體系下。相較于有限元方法，其數值求解過程是一種無網格法，能較好地自發模擬裂紋演變過程。本文建立了航空連接結構裂紋演變問題的非局部模型，結合實際疲勞試驗對PD模型進行了修正，并將毗域動力學方法與擴展有限元方法進行了對比，算例表現了毗域動力學方法在處理不連續區域時的優勢，避免了有限元法的網格依賴性，從微觀粒子角度解釋了應力尖端的奇異性，與實際疲勞試驗具有較高的相符度。該方法可應用于航空故障診斷與預測，將可推廣應用在缺陷、相變、位錯等其它需要考慮材料內部作用的復雜問題，為非局部問題提供新的解決方法。非均勻材料的離散化問題有待進一步研究。