光伏并網逆變器LCL濾波器參數設計方法
孔令霞,王維慶,王海云
(新疆大學電氣工程學院,新疆 烏魯木齊市 830047)
1 引言
隨著化石能源的短缺,太陽能和風能等可再生能源的利用得到了廣泛關注[1],而以光伏發電為代表的發電方式是清潔能源發電的重要組成部分。在新能源發電并網系統中,濾波器是連接并網逆變器和電網的重要元件。LCL濾波器因其濾波性能好,開關損耗小,成本低,體積小等優點而被廣泛應用于光伏并網逆變系統[2-4]。LCL濾波器參數設計合理與否,直接影響濾波效果、濾波器體積和電網的穩定性。新能源并網逆變系統對并網點處的入網電流有嚴格的并網標準,故LCL濾波器參數設計是否有效可依據并網點處的入網電流是否滿足并網要求來判斷[5]。其中并網點處電流總諧波畸變率(total harmonic distortion,THD)是衡量并網電流是否滿足并網要求的重要指標[6-7]。而LCL濾波器的參數設計過程比較復雜,這也使得其參數設計成為研究熱點[8]。
為了節約LCL濾波器的成本,減小其體積,文獻[9]所提的LCL濾波器參數設計方法通過分析逆變器側諧波產生的原因,計算各次諧波,并建立THD估算模型,期望以并網電流的諧波畸變率為目標設計濾波器各參數值,該方法沒有嚴密的數學推導,且多依賴于經驗,對實際工程中LCL光伏并網濾波器的設計可借鑒性不強。文獻[10]所提方法從LCL濾波器逆變器側電流紋波產生機理出發,推導出逆變器側電感計算公式,再根據入網電流質量要求的各次諧波的限制指標以及網側電感和電容器儲能最小為目標,確定網側電感和濾波電容的參數值,然后通過硬性約束條件反復校驗和修正才能得到理想的各參數值。該方法復雜,在實際工程中不便實現。文獻[11]中的方法通過電流紋波衰減率來計算網側電感值,并通過無功吸收比來設計濾波電容。雖然對于各參數設計來說,該方法有嚴密的數學公式推導,但沒有考慮LCL濾波器總電感壓降約束條件,使得設計的濾波器總電感壓降較大,影響并網系統電壓質量。文獻[12-13]提出了一種圖解法來設計LCL濾波器各參數,此方法能直觀反應各參數之間的相互關系,從而確定濾波器各參數值。該方法局限在于,若某一參數變化,其它參數相應變化,故增加了濾波器設計的復雜程度,且該方法沒考慮各種優化目標,所以其設計結果不一定最優。文獻[14]提出一種基于遺傳算法的LCL濾波器參數優化方法,其優化目標包含了紋波電流最小化、功率損耗最小化和諧波衰減最大化,但并沒有考慮總電感值最小化,電感比例系數最小化等優化目標,故具有一定局限性。
對于上述LCL濾波器設計方法存在的不足,同時為保證并網電流滿足要求且LCL濾波器滿足多個優化目標,在傳統圖解法的基礎上,提出一種LCL濾波器參數設計方法。所提方法從LCL濾波器逆變器側電流、網側電流與逆變器側電壓的傳遞函數的伯德圖為切入點,分析其濾波性能,然后分析逆變器側電流、網側電流與電感比例系數及電容的關系,再根據LCL濾波器設計要求、電網硬性約束條件,確定各參數的大致范圍。最后以紋波電流小、諧波衰減性能好、總電感值小、阻尼電阻功率損耗小和電感比例系數小為目標設計目標函數,通過灰狼算法確定各濾波器參數最優值,并在Matlab仿真平臺搭建仿真模型,驗證所提設計方法的有效性。
2 光伏并網逆變系統分析
2.1 三相光伏并網逆變系統電路拓撲結構
采用LCL型并網濾波器的三相光伏并網逆變系統主電路拓撲結構如圖1所示。
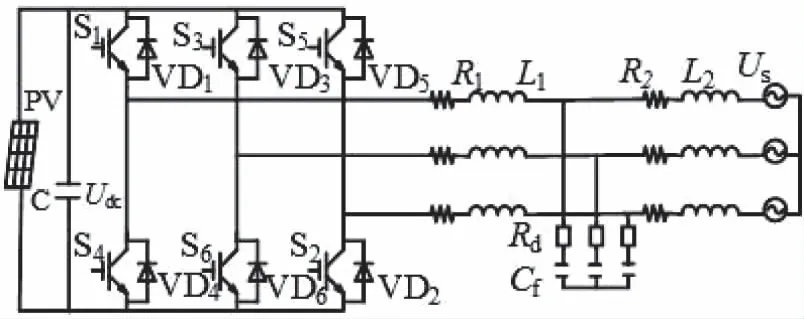
圖1 三相光伏并網系統拓撲圖
圖中PV為光伏陣列,C為直流穩壓電容,S1-S6為6個IGBT晶體管開關,VD1-VD6為續流二極管,R1是逆變器側電感L1的內阻和開關管損耗的等效電阻,R2是逆變器側電感L2的等效內阻,Cf是濾波電容,Rd為濾波電容支路阻尼電阻,Udc為穩壓電容端電壓,Us為電網電壓。
2.2 LCL濾波器特性分析
2.2.1LCL濾波器數學模型
并網逆變器側輸出電壓由基波電壓和諧波電壓兩部分組成。R1和R2很小可忽略,故LCL濾波器在并網模式下的諧波電源等效數學模型如圖2所示。
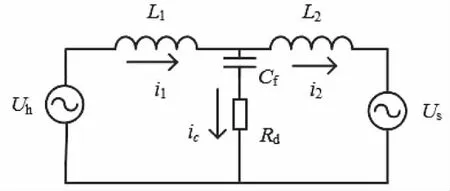
圖2 LCL濾波器并網模式下諧波等效模型
上圖中,Uh為諧波電壓源電壓,i1是逆變器側輸出電流,i2是網側電流,Us為電網電壓。則可得i1與Uh的傳遞函數,如式(1)所示
(1)
利用Matlab繪制出有阻尼型LCL濾波器、L1型和L1+L2型濾波器傳遞函數Y11(s)的Bode圖,如圖3所示。

圖3 濾波器Y11(s)伯德圖
由上圖可知,對逆變器側電流i1來說,在低于諧振頻率時,LCL型濾波器的濾波效果和單L1+L2型濾波器相近,而在高于諧振頻率時,LCL型濾波器的濾波效果和單L1型濾波器相近。
2.2.2 逆變器側電流與電感比例系數和濾波電容關系
將s=jhω帶入式(1)(h為諧波次數,ω為電網基波角頻率)可得LCL型濾波器逆變器側電流i1與Uh的幅值關系,如式(2)所示
(2)
式中:A(jhω)和B(jhω)分別如式(3)和(4)所示
A(jhω)=1-h2ω2L2Cf+jhωRdCf
(3)
B(jhω)=h2ω2RdCf(L1+L2)-jhω(L1+L2)+h3ω3L1L2Cf
(4)
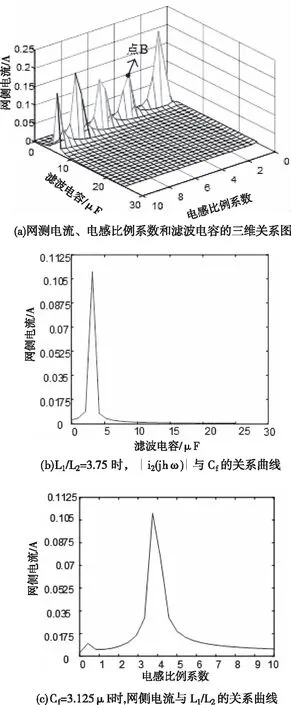
假設開關頻率fsw為10kHz,取開關頻率處(即h=200)諧波電壓源,可得逆變器側電流∣i1(jhω)∣、電感比例系數L1/L2和濾波電容Cf的三維坐標關系圖,如圖4(a)所示。從圖中可以看出,A點附近的諧波電流、電感比例系數和電容取值都比較小。A點坐標為(3.75,3.125,0.1875),取L1/L2=3.75,可得∣i1(jhω)∣與Cf的關系曲線,如圖4(b)所示。再取Cf=3.125μF,可得逆變器側電流與L1/L2的關系曲線,如圖4(c)所示。
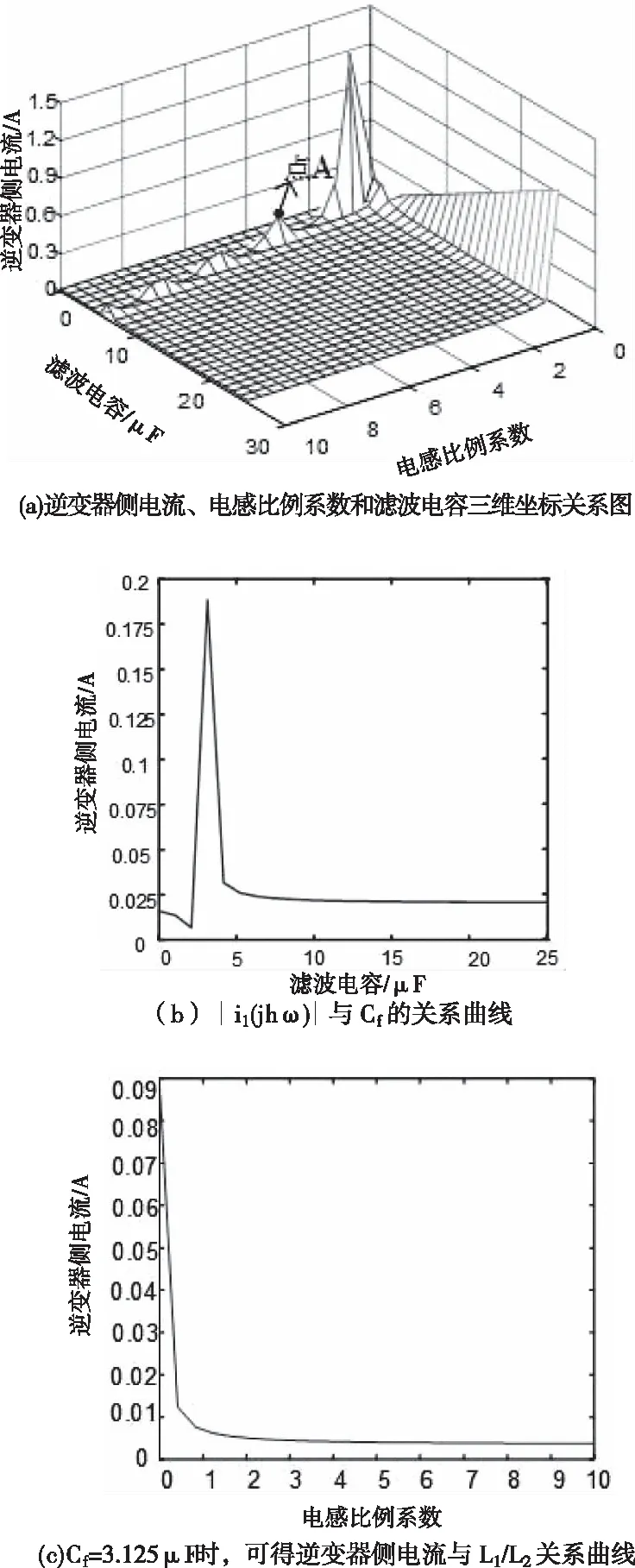
圖4 逆變器側電流幅值與L1/L2和Cf關系圖
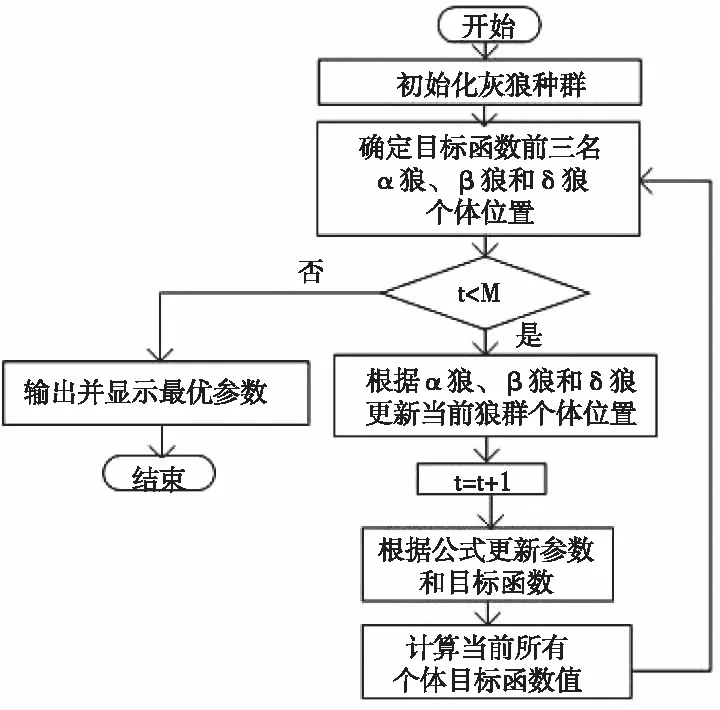
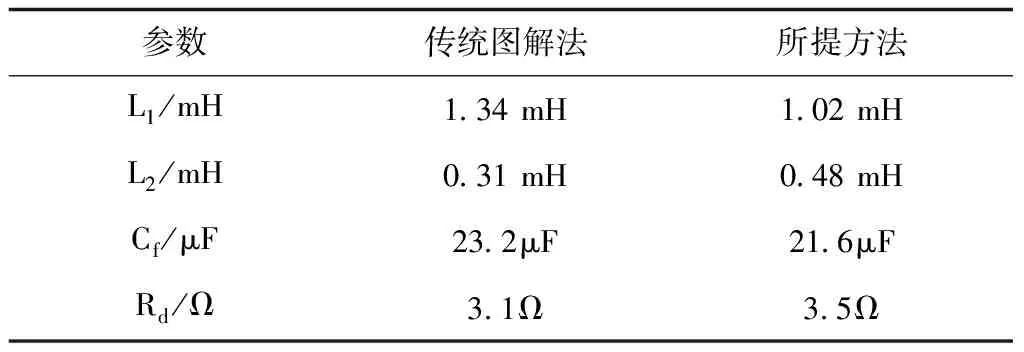
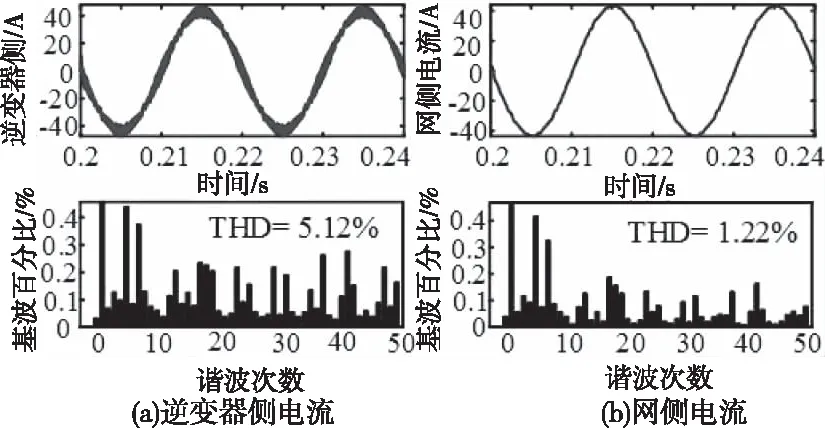
由圖4(b)可知,電感比例系數一定的情況下,紋波電流的幅值與電容的關系曲線是一條線在0 2.2.3 網側電流與電感比例系數及電容關系 由圖2可得有阻尼型LCL濾波器網側電流i2和逆變器側電壓Uh之間的傳遞函數,如式(5)所示 (5) 對于L1+L2型濾波器來說,其網側電流和逆變器側電壓之間的傳遞函數如式(6)所示 (6) 利用Matlab繪制出L1+L2型濾波器、有阻尼和無阻尼型LCL濾波器傳遞函數Y21(s)的Bode圖,如圖5所示。 圖5 濾波器Y21(s)伯德圖 由上圖可知,對于網測電流i2來說,在低于諧振頻率時,LCL型濾波器和L1+L2型濾波器的濾波效果相近,而高于諧振頻率時,LCL型濾波器幅頻衰減特性斜率明顯優于L1+L2型濾波器。而相較于無阻尼LCL型濾波器,有阻尼型LCL濾波器有效抑制了諧振峰。 將s=jhω帶入式(3),可得有阻尼型LCL濾波器網側電流和逆變器側電壓的幅值關系,如式(7)所示 (7) 式中:C(jhω)如式(8)所示,B(jhω)如式(4)所示 C(jhω)=1+jhωRdCf (8) 由此可畫出網測電流∣i2(jhω)∣、電感比例系數L1/L2和濾波電容Cf的三維關系圖,如圖6(a)所示。從圖6(a)可看出,相比于圖4(a),經LCL濾波器后,諧波電流幅值有明顯減小。圖6(a)中B點是圖4(a)中點A的對應點,其坐標為(3.75,3.125,0.1085)。取L1/L2=3.75,可得∣i2(jhω)∣與Cf的關系曲線,如圖6(b)所示。再取Cf=3.125μF,可得網側電流與L1/L2的關系曲線,如圖6(c)所示。 圖6 網測電流幅值與L1/L2和Cf關系圖 圖6(b)與圖4(b)的變化趨勢及其變化原理一致,這里不再贅述。由圖6(c)可知,在濾波電容一定的條件下,網測諧波電流幅值與L1/L2的關系圖是一條先緩慢增加,再急劇增加,然后急劇下降,最后趨于平穩的曲線。即當電感比例系數在4附近時,諧振頻率與開關頻率重合。故在滿足濾波效果的情況下,電感比例系數應在合適范圍內取值。 LCL濾波器各參數的設計應結合系統參數,綜合考慮各方面的因素,才能使設計的LCL濾波器參數有效可行。綜合文獻[9-14],LCL濾波器參數設計應滿足以下約束條件。 3.1.1 總電感值約束條件 對于LCL濾波器來說,總電感值越大,其濾波效果越好,但是濾波器的體積也越大,成本也越高,對系統的動態響應影響也越大。綜合考慮以上因素,可根據總電感壓降約束條件確定總電感值的上限,如式(9)所示。 (9) 其中Us為電網線電壓有效值,P為逆變器輸出有功功率,ω是電網角頻率。 3.1.2 逆變器側電感L1下限約束條件 隨著L1的增加,濾波器的成本呈指數增長。所以在滿足并網電流要求的情況下,逆變器側電感L1越小越好。而最大允許紋波電流對電感L1的造價和重量影響很大,過大的電流紋波會增加功率模塊的容量,這意味著損耗、溫升和電感L1成本和體積的增加。所以在設計L1時應考慮紋波電流的影響。所提方法采用三電平SPWM調制方式,紋波電流計算公式如式(10)所示 (10) 其中,Ts是開關周期,Udc是穩壓電容端電壓,M是調制比。通過式(14)找出最大紋波電流Δimax,則電感L1的下限可由式(11)確定,其公式如下 (11) 其中fsw為開關頻率。 3.1.3 諧振頻率約束條件 LCL濾波器參數設計時,諧振頻率的選擇以滿足諧波衰減的需求為主,為了提高對高次諧波(開關及其倍頻次諧波)和低次諧波的抑制效果,諧振頻率應低于最小的主導低頻邊帶諧波,故對LCL濾波器的諧振頻率fres有如下要求 (12) 式中,f1是電網基波頻率。 3.1.4 濾波電容約束條件 濾波電容Cf越大,從濾波電容支路流過的高頻諧波分量越多,但濾波電容過大,其吸收的無功功率越多,會降低電網的功率因數。故為了保證并網系統的高功率因數,濾波電容Cf吸收的無功功率不應高于系統額定功率的5%,其約束條件如式(13)所示 (13) 其中,P為系統額定輸出有功,Em為相電壓有效值。 傳統圖解法所設計的LCL濾波器參數只考慮了濾波效果,沒有綜合考慮相應的優化目標,故具有一定局限性。而所提方法在傳統圖解法的基礎上考慮了五個優化目標,即紋波電流最小化、諧波衰減最大化、總電感值最小化、功率損耗最小化、電感比例系數最小化,并建立如下目標函數。 minf(x)=ω1f1+ω2f2+ω3f3+ω4f4+ω5f5 (14) 其中子目標函數minf1表示最小紋波電流,如式(15)所示;minf2表示最小紋波衰減比值λ,如式(16)所示;minf3表示LCL濾波器總電感值之和LT=L1+L2最小;minf4表示功率損耗Ploss最小,如式(17)所示(ω為電網基波角頻率,Ui為逆變器輸出電壓);minf5表示電感比例系數L1/L2最小。 (15) (16) (17) 依據熵值權重法[14]可確定每個子目標的權重系數ωi,將其帶入式(14)則可得線性加權后的目標函數,如式(18)所示: minf(x)=0.1660△imax+0.1757λ+ (18) 其中λ為諧波衰減比值,如式(11)所示。 灰狼算法因其結構簡單、控制參數少、易于操作和全局搜索能力強等特點被廣泛應用于參數優化領域,故本文用灰狼算法確定LCL濾波器各參數值。 在灰狼算法中,通過式(19)確定各組狼與獵物(最優解)的距離,在根據式(20)更新狼群位置 D=|C*Xp(t)-X(t)| (19) X(t+1)=Xp(t)-A*D (20) 其中,D代表第t次迭代時灰狼個體與獵物的距離,Xp(t)表示第t次迭代時獵物的位置,X(t)表示第t次迭代時灰狼個體的位置,C為擺動因子,A為收斂因子。 狼群中的普通狼(ω狼)根據式(21)確定自己與前三名α、β和δ狼的距離,然后通過式(22)更新各自的位置,最后根據式(23)對獵物進行定位,判斷出個體向獵物移動的方向,再由α狼帶領β、δ和ω狼逐漸向獵物靠近并包圍獵物。灰狼算法的流程圖如圖(7)所示。 圖7 灰狼算法流程圖 (21) (22) Xp(t+1)=(X1+X2+X3)/3 (23) S1)設置變量X=[L1,L2,Cf,Rd],根據濾波器設計要求和約束條件,確定各參數取值上下界。取狼群的大小為N、最大迭代次數為M,并初始化灰狼種群。 S2)根據求解目標計算每只狼的適應度值,并選擇排名前三的狼個體依次賦予Xα、Xβ和Xδ。 S3)由Xα、Xβ和Xδ,通過狼群包圍和狼群捕獵的步驟,可根據式(21)可計算出其它灰狼與α、β和δ狼之間的距離。 S4)根據式(22)和式(23)向占據最優位置的成員移動,優化狼群中每只狼的位置。 S5)在更新后的α、β和δ狼中,把適應度最高的灰狼與目標函數做對比,然后進行位置更新和目標函數更新,確定最優解。 S6)判斷迭代次數是否達到預設最大迭代次數,達到最大迭代次數則輸出最優解,否則轉步驟S2。 為提高算法精確,得到最優解,取灰狼種群規模為N=100,最大迭代次數M=200,根據圖4、圖6和式(17)給各參數變量賦合適初值。 為說明所提方法的優越性,給出同樣條件下傳統圖解法設計的LCL濾波器參數和所提方法設計的LCL濾波器參數,如表(1)所示。 為驗證所LCL濾波器參數設計方法的可靠性和優越性,按兩種方案所設計的LCL濾波器參數值(見表1)分別在Matlab/simulink平臺搭建光伏并網逆變系統仿真模型。并網逆變系統參數設置如下:系統額定功率為15kW,交流線電壓有效值為380V,直流電壓為700V,電網頻率為50Hz,逆變器開關頻率為10kHz。 表1 兩種方案下的參數設計結果 傳統圖解法設計的LCL濾波器對應的逆變器側電流i1和網測電流i2波形及其對應頻譜圖如圖8(a)、(b)所示。本文所提方法設計的LCL濾波器對應的逆變器側電流i1和網側電流i2波形及其對應頻譜圖如圖9(a)、(b)所示。 圖8 傳統圖解法A相電流波形及其頻譜分析 圖9 所提設計方法A相電流波形及其頻譜分析 由圖8和圖9可知,采用傳統圖解法設計的LCL濾波器時,并網逆變器側電流TDH=5.12%,網側電流TDH=1.22%,經濾波器濾波,諧波TDH降低了3.9%。而采用所提方法設計的LCL濾波器時,并網逆變器側電流TDH=4.89%,網側電流TDH=0.86%,諧波TDH降低了4.03%。 對兩者進行對比可知,用文中方法設計的LCL濾波器的諧波衰減性能優于用傳統圖解法設計的LCL濾波器,且采用所提方法設計的LCL濾波器的并網系統的電流質量更好。 通過對并網逆變系統LCL濾波器的傳遞函數進行分析,根據濾波器設計要求采用灰狼算法對濾波器參數進行優化,把參數設計結果和光伏并網逆變系統仿真結果進行對比,可得出如下結論: 1)與傳統圖解法相比,所提LCL濾波器參數設計方法的總電感值更小,且逆變器側電感和濾波電容也更小,但阻尼電阻略大,總體說來所提設計方法設計的濾波器成本更低。 2)仿真結果表明,提出的LCL濾波器設計方法的TDH下降更顯著,其諧波衰減性能優于用傳統圖解法設計的LCL濾波器。 3)相比于傳統圖解法,采用所提方法設計的LCL濾波器的逆變器側和網側的諧波電流更小,意味著其溫升和損耗也更小,并網電流質量更高。 總體說來,所提方法設計的光伏并網LCL濾波器濾波效果良好且較為經濟,說明此參數設計方法有效可行,對實際工程中LCL型光伏并網濾波器的設計有可借鑒性。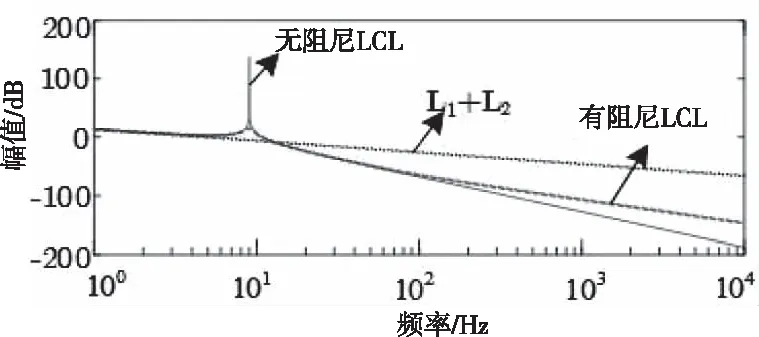
3 LCL型濾波器的參數優化設計
3.1 LCL濾波器參數設計約束條件
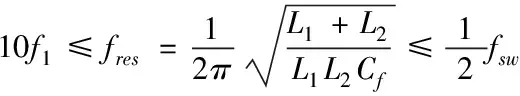
3.2 優化目標
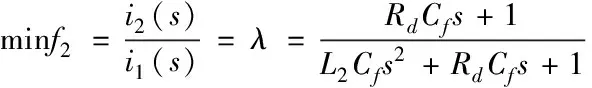
4 LCL濾波器參數灰狼算法優化方法
4.1 目標函數
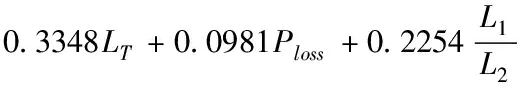
4.2 灰狼算法優化過程
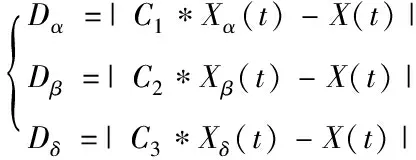
4.3 算法優化結果
5 仿真及結果分析

6 結論

