基于CEEMDAN-SAFA-LSSVM的短期風功率預測

張景楊，王維慶，王海云，武家輝

(新疆大學可再生能源發電與并網技術教育部工程研究中心，新疆烏魯木齊830047)

1 引言

由于風功率具有隨機性大，波動性強的缺點，風電的大規模使用給電網的安全穩定運行帶來了很大的風險[1]。因此對風功率的精準預測是保證電網安全穩定運行的前提[2]。

目前，對風功率預測有許多方法，例如，時間序列法的優點是易于建模，但在描述風功率變化特征時存在缺點[3]；卡爾曼濾波模型對風功率進行預測尋優時雖然可以避免陷入局部最優，但該方法易受統計特性不明的影響[4]；相關向量機雖然消除了卡爾曼模型易受統計特性不明的影響，但該方法需要訓練大量的原始數據作為輸入[5-6]；EMD與SVM組合預測模型雖然有著較高的預測精度，但該模型的缺點是復雜度高和訓練時間長[7-9]。

通過上述分析，本文采用CEEMDAN算法對風功率進行分解能夠很好地克服EMD和EEMD所存在的問題，在分解風功率序列上有更好的表現[10]。同時對于向量機(SupportVectorMachine，SVM)模型的缺點，提出一種螢火蟲(SAFA)優化最小二乘支持向量機(LSSVM)預測模型[11]。可以解決LSSVM預測精度易受參數選擇的影響[12]。于是本文建立了一種基于CEEMDAN-SAFA-LSSVM組合預測模型。通過與LSSVM和EEMD-LSSVM進行對比，結果表明本文提出的模型具有更快的收斂速度和更高的預測精度[13]。

2 算法原理

2.1 CEEMDAN算法

CEEMDAN算法是在原始風功率分解過程中的每一階段添加自適應高斯白噪聲，通過計算唯一余量信號得到各個模態分量，分解過程完整，重構誤差極低。有效解決EMD模態混疊問題，同時克服EEMD分解效率低和噪聲難以完全消除的問題[14]。

CEEMDAN算法實現的步驟如下：

1)利用CEEMDAN對信號X(t)+ε0ni(t)進行N次重復分解，通過均值計算得到第一個模態分量

(1)

2)然后對得到的第一個余量信號進行計算r1(t)

(2)

3)然后對信號r1(t)+ε1E1(ni(t))進行N次重復分解，分解完成后可得到第二個模態分量

(3)

4)對于k=2，…，K，計算第k個殘余信號

(4)

5)重復步驟3)的計算過程，得到第k+1個模態函數為

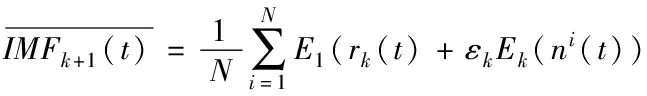
(5)

6)重復計算步驟4)和5)，直到余量信號達到分解的終止條件，最終得到K個模態分量。分解的最終殘差信號為

(6)

最終原始信號可以分解為

(7)

2.2 相空間重構

相空間重構的思想是系統中任一分量都與其它分量有關，而其它分量的信息隱藏在這一分量中。因此，通過對其分量的分析，從而實現重建原非線性系統的目的[15]。

設某一混沌序列的延遲時間為τ，嵌入維數為m，則重構的相空間為

{f(i)=[x(i)，x(i+τ)，x(i+2τ)，…，x(i+(m-1)τ)]}

(8)

式中:f(i)為相點;i=1 2…N。

因此只要τ和m選擇合適，則原系統的狀態空間就和重構的相空間等價。所以，相空間重構要點就是要選取合適的延遲時間τ和嵌入維數m。

3 最小二乘支持向量機及其參數優化

3.1 LSSVM算法

假設m個訓練數據{xi，yi}im=1，xi∈Rn為LSSVM模型的輸入向量，yi∈R為LSSVM模型的輸出向量，則LSSVM數學模型為

(9)

式中：ω—權重，C—懲罰參數，

ξi—松弛變量。

b—偏置。

φ(x)—映射函數。

LSSVM模型的Lagrange函數

(10)

式中：ai——Lagrange乘子。

式(9)求偏導，消去ω和ξi，可得到LSSVM模型的估計公式為

(11)

式中：K(x，xi)——核函數。

本文核函數采用徑向基核函數，其定義為

(12)

式中：g——核函數的參數。

3.2 螢火蟲算法

螢火蟲算法(FireflyAlgorithm，FA)是通過高亮度的螢火蟲會吸引低亮度的螢火蟲，可以使螢火蟲不斷變換位置，從而實現參數尋優的目的[15]。

亮度高的螢火蟲j會吸引亮度低的螢火蟲i，螢火蟲位置變化公式如下

Xi=Xi+β(r)×(Xj-Xi)+α×εi

(13)

式中：β(r)——螢火蟲之間的吸引度。

(14)

β0——rij=0時螢火蟲的吸引度；

Xi——螢火蟲i的位置。

Xj——螢火蟲j的位置。

為提高FA算法的搜索能力，將非線性動態慣性W引入式(15)，得到新的螢火蟲位置更新式(16)

(15)

式中：wmax——權重w的最大值；

wmin——權重w的最小值；

f——當前螢火蟲的適應度函數值；

favg——所有螢火蟲個體的平均適應度函數值；

fmin——螢火蟲的最小適應度函數值。

所以，式(13)改進為

Xi=w×Xi+β(r)×(Xj-Xi)+α×εi

(16)

3.3 SAFA優化LSSVM的實現

針對LSSVM的預測精度受參數選擇的影響，將SAFA引入用于對LSSVM的參數優化，可以解決LSSVM預測精度受參數選擇的影響，從而可以提高LSSVM對風功率的預測精度，同時本文采用均方差作為適應度函數如下式

(17)

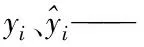
[Cmin，Cmax]——C的取值范圍。

[gmin，gmax]——g的取值范圍。

3.4 SAFA優化LSSVM的優化流程

由于SAFA算法對種群中最亮螢火蟲的位置具有快速準確的尋優，同時又因為LSSVM模型的預測精度易受懲罰參數C和核函數參數g的影響，所以SAFA優化LSSVM就是其將參數(C，g)最優化問題轉換成尋找螢火蟲群體中螢火蟲亮度最大的問題，即尋找到螢火蟲亮度最大的位置(C*，g*)。基于SAFA-LSSVM的風功率預測步驟具體可描述如下。

Step1：設置SAFA的初始參數；螢火蟲個數N，步長α，最大迭代次數T、初始吸引度β0、螢火蟲初始位置X。

Step2：根據計算得到所有螢火蟲的亮度再根據螢火蟲的亮度大小對其進行排序，計算所有螢火蟲群體的適應度函數值fi(C，g)并對其進行排序，得到最亮螢火蟲的位置。

Step3：判斷是否達到最大迭代次數，若大于最大迭代次數T，則轉到Step4，反之轉到Step5。

Step4：找到最亮螢火蟲位置，從而可以得到優化后的LSSVM模型的參數(C*，g*)。

Step5：重新確定螢火蟲位置，根據式(16)確定螢火蟲最新的位置。

SAFA優化LSSVM的流程圖如圖1所示。

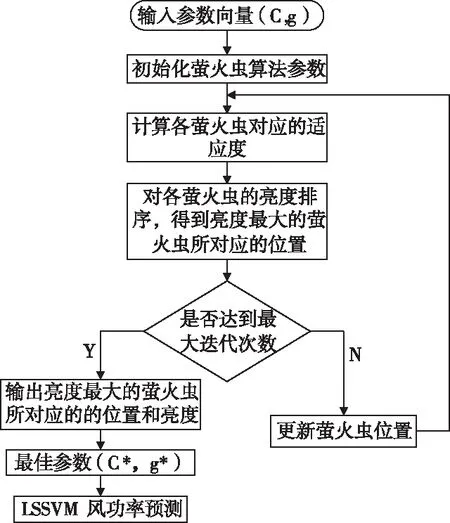
圖1 SAFA優化LSSVM的流程圖

4 基于CEEMDAN-SAFA-LSSVM風功率短期組合預測方法

CEEMDAN算法是在原始風功率分解過程中的每一階段添加自適應高斯白噪聲，通過計算得到各個特征相異的分量，分解過程完整，重構誤差極低。有效解決EMD模態混疊問題，同時克服EEMD分解效率低和噪聲難以完全消除的問題，然后利用相空間重構原理，對IMF分量進行重構，可有效提高風功率預測精度和預測效率。LSSVM在預測方面優于SVM但預測精度易受參數的選擇影響，所以提出SAFA對LSSVM參數進行優化，可有效解決LSSVM預測精度受參數選擇的影響。基于此建立了CEEMDAN-SAFA-LSSVM的組合預測模型對風功進行預測，預測流程如圖2所示。

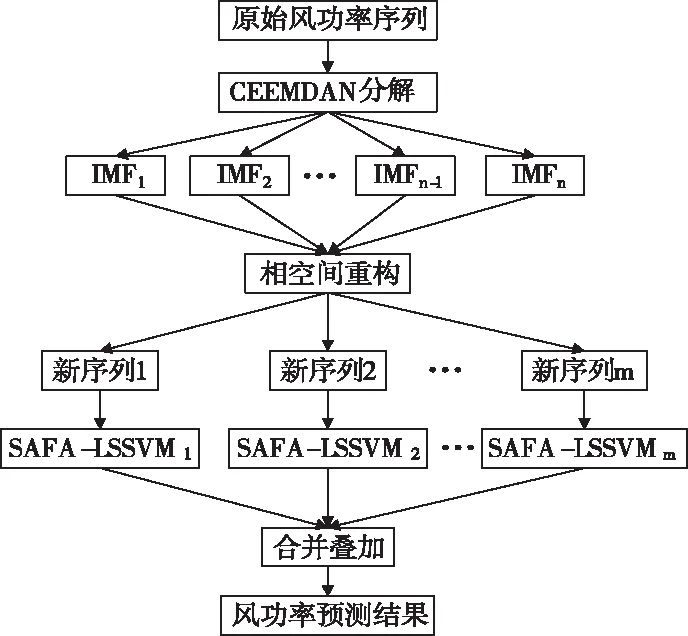
圖2 CEEMDAN-SAFA-LSSVM預測流程

CEEMDAN-SAFA-LSSVM模型實施步驟如下。

1)采用 CEEMDAN算法對風功率進行分解，將其分解成各個特征相異的各個分量。

2)對風功率序列分解產生的各個分量進行相空間重構來確定各分量的參數τ和m。

3)根據新本征模態分量的特征，使用SAFA優化后的LSSVM模型，對各新本征模態分量分別進行預測。

4)將各分量的預測結果進行疊加處理，從而可以得到真實的預測結果。

5 算例分析

為了證明本文所提CEEMDAN-SAFA-LSSVM預測模型的有效性，以中國新疆某風電場實測風功率數據為測試樣本，每隔15min取一個點，以某月連續12d的1152個數據為測試樣本，用前1088個數據為本文模型的初始訓練數據，后64個數據用來作為預測模型的測試值來驗證模型的有效性。

5.1 CEEMDAN對風功率序列的分解

CEEMDAN算法是在原始風功率分解的每一階段添加自適應高斯白噪聲，通過計算可將原始風功率分解成多個模態分量，分解過程完整，誤差極低。解決了EMD和EEMD中存在的模態混疊問題，計算量過大和添加白噪聲幅值不當的問題。CEEMDAN對原始風功率序列進行分解如圖3所示。

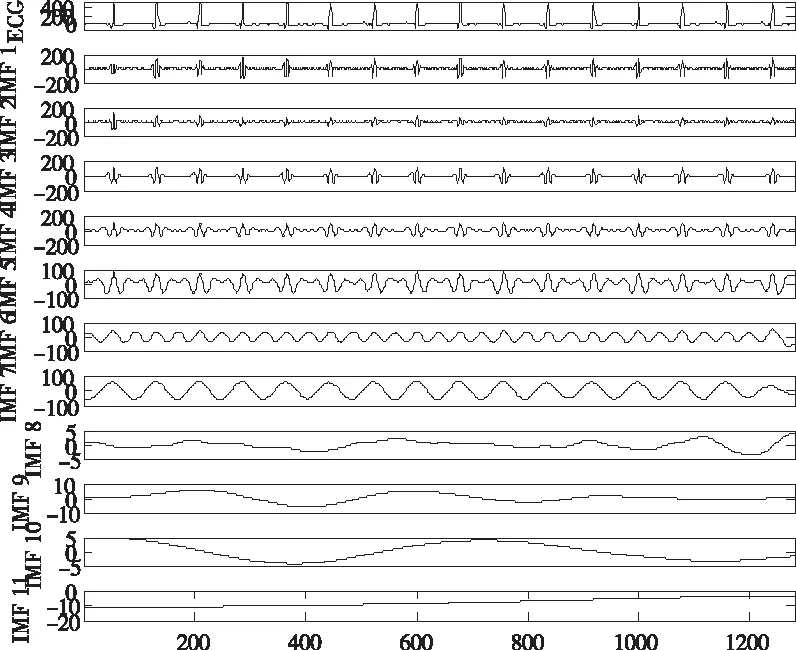
圖3 CEEMDAN分解的風功率序列

從圖3可知，原始風功率序列被分解成了特征互異的11個IMF分量和一個ECG分量。然后利用相空間重構原理對經CEEMDAN分解后的每個IMF分量進行處理，同時確定每個分量的延遲時間和嵌入維數。表1給出了各個IMF分量經相空間重構后確定的延遲時間τ和嵌入維數m[16-17]。

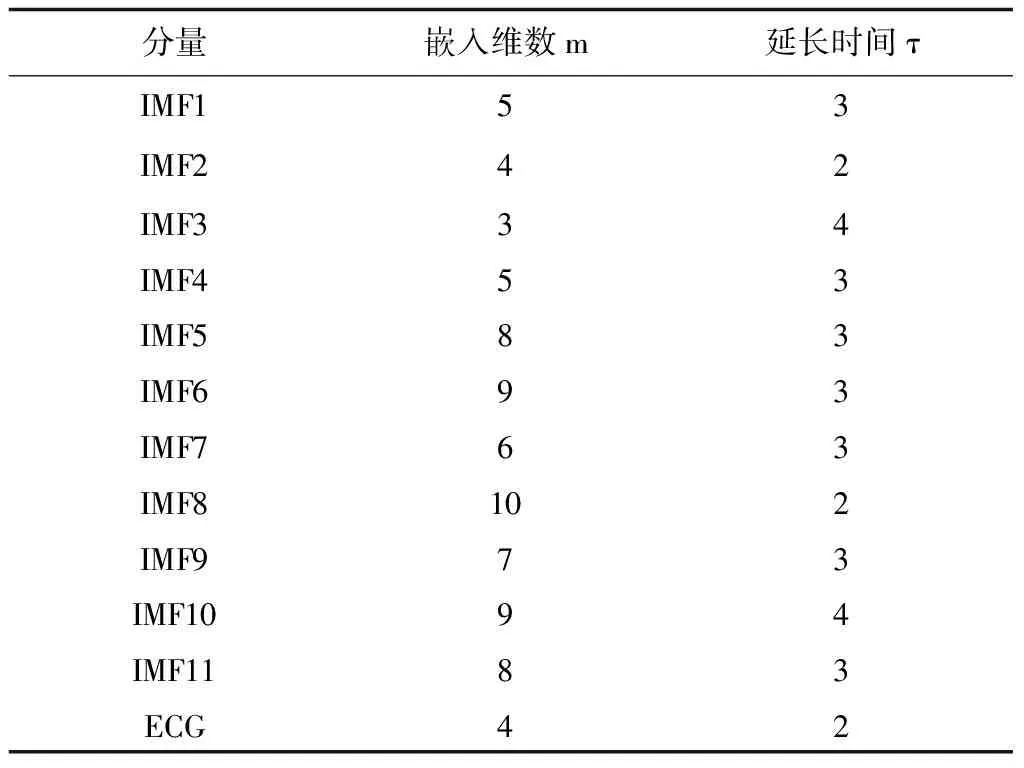
表1 相空間重構參數

對CEEMDAN分解后的各個分量進行相空間重構，然后對重構之后的各分量分別建立的SAFA-LSSVM預測模型，對風功率進行預測，最后對預測結果進行疊加得到實際的預測結果。

為了驗證本文所用模型對于參數優化的優越性，將本文模型與LSSVM，EEMD-LSSVM進行對比。

由圖4可見，CEEMDAN-SAFA-LSSVM優化模型數時，其迭代次數最少，10次左右就能達到收斂，而LSSVM和EEMD-LSSVM需迭代20次左右才可實現收斂，雖然本文的模型收斂時的適應度稍微大些，但本文的模型整體效果更為理想。

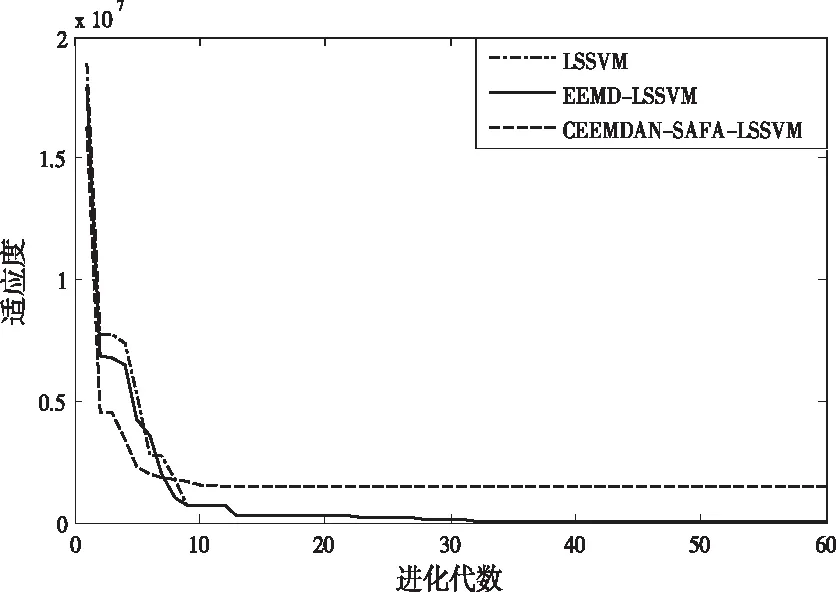
圖4 三種優化算法的適應度曲線

5.2 預測結果對比分析

為提高風功率預測的效率，采用滾動預測法對后64個數據點進行滾動預測，然后將其預測的各分量的結果進行疊加得到風功率最終預測值。為驗證CEEMDAN-SAFA-LSSVM組合預測模型相比于其它模型的優越性，與LSSM、EEMD-LSSVM進行對比，結果如圖5所示。

圖5 風功率預測曲線

從圖5可知，雖然LSSVM與EEMD-LSSV兩種預測模型預測出的風功率在整體趨勢上大致可以跟隨實際輸出，但是在關鍵點處這兩種預測模型的預測曲線偏離實際輸出較大，預測效果較差。而本文提出的CEEMDA-SAFA-LSSVM預測模型在大多數預測點都更貼近實際值，預測效果比LSSVM和EEMD-LSSVM這兩種模型更好，同時在關鍵點本文預測模型的預測曲線能緊跟實際風功率序列的變化。說明，本文模型預測效果更好。

為了比較每個預測方法的預測精度，選用絕對百分比誤差(MAPE)和均方根誤差(RMSE)這兩個參數對各方法進行評價。

(18)

(19)

從表2可知，相比于LSSVM，EEMD-LSSVM預測模型的RMSE與MAPE指標分別降低了11.81%和17.44%，預測精度更高，說明對原始風功率進行分解，可以有效提高風功率預測精度。而CEEMD-SAFA-LSSVM模型相對于EEMD-LSSVM模型的RMSE與MAPE指標分別降低了11.61%和13.38%，可知采用CEEMDAN分解法可有效改善EEMD分解中的缺點。同時采用SAFA優化LSSVM參數，提高了LSSVM參數尋優速度和預測的精度。說明本文所提的CEEMDAN-SAFA-LSSVM預測模型提高了風功率預測效率和預測精度。

表2 幾種預測方法結果對比分析

6 結論

本文建立的CEEMDAN-SAFA-LSSVM組合預測模型，對風功率進行短期預測，經過以上分析可得如下結論。

1)利用CEEMDAN對波動的風功率序列進行逐級分解解決了EMD和EEMD中存在的模態混疊問題，計算量過大和添加白噪聲幅值不當的問題。

2)利用相空間重構原理，對IMF分量進行重構，可有效提高風功率預測精度和預測效率。

3)采用SAFA優化LSSVM參數，解決了LSSVM參數尋優效率低的問題。

4)通過與LSSVM和EEMD-LSSVM相比，研究結果表明本文提出的模型CEEMDAN-SAFA-LSSVM降低了原始非平穩序列對預測精度造成的影響提高了收斂速度，同時具有更高的預測精度，證明了本文所提的CEEMDAN-SAFA-LSSVM預測模型對風功率預測的有效性，同時為未來短期風功率預測提供了鋪墊。