Q355矩形截面彈簧卷成形數(shù)值模擬與缺陷分析
項(xiàng)輝宇,周 洋,冷崇杰,魏景輝
(北京工商大學(xué)材料與機(jī)械工程學(xué)院,北京 100048)
1 引言
彈簧種類繁多,在生產(chǎn)生活中應(yīng)用甚廣,它利用動(dòng)能與勢(shì)能的轉(zhuǎn)變實(shí)現(xiàn)控制機(jī)械運(yùn)動(dòng)、吸收或輸出能量等功能。當(dāng)在重載或安裝空間有限的情況下,矩形截面彈簧就可以發(fā)揮它獨(dú)特的優(yōu)勢(shì),與截面為圓形的彈簧相比,相同的尺寸它可以傳遞更大的扭矩[1]。目前,矩形截面彈簧卷制成形通常采用重復(fù)試驗(yàn)的方法[2],這種方式卷制的成功率較低,常常會(huì)伴隨起皺或拉裂等缺陷,如圖1所示,進(jìn)而造成原材料的浪費(fèi),致使彈簧成本居高不下。
隨著計(jì)算技術(shù)的發(fā)展,有限元仿真較試錯(cuò)法的優(yōu)點(diǎn)顯得尤為突出,既可以節(jié)省大量時(shí)間,又可以提高成形質(zhì)量,降低廢品率。國(guó)內(nèi)外學(xué)者對(duì)矩形截面彈簧的學(xué)術(shù)研究為數(shù)不多,李家梅[3]等人對(duì)其設(shè)計(jì)特點(diǎn)進(jìn)行了分析總結(jié),改進(jìn)了濕式盤形彈簧制動(dòng)器中所用的矩形截面彈簧;Jing-Qiu Tang[4]等人設(shè)計(jì)了矩形截面和特殊截面兩種螺旋彈簧,并分別建立了有限元模型,闡述了兩種螺旋彈簧應(yīng)力分布的不同,有利于后續(xù)力學(xué)分析和結(jié)構(gòu)優(yōu)化的研究;日本電氣通訊大學(xué)[5]曾設(shè)計(jì)一款高矩形比彈簧,高加工硬化將實(shí)現(xiàn)高屈服應(yīng)力,不僅實(shí)現(xiàn)了有限元仿真,還在理論分析的基礎(chǔ)上進(jìn)行了相關(guān)實(shí)驗(yàn),并對(duì)彈簧的拉伸、扭轉(zhuǎn)和彎曲特性進(jìn)行了評(píng)價(jià)。
為了提高矩形截面彈簧卷制成形的質(zhì)量,本文針對(duì)拉裂和起皺兩種缺陷建立了質(zhì)量評(píng)價(jià)準(zhǔn)則,并采用MSC.Marc有限元軟件對(duì)其成形過(guò)程進(jìn)行仿真,分別在單因素試驗(yàn)和正交試驗(yàn)的基礎(chǔ)上,分析成形過(guò)程中速度、溫度和摩擦系數(shù)的影響。

2 成形質(zhì)量評(píng)價(jià)準(zhǔn)則的確定
由于在卷制過(guò)程中可能產(chǎn)生外圈拉裂以及內(nèi)圈起皺兩種缺陷,因此,本文針對(duì)這兩種缺陷,以所用金屬材料的塑性成形極限圖為依據(jù),確定矩形截面彈簧卷制成形的質(zhì)量評(píng)價(jià)準(zhǔn)則,并用該準(zhǔn)則對(duì)模擬分析的結(jié)果進(jìn)行評(píng)價(jià)。
2.1 單向拉伸試驗(yàn)
本文試驗(yàn)所用的材料是厚度6mm的Q355鋼板,根據(jù)GB/T228-2002金屬材料拉伸試驗(yàn)室溫試驗(yàn)方法的標(biāo)準(zhǔn)制取比例試樣[6]。在方鋼板上分別沿水平方向,45°方向以及垂直方向進(jìn)行切割為一組拉伸試樣,具體如圖2所示。

圖2 拉伸試驗(yàn)試樣切割方向圖
將通過(guò)線切割機(jī)切割好的一組3個(gè)試樣用拉伸應(yīng)變速率為0.375mm/min的拉伸機(jī)分別進(jìn)行拉伸試驗(yàn)。將通過(guò)拉伸試驗(yàn)所得的工程應(yīng)力和工程應(yīng)變的實(shí)驗(yàn)數(shù)據(jù)轉(zhuǎn)化為真實(shí)應(yīng)力和真實(shí)應(yīng)變數(shù)據(jù),按照計(jì)算數(shù)據(jù)畫(huà)出與軋制方向成0°、45°和90°的三個(gè)試樣的真實(shí)應(yīng)力應(yīng)變曲線,如圖3所示。
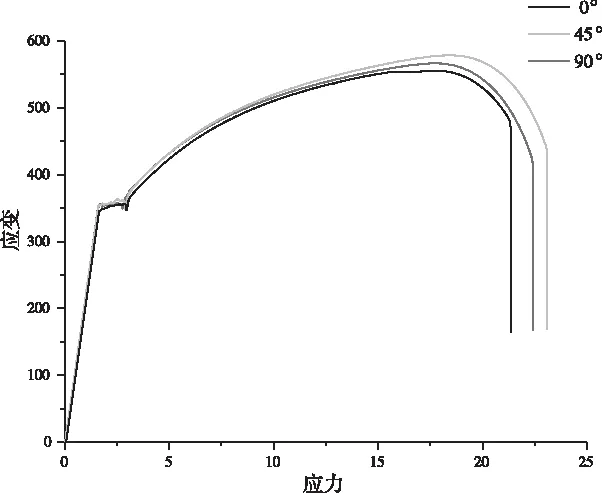
圖3 三個(gè)方向真實(shí)應(yīng)力應(yīng)變曲線
2.2 成形極限圖
金屬材料在彈塑性成形過(guò)程中,極限情況下兩個(gè)主應(yīng)變的對(duì)應(yīng)關(guān)系曲線圖即為成形極限圖(Forming Limit Diagrams,F(xiàn)LD)[7]。針對(duì)矩形截面彈簧卷制過(guò)程的缺陷分析,分為拉裂成形極限和起皺成形極限。目前,Keeler成形極限圖可以作為拉裂成形極限預(yù)測(cè)的參考,它在應(yīng)用時(shí)簡(jiǎn)單方便。Keeler公式如式(1)所示
(1)
拉裂成形極限曲線形狀由下面公式確定

(2)
式(2)已經(jīng)在有限元分析軟件中用來(lái)判斷材料破裂準(zhǔn)則。通過(guò)以上公式,可以發(fā)現(xiàn)由Keeler公式所確定的FLD曲線只與材料的硬化指數(shù)n和方鋼厚度t值兩個(gè)參數(shù)有關(guān),本文中方鋼厚度最小為t=25mm,因此在計(jì)算FLD0時(shí)選用的公式是第三個(gè)t>5.33mm時(shí)的計(jì)算公式。該公式中硬化指數(shù)n可以根據(jù)材料Q355的單向拉伸試驗(yàn)獲得的應(yīng)力應(yīng)變數(shù)據(jù)利用冪指硬化公式進(jìn)行曲線擬合獲得。
真實(shí)應(yīng)力-應(yīng)變曲線可用下列指數(shù)曲線方程表示,即
σ=Kεn
(3)
式中,K—硬化模量;n—硬化指數(shù)。
截取圖3中材料拉伸進(jìn)入塑性形變的部分曲線,應(yīng)用式(3)對(duì)其進(jìn)行擬合,擬合的結(jié)果如圖4所示。
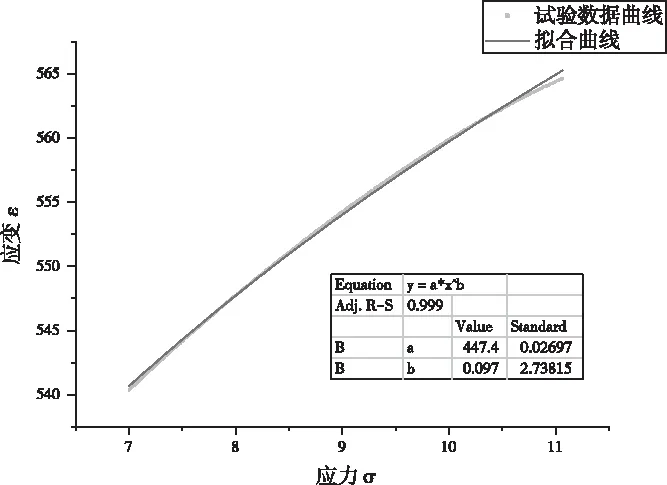
圖4 冪指硬化模型擬合圖
根據(jù)上述參數(shù)的獲得可知t=30mm,n=0.097,這樣可以得到彈簧成形拉裂極限如圖5所示。

圖5 Keeler 成形極限曲線
而對(duì)于起皺成形極限,通常認(rèn)為:當(dāng)εM=-εm時(shí),εt=0,此時(shí)方鋼材料為純剪切的應(yīng)變狀態(tài),以此定義為判斷起皺的準(zhǔn)則。當(dāng)εM<-εm,判定為起皺區(qū)域;當(dāng)εM>-εm,即為非起皺區(qū)域。根據(jù)該準(zhǔn)則可得彈簧成形起皺極限如圖6所示。
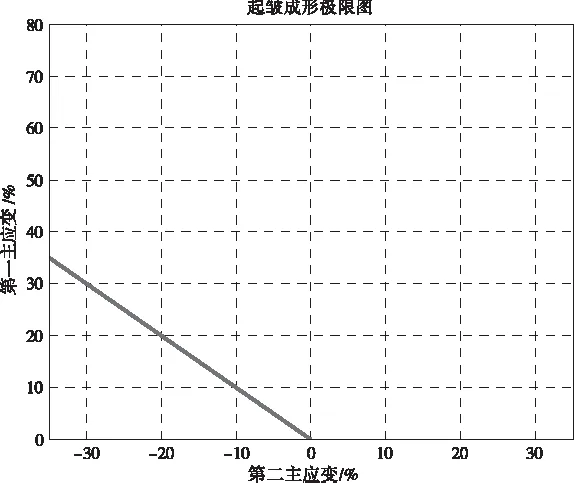
圖6 起皺成形極限曲線
2.3 成形缺陷的預(yù)測(cè)分析
拉裂和起皺的預(yù)測(cè)以成形極限圖為依據(jù)。在設(shè)計(jì)過(guò)程中,分別設(shè)置拉裂成形極限和起皺成形極限的安全閾值,稱為拉裂成形極限臨界曲線和起皺成形極限臨界曲線。在本文中拉裂成形極限的安全閾值取0.1,即在原成形極限的基礎(chǔ)上向下平移0.1個(gè)單位。起皺成形極限的安全閾值取0.5,是將原起皺成形極限直線的斜率變成-1.5。從圖7中可以看出,整個(gè)成形圖分5個(gè)部分,其中在拉裂成形極限曲線之上的部分屬于拉裂區(qū);在拉裂成形極限曲線與其臨界曲線之間的部分屬于拉裂臨界區(qū),位于該部分的節(jié)點(diǎn)有產(chǎn)生拉裂缺陷的趨勢(shì);在兩條臨界曲線之間的部分屬于正常成形區(qū)域;在起皺成形極限臨界曲線與起皺成形極限曲線之間的部分屬起皺臨界區(qū);在起皺成形極限曲線以下的部分屬于起皺區(qū)。

圖7 成形極限安全閾值圖
為了達(dá)到直觀可見(jiàn)的目的,本文以上述材料成形極限曲線為基礎(chǔ),針對(duì)拉裂缺陷和起皺缺陷建立成形質(zhì)量的評(píng)價(jià)準(zhǔn)則,定義為位于非安全區(qū)域模擬單元節(jié)點(diǎn)主應(yīng)變到破裂和起皺臨界曲線的距離的均方差值,如式(4)和式(5)所示
(4)
(5)
式中:n為非安全區(qū)域節(jié)點(diǎn)數(shù)。顯然f、w值越小,彈簧成形質(zhì)量越好,需要注意的是計(jì)算單元節(jié)點(diǎn)均是最終卷制成形產(chǎn)品的單元節(jié)點(diǎn)。
3 矩形截面彈簧有限元模型的建立與仿真
3.1 彈塑性成形基本理論
彈簧卷制過(guò)程分為彈性和塑性兩個(gè)階段,首先在彈性變形階段,其應(yīng)力應(yīng)變關(guān)系由廣義胡克定律確定[8]。
{ε}m=[C]m{σ}m
(6)
式中:{ε}m為應(yīng)變,{σ}m為應(yīng)力,[C]m為彈性矩陣的逆矩陣。
本文選用材料是軋鋼的一種,卷制過(guò)程中大多表現(xiàn)各向異性特點(diǎn),因而應(yīng)用Hill48屈服準(zhǔn)則來(lái)描述矩形截面彈簧卷制成形過(guò)程中的屈服現(xiàn)象,函數(shù)表達(dá)式如式(7)所示
(7)
式中:Aijkl—對(duì)稱張量;σij、σkl—應(yīng)力張量;KH—等效應(yīng)力。
對(duì)于其加工硬化現(xiàn)象及包辛格效應(yīng),可以應(yīng)用A-F非線性隨動(dòng)硬化模型[9]來(lái)表示,其方程式為
(8)

3.2 幾何模型
卷制螺旋彈簧的方法通常分2種[10],無(wú)芯軸時(shí)參數(shù)、形狀等可調(diào),有芯軸纏繞得到芯軸狀的彈簧,本文采用后者。方鋼與芯軸由咬緊裝置聯(lián)結(jié),使方鋼在芯軸的帶動(dòng)下被卷起并沿徑向移動(dòng)。
MSC.Marc是一款功能強(qiáng)大的有限元分析軟件,適用于彈簧卷制成形這類復(fù)雜的非線性問(wèn)題[11],彈簧的設(shè)計(jì)參數(shù)如表1所示。

表1 彈簧卷制過(guò)程需要的參數(shù)
根據(jù)表1中相關(guān)參數(shù)建立方鋼坯料的三維模型并采用相同的單元進(jìn)行網(wǎng)格劃分,共20000個(gè);同時(shí),建立芯軸、咬緊裝置、導(dǎo)向裝置和夾緊裝置的曲面模型,最終建立的有限元模型如圖8所示。
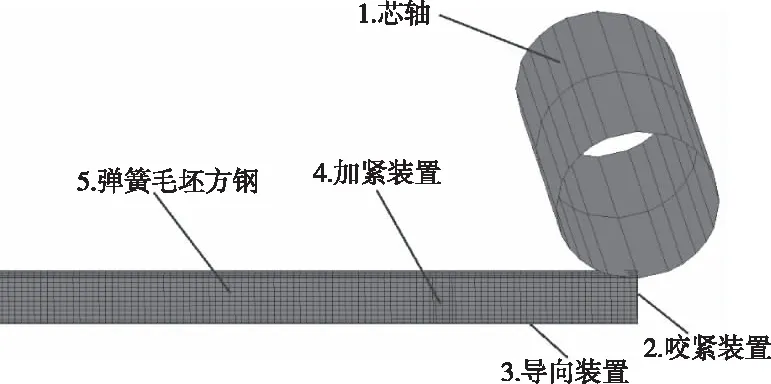
圖8 有限元模擬模型
3.3 模擬工藝參數(shù)設(shè)定
Q355鋼的質(zhì)量密度為7.85kg/m3,彈性模量為210000Mpa,泊松比為0.3。方鋼與芯軸、導(dǎo)向裝置、夾緊裝置之間的接觸方式均為Touching,與咬緊裝置之間的接觸方式為Glued。咬緊裝置與芯軸同時(shí)做水平移動(dòng)和轉(zhuǎn)動(dòng),并分別給予沿時(shí)間變化的速度曲線。方鋼在高溫?zé)峋砼c低溫冷卷時(shí)的卷制成形質(zhì)量有很大區(qū)別,因此初始溫度條件分為高溫下節(jié)點(diǎn)溫度為950℃,中溫為400℃,低溫為常溫25℃。單元類型選擇76號(hào)8節(jié)點(diǎn)六面體實(shí)體單元進(jìn)行分析計(jì)算。
3.4 無(wú)缺陷情況模擬結(jié)果
按照上述參數(shù)及要求進(jìn)行設(shè)置,提交計(jì)算得到后處理結(jié)果模型,彈簧卷制成功后的等效米塞斯應(yīng)力分布圖如圖9所示,從圖中可以看到其應(yīng)力計(jì)算結(jié)果符合產(chǎn)品要求,外形并沒(méi)有出現(xiàn)任何缺陷,可以作為成品彈簧。

圖9 彈簧卷制無(wú)缺陷的等效米塞斯應(yīng)力圖
4 數(shù)值模擬結(jié)果分析
經(jīng)過(guò)矩形截面彈簧成形極限圖曲線計(jì)算,f、w兩個(gè)成形質(zhì)量指標(biāo)的定義和有限元模擬計(jì)算,可以從MSC.Marc的結(jié)果處理文件中讀取到成形模擬計(jì)算結(jié)束后每個(gè)單元節(jié)點(diǎn)的最大主應(yīng)變以及最小主應(yīng)變的大小,然后在成形極限圖已知的條件下,完成f、w兩個(gè)指標(biāo)大小的計(jì)算。
4.1 加工階段單因素試驗(yàn)
4.1.1 速度對(duì)彈簧卷制質(zhì)量的影響
在矩形截面彈簧卷制成形的過(guò)程中,卷制速度是影響成形效率與成形質(zhì)量的重要因素,速度越快,卷制成品彈簧用時(shí)越少,因此需要兼顧成形質(zhì)量與成形效率以及時(shí)間成本。對(duì)于卷制速度分別取4r/min、2r/min和1r/min三個(gè)水平進(jìn)行仿真模擬。
將上述三組模擬成功的后處理結(jié)果中最大最小主應(yīng)變變化趨勢(shì)的數(shù)據(jù)導(dǎo)出,通過(guò)計(jì)算得到每個(gè)速度對(duì)應(yīng)的質(zhì)量指標(biāo)f和w的數(shù)值并記錄。兩個(gè)質(zhì)量指標(biāo)隨卷制速度變化的趨勢(shì)如圖10所示,可以看出,卷制速度越小,矩形截面彈簧成形的質(zhì)量越好,因此對(duì)于矩形截面彈簧的卷制,當(dāng)其它參數(shù)已經(jīng)確定或難以改變時(shí),可以通過(guò)減小速度來(lái)改善彈簧成形的質(zhì)量。

圖10 卷制速度對(duì)卷制質(zhì)量的影響
4.1.2 溫度對(duì)彈簧卷制質(zhì)量的影響
Q355鋼的塑性隨溫度的變化而變化且存在4個(gè)脆性區(qū)域[12],分別是超低溫度脆性區(qū)域(<-200℃)、藍(lán)脆區(qū)(200℃~400℃)、熱脆區(qū)(800℃~950℃)和高溫脆區(qū)(>1250℃),每個(gè)區(qū)域的最高溫屬于碳鋼塑性比較低的極端溫度,因此本文對(duì)于溫度參數(shù)選取常溫25℃、藍(lán)脆區(qū)400℃和熱脆區(qū)950℃三個(gè)數(shù)值進(jìn)行仿真模擬,同時(shí)高溫情況下的散熱問(wèn)題不予考慮。由于該三個(gè)溫度的塑性相對(duì)周圍溫度較弱,因此比各區(qū)內(nèi)其它溫度卷制的效果會(huì)更好,成形質(zhì)量也會(huì)更好。
采用與上節(jié)質(zhì)量指標(biāo)影響分析同樣的方法,得到它們隨溫度變化的趨勢(shì)如圖11所示。通過(guò)圖11可知:針對(duì)質(zhì)量指標(biāo)f來(lái)說(shuō),在高溫卷制時(shí),矩形截面彈簧的成形質(zhì)量?jī)?yōu)于在中低溫下卷制,指標(biāo)數(shù)值最小;而針對(duì)質(zhì)量指標(biāo)w來(lái)說(shuō),在常溫下卷制時(shí)的指標(biāo)數(shù)值最小,矩形截面彈簧的成形質(zhì)量?jī)?yōu)于在中高溫下卷制。這說(shuō)明在高溫下,碳鋼易發(fā)生起皺而不易被拉斷;而在低溫下,碳鋼易拉斷不易起皺。因此在矩形截面彈簧進(jìn)行卷制的過(guò)程中若經(jīng)常出現(xiàn)同一種缺陷,可以通過(guò)改變卷制溫度來(lái)克服。
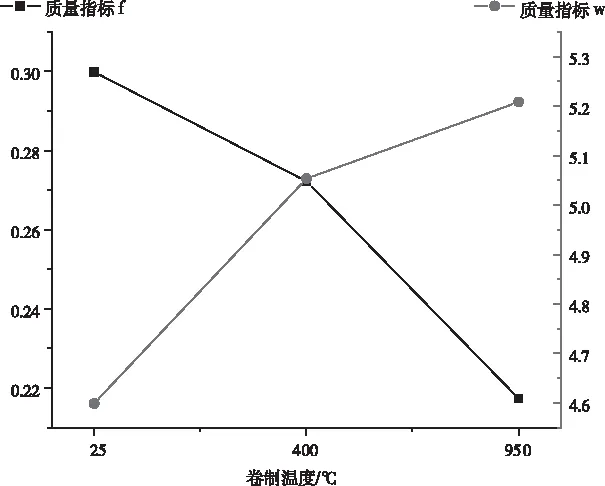
圖11 溫度對(duì)卷制質(zhì)量的影響
4.1.3 摩擦系數(shù)對(duì)彈簧卷制質(zhì)量的影響
影響因素摩擦系數(shù)指的是彈簧卷制用的芯軸與彈簧坯料方鋼之間的接觸摩擦系數(shù),而與方鋼與夾緊裝置和導(dǎo)向裝置的摩擦系數(shù)無(wú)關(guān)。由于本文選用的胚料及卷制設(shè)備芯軸的材料都是碳鋼,由機(jī)械設(shè)計(jì)手冊(cè)獲知,碳鋼的摩擦系數(shù)一般在0.1~0.3之間,因此對(duì)于影響因素摩擦系數(shù)來(lái)說(shuō),三個(gè)水平分別確定為0.1、0.2和0.3。然后分別將這三組數(shù)據(jù)進(jìn)行仿真模擬,得到不同摩擦系數(shù)下卷制成功的矩形截面彈簧的兩個(gè)質(zhì)量指標(biāo)變化趨勢(shì)如圖12所示。通過(guò)圖12可知:針對(duì)兩個(gè)質(zhì)量指標(biāo)來(lái)說(shuō),摩擦系數(shù)越大,指標(biāo)數(shù)值越小,卷制出彈簧質(zhì)量越好,既不易出現(xiàn)起皺缺陷也不易出現(xiàn)拉裂缺陷。
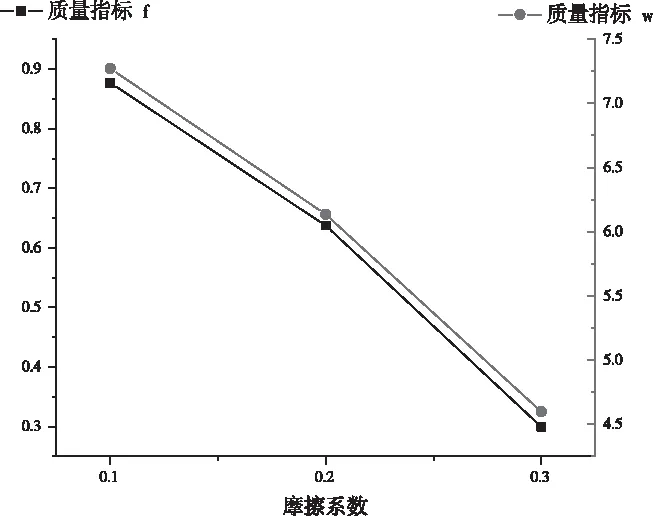
圖12 摩擦系數(shù)對(duì)卷制質(zhì)量的影響
4.2 加工階段參數(shù)正交試驗(yàn)
根據(jù)上一節(jié)中加工階段各個(gè)單一因素對(duì)矩形截面彈簧成形質(zhì)量的影響規(guī)律以及確定的每個(gè)因素的三個(gè)水平,匯總加工階段的影響因素水平表如表2所示,在該表的基礎(chǔ)上,建立影響因素、水平和質(zhì)量評(píng)價(jià)指標(biāo)的L9(33)正交試驗(yàn)表如表3所示。根據(jù)表3中數(shù)據(jù)建立9個(gè)有限元模型,通過(guò)計(jì)算得到質(zhì)量評(píng)價(jià)指標(biāo)等數(shù)據(jù),再計(jì)算均值大小k和極差R來(lái)判斷各影響因素對(duì)卷制質(zhì)量的影響大小。
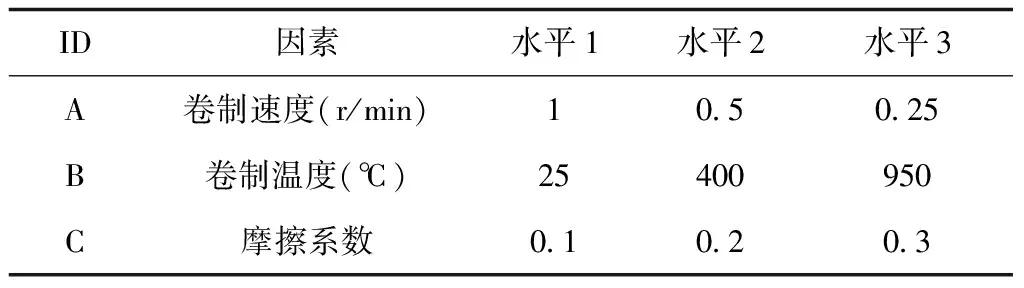
表2 正交試驗(yàn)加工階段影響因素水平表

表3 加工階段影響因素、水平、質(zhì)量評(píng)價(jià)指標(biāo)的L9(33)正交試驗(yàn)表
針對(duì)質(zhì)量指標(biāo)f,影響因素卷制速度的均值中kf3最小,因此卷制速度為0.25r/min時(shí)是三個(gè)水平中的最優(yōu)水平。同樣可以得出卷制溫度為高溫950℃為溫度的三個(gè)水平中的最優(yōu),摩擦系數(shù)為0.3時(shí)為影響因素摩擦系數(shù)中三個(gè)水平中的最優(yōu)。因此最優(yōu)組合為速度0.25r/min,摩擦系數(shù)0.3在高溫950℃下彈簧卷制質(zhì)量?jī)?yōu)。針對(duì)質(zhì)量指標(biāo)w,影響因素卷制速度與摩擦系數(shù)同質(zhì)量指標(biāo)f一樣都是在速度為0.25r/min和摩擦系數(shù)為0.3時(shí)最優(yōu),不同之處在于卷制溫度在常溫25℃時(shí)kw1較其它極差小,因此對(duì)于起皺指標(biāo)在常溫下卷制時(shí)更優(yōu)。因此最優(yōu)組合為速度0.25r/min,摩擦系數(shù)0.3在常溫25℃下彈簧卷制質(zhì)量?jī)?yōu)。想要進(jìn)一步得到綜合f與w的最優(yōu)組合,還需進(jìn)行其它相關(guān)試驗(yàn)進(jìn)行分析。
比較正交表中極差R的大小來(lái)確定不同影響因素對(duì)成形質(zhì)量影響的程度;兩個(gè)質(zhì)量指標(biāo)具有相同的大小順序,都是R摩擦系數(shù)>R溫度>R速度,因此可以得出結(jié)論是摩擦系數(shù)變化對(duì)矩形截面彈簧卷制成形質(zhì)量的影響最大,卷制速度大小的變化對(duì)其質(zhì)量的影響最小。
5 結(jié)論
1)基于成形極限圖所制定的質(zhì)量評(píng)價(jià)準(zhǔn)則可以有效地對(duì)矩形截面彈簧成形進(jìn)行質(zhì)量評(píng)價(jià),判斷是否可能發(fā)生拉裂和起皺缺陷。
2)當(dāng)矩形截面彈簧尺寸一定,加工階段的三個(gè)影響因素中,卷制速度越小,卷制成形成功率越高;摩擦系數(shù)在0.1~0.3的范圍內(nèi)越大,彈簧卷制成形的質(zhì)量越好,拉裂和起皺缺陷均不易出現(xiàn);而對(duì)于溫度則顯示,高溫下Q355板材易發(fā)生起皺而不易被拉斷,低溫下,碳鋼易拉斷不易起皺。
3)通過(guò)正交試驗(yàn)得到,材料摩擦系數(shù)對(duì)矩形截面彈簧卷制成形質(zhì)量的影響最顯著,其次是溫度和速度;對(duì)于拉裂缺陷,在加工階段的影響因素的三個(gè)水平中的最優(yōu)組合為0.25r/min的速度、0.3的摩擦系數(shù)以及950℃的高溫;對(duì)于起皺缺陷,以速度0.25r/min、摩擦系數(shù)0.3在常溫25℃下彈簧卷制質(zhì)量為最優(yōu)。上述工藝參數(shù)經(jīng)實(shí)際加工試用,試件成形質(zhì)量符合預(yù)期規(guī)律。

