模型預測控制在軌道交通虛擬耦合列控系統中的應用

張小林 趙 磊

(上海富欣智能交通控制有限公司，201203，上?！蔚谝蛔髡?，高級工程師)

隨著人們出行需求的提高以及城市群的興起，如何提高軌道交通線路通過能力已成為需要解決的問題。在不改變線路和增加車輛配置的基礎上，通過研究和部署新型列控系統以提高運輸能力已成為解決這一問題的重要手段。

隨著自動駕駛、物聯網以及5G通信等技術的發展，近年來對于虛擬耦合列控技術［1-2］的研究成為熱點。不同于既有列控系統，虛擬耦合列控系統借助車-車間的直接通信，不再將前行列車視為靜止，而是將同一方向上前后多列車虛擬耦合成1列列車進行協同控制，從而達到縮短運行間隔、提高線路通過能力的目的。

本文將在介紹虛擬耦合列控技術基礎上，對協同編組這一關鍵實現技術進行分析及建模仿真。

1 虛擬耦合列控系統

虛擬耦合列控系統(見圖1)借助先進的無線通信、傳感和控制等技術，從地面獲得軌旁設備狀態及控制指令，并基于車間通信從相鄰列車獲得列車位置、速度、加速度等關鍵信息，形成輸入信息協同控制相鄰列車間的運行速度和間隔距離，形成1個穩定車隊整體在統一的移動授權防護下運行，共同完成列車控制與調度組織。列車的間隔距離不再是基于前車靜止而是基于兩車相對速度和位置，可實現更高效率的基于相對速度的列車控制。

圖1 虛擬耦合列控系統簡圖Fig.1 Schematic diagram of virtual coupling train control system

相較于現有列控技術，虛擬耦合列控系統的關鍵優勢在于多列列車之間的虛擬編組和協同控制，因此應重點研究相關協同控制理論和技術方法。該理論和技術方法的研究成為了新型列控系統能否取得實際運用的關鍵因素。

2 多智能體協同編組技術

將單列列車視為智能體，多列列車的系統編組實際上是1個多智能體(MAS)系統控制編組［3］問題。MAS的編組控制是指在選取合適的控制策略的前提下，統一協調控制MAS中各個智能體的運動，使有多個同類或者相似智能體組成的系統從任意初始條件出發，都能夠達到預期相對位置，并能夠維持系統隊形不變，同時溝通合作，以完成特定任務的控制過程。

目前，隊形控制已廣泛在航天器群體、機器人群體［4］、GPS(全球定位系統)車隊及艦隊等的協同作業中。用于MAS編隊控制的主要控制方法有基于行為的控制方法、基于虛擬結構的控制方法、領導者-追隨者控制方法、模型預測控制(MPC)方法，以及基于廣義坐標的控制方法等。其中，MPC方法［5-6］因建模簡單、控制靈活、具有在線優化能力，以及魯棒性強等特點得到了廣泛應用。本文將基于MPC方法對列車虛擬編組和系統控制進行建模和仿真。

3 MPC建模

3.1 MPC原理

作為一種控制方法，MPC法主要包含預測模型、滾動優化和反饋校正3個基本要素，分別對應利用空間狀態方程預測系統未來狀態、基于目標函數在線求解優化、將求解的最優值作用于系統控制這3個過程。MPC法的作用機理可描述為:在每個采樣時刻，根據獲得的當前信息，在線求解1個有限時間優化問題，并將得到的控制序列的第1個元素作用于被控對象;在下個采樣時刻，重復上述過程，用新的測量值作為此時預測系統未來動態的初始條件，重新求解。

3.2 列車縱向運動學模型

列車的縱向運動過程可由以下微分方程描述:

式中:

s——列車相對于參考點的縱向距離;

v——列車的速度;

a——列車的加速度。

式中:

c——控制輸入;

f(v，a)——列車阻力方程;

b(v)——列車牽引、制動控制輸入滯后方程。

式(2)可用以下列車加速度方程描述:

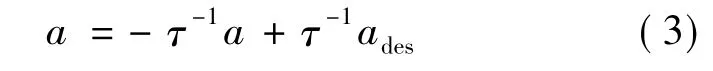
式中:

ades——列車控制器所決定的期望加速度;

τ——時間常數。式(3)表明，列車加速和減速控制特性可用一階滯后建模，即實際加速度a以τ跟蹤ades。

3.3 狀態空間模型

考慮同一軌道上有多列列車運行，基于協同控制的列車跟蹤示意圖如圖2所示。

圖2 基于協同控制的列車跟蹤示意圖Fig.2 Schematic diagram of train tracking effect based on MPC

圖2中，es計算如下:

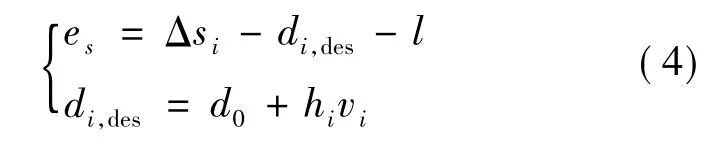
式中:

d0——靜止時列車間最小安全距離;

hi——常數。

此外，定義前、后列車的速度差為:

根據式(2)、式(4)—式(7)，可以推導出列車狀態空間模型為:

其中:

式中:

x、u、ω——分別為狀態矢量、控制輸入及干擾。

在此模型中將前車加速度視為干擾。

3.4 離散化和模型預測

根據以上狀態空間模型，進行離散化可得:

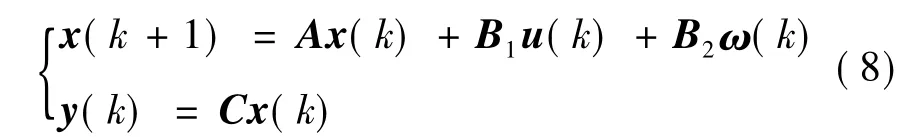
式中:

x(k)——第k周期系統狀態向量;

y(k)——系統輸出;

u(k)——系統控制輸入;

ω(k)——前車加速度;

C——輸出矩陣。

若T為系統周期，I為單位矩陣，則:

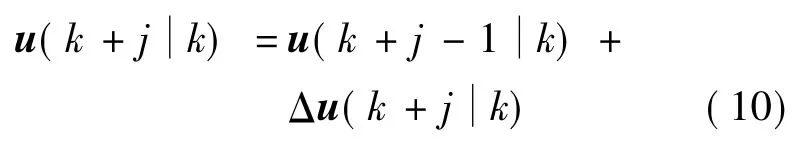
則增量控制形式的模型預測狀態方程為:

其中:

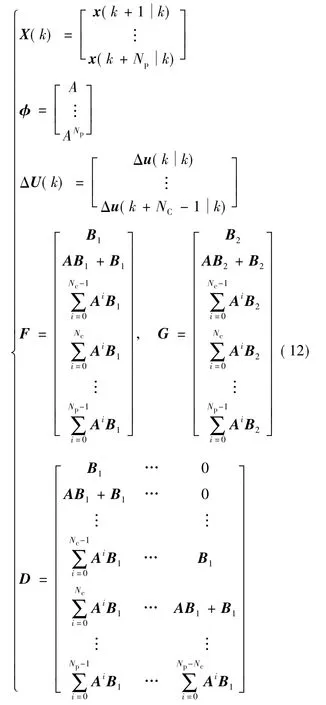
式(12)中，Np為預測時域，Nc為控制時域，并應滿足Nc≤Np。

則k時刻的預測控制輸出為:

3.5 控制優化

首先，定義性能指標函數:

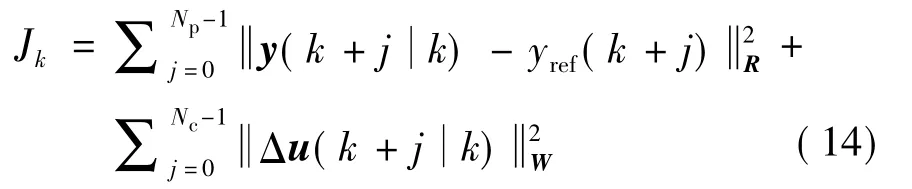
式中:

yref——參考值;

R——誤差加權矩陣;

W——輸入加權矩陣。

可以向量形式將式(14)表示為:

式中:

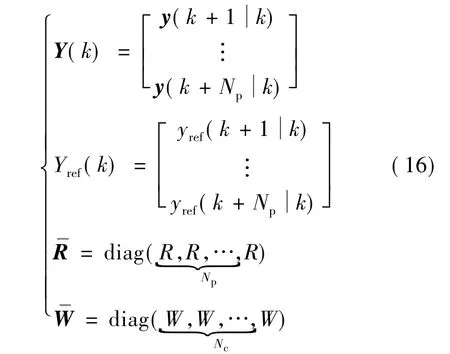
定義向量E(k)為系統自由響應與未來目標參考值的偏差，則:

其中:

將式(17)代入式(15)可得:

其中:

式(19)可被寫為二次規劃的標準形式:

其中:

由于Δu(k)是極小化性能指標得到的解，則必須滿足極值必要條件:

根據式(2)可得ΔU(k)的解為:

至此，以Δu(k)作為k時刻的增量控制輸入即可。

4 MPC仿真

為驗證MPC的有效性，模擬3列列車跟蹤運行，第1列列車(頭車)加速度以一定周期進行上下波動。通過仿真來觀察第2列和第3列列車追蹤頭車的運行情況。模擬軟件采用Python語言編程，T為100 ms，Np和Nc分別為10和6，τ和hi均為1。圖3為3列列車仿真速度曲線圖。

根據圖3，第2列列車和第3列列車的初始速度均為10 m/s，在非穩態時，第2列列車和第3列列車根據與第1列列車的速度差和距離差進行快速調整;在進入穩態后，跟隨第1列列車速度進行速度調整。從圖3的局部放大圖可以看出，在第1列列車速度周期性變化階段，第2列列車和第3列列車可以快速進行速度調整，并跟蹤前車速度變化達到穩定運行狀態。

圖3 基于MPC的列車跟蹤效果仿真速度曲線圖Fig.3 Simulation speed curve of train tracking effect based on MPC

圖4為3列列車追蹤運行位置間隔仿真圖。由圖4可以看到，3列列車按照等間隔運行，間隔距離保持不變;在第1列列車速度周期性變化時，后車可以很好地跟蹤前車并保持恒定間距。

圖4 基于MPC的3列列車跟蹤運行位置間隔仿真圖Fig.4 Simulation diagram of position interval of threevehicle tracking running based on MPC

5 結語

本文根據一種基于MPC理論的協同算法，將其應用到虛擬耦合列控系統協同編組追蹤運行場景中。利用Python語言編寫MPC，對3列列車跟蹤進行模擬仿真，頭車速度在一定頻率周期性變化條件下，后車能追蹤前車并保持與前車一定的間距;后車速度跟隨前車速度變化，與前車速度保持一致，可保持隊形的穩定。根據以上模擬仿真，本算法可以很好地應用到軌道交通列車追蹤運行場景中，可有效解決在其他列車投入運行或有列車退出運行后，使列車車隊處于不穩定態時，能迅速進入等間隔、同速度的運行穩定態問題。

后續研究將會考慮列車運行性能和線路運行條件等因素對本方法的影響，優化該方法以便更符合軌道交通列控系統的復雜要求。